正交并联六维力传感器结构性能及参数优化
2018-06-04王志军
李 化,王志军,贺 静
(1.华北理工大学 机械工程学院,河北 唐山 063210;2.河北省工业机器人产业技术研究院,河北 唐山 063210;3.唐山工业职业技术学院,河北 唐山 063299)
0 引言
六维力传感器因其具有同时感知并测量外力和外力矩的优点[1],被广泛应用于航空航天、工业生产等领域[2]。在众多传感器中,Stewart并联六维力传感器因其具有刚度大、承载能力强、无误差积累等优点[3],成为越来越多研究者的研究对象。赵延治等人提出了一种全压向力弱耦合自标定并联六维力传感器结构,为自标定型传感器奠定了基础[4];王志军等人提出了一种新型的并联预紧式双层结构六维力传感器,并建立其数学模型,对并联预紧式六维力传感器的研究与开发提供了参考[5]。
结构参数优化是指对任务模型的结构参数进行调整,使其能够适应特定的工作情况,对传感器精度和实用性具有重要意义,为实际传感器结构设计提供了重要参考。姚建涛和高峰分别从数学解析和性能图谱方面分析了各向同性,优化了传感器结构参数[6-7];佟志忠等人提出了考虑测量末端为解耦中心的结构参数优化方法,为该类传感器的研究提供了新的思路[8]。但是多数情况下,机器人工作环境是复杂的,此时,各向同性性能指标不是最优的。因此,基于实际工况进行传感器结构参数优化并确定传感器的量程,更具有实际工程意义。王航等人提出基于任务模型的传感器性能优劣评价指标,为并联结构传感器在实际应用中的结构设计奠定了基础[9]。本文提出一种六分支正交并联六维力传感器,即水平测量分支与竖直测量分支正交排布,推导出其受到六维外力时,测量分支作用反力的映射矩阵,并基于工况函数,以减小传感器测量分支量程且结构稳定为优化目标,提出一种基于实际工况函数的结构参数优化方法,该方法以满足工况函数为前提,确保了优化结果的可行性。最后,以打磨卫生陶瓷曲面为实例验证了该优化方法的优越性。
1 六分支正交并联六维力传感器测量原理
1.1 传感器结构分析
图1为六分支正交并联六维力传感器的结构示意图。该传感器由测力平台b1b2b3、固定平台B1B2B3(两平台结构相同,半径为a1,两平台之间距离为L)和6个测量分支(b1B1、b2B2、b3B3为3个竖直分布的测量分支,铰点呈等边三角形分布,b4B4、b5B5、b6B6为3个水平分布的测量分支, 均相切于半径为a2的圆,切点为水平测量分支中点)组成,坐标系o-xyz为传感器的测量基准坐标系,原点选择为测力平台几何中心,测力平台与水平测量分支之间的距离为a3。
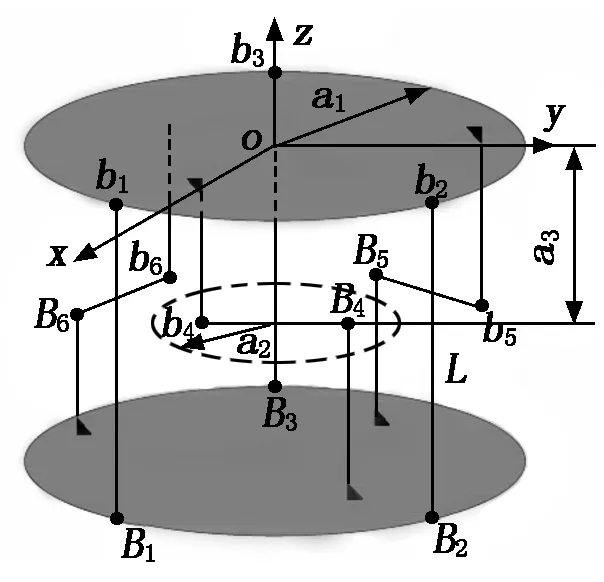
图1 正交并联六维力传感器结构示意图
1.2 传感器静力学分析
以螺旋理论为基础,六分支并联六维力传感器测力平台静力学平衡方程为:
Fw=Gf.
(1)
其中:Fw为作用在测力平台上的空间三维外力或空间三维外力矩矢量;G为6个测量分支所受轴向力与六维外力之间的映射系数矩阵;f为6个测量分支轴向力矢量。
6个测量分支所受轴向力与六维外力之间的映射系数矩阵为:
(2)
Bp=[a1cosζpa1sinζp-L]Tp=1,2,3.
(3)

(4)
bp=[a1cosζpa1sinζp0]Tp=1,2,3.
(5)

(6)

在式(1)两侧同时乘以G-1得:
f=G-1Fw.
(7)
式(7)为六维外力与测量分支反作用力之间的关系 。
经计算得:

(8)
式(8)为测力平台在六维力作用下与测量分支作用反力的映射关系。由式(8)可看出,影响结构参数的只有a1、a2和a3,与各维列向量均不相关,即此时传感器不处于奇异位形,则六维力可由分支轴向力唯一确定。
2 传感器优化准则
根据以上的理论分析可知,传感器在受到外力时,如果每个测量分支只会受到沿轴线方向的拉力或者压力时,通过分析传感器每一个测量分支的受力情况就可以分析整体的受力。
本文以六分支正交并联六维力传感器为模型,当其满足工况函数模型时,以减小测量分支量程为目标对其进行结构优化。
设机器人完成一个工作周期的时间为T,在周期T内,由外力作用产生的轴向反作用力的函数表达式f(t)为:
f(t)=G-1Fw(t)=[f(t1)f(t2)…f(tn)].
(9)
其中:f(tj)为tj时刻测量分支在施加外力时产生的轴向反作用力,j=1,2,…,n。
第i个测量分支所受的轴向反作用力为fi(t),表示为G的第i行与Fw(t)的代数和,由此易知,Fw(t)在时间周期T∈(0,t)内有定义且有界,因此fi(t)为有界函数,即在时间周期T∈(0,t)内,fi(t)一定存在最小值和最大值。鉴于六维力传感器的测量分支受到沿轴向正、反两方向的力及绕轴向正、反两方向的力矩,因此以测量分支轴向反作用力fi(t)的绝对值为优化目标,优化步骤如下:
(1) 计算测量分支受力最小。在时间周期T∈(0,t)内,存在:
fmin(t)≤|fi(t)|≤fmax(t)i=1,2,…,6.
(10)
其中:fmin(t)和fmax(t)分别为函数|fi(t)|的最小值和最大值。
第i个测量分支由外力引起的最大轴向反作用力为:
(11)
其中:Fxm、Fym、Fzm分别为空间外力x、y、z方向的最大值;Mxm、Mym、Mzm分别为空间外力矩x、y、z方向的最大值。
当测量分支量程轴向力的最大值趋于最小时,满足传感器的参数优化,即在满足工况函数的前提下,fi max(tj)最小,测量分支量程则最小。求解的具体方法如下:求出每一个测量分支的最大轴向力,对其取绝对值,fA为6个测量分支最大轴向力中的最大值,即fA为fmin中最大的一项;搜索fA,当fA取得最小时对应的结构参数即为优化目标,即在满足工况函数的前提下,测量分支的最大轴向力最小。经优化得到的传感器在工况函数下测量分支量程最小,传感器尺寸最小。
(2) 计算测量分支受力的方差最小。设σ为轴向反作用力f每一列的标准差,每一列的最大值为σB,搜索σB中的最小值,该最小值即为所对应的结构参数的优化目标,即在工况函数下,测量分支轴向力趋于一个稳定值,此时,传感器各测量分支受力均衡,稳定性好。
在满足以上优化方法时,工况函数下传感器既满足了测量分支量程较小,也使传感器结构稳定,传感器结构达到了最优。基于工况函数的结构参数优化,对设计并联结构六维力传感器更具有应用价值。
3 六分支正交并联六维力传感器结构参数优化
本文以六自由度通用机器人进行卫生陶瓷曲面打磨作业为例,对具体的工况函数进行优化。
通用机器人卫生陶瓷曲面打磨作业具体工况如下:工作周期T=23 s,打磨步骤为吹尘(0≤t<17)-打磨外部曲面(17≤t<17.5)-打磨内部曲面(17.5≤t<22.5)-细致打磨不便打磨的地方(22.5≤t<23)。
根据卫生陶瓷曲面打磨的经验,可得到具体的空间接触外力函数Fx(t)、Fy(t)、Fz(t)(N)和空间接触外力矩函数Mx(t)、My(t)、Mz(t)(N/mm)表达式:
(12)
(13)
(14)
(15)
(16)
Mz(t)=0 0≤t<23.
(17)
式(12)至式(17)确定了卫生陶瓷在曲面打磨作业中受到的空间六维外力的工况函数Fw(t)。正交并联六维力传感器安装在六自由度机器人手臂末端,检测六维力Fw(t)在曲面打磨过程的变化。
由式(8)可以看出,六分支正交并联六维力传感器只有a1、a2、a3三个结构参数,为简化计算,假设a3=15 mm,仅分析分支最大轴向力与结构参数a1、a2的关系即可。
给定结构参数a1和a2的区间[40,70]和[20,50] 以及步长向量λ=[1 1]。在a1和a2的区间内,根据已给定的步长λ逐一给映射关系矩阵G-1中的a1和a2赋值,再经计算,整理得到式(9)和式(10)的具体表达,利用MATLAB分别进行数值计算获得最终结果,如图2、图3所示。
由图2、图3可知:当传感器满足测量分支量程最小时,结构参a1=70 mm,a2=20 mm;当传感器满足结构最稳定时,a1=70 mm,a2=28 mm。
由图2可以看出,在自变量范围内fA递减;由图3可以看出,在自变量a2∈(20,30)内,σB递减。因此同时满足两种优化结果时,取a1=(70+70)/2=70 mm,a2=(20+28)=24 mm。

图2 测量分支受力最小优化结果 图3 测量分支受力方差最小优化结果
4 结论
本文提出一种六分支正交并联六维力传感器,通过螺旋理论建立了其静力学平衡方程,得到了测力平台在六维力作用下向测量分支反作用力的映射关系。根据传感器的受力情况,提出了一种基于工况函数的优化准则,最后以六分支正交并联六维力传感器为例,针对机器人曲面打磨作业进行结构优化,验证了该优化方法的可行性。
参考文献:
[1] 赵克转,徐泽宇.一种新型工业机器人六维力传感器设计研究[J].传感器与微系统,2015,34(5):5-7.
[2] Dwarakanath T A,Bhutani G.Beam type hexapod structure based six component force-torque sensor[J].Mechatronics, 2011, 21: 1279-1287.
[3] 姚建涛,崔朋肖,朱佳龙,等.预紧式并联六维力传感器容错测量机理与标定测试研究[J].机械工程学报,2016,52(8):58-66.
[4] 赵延治,焦雷浩,牛智,等.机械解耦自标定并联六维力传感器设计及仿真[J].中国机械工程,2017,28(7):771-778.
[5] 王志军,姚建涛,王航,等.并联预紧式六维力传感器动态力响应分析[J].机器人,2011,33(4):455-460.
[6] 姚建涛.大量程并联式六维力传感器基础理论与实验研究[D].秦皇岛:燕山大学,2010:100-102.
[7] 王洪瑞,陈贵林,高峰,等.基于Stewart平台的六维力传感器各向同性的进一步分析[J].机械工程学报,2000,36(4):49-52.
[8] 佟志忠,姜洪洲,何景峰,等.基于单叶双曲面的标准Stewart并联结构六维力传感器各向同性优化设计[J].航空学报,2011,32(12):2327-2334.
[9] 王航,姚建涛,侯雨雷,等.面向任务的并联结构六维力传感器设计[J].机械工程学报,2011,47(11):7-13.
