风雨耦合作用下桥梁主梁涡振节段模型试验

雷 旭，陈政清，华旭刚，黄智文，聂 铭，肖 凯

(1. 广东电网有限责任公司电力科学研究院，广东 广州 510080； 2. 湖南大学 风工程试验研究中心，湖南 长沙 410082)

0引 言

涡激振动是大跨度桥梁在低风速下容易发生的风致限幅振动现象[1-2]，尽管不同于颤振和驰振那样的发散性振动，但因发生频次高并且振幅较大，其同样会影响行车安全和结构耐久性。值得注意的是，目前的研究大多集中于纯风作用下的主梁涡振，而在现实环境下，风和雨往往耦合在一起对结构产生作用，针对风雨耦合作用时的此类研究却极为缺乏，相关结论[3-5]还需加以验证。

风雨对结构作用的分析涉及气-液-固三相耦合，较难模拟和理论分析，故目前最可靠的研究方法是风洞试验。要保证风雨耦合试验结论的正确性，关键是确立雨强相似比。关于这一相似比的建立，相关研究正在开展，Bilanin等[6-7]为研究降雨对飞机失速的影响，在假设雨滴大小和间隙可调的前提下依据含水量不变的原则，利用量纲分析法得到了理论雨强相似关系，但实际降雨设备不能实现这种相似比。Surry等[8-9]依据雨滴形态、雨滴速度与雨滴运动的Froude数一致原则推导出考虑建筑物迎风面荷载时的雨滴密度相似比为1∶1，但桥梁主梁不能仅考虑迎风面阻力，故此相似关系不适用于主梁结构。

综上所述可知，在目前的试验条件下，还没有形成针对桥梁主梁的风雨试验雨强相似关系。基于此，本文首先依据降雨特性和结构模型试验相似理论推导了原型和模型雨强相似比，然后在实验室实现了4类典型主梁断面在不同雨强下的模型动力特性和涡振响应试验。通过推导的雨强相似关系和试验结果分析了降雨对主梁涡振的影响规律，以期能为实现大跨度桥梁抗风的精细化研究提供参考。

1降雨对结构作用的理论分析

1.1降雨基本特征

目前一般认为自然界雨滴为球形且雨滴谱服从M-P分布[10]，由此可得单位体积内直径为D的雨滴数N(D)为

N(D)=N0e-λD

(1)

式中：N0为浓度参数，N0=8 000；λ为尺度参数，λ=4.1I-0.21，I为竖向雨强。

单位体积空气含水量WL表示为

(2)

式中：ρr为水的密度。

直径D的雨滴下落的竖向速度和水平速度可以按下式计算[11]

vr(D)=9.58[1-exp(-(D/1.77)1.147)]

(3)

ur(D)=κU

(4)

式中：vr(D)，ur(D)分别为雨滴的竖向速度和水平速度；U为结构物处水平风速；κ为雨滴水平速度修正系数[12]。

降雨对结构的作用体现在改变空气密度、对结构的冲击以及引起结构表面积水3个方面，如图1所示。已有文献计算结果[5,13]表明，雨强达到1 000 mm·h-1时，空气密度增大量仅为2%，其基本可以忽略。

1.2雨滴冲击作用

以图2(a)中矩形主梁断面为例，其顶面和侧面分别用Ⅰ区和Ⅱ区表示。将雨滴直径用等效直径D0表示，并假设雨滴数密度为n0，雨滴水平速度和竖直速度分别为ur0和vr0，可得风雨耦合对主梁的作用如图2(b)所示。

由图2(b)可知，时间τ内落在顶面Ⅰ区和侧面Ⅱ区直径为D0的雨滴数N为

N=(LHur0+LBvr0)τn0

(5)

式中：L，B，H分别为矩形的长、宽、高。

雨滴的竖向动量Prv为

(6)

将式(6)中的vr0用水平速度ur0替代即可得水平动量Pru。依据动量定理可知，时间τ内，落在Ⅰ区和Ⅱ区的雨滴动量为平均冲击力的冲量，对竖向冲击，其可用下式表示

(LHur0+LBvr0)WLτvr0

(7)

式中：Frv为时间τ内雨滴平均竖向冲击力。

将式(7)两边消去τ，则可得Frv的表达式，即

Frv=(LHur0+LBvr0)WLvr0

(8)

式(8)中将括号外的竖向速度vr0用水平速度ur0替代即可获得相应的平均水平冲击力Fru表达式。

1.3表面积水厚度

结构表面的浅层径流受雨强、坡面长度和坡度、雨滴打击、结构粗糙度等因素影响，难以估算准确。对于主梁，若不考虑其附属构件对水流的阻碍，可作为单宽一维自由排水截面[14]，坡度不变，沿长度方向排水状态一致且水流从坡角无阻碍自由流出，见图3(a)。因水的表面张力有限，积水厚度存在极限，如图3(b)所示[15]。

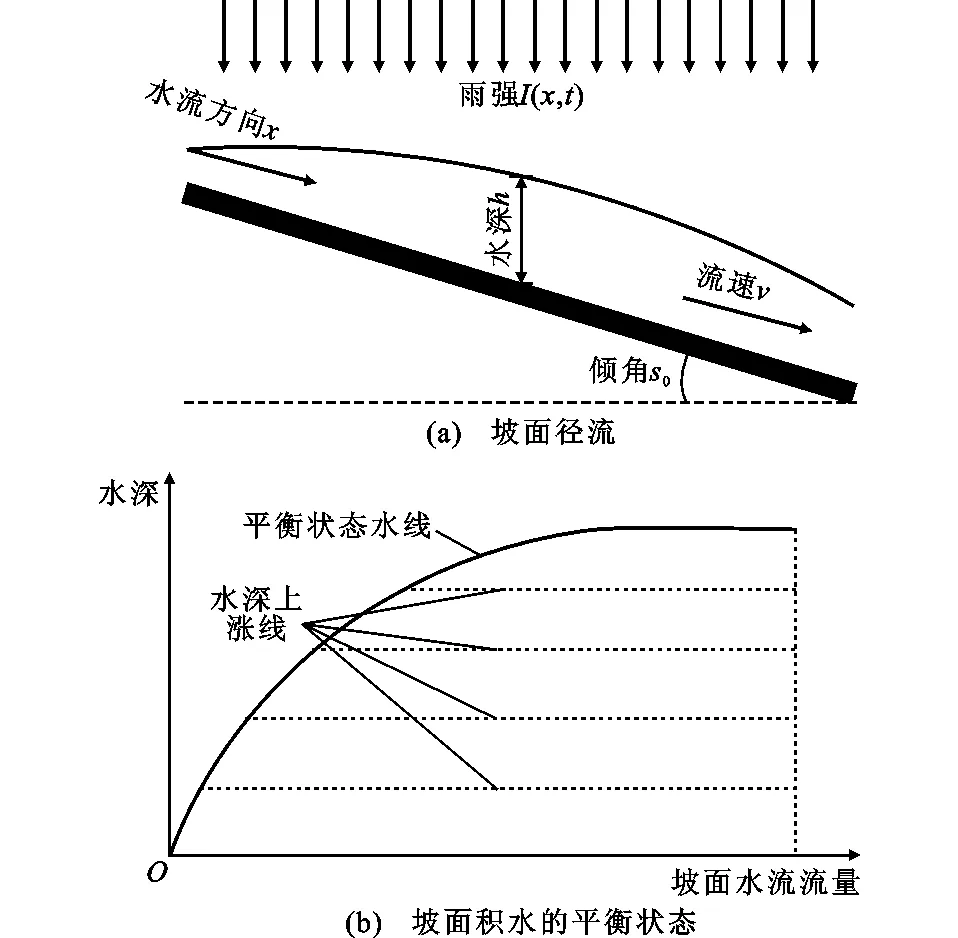
季天剑[14]通过试验和回归分析得到了与实际吻合较好的单宽一维自由排水路面积水厚度经验公式，即

(9)

式中：Hr，Ls，S，TD分别为水膜厚度、坡面长度、坡度和坡面构造深度，对于公路路面TD一般可取为0.1 mm。

由式(9)计算后可知：雨强为1 000 mm·h-1且排水长度为50 m时，水膜厚度仅为10 mm左右，相比3～4 m的主梁高度，其只占到0.33%的比例，因此，除非桥面壅水严重，一般可不考虑雨膜对主梁外形的影响。

2雨强相似关系的建立

2.1模型试验相似基本理论

由相似的定义可知：2个系统完全相似，则互相对应的任意一对量纲一的物理量必须相等，其可表示为[15]

(10)

式中：f1，f2分别为第1和第2系统物理量；F1，F2分别为第1和第2系统特征值；量纲一的物理量为第1和第2系统物理量与对应特征值的比值。

对某一复杂的物理现象，式(10)指代的相似准则数目较多，而且有可能互相矛盾，要实现完全相似几乎不可能，对于具体问题，可根据研究需要选取主要准则，实现部分相似。

2.2考虑雨滴冲击的雨强相似关系

由公式(8)可知竖向和水平雨滴冲击力Frv，Fru可表示为[15]

(11)

式中：n为直径D的雨滴数密度。

由模型和原型的顺风向风荷载和雨滴水平冲击力量纲一的比值一致原则，可以建立如下的相似关系[15]

(12)

式中：下标m,p分别表示模型和原型值，下同；CD为风轴坐标系下的主梁截面阻力系数，其在模型和原型中保持一致；ρa为空气密度。

公式(12)化简后可得仅考虑雨滴冲击的顺风向雨强相似比方程，即

(13)

式中：λU，λH，λn，λD分别为水平风速、断面高度、雨滴数密度以及雨滴粒径的模型与原型相似比；λHur+Bvr为运算式Hur+Bvr的模型与原型相似比。

同理可得竖向雨强相似比方程，即

(14)

式中：λB，λvr分别为断面宽度、雨滴竖向速度的模型与原型相似比。

将公式(13)，(14)联立，并由几何相似比一致(λB=λH)可得同时满足顺风向和竖向相似关系的雨强相似准则为

(15)

由于雨滴竖向速度难以人工调节，因此难以满足公式(15)中的λU=λvr，但喷雨装置可以使喷出雨滴的粒径形态、竖向终点速度和自然界基本一致，即λD=1，λvr=1，据此，公式(15)的相似关系可以被简化，特别是针对大跨度主梁截面，宽高比B/H较大，且振动以竖向为主，因此可以只考虑降雨的竖向冲击，而不计算其侧面的受力，即假设H=0。由以上假设并依据式(14)可得主梁风雨耦合作用试验的简化相似关系，即

(16)

根据雨强I与WL的关系式(2)，可得

(17)

式中：i表示雨滴粒径类型，总共计算j种粒径类型；Di，ni分别为对应雨滴直径和密度；a，b均为常数，取值分别为0.089和0.846。

最后可将式(16)变换为如下形式

(18)

式中：λI为模型与原型的雨强相似比。

2.3考虑表面积水的雨强相似关系

表面积水会产生附加的竖向作用力，若三分力规定为风轴坐标系下的相应值，则会产生附加升力和扭矩，从而对结构的风致静动力响应带来相应影响。另外，某些结构动力特性较易受质量和气动外形的影响，也需建立由积水质量和外形给出的雨强相似关系。

2.3.1基于结构风致三分力与雨致三分力之比一致的雨强相似关系

风轴坐标系下，考虑表面积水的主梁竖弯振动气动升力和扭矩相似关系为

(19)

式中：FL，FrL分别表示风致和雨致静气动升力；MTθ，MrTθ分别表示风致和雨致静气动扭矩。

由于扭矩相似比由升力决定，故式(19)可只计算第一分式，其可表示为

(20)

式中：CL为主梁升力系数；g为重力加速度。

变换式(20)后得水膜厚度的相似比λHr为

(21)

同样，根据水膜厚度经验公式(9)可得到如下的雨强相似关系，即

(22)

式中：λL,λTD分别为排水坡长、坡面构造深度的模型与原型相似比。

2.3.2基于结构质量(尺寸)与积水质量(尺寸)之比一致的雨强相似关系

考虑结构和积水质量比值不变的原则，也可建立如下相似关系，即

(23)

式中：ρs为结构物密度。

由结构物质量密度的相似比λps=1∶1，并依据前述水膜厚度计算公式(9)，可由式(23)变换得到雨强相似比，即

(24)

同样，考虑主梁和积水厚度比值不变时的雨强相似比也可用式(24)表示。

2.4雨强相似关系的选取

对于频率测试等只与质量相关的试验，可只考虑相似关系式(24)，无风时的机械阻尼特性试验雨强相似比可取为1∶1。对于涡振和颤振等主梁动力响应试验，由于积水尺寸和质量相比主梁高度和质量一般可忽略，故可只考虑相似关系式(18)。

3风雨耦合作用下涡振节段模型试验

3.1试验工况

试验在湖南大学HD-2风洞中的风雨试验段进行，该试验段风速超过2 m·s-1后，湍流度小于2%，风场品质良好。降雨装置采用QYJY-501型人工模拟降雨器，其雨滴粒径和终速与天然降雨接近。

节段模型和传感器布置方式如图5所示，因存在顺风向限位钢丝，只考虑竖向和扭转振动。试验模型选取了4类典型的桥梁主梁截面，如图6所示，模型长度均为1 540 mm，截面横坡坡度为2%。模型和原型的相似关系以及试验工况如表1所示。因不同试验攻角下的规律基本一致，仅给出0°攻角试验结果，并据此予以分析，获得降雨对结构振动的影响规律。

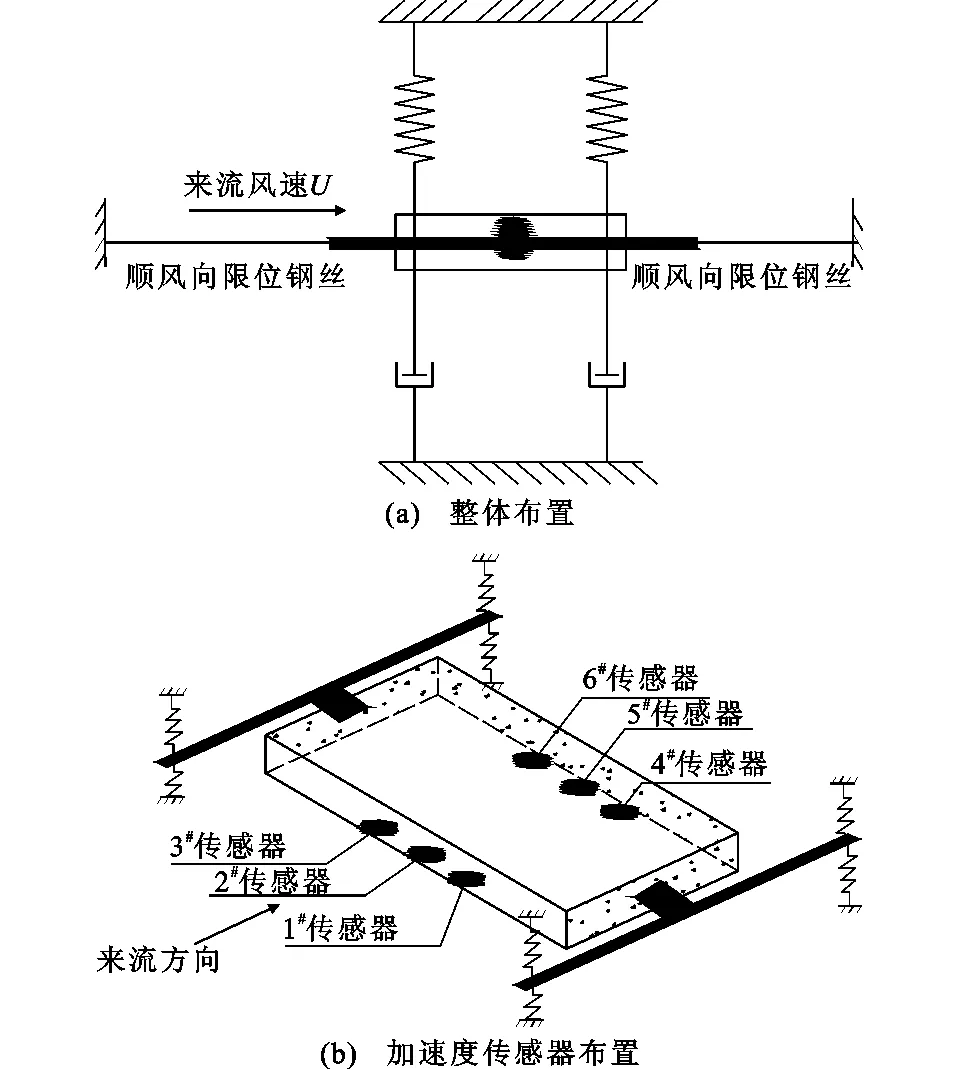
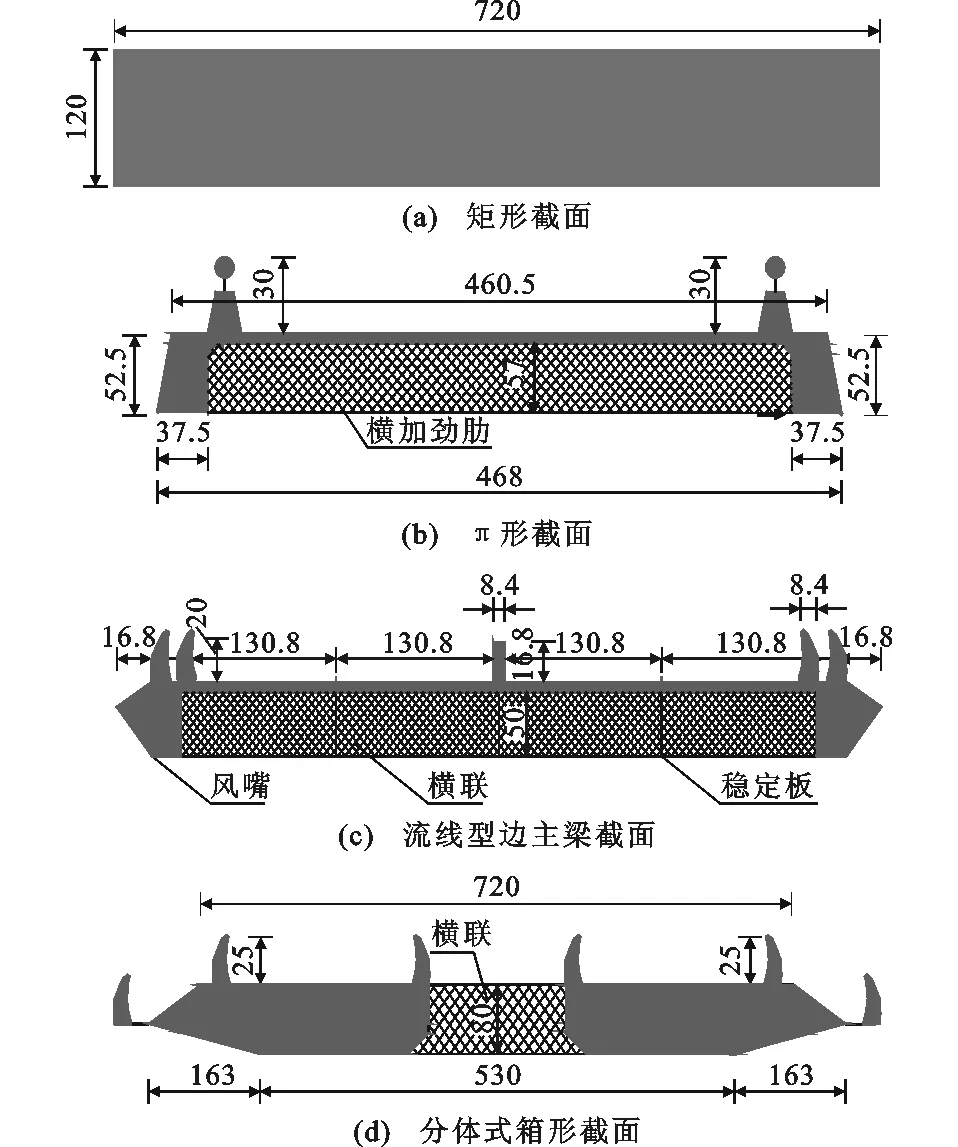
表1节段模型涡振试验工况Tab.1Working Conditions of Section Model Vortex Vibration Experiment

3.2降雨对结构的动力特性影响

为得到不同雨强下的模型动力特性，本文采用最小二乘曲线拟合模态参数识别法。因结构阻尼比和振动幅值密切相关，识别阻尼比参数时均截取相同的初始振幅来进行计算分析。基本原理为[15]：

对于实测的有阻尼自由衰减信号y(t)，其时间-位移变化关系可用下式拟合

Y(t)=Ae-ξωtcos(ωt+φ)

(25)

式中：Y(t)为实测信号的拟合值；A为振动初始幅值；ξ为结构机械阻尼比；ω为角频率；φ为初相位角。

通过对实测信号按照式(25)进行最小二乘拟合，则可得到上述模态参数的取值。拟合目标是使实测值y(t)和拟合值Y(t)之间的残差es最小，其可表达为

(26)

式中：Y(ti)，y(ti)分别为ti时刻结构响应的拟合值与测试值；t1，tn分别为与响应相对应的初始和结束时刻。

节段模型频率和阻尼比随试验雨强的变化规律见图7，8。由图7可知：随着试验雨强的增大，模型的振动频率会相应减小，各类模型断面频率变化率在120 mm·h-1的最大试验雨强时均处于1.5%～3.5%之间。另外，雨强超过60 mm·h-1后，振动频率随雨强的增长而减缓，依据坡面积水特征的分析可知：随着雨强的增大，模型断面的排水速度加快，这是因为水的聚合力有限，积水达到一定程度后其聚集的厚度不再发生改变。通过表1给出的雨强相似比计算得知：除去无原型的矩形截面外，其余节段模型试验雨强换算至实际后，雨强120 mm·h-1对应的实际雨强为600～700 mm·h-1，这一范围的雨强值基本达到了100年一遇的极端情况，因此一般常规雨强下，频率随雨强的变化非常小。

由图8可知：随着雨强增大，机械阻尼比一直增加，试验雨强达到120 mm·h-1时，除矩形断面外，阻尼比增量绝对值处于0.05%～0.15%的范围(雨强相似比为1∶1)，其与雨滴的冲击力和表面积水黏滞力相关。

3.3风雨耦合作用时结构的涡振响应

通过传感器获取测点的振动加速度响应，按照公式(27)计算竖弯和扭转涡振，即

(27)

式中：ah，aα分别为考虑多测点、长时段采用平均化处理后的竖向和扭转加速度响应；k为测点布置数目，根据图5(b)可知k=6；ai为对应于i测点加速度传感器所测得的响应信号。

由于节段模型的竖弯和扭转涡振频率惟一，加速度响应换算至位移时可以直接采用三角函数作为被积函数进行频域积分，积分所得的各节段模型涡振量纲一的位移振幅如图9，10所示。由图9，10可知，有雨时的涡振振幅绝大部分均小于无雨时的结果。涡振的其他关键特性(包括涡振区间数目、长度以及最大振幅对应的约化风速等)并无明显改变。值得注意的是，随着雨强的增大，部分试验的振幅[图9(a)，图10(b)]出现先减小后增大的趋势，表明小雨时阻尼的增大大幅减小了涡振振幅，而在大雨时，雨滴冲击引起的动力响应可能会起主导作用从而增大振幅。根据表1给出的雨强相似换算关系，计算后得到的实际雨强均大于615 mm·h-1，最大为2.6×104mm·h-1，故实际降雨对涡振响应的影响十分有限，除非极端特殊状况，常规雨强的影响可以忽略。

以上试验结果可以从雨滴做功的角度予以分析解释，对于风雨耦合作用下的主梁断面，以竖向振动为例，在结构简谐运动的一个周期时间内，根据动量定理可获得主梁分别向下和向上运动时雨滴的动量方程，即

(28)

式中：vr0为质量加权等效后的雨滴竖向速度；vs为结构运动的竖向速度；mrs为时间τ内落入主梁表面的雨滴质量总和；Frv1，Frv2分别为主梁向下和向上运动时的雨滴平均冲击作用力。

主梁向上和向下运动半个周期，向上雨滴冲击力做负功，向下做正功，故由此可知在整个周期内雨滴冲击力对结构做的功Wrv为[4,15]

(29)

式中：T为主梁做简谐振动时一个周期内向上和向下的运动位移总和。

由此可知：一个周期内雨滴冲击是做负功的，有利于减小振动，经过同样的推导可获知这一结论也适用于断面扭转运动和表面积水时的做功分析。

4结语

(1)根据降雨冲击力和在结构表面的积水特征，由风雨作用三分力、质量以及外形等参数量纲一的特征值一致原则可以推导相应的雨强相似比。对于频率测试等只与质量相关的试验时，可采用只考虑表面积水质量的雨强相似比。无风时的机械阻尼特性试验雨强相似比取为1∶1。对于涡振和颤振等竖向的主梁动力响应试验，可采用只考虑雨滴竖向冲击的雨强相似比。

(2)主梁截面振动频率随雨强的增大会相应减小，其为模型积水厚度引起质量改变而造成。主梁的机械阻尼随着雨强的增大有所增加，其与雨滴冲击力对结构运动的阻碍以及表面积水流动引起的摩阻耗能有关。依据本文推导的简化雨强相似比可知，降雨对主梁振动频率的改变可以忽略，较强雨强下机械阻尼才增加明显，其影响有限。

(3)随着雨强的变化，主梁涡振的区间数目、区间长度(起振和结束风速)以及最大振幅对应的风速无明显变化，说明涡振的发展规律不因降雨而改变。有雨时主梁的竖弯和扭转涡振振幅基本小于无雨时的结果。小雨时阻尼对竖弯和扭转涡振振幅的抑制作用占主导，雨强超过一定值后，雨滴动力冲击效应变得显著。根据本文推导的雨强相似比可知，涡振试验的最大雨强原型值均超过615 mm·h-1左右的中国雨强极值，故可认为常规雨强对实际主梁涡振响应的影响十分有限。

参考文献：

References:

[1] 陈政清.桥梁风工程[M].北京:人民交通出版社,2005.

CHENG Zheng-qing.Bridge Wind Engineering[M].Beijing:China Communications Press,2005.

[2] 许福友,丁 威,姜 峰,等.大跨度桥梁涡激振动研究进展与展望[J].振动与冲击,2010,29(10):40-49.

XU Fu-you,DING Wei,JIANG Feng,et al.Development and Prospect of Study on Vortex-induced Vibration of Long-span Bridges[J].Journal of Vibration and Shock,2010,29(10):40-49.

[3] XIN D B,LI H,WANG L,et al.Experimental Study of Rain Effects on Vortex Shedding of Long Span Bridge Girders[J].Advances in Structural Engineering,2012,15(10):1793-1799.

[4] 辛大波,张明晶,王 亮,等.大跨度桥梁主梁风雨致涡激振动试验研究[J].哈尔滨工程大学学报,2011,32(9):1168-1172.

XIN Da-bo,ZHANG Ming-jing,WANG Liang,et al.Experimental Study on Wind-rain-induced and Vortex-induced Vibration in Bridge Deck Sections of Long-span Bridges[J].Journal of Harbin Engineering University,2011,32(9):1168-1172.

[5] 武占科.风雨共同作用结构荷载模型及参数的试验研究[D].上海:同济大学,2009.

WU Zhan-ke.Experimental Research of the Structure’s Load Model and Its Parameters in the Condition of Wind Driving Rain[D].Shanghai:Tongji University,2009.

[6] BILANIN A J.Scaling Laws for Testing Airfoils Under Heavy Rainfall[J].Journal of Aircraft,1987,24(1):31-37.

[7] CAO Y H,WU Z,XU Z L,et al.Effects of Rainfall on Aircraft Aerodynamics[J].Progress in Aerospace Sciences,2014,71:85-127.

[8] SURRY D,R,INCULET D R,SKERLJ P F,et al.Wind,Rain and the Building Envelope:A Status Report of Ongoing Research at the University of Western Ontario[J].Journal of Wind Engineering & Industrial Aerodynamics,1994,53(94):19-36.

[9] 唐顺勇,李宏男.输电塔气弹模型制作及风雨荷载的相似比研究[J].振动与冲击,2011,30(8):199-202.

TANG Shun-yong,LI Hong-nan.Aeroelastic Modeling of Transmission Towers and Similarity Ratio for Wind-rain Loads[J].Journal of Vibration and Shock,2011,30(8):199-202.

[10] MARSHALL J S,PALMER W M K.The Distribution of Raindrops with Size[J].Journal of the Meteorology,1948,5(4):165-166.

[11] GUNN R,KINZER G D.The Terminal Velocity of Fall for Water Droplets in Stagnant Air[J].Journal of the Meteorology,1949,6(4):243-248.

[12] CHOI E C C.Wind-driven Rain and Driving Rain Coefficient During Thunderstorms and Non-thunderstorms[J].Journal of Wind Engineering & Industrial Aerodynamics,2001,89(3/4):293-308.

[13] 刘庆宽,乔富贵,杜彦良.降雨对基本构件气动特性影响的初步研究[J].石家庄铁道学院学报:自然科学版,2007,20(4)14-18,44.

LIU Qing-kuan,QIAO Fu-gui,DU Yan-liang.Initial Research of Precipitation Effect on Aerodynamic Characteristics of Basic Bluff[J].Journal of Shijia-zhuang Railway Institute:Natural Science,2007,20(4):14-18,44.

[14] 季天剑.降雨对轮胎与路面附着系数的影响[D].南京:东南大学,2004.

JI Tian-jian.Influence of Rainfall on Adhesion Coefficient of Tire and Road Surface[D].Nanjing:Southeast University,2004.

[15] 雷 旭.大跨度桥梁柔细构件风(雨)作用及其振动控制研究[D].长沙:湖南大学,2015.

LEI Xu.Study About Wind (Rain) Effects and Vibration Control of Flexible Structural Members in Long-span Bridge[D].Changsha:Hunan University,2015.