基于改进自适应布谷鸟算法的云制造资源配置优化研究*

杨喜娟 杨 博 武 福

(①兰州交通大学电子与信息工程学院，甘肃 兰州 730070; ②兰州交通大学机电工程学院，甘肃 兰州 730070)

云制造资源配置优化问题是实现云制造智能化、高效化的关键问题。资源配置的优化可以解决目前大多数制造企业存在的资源闲置、能耗巨大、产能过剩等问题，改善制造业困境，提高服务质量和效率[1-3]。近年来，围绕云制造资源配置优化的研究热点主要集中在：①评价指标的研究；②服务评价综合方法的研究；③求解资源优化模型的方法研究。例如：文献[2]用基于灰色关联度分析的优选分析方法探讨了资源优化组合的求解过程；文献[4]基于模糊层次分析法建立了制造资源评价模型；文献[5]针对制造云服务组合问题建立模型并利用改进遗传算法求解；文献[6]采用改进的进化多目标算法对云制造资源配置双层规划模型进行求解；文献[7]提出用离散型粒子群遗传混合算法对云制造配置模型进行求解。但是，遗传算法参数多、收敛速度较慢、会产生大量冗余迭代；粒子群算法易早熟、易陷入局部最优，搜索质量不高；蚁群算法收敛速度慢、易停滞、易陷入局部最优。因此需要更为简单、可靠、高效的算法求解资源配置优化问题。

基本布谷鸟搜索算法(CS)是2009年由剑桥大学Yang等学者提出的一种新的全局优化启发式算法，它主要模拟自然界布谷鸟飞行以及寄生行为，通过Levy飞行机制寻找寄主鸟窝，即更新每代解实现全局搜索，再经过Biased随机游走方式淘汰并改善部分解，以达到局部搜索最优的目的。布谷鸟算法具有参数少、全局搜索能力强、不易陷入局部最优、鲁棒性好、通用性强、简单高效、易操作等显著优势，目前广泛用于解决函数优化、资源调度、工程结构优化、TSP等诸多问题中[8-9]。但是，基本布谷鸟算法也存在一些缺陷，例如：搜索后期收敛速度较慢、缺少活力等。因此有许多学者除了对算法的步长、参数和发现概率做积极改进之外，还在与其他算法相耦合方面不断研究创新。文献[10]提出的布谷鸟搜索增强算法采用逐维评价策略接收部分进化个体，增强算法的求精能力和收敛速度；文献[11]引入动态惯性权重改进解的更新方式，依据动态惯性权重值保留上代鸟窝的最优位置，并进行下一代位置更新，从而有效平衡种群探索能力和开发能力之间的关系；文献[12]提出基于粒子群算法的布谷鸟搜索算法，进一步提高布谷鸟算法的求解精度和收敛速度；文献[13]提出一种基于适应值分配的自适应步长和发现概率的布谷鸟搜索算法，提高了算法的计算精度；文献[14]将混沌理论引入布谷鸟搜索算法，使混沌特性与基本布谷鸟算法相结合，进一步提高了布谷鸟算法性能。

针对其他启发式算法易早熟、易陷入局部最优、收敛质量不高等问题，本文提出了一种改进自适应布谷鸟搜索算法，并将其应用于云制造资源配置模型的求解中，为云制造资源优化配置提供了新的思路。

1 问题描述与模型建立

云制造资源配置优化问题描述如下：一客户企业在云制造平台定制生产一套电气设备，当客户将制造需求和约束条件上传至云制造平台后，平台首先将此套电气设备生产任务视为总任务J，并将其分解为n项生产分任务,可以表示为N1,N2,N3,…,Nn,接着云制造平台会从资源库中搜索并收集满足客户需求的资源，每项分任务对应若干个资源，可分别表示为N1M1,N1M2,N1M3,…,N2M1,N2M2,N2M3,…,NnMm，如果无合适资源，则客户应当修改约束条件进行重新搜索，最后云制造平台将根据各资源的性能参数，运用资源精选数学模型予以计算，求得满足客户要求的最优资源服务链。

资源精选数学模型主要由体现生产高效性的总时间值T、表现资源经济性的总成本值C、反映资源可靠性的总质量值Q、体现服务高效性与准确性的总管理值M以及折射客户资源满意度和信任度的总反馈值F五项评价指标构成。在将五项指标代入精选数学模型计算之前还需要对数据进行相应处理：

步骤1 因为各指标间计量单位和数量级都不同，不能直接进行综合分析，所以需要对指标数据去量纲化处理。方法是均值法：E=H/h，其中H为各指标参数，h表示所有备选资源每项指标的平均值。

步骤2T、C是成本型指标，必须转化为效益型指标，方法是E0=Emax-E，其中Emax表示客户允许的最大总时间T和最大总成本C。

步骤3 将效益型指标Q、M和F定量化处理，如表1所示，其中2、4、6、8 表示中间值。

表1 定量化赋值标准

为了简化问题，从以上五指标出发，运用线性规划法建立的最优资源精选数学模型如下:

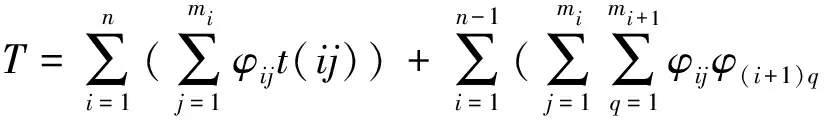
(1)

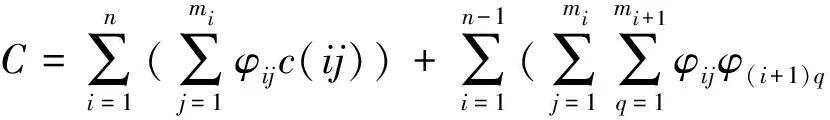
(2)

(3)

(4)

(5)

总目标函数：maxZ=w1T0+w2C0+w3Q+w4M+w5F

(6)

数学模型中：φij∈{0,1}为决策因子，当φij=1时，表示第i个子任务由第j个资源参与制造，否则φij=0；当δ=0时，表示分任务Ni对应的制造资源Mj与分任务Ni+1对应的制造资源Mq之间存在着信息流，δ=1时，两者间存在着物料流；q表示第i+1个子任务中的第q个服务资源；n代表共有n种生产分任务；mi代表第i项分任务对应符合要求的资源有m种；t(ij)代表分任务Ni对应制造资源Mj所需加工时间；t(ij,(i+1)q)代表分任务Ni中第j个资源和分任务Ni+1中第q个资源的连接时间；c(ij)代表分任务Ni对应制造资源Mj所需加工成本；c(ij,(i+1)q)代表分任务Ni中第j个资源和分任务Mi+1中第q个资源的连接成本；qj(i)代表分任务Ni对应资源Mj的制造质量合格值；mj(i)代表分任务Ni对应资源Mj的服务管理值；fj(i)代表分任务Ni对应资源Mj的动态反馈值。Tmax、Cmax、Qmin、Mmin、Fmin分别为反映客户底线要求的最后总时间、最大总成本、最差平均质量、最差平均管理和最差平均反馈值。完成整个过程的最长时间要小于等于客户允许的最后时间；所需的成本要小于等于客户给定的最大成本；质量均值必须大于等于客户的最差质量要求；管理均值必须大于等于客户的最差管理要求；反馈度均值必须大于等于客户的最差反馈要求。此外，w1、w2、w3、w4、w5分别表示时间、成本、质量、管理及反馈的权重值，且w1+w2+w3+w4+w5=1，各权重值计算过程如下：

步骤1 通过对评价指标间重要性的定量比较，建立出判断矩阵A，A中的元素为aij(i，j=1,2,3,4,5)，指标重要性量化如表2所示。

步骤2 利用公式xij=aij/(a1j+a2j+a3j+a4j+a5j)对矩阵A中的元素aij进行处理，其中xij(i，j=1,2,3,4,5)表示处理后的元素。

步骤3 根据公式wi=xij/5再对矩阵A进行归一化处理，其中wi(i=1,2,3,4,5)表示计算得到的权重值。

表2 指标重要性量化

2 改进算法的优化原理

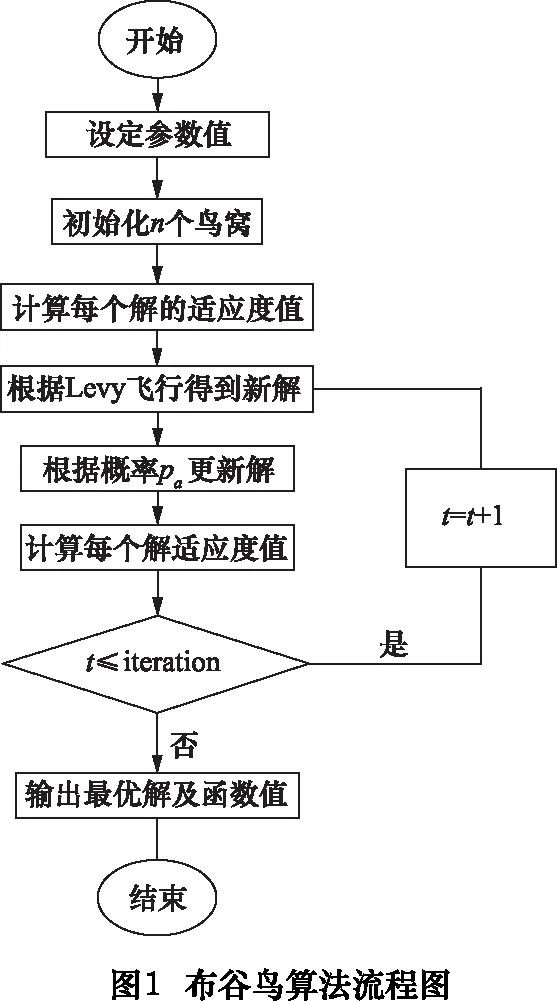
布谷鸟算法是由Yang Xinshe和Deb Suash在2009年提出的一种新的启发式算法，它根据自然界鸟类或果蝇飞行规律，模拟布谷鸟寄生育雏的策略，提出两个核心算法组件：Levy飞行和Biased随机游走。在Levy Flights随机游走中，每一代种群里的每个个体Xi分别以当代最优个体Xbest为导向，搜索新的个体Xi+1,飞行步长满足Levy分布，更新公式为：

(7)

其中：α0为比例因子，通常取0.01；β为常数，通常取1.5；u、v为满足正态分布的随机数，另外：

(8)

其中：Γ表示伽马方程。

在Biased随机游走中一般设定发现概率Pa为0.25，当缩放因子r∈[0,1]小于Pa时，保留原解；当缩放因子r大于Pa时，则根据Biased游走公式重新生成相同数量的新解。具体更新公式如下：

Xi=Xi+r(Xj-Xk)

(9)

基本布谷鸟算法具体运算流程如图1所示。

改进自适应布谷鸟算法(SAACS)是在基本布谷鸟算法(CS)的基础上通过自适应调整部分参数，加入双向搜索策略，并引入模拟退火算法的思想后得到的，具体流程如图2所示，其具体改进有以下几个方面：

其一，在Levy Flights随机游走寻找新解过程中的步长越大，全局搜索得到的解多样性增加，搜索速度加快，更容易靠近最优解，但是搜索精度会相应降低；而步长越小，更有利于局部搜索，搜索精度得到提高，但是搜索速度变缓。因此，应该令比例因子α0和常数β随着迭代次数以及适应度质量自适应调整，使运算过程在迭代初期、适应度值较差的情况下扩大搜索范围，增强全局搜索的能力，增加解的多样性，而在迭代后期缩小搜索范围达到精确搜索的目的。具体调整如下：

其中：n表示种群大小；αmax表示比例因子最大值；αmin表示比例因子最小值；βmax表示β最大值；βmin表示β最小值；σ1、σ2分别代表正态分布的方差；u代表正态分布的均值；t表示当前迭代次数；T表示迭代总次数；fi表示适应度值。

其二，在Biased随机游走过程中，将缩放因子r的取值范围由[0,1]调整为[-1,1]，令单项搜索转换为双向搜索，在一定程度上保持了群体的多样性，引导搜索过程向最优解逼近，增强局部搜索效率，加快搜索最优解速度。

其三，将模拟退火思想引入改进算法中。经过Biased随机游走得到新解之后，计算新解的适应度值，并在适应度择优后保留较优解，而到迭代后期步长变为很小的情况下，计算陷入局部最优的风险较大，因此对于淘汰解可用min(1,e-Δf/T)≤rand[0,1]进行随机保留，随着迭代次数增加，温度降低，接受淘汰解的概率逐渐变大，可以在每次迭代后增加种群的多样性，避免陷入局部循环。

3 改进算法的实现

类似于资源调度等离散型问题，在运用改进自适应布谷鸟算法时，应该对各项任务相应资源构成的组合方案进行编码，如：对资源N1M3、资源N2M1、资源N3M4、资源N4M2、资源N5M1、资源N6M2、资源N7M1、资源N8M3组成的方案编码为(3,1,4,2,1,2,1,3)。改进后的自适应布谷鸟算法(SAACS)应用于求解云制造资源配置优化的数学模型中。运算步骤如下所示：

步骤1 对各项分任务相应资源构成的组合方案进行编码，设定退火温度Q等一系列参数值。

步骤2 随机初始生成n个鸟巢，即n个资源组合方案。

步骤3 将初始种群中生成的每个资源组合解全部解码，检验各组合方案是否满足式(6)中的约束条件，并根据处理后的参数计算出各自函数值，作为初始适应度值。

步骤4 根据Levy飞行在初始种群基础上生成新的解，其中参数β和步长α采用自适应方式。

步骤5 根据被发现概率pa，运用双向搜索策略搜索新解以替换旧解，并检验新种群中每个资源组合是否满足式(6)中的约束条件。

步骤6 计算得到每种资源组合的适应度值，在进行适应度择优后得到较优解，对于其他解则用min(1,e-Δf/T)≤rand进行随机保留。

步骤7 判断是否符合循环终止条件，如果不符合跳转步骤4。

步骤8 若符合终止条件，则再次计算得到每种资源组合的适应度值，选择出适应度最小的解，即可得到最优资源组合以及最大函数值。

4 实验分析

现以某公司需要的智能通信配电设备生产为问题的实际应用场景，将可以互相替代并可以移动的活动生产工位封装成制造云服务，在全部零部件生产中挑选部分核心零部件为代表进行试验。仿真试验环境为2.20 GHz Pc,2 G内存，Windows7 64位操作系统，Matlab R2012b。

依据文献[15]的算例模型，客户将制造任务提交云制造服务平台后，制造任务主要被分为配电柜生产和机柜生产两项任务，其中配电柜包含门、顶底板等生产分任务，而机柜包括隔板、内立柱等生产分任务。具体加工任务分解如表3所示。

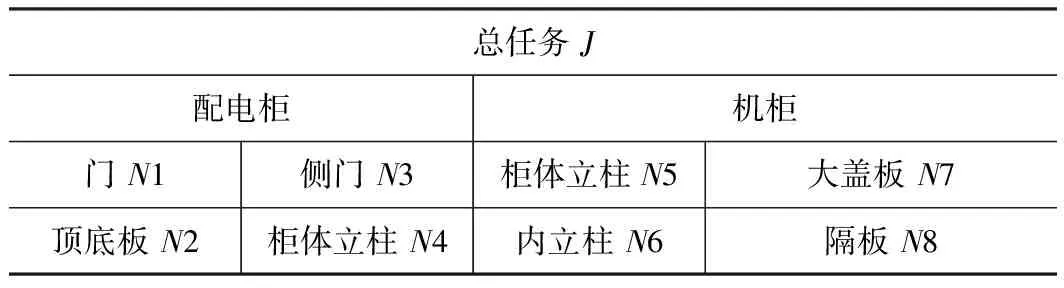
表3 加工任务分解

平台接受任务后首先立即在资源库中进行“资源匹配”，建立出符合生产需求的初选资源集，如表4所示。

表4 各资源的量化

接着根据客户按实际需求列出指标重要性判断矩阵A：

经过计算并归一化处理后，得到矩阵A中的各指标权重值如表5所示,这5个权重值分别对应(6)式中的w1,w2,w3,w4,w5。

表5 式(6)中的各个权重值

实验一 算法有效性验证

根据表4中各资源去量纲、指标转化后的参数，分别利用基本布谷鸟算法(CS)、自适应布谷鸟算法(ACS)[13]以及改进自适应布谷鸟算法(SAACS)对资源配置优化精选模型进行求解。设定初始种群数为n=30，全局迭代次数iteration=200，发现鸟窝的概率pa=0.25，函数参数个数nd=8，比例因子最大值αmax为0.5，比例因子最小值αmin为0.05，βmax为1.8，βmin为0.8，σ1、σ2分别为0.3和0.005，初始温度Q=500，退温方式为：Qt+1=aQt，其中冷却系数a取0.5，Qt为第t次迭代的温度，Tmax=45.12,Cmax=3944,Qmin=6，Mmin=5，Fmin=5。经过MATLAB运算后，适应度值变化曲线如图3所示。

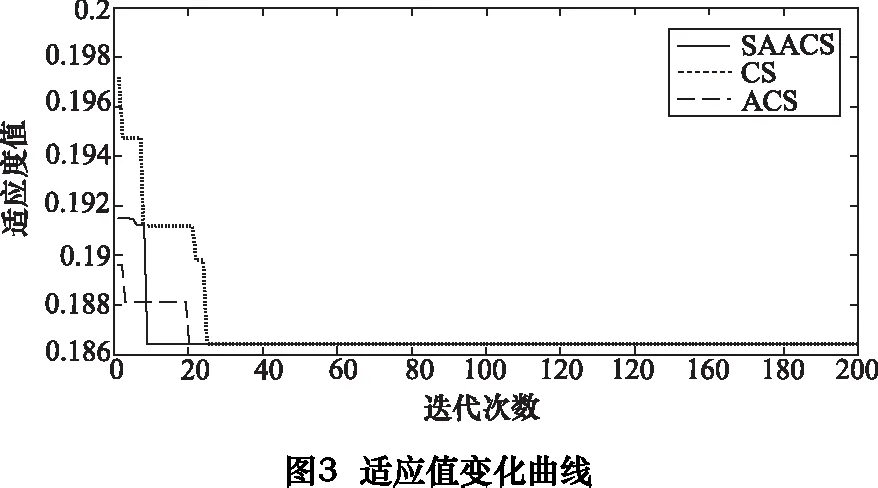
从图3可以看出大约30代以后种群适应度值趋于稳定。最终得到的最小适应度值为0.1864，总目标函数最大值maxZ为5.3648，对应最优资源组合方案为：资源N1M3、资源N2M3、资源N3M4、资源N4M3、资源N5M1、资源N6M3、资源N7M2、资源N8M2，完成总任务的总时间为34.44h，完成总任务的总成本为2 821元。实验充分证明：改进自适应布谷鸟算法在求解云制造资源配置模型方面是可行有效的。

实验二 算法准确度验证

根据表4中各资源去量纲、指标转化后的参数，在相同种群规模n=50、相同迭代次数iteration=200和相同问题规模nd=8的情况下，分别运用基本布谷鸟算法(CS)、自适应布谷鸟算法(ACS)[13]及改进自适应布谷鸟算法(SAACS)对精选数学模型进行100次求解实验，对比探究新算法求解的准确度，结果如表6所示。

表6 3种算法的计算准确度与收敛所需迭代次数对比

从表6对比结果可以看出，SAACS求解准确率明显高于另外两种算法，并且在相同条件下，SAACS的迭代次数更少于其他算法。因此，改进自适应布谷鸟算法在求解云制造资源配置模型的准确度方面更符合要求。

实验三 算法效率验证

根据表4中各资源去量纲、指标转化后的参数，在不同种群规模、不同迭代次数和扩大问题规模的情况下运用改进自适应布谷鸟算法对精选数学模型进行求解，探究新算法的求解效率，结果如表7所示。

表7 SAACS运算时间

表7中运行时间单位为“秒(s)”，各种情况下每项实验做十次取平均值，问题规模nd扩大部分的参数依据N1Mj(j=1,2,3)和N2Mj(j=1,2,3,4)。从表7中可以体现出随着种群规模、问题规模和迭代次数的单方面变化，SAACS运算时间基本也成线性变化，另外还进一步表明改进自适应布谷鸟算法在求解各种规模问题上的可行性和高效性。

5 结语

本文以基本布谷鸟算法为基础，通过自适应调整步长、动态调整参数，应用双向搜索策略和模拟退火思想，提出了改进自适应布谷鸟算法(SAACS)，并将该算法运用于求解云制造资源配置优化模型中。经过实验证明，新算法不仅是有效、可行的，而且在求解效率和准确度方面都优于同类算法。改进自适应布谷鸟算法为云制造环境下最优资源服务链的快速获得提供了一种新的思路和方法。

[1] 胡艳娟,武理哲，张霖，等.云制造服务评价理论与方法研究综述[J].计算机集成制造系统，2017，23(3):640-649.

[2]尹超,张云，钟婷.面向新产品开发的云制造服务资源组合优选模型[J].计算机集成制造系统，2012，18(7):1368-1378.

[3] Zhang L,Luo Y,Li BH,et al. Cloud manufacturing: a new manufacturing paradigm[J]. Enterprise Information Systems，2014,8(2): 167-187

[4]张元龙,屠建飞,谢文东.基于模糊层次分析法的云制造资源评价[J].机械制造，2015，53(6):49-52.

[5]刘卫宁,刘波，孙棣华，面向多任务的制造云服务组合[J].计算机集成制造系统，2012，19(1):199-209.

[6] 苏凯凯，徐文胜，李建勇.云制造环境下基于双层规划的资源优化配制方法[J].计算机集成制造系统，2015，21(7):1941-1952.

[7]武善玉,张平,覮李方.云制造系统中基于粒子群优化的多任务调度[J].华南理工大学学报，2015，1(43):105-110.

[8]兰少峰,刘升.布谷鸟搜索算法研究综述[J].计算机工程与设计，2015，(4):1063-1067.

[9]李志平,王 勇,张呈志.云模型的布谷鸟搜索算法[J].计算机应用研究,2016.(1):93-97.

[10]林要华，王维.基于逐维策略的布谷鸟搜索增强算法[J].计算机工程与科学，2017，39(1):165-172.

[11]周欢，李煜.具有动态惯性权重的布谷鸟搜索算法[J].智能系统学报，2015(4):645-651.

[12]李娜，贺兴时.基于粒子群算法的布谷鸟搜索算法[J].纺织高校基础科学学报，2014(3):374-379.

[13]彭建新,詹志辉,陈宗淦，等.自适应步长和发现概率的布谷鸟搜索算法[J].济南大学学报：自然科学版，2016，30(5):328-333.

[14] GaiGe Wang,S Tab.AH Gandow,et al. Chaotic cuckoo search[J]. Soft Comput，2016,20(9):3349-3362.

[15]王时龙,宋文艳，康玲，等.云制造环境下的制造资源优化配置研究[J].计算机集成制造系统，2012，18(7)1:396-1405.