火灾下矩形钢筋混凝土梁柱温度场的CA模拟

陈梦成，谢 力，刘 超，陈娜茹

(1.南昌大学 建筑工程学院，江西 南昌 330031;2.华东交通大学 土木建筑学院，江西 南昌 330013)

随着建筑物高层化、大规模化，火灾造成的损失也不断增大，对结构进行抗火设计具有重要意义。在高温下，钢筋混凝土结构发生复杂的物理化学变化，致使结构发生显著变形。温度场分布不仅是力学性能分析的前提，也是火灾后修复加固的依据。由于材料的热工性能参数是随着温度-时间曲线的变化而变化的，因此钢筋混凝土构件截面的导热问题是一个非线性瞬态问题。目前国内外学者主要采用有限差分法和有限元法解决受火钢筋混凝土温度场计算问题。文献[1]采用对角线网格法给出了二维温度场的差分格式。文献[2]利用有限单元法编制了高温下钢筋混凝土异形柱的温度场分析程序。文献[3]利用有限单元-差分混合分析法对二维温度场进行了分析计算。文献[4]对三面受火钢筋混凝土柱进行了温度场以及力学性能试验研究。文献[5]分别对一面、两面、三面受火的简支梁进行了抗火性能试验研究。

近年来，元胞自动机已成功应用于模拟混凝土结构耐久性分析中涉及的扩散过程[6]，在建筑物耐火性分析中的温度场模拟也取得了一定成果[7]。本文基于元胞自动机理论，通过引入高温下混凝土的热工性能参数，建立钢筋混凝土结构的元胞自动机传热模型，分析与讨论不同受火方式及时间对钢筋混凝土梁截面内温度分布的影响。钢筋混凝土是一种各向异性、非均质的复合材料。在实际中，当构件的尺寸大于骨料粒径的4倍，一般可假定混凝土是各向同性材料，而钢筋在钢筋混凝土结构中所占体积很小，且钢材的传导系数值很大，在计算构件截面的温度场时可以忽略钢筋的“贡献”[8]。在元胞自动机理论中，可用钢筋位置的混凝土元胞温度代替钢筋的温度。

1 高温下混凝土的热工性能

1.1 混凝土的导热系数

导热系数λ采用文献[9]建议的随温度T(20 ℃≤T≤1 200 ℃)变化的公式，按上下限分为：

导热系数上限

(1)

导热系数下限

(2)

1.2 热辐射系数

根据Stefan-Boltzmann定律[10]，热辐射系数为b=σnεrφ。其中史蒂芬-玻尔兹曼常数σn=5.67×10-8W/(m2K4);εr为综合辐射系数，εr=εfεm，εf为与受火构件有关的辐射系数，一般取0.8,εm为与受火构件表面特性有关的系数，一般取0.625；φ为视角因子,一般取1。在辐射率较高时可取εr=0.7,较低时可取εr=0.3,当为理想辐射体或黑体时εr=1，一般取εr=0.5。

1.3 表面对流换热系数

混凝土表面和火源之间的传热主要受空气流动速度的影响，采用对流换热系数h描述，参照文献[11]，取h=25 W/(m2K)。

1.4 混凝土的质量热容

根据文献[9]建议的质量热容公式，含水率仅影响温度在100～200 ℃之间的质量热容。含水率为1.5%时，在100～115 ℃达到峰值 1 470 J/(kg·K)，在115～200 ℃ 线性下降至 1 000 J/(kg·K)。而含水率为0%时，从100 ℃的900 J/(kg·K)线性增大至200 ℃的 1 000 J/(kg·K)。含水率为0时的质量热容c为

(3)

1.5 混凝土的质量密度

在升温过程中，水分会随着温度的升高而损失，混凝土质量密度ρ有所下降，取温度T=20 ℃时，ρ20 ℃=2 300 kg/m3，采用文献[9]建议的表达式:

(4)

1.6 时间-温度曲线

为了模拟现场火灾的发展情况，ISO国际标准组织制定了一条理想化的理论试验曲线，称为标准时间-温度曲线[12]。本文除特别申明之处均采用该曲线模拟火灾的升温情况。

T=T0+345lg(8t+1)

(5)

式中：T0为室温，一般取20 ℃；t为升温时间,min；T为升温tmin后的温度,℃。

2 元胞自动机与热扩散

2.1 元胞自动机定义

(6)

式中:φ为元胞自动机的演化规则;r为元胞邻居半径。

由此可见，元胞邻居的合理选择直接影响到演化规则的有效性。图1给出了一些典型的一维和二维常用元胞邻居模式，当然还有很多其他更复杂的元胞邻居模式。一般来说，元胞邻居模式越复杂，演化规则的确定就越困难。

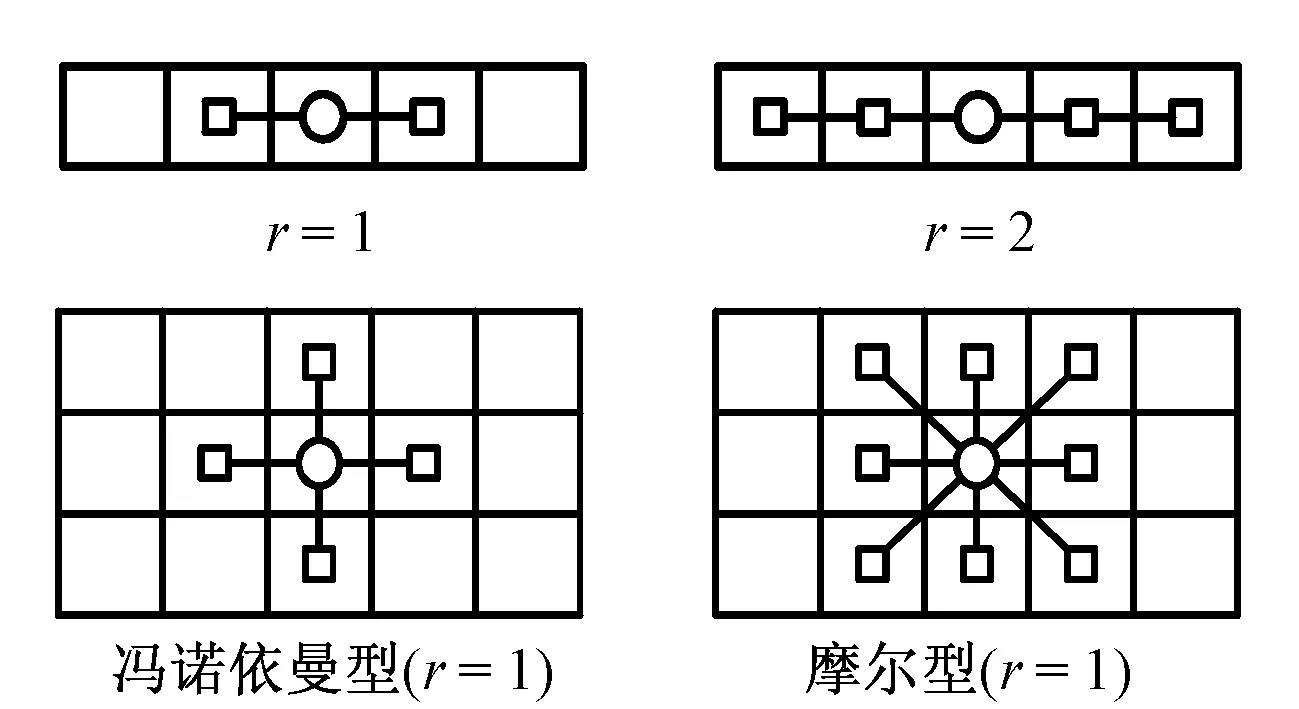
图1 元胞自动机元胞邻居模式

2.2 元胞自动机与热扩散关系

一般情况下任何满足微分方程的物理系统均可以由一个元胞自动机来描述。传热过程也可以用一个元胞自动机描述。本文拟采用二维冯诺依曼型的元胞自动机描述热扩散过程，其元胞邻居半径r为1，元胞自动机演化规则如下

(7)

(8)

根据传热理论[10],对一个大小为Δx的元胞自动机来说，在时间步长Δt内，有

(9)

(10)

(11)

(12)

其中

(13)

式中：D为热扩散系数，D=λ/cρ。

基于连续性原理，中心元胞的自身演化系数为

(14)

其中

(15)

当元胞邻居为一个辐射源时

(16)

当元胞邻居为一个非辐射源时Δφ=0。

为了确保计算结果满足精度要求，元胞尺寸Δx和时间步长Δt的选取必须满足某种稳定的平衡关系。在热扩散介质为各向同性且为均质的情况下，初始状态时的演化系数与元胞大小、时间步长以及热扩散系数存在初始平衡关系[13]为

(17)

3 热传导方程的元胞自动机求解

3.1 热传导方程

根据能量原理，一个质量密度为ρ的微元体dxdydz，忽略微元体内部自身发热，在单位时间内从其表面流入(或流出)的热量，必等于微体温度升高所吸收(或温度降低时放出)的热量，即可建立热传导方程[14]如下

(18)

式中:T为微元体的温度；c为微元体的质量热容；λ为微元体的导热系数；ρ为微元体的质量密度。

若杆系结构沿构件轴线的温度相同，式(18)可进一步简化为二维热传导方程，即

(19)

在微小升温时间段内，假定传热介质为均质各向同性材料(构件尺寸远大于骨料粒径，且在忽略钢筋影响的情况下，混凝土可视为均质各向同性材料[8])，则此时λ，c,ρ为常量，因此，式(18)进一步简化为

(20)

3.2 元胞自动机求解

(21)

式中,φl是局部演化系数，且0≤φl<1。

(22)

式中:Δt为元胞自动机进行局部演化规则的时间差；ΔXl为中心元胞与元胞邻居之间的距离。

根据传热学原理和热量守恒定律有

(23)

(24)

将式(24)代入式(23),有

(25)

比较式(25)和式(22)可知

(26)

假定所有元胞形状为大小相等的正方形，即ΔXl=al=δ,A0=δ·δ=δ2,则

(27)

将式(27)代入式(22)，并注意到δ=Δx=Δy，则方程可改写为

[T(x,y,t+Δt)-T(x,y,t)]/Δt=

-D·{[T(x,y,t)-T(x-Δx,y,t)]/Δx-

[T(x+Δx,y,t)-T(x,y,t)]/Δx}/Δx- (28)

D·{[T(x,y,t)-T(x,y-Δy,t)]/Δy-

[T(x,y+Δy,t)-T(x,y,t)/Δy]}/Δy

当Δx→0，Δy→0，Δt→0时有

比较式(29)、式(20)可知，CA可复原热传导方程。

4 CA模型应用

本节首先应用元胞自动机模型对现有2个火灾下钢筋混凝土构件试验进行验算，再就钢筋混凝土构件侧面4种不同受火方式对温度场分布影响进行分析计算与讨论。

4.1 试验验证

4.1.1 基准示例1

文献[3]对钢筋混凝土矩形梁三面受火情况进行了试验研究。矩形梁截面尺寸为200 mm×300 mm,受火时间为120 min，热电偶沿矩形梁截面竖向对称轴之上进行布置，分别在距梁底面25,75,150 mm 处，如图2所示。在使用元胞自动机模型数值计算过程中，单个元胞尺寸取Δx=5 mm，时间步长Δt=0.07 min，b=0.7σn，h=25 W/(m2·K)，导热系数采用上限由式(1)得到，含水率为0时的混凝土质量热容、混凝土质量密度和时间-温度曲线分别采用方程式(3)—式(5)。如图2中各点处升温曲线的元胞自动机模型进行计算结果参见图3，图3同时给出了文献[3]的试验结果，可以看出，两者吻合程度良好；图中两者之间有些误差的主要原因可能是CA计算所取的导热系数、质量热容与实际值有所偏差所致 。

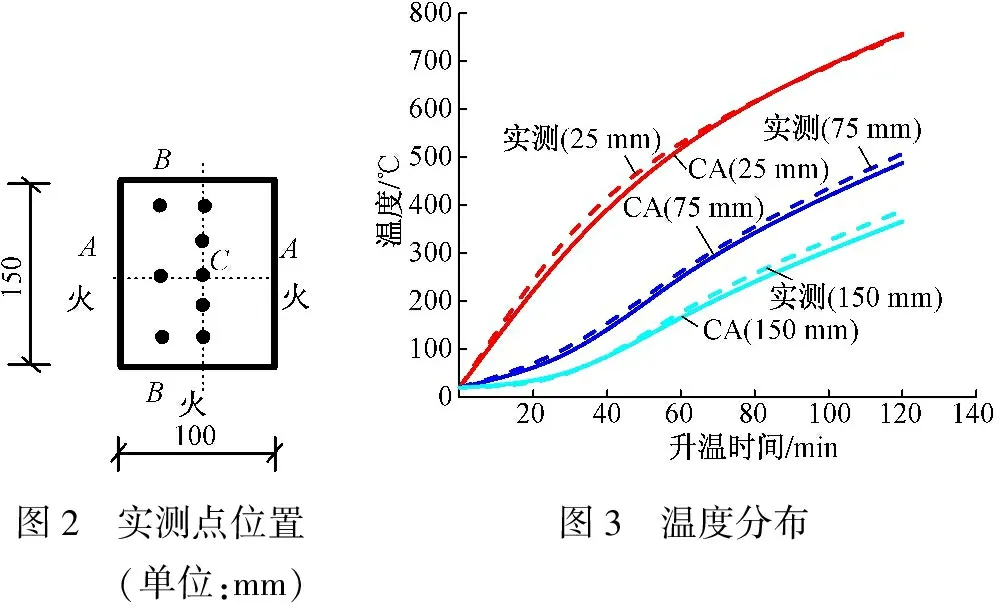
图2 实测点位置(单位:mm)图3 温度分布

4.1.2 基准示例2

2002年，胡海涛对三面受火的高强度混凝土压弯构件进行了试验研究[15]。构件截面尺寸为150 mm×200 mm，热电偶位置分布如图4所示。在利用元胞自动机CA模型对该试件温度场进行数值分析的过程中，取元胞尺寸Δx=1.874 mm，时间步长Δt=0.01 min，b=0.5σn，h=25 W/(m2·K),导热系数采用下限，由式(2)计算得到，含水率为1.5%的混凝土质量热容和混凝土质量密度采用文献[9]建议的表达式，分别参见本文式(3)和式(4)，混凝土的温控曲线采用文献[15]试验炉实测数据拟合出的升温曲线T=20+425.79lg(0.041t+1.056)，其中T为升温tmin后的温度。三面受火的高强混凝土压弯构件内沿其截面对称轴A-A和对称轴B-B上温度分布的元胞自动机CA模型数值计算结果分别如图5和图6所示，图中还相应地给出了文献[15]的实测结果。从图5可以看出，对称轴A-A上温度分布的元胞自动机数值模拟结果与文献[15]的实测结果吻合得比较好，但从图6来看，对称轴B-B上温度分布的元胞自动机数值模拟结果与文献[15]的实测结果吻合得不是很理想，误差相对较大。这主要有2方面的原因：①元胞自动机数值模拟中所用的混凝土热工性能值都是源于规范，这与试验中混凝土热工性能的实际值(文献[15]未给出)可能存在一定误差；②试验受周围环境的影响存在一定的离散性。

图4 热电偶位置(单位:mm)图5 截面对称轴A-A上温度分布曲线

图6 截面对称轴B-B上温度分布曲线

从以上2个试验基准示例的验证结果可以看出，元胞自动机的数值模拟结果与现有试验结果总体上吻合良好，说明本文运用的元胞自动机CA模型是可行、有效的。

4.2 应用算例

以矩形钢筋混凝土梁柱为例，研究不同受火方式对钢筋混凝土梁柱截面内温度场分布的影响。众所周知，在火灾作用下，混凝土的抗压强度会随着温度的升高而不断降低。当温度到达500 ℃时，混凝土的抗压强度损伤较为严重，约占常温下抗压强度的50%。本文参照文献[16]将截面温度>500 ℃的区域称为损伤严重区域。钢筋混凝土梁柱截面尺寸、钢筋布置和受火方式如图7所示。其中钢筋Bar 1形心的坐标为(40，40)。按受火方式分为4种不同工况。

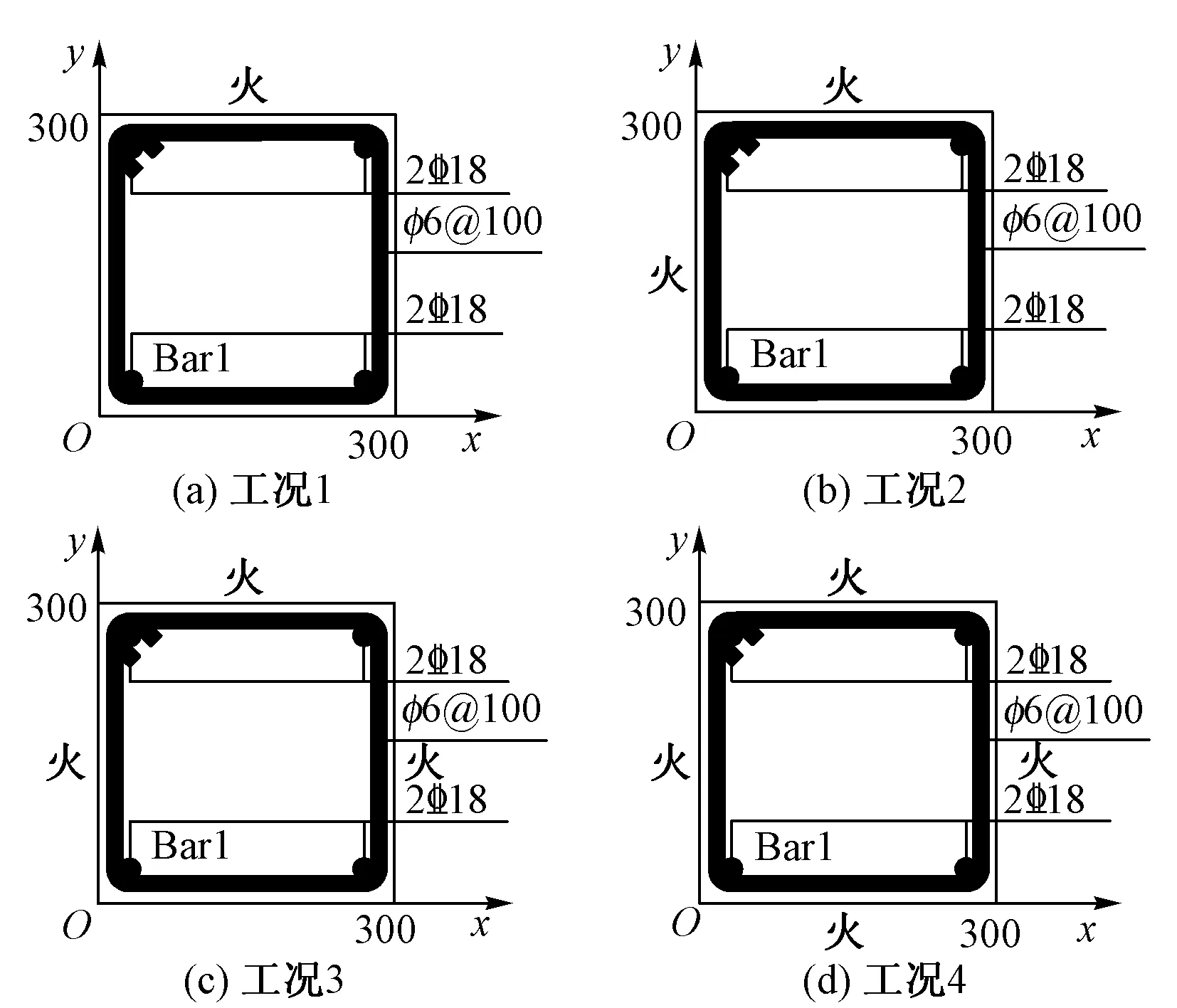
图7 受火模型(单位：mm)

4.2.1 温度损伤严重区域损伤分析

在元胞自动机CA模型数值模拟过程中，元胞尺寸取Δx=5 mm，时间步长Δt=0.07 min的元胞自动机，b=0.5σn,h=25 W/(m2·K)，导热系数采用上限，含水率为0时的混凝土质量热容、混凝土质量密度和时间-温度曲线分别采用式(3)—式(5)。利用元胞自动机CA模型计算得到的升温时间为1.0，2.0，3.0 h时的温度损伤严重区域截面分布图，参见图8。图中η代表的是温度损伤严重区域(云图部分)占矩形梁截面的面积，称为温度损伤严重区域损伤度。

从图8可知，钢筋混凝土受火方式对混凝土的损伤影响很大，在升温3.0 h内四面受火工况4混凝土损伤程度最大(78%)，其次为三面受火工况3，邻面受火工况2，单面受火工况1。随着升温时间的延长温度损伤区域所占面积不断增加，混凝土的最高温度不断提升，且总是从受火面向内部扩散，截面外表层温度梯度大，沿着截面向内温度逐渐下降，梯度亦呈下降趋势。

在4种受火形式下，除邻面受火工况2，其余工况下的温度均沿梁的截面轴线对称分布。各种工况下0.5，1.0，1.5，2.0，2.5，3.0 h时的钢筋混凝土梁柱温度损伤严重区域的损伤度η的CA模拟结果见图9，钢筋Bar 1温度随升温时间变化关系如图10所示。

图8 温度损伤严重区域截面分布

图9 η-升温时间关系曲线(单位：℃)

图10 Bar 1温度-升温时间关系

从图9可知，随着升温时间的延长，受火方式对温度损伤严重区域损伤度η不断增大，其中工况4的损伤度η变化最明显。钢筋混凝土梁柱受火温度损伤呈非线性变化，随着受火时间的推移，受火温度损伤将达到100%。

从图10可知，钢筋温度随升温时间的延长而不断增大，在工况1中，钢筋Bar 1离受火面较远，受火面引起的混凝土热传导在3.0 h内对钢筋温度的影响较小，致使钢筋的温度累积基本保持不变；在工况2，工况3中钢筋的温度变化趋势类似，是因为在这2种工况中仅一侧受火面离钢筋Bar 1较近，与工况1一样，受火面引起的热传导对其温度的影响较少，钢筋升温过程随受火面呈非线性增长，升温速度先快后慢；在工况4中，钢筋Bar 1因离两受火面较近，致使其升温加快，在3.0 h迅速达到876 ℃，但其升温过程表现出的规律与工况2、工况3类似。

4.2.2 温度-路径分布规律

如图11所示定义了2条升温路径，通过提取路径上的温度值，分析不同路径上的温度分布规律。图12(a)和图12(b)为升温3 h时各路径上的温度分布规律。

图11 路径示意

图12 温度-路径关系曲线(升温3 h)

从图12可知，在受火一侧温度最高，背火面一侧温度最低，温度沿截面轴线方向呈非线性变化，越靠近受火面，温度增速越快，当受火面对称时，温度亦呈对称分布，如工况1、工况3、工况4。

5 结论

本文建立了火灾下钢筋混凝土结构内部温度场分析的元胞自动机模型，并得到了现有试验结果的验证，说明本文建立的元胞自动机方法在钢筋混凝土结构温度场分析方面有效可行，而且应用潜力广阔。通过使用元胞自动机对不同受火方式下钢筋混凝土梁柱温度场分布的分析研究，得到以下结论：

1)通过选取合适的高温下混凝土的热工性能参数，元胞自动机模型可以实现钢筋混凝土结构温度场的高效、准确分析。

2)火灾下矩形钢筋混凝土梁柱温度损伤严重区域与受火方式、升温时间等紧密相关。四面受火情况下，温度损伤最为严重。

3)温度沿梁柱截面轴线方向呈非线性变化，越靠近受火面，温度增速越快;受火方式为对称受火时，温度亦对称分布。

4)钢筋混凝土梁柱受火损伤演化过程呈非线性变化，随着受火时间的推移，损伤程度达到100%。

5)钢筋升温速度与受火面数量及其位置有关，受火面越多，离钢筋越近，钢筋的升温速度越快；钢筋的升温过程呈非线性增长，先快后慢。

[1]LIE T T,IRWIN R J.Method Lo Calculate the Fire Resistance of Reinforced Concrete Columns with Rectangular Cross Section[J].ACI Structural，1993 90(1):52-60.

[2]WU B,XU Y Y.Nonlinear Finite Element Analysis of Transient Thermal Field for RC Special-shaped Columns in Fire[J].Proceedings of the Ninth International Symposium on Structural Engineering for Young Experts,2006,1/2:987-993.

[3]过镇海,时旭东.钢筋混凝土的高温性能及其计算[M].北京:清华大学出版社,2003.

[4]熊伟,李耀庄,严加宝.火灾作用下钢筋混凝土梁温度场数值模拟及试验验证[J].中南大学学报,2012,43(7):2838-2843.

[5]陆洲导，朱伯龙，周跃华.钢筋混凝土简支梁在火灾下反应的试验研究[J].土木工程学报，1993(3):47-54.

[6]陈梦成，袁素叶.多重因素下混凝土氯离子扩散CA模型及寿命预测[J],铁道建筑，2016,56(9):134-138.

[7]BIONDINI F,NERO A.Nonlinear Analysis of Concrete Structures Exposed to fire[C]//2nd fib Congress,Lausanne,Switzerland:FIB,2006.

[8]余志武,王中强，蒋丽忠.火灾下钢筋混凝土板的温场分析[J].铁道科学与工程学报，2004,1(1);58-61.

[9]European Committee for Standardization(CEN).EN 1992-1-2.Design of concrete structures Part1-2:General Rules Structural Fire Design[S].Brussels:2004.

[10]INCROPERA F P, de WITT D P.Fundamentals of Heat and Mass Transfer[M].New York:Wiley,2002.

[11]王卫华,董毓利.带楼板钢筋混凝土T形梁火灾下(后)温度场研究[J].中南大学学报(自然科学版),2015,46(2):684-693.

[12]资伟，余志武,匡亚川,等.受火温度和时间对喷水冷却后混凝土剩余抗压强度的影响[J].中南大学学报(自然科学版)，2013,44(4):1545-1550.

[13]FABIO B,ANDREA N.Cellular Finite Beam Element for Nonlinear Analysis of Concrete Structures Under Fire[J].Journal of Structural Engineering,2011,137(5):543-558.

[14]时旭东，过镇海.钢筋混凝土结构的温度场[J].工程力学,1996,13(1)：35-43.

[15]胡海涛.高温时高强混凝土压弯构件的试验研究及理论分析[D].西安:西安建筑科技大学，2002.

[16]徐玉野，吴波.高温下钢筋混凝土异形柱的截面特性[J].华南理工大学学报，2007，35(11):14-21.