一种改进的轨迹地图匹配算法

段宗涛，霍明生，康 军

(长安大学信息工程学院，陕西 西安 710064)

地图匹配是指将GPS点匹配到正确的道路上。在智能交通领域，交通流的预测及车辆的定位等方面都用到地图匹配，因此一个好的地图匹配算法是智能交通发展的有力保障。

根据输入数据所涉及信息的不同，目前的地图匹配算法[1]包括几何地图匹配算法、概率计算地图匹配算法、拓扑地图匹配算法和高级地图匹配算法。几何地图匹配算法相对简单易于实现，但是如果不使用GPS点之间的关系及道路之间的拓扑关系，匹配的准确度就会下降；概率计算地图匹配算法多涉及公式的推导且不容易理解，匹配效率也很低；拓扑匹配算法对于复杂的城市道路匹配效率不高；当采样频率较低且路网较为复杂的情况下，高级地图匹配算法具有很好的匹配准确率。

文献[2]中Newson等在2009年第一次提出了HMM(hidden Markov model)算法，虽然该算法对于时间间隔较大的数据具有很大的改善，但是没有考虑方向信息只考虑了距离信息。文献[3]提出了一种动态编程方法来识别每条路段，但试验结果表明该算法对于时间间隔较大的低频数据正确率较低。

本文提出一种基于HMM的改进的地图匹配算法。该地图匹配算法的设计过程为：首先建立候选路段集和路段拓扑关系集，然后介绍算法中轨迹点的方向概率、观测概率、状态转移概率及综合概率，最后介绍最短路径距离算法。

1 算法概述

本文数据采样间隔为30 s以上，图1为样本数据采样间隔分布图，可知该样本数据属于低频数据。目前针对低频采样数据的主要算法有HMMM、ST-Matching、IVMM等几种常见的全局算法[4]。本文充分考虑空间特征和几何拓扑结构，采用基于HMM改进的地图匹配算法进行验证。

1.1 路网拓扑构建

本文选择的路网数据为西安市城区的21 027条路段、16 907个节点，在建立拓扑关系集时分别对路段和节点进行编号。图2为西安市城区的路段和节点分布图。

图1 样本数据间隔分布

图2 西安市城区的路段和节点分布

由于每条路段都至少由两个节点构成，根据其首、末两个节点的经纬度坐标值计算每条路段的长度，根据计算结果可知，路段长度最小为1 m，最大为9186 m，根据路段节点、路段编号及路段的长度(距离权值)建立路网拓扑集，见表1。

表1 路网拓扑集

1.2 候选路段集构建

以当前轨迹点为圆心，选取半径r=200 m，可以最大限度地保证正确的候选路段落入该圆域内，同时候选路段集合也不至于过大。对每个轨迹点做一个候选圆域，只要落在该圆域内的路段就记作候选路段，如图3所示。

图3 候选路段计算示意图

由图3可知，O点表示轨迹点，落在圆域内的每个节点与轨迹点之间的地面距离为d，只要该地面距离小于等于200 m，该节点对应的路段就可以作为该轨迹点的候选路段，建立候选路段集。

这里给出地面距离的计算公式：

已知两点A(x1,y1)、B(x2,y2)，x1、x2表示A、B两点的经度，y1、y2表示A、B两点的纬度，利用弧长计算公式将经、纬度转化为弧长，计算公式如下

D=dis·π/180

(1)

式中，dis为经、纬度值；D为对应的弧长。

由式(1)可得

(2)

A、B两点间的地面距离公式为

(3)

式中，a=Y2-Y1；b=X2-X1；R为地球半径，取R=6 378 137 m。

1.3 投影坐标计算

如图4所示，P(X0,Y0)为轨迹点，O(X2,Y2)、O′(X1,Y1)为候选路段的首、末节点，Pe(Xe,Ye)为投影坐标，则投影点坐标[5]计算公式如下：

图4 投影示意图

OO′的直线方程为

Y-Y1=k(X-X1)

(4)

PPe所在的直线方程为

(5)

P到OO′的垂直距离，即PPe的长度为

(6)

投影坐标(Xe,Ye)为

(7)

(8)

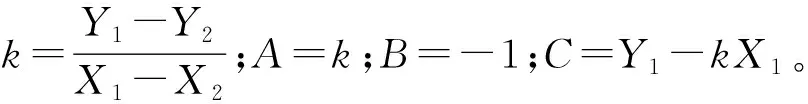
1.4 轨迹夹角θ的计算

如图5所示，轨迹点坐标为(x,y)，将轨迹点行驶方向与正北方向顺时针旋转的夹角记为φ，Si为轨迹点的候选路段[6]，将Si与正北方向的顺时针旋转夹角记为θ。

图5 轨迹夹角示意图

A(Xa,Ya)、B(Xb,Yb)为候选路段Si上的首、末节点，候选路段Si的行驶夹角θ的计算公式为

(9)

2 改进算法分析

2.1 问题描述

轨迹匹配问题是给定未加工的GPS轨迹Z和路网G(V,E)，从G中寻找路径可以从起始点达到指定点的过程。

给定GPS点的集合Z={z1,z2,…,zn}，每个GPS点包含经纬度和时间戳等信息。

每条路段e是一个有向边，分别具有e.id，长度e.l，起始点e.start，结束点e.end和中间点。

路网是一个有向图G(V,E)，V是顶点集合，代表路口或道路中的转折点，E是一系列有向边，代表路网中的路段。

2.2 算法描述

假设每一个GPS轨迹点为zt，t=1,2,…，n，轨迹点的每个候选路段为ri，i=1,2,…，n。

本文使用基于HMM的改进的地图匹配算法，首先加入一个方向概率作为路段在匹配过程中的一个指标，其次将观测概率以比值关系定义，最后将转移概率简化为实际地面距离与路径距离的一个比值。该算法的描述如下：

基于改进的HMM算法描述

输入：轨迹点zt、路网数据G(V,E)

输出：轨迹点zt的综合概率的max(P)

1. set the candidate radiusr=200 m

2. calculatezt→node of each road less than 200 m

3. get the candidate roadri

4. calculatext,i,θ,φ,ω,dt,Nω,p(zt|ri,p(xt,i→xt+1,j)

5. getPof each candidate road

6. get max(P) of eachzt

7. return max(P)

方向概率的计算公式为

(10)

观测概率[8]的计算公式为

(11)

由式(11)可知，GPS轨迹点与候选路段的地面距离越近，该路段的观测概率就会越大；反之，距离越远，观测概率就越小。因此，距离越小的候选路段最有可能是其真正的候选路段。

转移概率计算公式如下

(12)

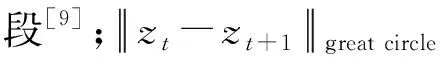
根据式(10)、式(11)、式(12)定义综合概率为

P=Nωp(dt)p(xt,i→xt+1,j)

(13)

利用式(13)计算轨迹点的max(P)，过程如图6所示。

图6 匹配过程

利用本文提出的改进算法并行计算轨迹点的最大P，最后对整个轨迹点进行汇总，得到一个计算值最大的匹配点的序列形成匹配路径。

2.3 最短路径算法[10]描述

在式(12)中求解相邻两个轨迹点xt,i和xt+1,j(i=1,2，…，m,j=1,2，…，n)的最短路径route距离[11]时，采用基于广度优先搜索和优先队列的Dijkstra算法，由于在每次求解时都会进行m·n次运算才可得到route值，为了减少时间复杂度，采用矩形和椭圆限制搜索区域[12]进行改进。

基于Dijkstra算法的矩形和椭圆限制搜索区域过程

输入：xt,i→xt+1,j，矩形搜索区域G(V,E)

输出：xt,i→xt+1,j的最短路径距离d[v]

1. fuction Dijkstra(G,w,s)∥w表示路径长度

2. for each vertex inV

3.d[v]=infinity

4. previous[v]=undefined

5.d[s]=0

6.Sis empty set

7.Qis a set of all vertexs

8. whileQis not an empty set

9.u=Get min(Q)

10.S.add(u)

11. for each edge outgoing from u as (u,v)

12. ifd[v]>d[u]+w(u,v)

13.d[v]=d[u]+w(u,v)

14. previous[v]=u

15. end if

16. returnd[v]

3 试验结果和分析

本文试验所用的数据包含地图数据[13]及西安市出租车数据，采样间隔为30 s以上。GPS轨迹数据格式包括车牌号码、GPS时间、经度、纬度、速度、方向角、浮动车状态。为了验证本文算法，首先测试了文献[2]中Newson等提出的传统的HMM算法，测试的准确率在86.4%。而采用本文改进的算法进行测试，匹配准确率可以达到94%以上，具有很好的匹配效果。

表2为轨迹点匹配前和匹配后的部分结果对比[14]。

表2 轨迹点坐标匹配前后对比

图7为部分轨迹点匹配前的示意图，图8为部分轨迹点匹配后的示意图。

图7 匹配前

图8 匹配后

使用传统的HMM地图匹配算法[2]和改进的HMM地图匹配算法的准确率比较见表3。

表3 算法准确率比较 (%)

4 结 语

本文使用基于HMM的改进的地图匹配算法，建立路网拓扑集[15]，对轨迹点建立候选路段集，计算轨迹点候选路段的概率，选取最大概率值对应的路段为最佳的匹配路段。利用本文提出的算法可以达到很好的匹配效果，未来可以在计算最短路径距离和候选路段选取方面进行优化。

参考文献：

[1] 高文超，李国良，塔娜.轨迹路网匹配算法综述[J].软件学报，2018,29(2)：225-250.

[2] NEWSON P，KRUMM J.Hidden Markov Map Matching Through Noise and Sparseness[J].ACM GIS，2009，9(11)：336-343.

[3] CHEN B Y，YUAN H，LI Q，et al.Map Matching Algorithm for Large-scale Low-frequency Floating Car Data[J].International Journal of Geographical Information Science，2014，28(1)：22-38.

[4] YUAN J，ZHENG Y，ZHANG C，et al.An Interactive-voting Based Map Matching Algorithm[J].Mobile Data Management，2010，11(10)：43-52.

[5] 李殿茜，王翌，刘垒，等.一种地图匹配算法的设计与实现[J].导航定时，2017，4(2)：31-34.

[6] 陈锋.一种改进的点到线的地图匹配算法[J].内蒙古科技与经济，2004，4(4)：74-76.

[7] KRUMM J.A Markov Model for Driver Turn Prediction[J].Society of Automotive Engineers，2008，22(1)：1-25.

[8] ZELENKOV A V.Calculation of Parameters of Hidden Markov Models Used in the Navigation Systems of Surface Transportation for Map Matching:A Review[J].Automatic Control and Computer Sciences，2010，44(6)：309-323.

[9] SZWED P，PEKALA K.An Incremental Mapmatching Algorithm Based on HMM [J].International Conference on Artifical Intelligence and Soft Computing，2014，13(2)：579-590.

[10] QUDDUS M，WSHINGTON S.Shortest Path and Vehicle Trajectory Aided Map-matching for Low Frequency GPS Data[J].Transportation Research Part C，2015，2(17)：328-339.

[11] 姜雪原.基于动态规划算法的轨迹地图匹配软件设计与实现[J].软件，2015，36(5)：108-112.

[12] 陆峰，卢东梅，崔伟宏.交通网络限制搜索区域时间最短路径算法[J].中国图象图形学报，1999，4(10)：849-853.

[13] 高强，张凤荔，王瑞锦，等.轨迹大数据：数据处理关键技术研究综述[J].软件学报，2017，28(4)：959-992.

[14] 吴刚，邱煜晶，王国仁，等.基于隐马尔科夫模型和遗传算法的地图匹配算法[J].东北大学学报(自然科学版)， 2017，38(4)：472-475.

[15] 王晓蒙，池天河，林晖，等.一种面向海量浮动车数据的地图匹配算法方法[J].地球信息科学，2015，17(10)：1143-1150.