局部相位相关法在密集匹配中的应用及精度分析

邹进贵，杨义辉，李 琴，翟若明

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学精密工程与工业测量国家测绘地理信息局重点实验室，湖北 武汉 430079； 3. 辽宁省交通高等专科学校，辽宁 沈阳 110122)

在基于双目视觉的密集匹配方法中，基于全局和基于区域的立体匹配算法都可以输出稠密视差图，但传统匹配算法对于含有显著图像噪声及光照变化的立体像对匹配效果较差，容易出现误匹配现象[1-2]。

而基于频域的相位相关算法(phase only correlation，POC)是一种基于傅里叶(Fourier)功率谱的频域相关算法，由于该方法只取互功率谱中的相位信息，因而减少了对图像内容的依赖性，而且所获得的相关峰尖锐突出。因此该算法块位移量检测范围较大，有较高的匹配精度。另外，POC算法对图像灰度依赖较小，具有一定的抗干扰能力，因此经常用于图像的配准处理中。但由于该方法计算量大、对窗口形状和大小要求严格，在密集匹配中运用较少[3-5]。

图像配准是将同一场景的两幅或多幅图像重叠在一起，从几何学来讲就是建立待配准图像和模板图像之间的对应变换关系[3]。如果以立体像对中同一位置的某点为中心进行加窗Fourier变换，即局部采样矩阵Fourier变换，再利用局部相位相关，就可以精确定位相位互相关谱的峰值，进而估计出窗口间亚像素级平移参数。通过对图像中每个像素点进行上述计算，取各点横向平移参数，即为该点视差值，进而得到视差图。

1 相位相关法的密集匹配原理

由Fourier变换的性质可知，在时域中信号的平移运动可以通过在频域中相位的变化表现出来，且这种平移在频域中只反映在相位变化上，而对应的幅度谱是相同的。

1.1 窗口二维傅里叶变换

若尺寸为M×N的图像的函数表达为f(x,y)，则其二维离散Fourier变换为

(1)

其反变换为

(2)

采用一定长宽的矩形窗对立体像对同一位置进行加窗Fourier变换，即可得到该点附近的频域相位谱，将其定义为局部相位

(3)

式中，Im(u,v)和Re(u,v)分别为Fourier变换所得复数矩阵的虚部和实部，这里相位取[-π,π)的主值区间。

1.2 相位相关法

相位相关主要基于Fourier变换中的平移定理。假设fL(x,y)和fR(x,y)分别为左图像和右图像的窗口信号，且满足

fR(x,y)=fL(x-dx,y-dy)

(4)

式中，dx和dy分别为窗口信号在横向和纵向上的位移量。若它们对应的Fourier变换分别为FL(u,v)和FR(u,v)，可以得到

FR(u,v)=e-j 2π(udx+vdy)FL(u,v)

(5)

定义这两幅图像间的互相关功率谱为[6 -7]

(6)

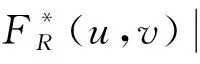
此外，相位相关法对像对间的角度变化十分敏感，通过基于Fourier-Mellin变换的相位相关法同样可以获得图像间的旋转角度及位移量的估值[8]。本文仅考虑无上下视差的核线影像间的情况，即通过基本矩阵来获得同名核线并将其覆盖的像素“取出”重新进行排列，以完成核线重采样。

1.3 视差计算与视差图输出

如果立体像对经过核线重采样，已消除同一水平线上的上下视差dy，则只需要取水平偏移量dx，即为左、右图像在该点的视差值。

图1 互功率谱逆变换所得的相关函数峰值

本文采用快速二维傅里叶变换算法(FFT)，取窗口大小为2的整数次幂，得到窗口频域复矩阵后，再利用相位相关法进行窗口块位移量估计，即相位相关函数峰值所在位置，如图2、图3所示。

图2 图像整体的相位相关函数

图3 图像窗口的相位相关函数(64×64)

取横向位移值输入视差矩阵，进而得到视差图。算法的整体流程如图4所示。算法流程中相关函数的合理性判断环节是对视差值的定性约束和修正，即当计算所得的相位相关函数不具有脉冲特性或超过图像整体偏移量5倍时，说明窗口选择存在问题，此时可以通过扩大窗口尺寸重新进行块位移量计算。

图4 局部相位相关法的密集匹配流程

2 试验结果与分析

2.1 不同窗口尺度的立体匹配试验

本文选取了不同尺度的矩形窗口进行基于局部相位相关法的密集匹配试验，使用FFT算法时，窗口长宽必须为2的整数次幂，而窗口过小或过大都会导致计算出的视差值出现错误。因此综合经验值，选取了16、32和64三种尺寸共9种组合的矩形窗。

利用经过核线重采样后的两组标准立体像对(由www.middlebury.edu/stereo/获取)，按照图4流程进行不同窗口的匹配试验。其中对试验1加入了均值为0、方差为20的高斯白噪声，试验2加入了10%的椒盐噪声，所得噪声条件下的密集匹配的视差结果如图5—图8所示。

图5 试验1立体匹配原图、加入随机噪声原图及理想视差图

图6 试验1视差图结果((a)—(i)为选择不同尺寸的矩形窗口)

图7 试验2立体匹配原图、加入椒盐噪声原图及理想视差图

图8 试验2结果((a)—(i)为选择不同尺寸的矩形窗口)

2.2 匹配结果分析

将试验所得的视差图进行线性拉伸变换，再与理想视差图作差，可以得到立体像对的误匹配率，见表1。

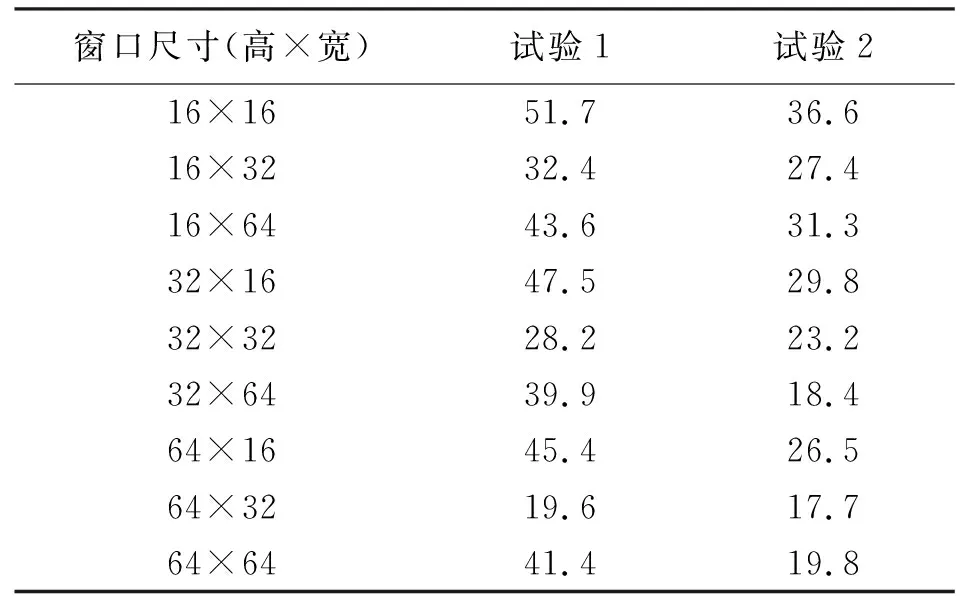
表1 不同尺寸窗口的误匹配率 (%)

由表1可知，不同尺寸窗口的匹配结果相差较大，其中大小为64×32的局部相位相关法匹配效果最好，得到的视差图最接近理想视差图。其中对于加入的高斯白噪声，在进行窗口FFT时可以通过低通滤波来剔除，而对于椒盐噪声，则是采用窗口中值滤波进行平滑处理，因此该算法的抗噪性和稳健性得到了提高。

为进行对比分析，在考虑同等算法复杂度的情况下，采用5×5窗口大小的基于SSD(像素点灰度差的平方和)准则的区域立体匹配算法进行密集匹配，两组试验所得误匹配率分别为27.1%和17.6%，而基于灰度差绝对值和(SAD)准则的区域立体匹配算法所得误匹配率分别为24.4%和19.3%。本文两组试验的匹配正确率均可达80%以上，验证了基于局部相位相关法的立体匹配算法的可行性和有效性。

此外，相比其他立体匹配算法，该算法进行局部视差估计时，不需要初值进行迭代计算，而能够直接得到视差值。因此在算法效率上要优于基于区域的立体匹配算法。

由于立体像对中图像的灰度和纹理特征变化不一，在视差变化较大的边缘和细节处，较小的窗口可以得到更为准确的视差值，而对于视差变化较小且灰度变化不大的区域，大窗口得到的视差值更准确。因此如何针对不同特征区域选择大小可以自适应的窗口进行视差估计，仍需要进一步研究。

3 结 语

本文基于局部相位相关算法，利用窗口傅里叶变换，对双目立体像对进行视差值估计，进而得到密集匹配视差图。结果表明，在选择合适尺度的窗口下，基于局部相位相关的立体匹配算法能够有效地得到密集视差图，且相对其他传统的立体匹配算法，该算法能够有效地减弱噪声、光照等影响，且算法效率较高，对基于双目视觉的三维立体建模提供一定的方法借鉴。但该算法受图像窗口的形状和大小影响较大，因此对窗口尺寸的选择还需要进一步优化。

参考文献：

[1] 刘盛夏.基于相位信息的立体图像匹配研究[D].上海:上海交通大学,2010.

[2] 郭龙源.计算机视觉立体匹配相关理论与算法研究[D].南京:南京理工大学,2009.

[3] 吴四夫,付宇卓,邓红梅.基于相位相关算法的实时图像匹配系统[J].计算机仿真,2005，22(11):84-86.

[4] 郑志彬,叶中付.基于相位相关的图像配准算法[J].数据采集与处理，2006,21(4):444-449.

[5] 王彩玲,程勇,赵春霞,等.局部相位相关用于图像亚像素级配准技术研究[J].中国图象图形学报,2011,16(3):427-432.

[6] KOBAYASHI K,NAKAJIMA H,AOKI T,et al.Principals of Phase Only Correlation and Applications[J].ITE Technical Report,1996，20(41):2-4.

[7] WENG J.Image Matching Using the Windowed Fourier Phase[J].International Journal of Computer Vision，1993,11(3):211-236.

[8] 吴军,姚泽鑫,程门门.融合SIFT与SGM的倾斜航空影像密集匹配[J].遥感学报,2015，19(3):431-440.

[9] 孙汉昌,武毅,高峰,等.基于分形理论和相关匹配的快速目标检测技术[J].测绘通报，2014(S0):159-162.

[10] REDDY B S，CHATTERJI B N.An FFT-based Technique for Translation,Rotation,and Scale-invariant Image Registration[J].IEEE Transactions on Image Processing，1996,5(8):1266-1271.

[11] 郭龙源,孙长银,张国云,等.基于相位一致性的可变窗口立体匹配算法[J].计算机科学，2015,42(6A):13-15.

[12] 王瑞瑞,冯伍法,张艳,等.一种结合相位相关法和AKAZE算法的纹理缺乏地区影像匹配技术[J].测绘通报,2017(4):49-52.

[13] 章毓晋.图像处理和分析[M].北京:清华大学出版社,1999.

[14] 彭诚,孙新柱.一种改进的深度图像修复算法研究[J].重庆工商大学学报(自然科学版)，2016，33(1):65-69.

[15] 沈萍萍,余勤.基于离散余弦变换的非局部均值图像去噪算法[J].计算机工程与设计,2017,38(1):183-186.

[16] 王阳.高密度椒盐噪声污染图像修复方法研究[D].大连:大连理工大学,2016.