来流导致的高超声速气动热不确定度量化分析
2018-06-04张伟王小永于剑阎超
张伟, 王小永, 于剑, 阎超
(北京航空航天大学 航空科学与工程学院, 北京 100083)
随着计算机技术和数值计算方法的发展,计算流体力学[1]在工程中起到了越来越重要的作用。目前大部分的数值模拟都是确定性的,即在计算中需要给出确定的来流条件、几何尺寸、边界条件以及精确的物理模型。然而高度复杂的航天飞行器的分析和设计中不确定性因素是普遍存在的,例如几何模型在载荷作用下的变形和大气来流条件变化等。不确定性因素可分为偶然不确定度(aleatory uncertainty)和认知不确定度(epistemic uncertainty)两大类[2]。偶然不确定度是由于事物固有的随机性导致的不确定度;而认知不确定度是由于缺乏理论知识导致的不确定度。不确定度量化(uncertainty quantification)分析对复杂航天系统的鲁棒设计和可靠性分析是非常重要的,并对飞船返回舱的热防护系统(Thermal Protection System,TPS)设计具有重要参考意义[3]。
飞船返回舱在再入大气层过程中飞行高度逐渐降低,大气来流等条件也在不断发生变化。Champion[4]的研究表明高度为48~69 km的大气密度波动约为5%。因此为得到可靠的气动热数值预测,必须考虑来流参数的不确定性和由此带来的气动热预测的不确定度。目前已经发展出很多不确定度量化方法,如已经在工程中应用较多的蒙特卡罗(Monte Carlo)方法[5-6],这种方法的主要缺陷是需要大量样本,对计算资源消耗较大。近年来,采用多项式混沌(Polynomial Chaos,PC)方法在CFD不确定分析得到了广泛应用。多项式混沌方法又可分为嵌入式和非嵌入式[7]。本文采用的是非嵌入式多项式混沌(Non-Intrusive Polynomial Chaos,NIPC)方法,即选择一组正交多项式作为空间的无限基函数,将变量分解为确定和随机两部分从而构造出多项式混沌展开式。该方法相比于嵌入式多项式混沌方法只需把CFD求解器当做黑盒子,基于确定性的解来近似多项式混沌展开式的系数。在NIPC方法的基础上,可采用Sobol指数来衡量输入变量的敏感性。
目前,NIPC方法被广泛应用到CFD不确定性分析中。Hosder等[7-8]将NIPC方法应用于求解楔角变化的随机斜激波问题和来流马赫数与迎角变化的三维NACA65A004机翼气动力问题,研究了单个随机输入变量和多维不确定性输入变量的情况,结果表明NIPC方法具有较高的效率和准确性。Loeven和Bijl[9]开展了NACA5412翼型数值模拟的几何不确定度量化分析,研究了翼型最大弯度、最大弯度弦向位置以及厚度3个不确定性因素对升力系数的影响。Weaver和Alexeenko[10]对FIRE2飞行器进行了高超声速数值模拟,研究了来流速度、来流密度、碰撞系数和来流温度对气动热和流场的影响。Bettis和Hosder[2]对高超声速再入流动的不确定度问题进行了分析,研究混合不确定性输入变量对气动热的影响。相比于国外,国内类似的工作还未开展,相关的研究还未见公开文献报道。
本文以Apollo飞船返回舱为研究对象开展气动热数值预测,选取了来流速度、来流温度、壁面温度和来流密度4个不确定性输入变量,其中来流速度变化范围为±120 m/s(±2%),来流温度、壁面温度和来流密度变化范围为±10%,利用NIPC方法对气动热进行不确定度量化和敏感性分析,为飞船返回舱气动热防护设计提供参考依据,进一步用于高超声速飞行器的鲁棒优化设计和可靠性分析。
1 计算方法
1.1 控制方程
采用有限体积法求解层流Navier-Stokes方程组,曲线坐标系(τ,ξ,η,ζ)下,三维无量纲守恒形式的热化学非平衡控制方程为
(1)
(2)
S=1/J(ωi,0,0,0,0,Sv)
(3)
1.2 离散方法
时间离散采用隐式LUSGS方法;无黏通量空间离散采用Roe格式,二阶MUSCL重构,采用minmod限制器;黏性通量离散采用二阶中心格式。
1.3 物理模型
真实气体效应计算过程中单一组分的黏性系数、平动温度热传导系数和振动温度热传导系数分别由Blotter曲线拟合和Eucken关系式计算。混合气体的黏性系数、热传导系数由Wilke半经验公式计算。
1.4 化学反应模型
化学非平衡源项主要反应了组分间化学反应的影响。根据组分选取的不同,空气的化学反应模型一般分为2、5、7和11组分化学反应模型。对于ns个组分的混合气体,设化学反应总数为nr,其化学反应方程为如下通式[12]:
(4)
式中:Xi为单位体积摩尔数的化学组分或催化体,Xi=ρi/Mi,Mi为气体组分的摩尔质量,αr和βr分别为化学反应式中反应物和生成物的计量系数。
则ωi具体形式为
(5)
整理后源项表达式为
(6)
1.5 不确定度分析方法
NIPC方法主要基于混沌多项式展开(Polynomial Chaos Expansions,PCE)理论,具有坚实的数学基础,是一种非常有效的基于随机展开的不确定度分析方法。PCE方法的一个重要特性是可以将任一随机变量分解为确定和随机2个独立部分。在不确定性的流体力学问题中,任意随机变量α*(如压力、温度和壁面热流等)可以表示为
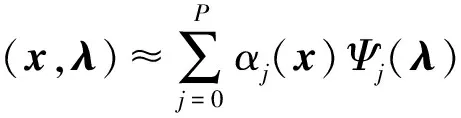
(7)
式中:αj(x)为确定部分的耦合系数;Ψj(λ)为以n维随机变量λ=(λ1,λ2,…,λn)为自变量的j阶随机基函数。
在式(7)中,Ψj(λ)的项数是无穷的,出于计算量的考虑,PCE模型通常在某阶p被截断。相应地,p阶PCE模型的项数可以表示为阶数p和随机变量的维数n的函数[13]为
(8)
根据随机输入参数的分布类型,需要选取不同的多项式基函数。当输入参数服从正态分布时选取Hermite正交多项式基函数;当输入参数服从均匀分布时选取Legendre正交多项式基函数。
目前,主要有2种形式的基于非嵌入式混沌多项式的不确定度分析方法:随机响应面法(Stochastic Response Surface Method,SRSM)和基于Galerkin投影法。本文采用随机响应面法来求解PCE系数,基本流程如图1所示。
为了计算PCE模型中的未知PCE系数αj(j=0,1,…,P),首先需要选取有效的样本点,这里将回归中用到的样本点数表示为N。通常采用过采样(over sampling)策略,文献[8]中推荐用两倍于未知PCE系数个数的样本(即N=2Nt=2(P+1))可以得到比较满意的结果。采用最小二次回归来求解PCE系数,将样本λ=[λ1,λ2,…,λj,λj+1,…,λN]T和相应的函数响应值G=[g(X1),g(X2),…,g(XN)]T分别代入到PCE模型右端和左端得
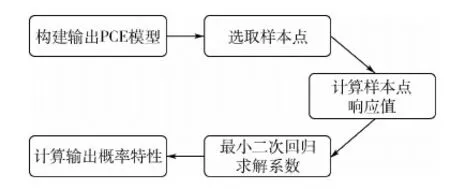
图1 不确定度分析方法流程Fig.1 Flowchart of uncertainty analysis method
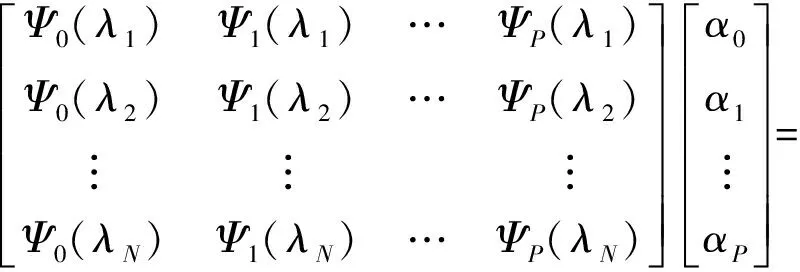
(9)
可以简写为
Aα=G
定义:
(10)

利用线性最小二次回归,使K(αj)最小,可以求得PCE系数为
(11)
敏感性是表征随机物理问题中每个输入变量对输出变量不确定度的相对贡献大小。基于方差的Sobol分解方法可以用于敏感性分析,PCE系数确定之后,Sobol指数可以通过以下推导获得,输出变量总方差可以表示为[14]
(12)
总方差可以分解为
(13)
部分方差表示为
(14)
Sobol指数定义为
(15)
输入变量i的Sobol指数(STi)定义为包含变量i的所有部分Sobol指数的和,即
Li={(i1,i2,…,is):∃k,1≤k≤s,ik=i}
(16)
2 算例验证与结果分析
2.1 算例验证
本文首先选取ELECTRE标模[15]对本文的热化学非平衡程序进行验证。ELECTRE球锥标模几何外型如图2(a)所示。来流速度u∞=4 230 m/s (Ma=12.9),来流密度ρ∞=6.944×10-4kg/m3,来流温度T∞=265 K,空气质量分数组成为YN=0.77,YO=0.23,YN和YO分别为N2和O2的质量分数,采用双温度热力学模型和Park的11组分21反应化学反应动力学模型,壁面为等温壁(Tw=343 K),并且设为完全催化壁。网格示意图如图2(b)所示,网格数为80×90,第一层网格法向间距取为1×10-5m。
图3为本文程序的热流计算结果与飞行试验的对比。计算结果与飞行试验数据相吻合。在头部驻点区域,本文程序计算的热流与Fay-Riddell热流公式的结果吻合,当略高于飞行试验结果。产生差异的原因是在实际飞行条件下ELECTRE标模的热防护设备减小了壁面催化效果[16]。
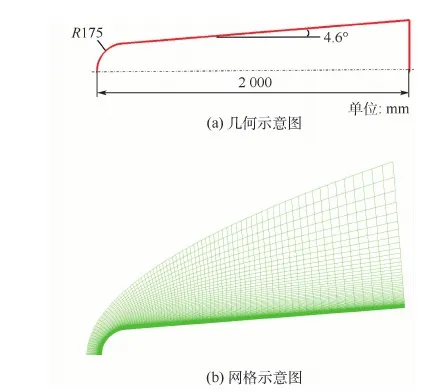
图2 ELECTRE标模几何与网格示意图Fig.2 Schematic of geometry and computational mesh of ELECTRE vehicle
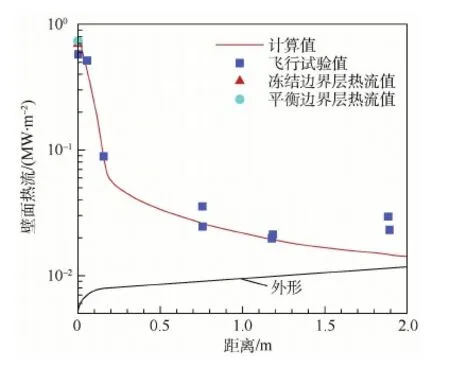
图3 ELECTRE标模壁面热流分布Fig.3 Heat flux distribution on wall surface of ELECTRE vehicle
图4对比了本文与文献[15]中ELECTRE标模的驻点线温度分布。由图4可知,本文程序的计算结果与文献[15]的计算结果相吻合,图中T为平动温度,Tv为振动温度。
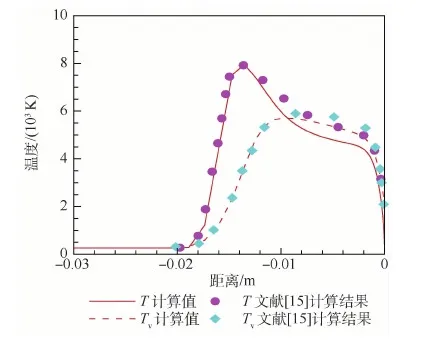
图4 ELECTRE标模驻点线温度分布Fig.4 Temperature distribution along stagnation line of ELECTRE vehicle
2.2 结果分析
2.2.1 网格无关性验证与基准状态分析
计算模型为钝头体的Apollo飞船返回舱前体[15],Apollo飞船返回舱几何外型如图5(a)所示,基准状态流动条件如表1所示。计算中采用双温度热力学模型,选用Park的11组分21反应化学反应动力学模型。壁面温度取为800 K,并且设为非催化壁面条件。网格如图5(b)所示,第一层网格高度为2×10-4m。
为了保证计算在一定网格密度下不受网格数量的影响,本文选取了3个水平的网格数量来开展网格无关性研究:A(100×140),B(75×110),C(50×80)。图6给出了3个网格水平下壁面热流结果对比。可以看出网格A与网格B结果非常接近,而网格C与其有一定区别,故网格B已经可以满足网格无关性要求,本文采用网格B(75×110)计算。
图7为基准状态下平动温度和压力的等值线图,图8为平动温度及振动温度沿驻点线变化。激波过后,平动温度首先被激发而升高。随后平动能和振动能之间产生能量松弛过程,振动温度也随之增加。一段距离后,平动温度和振动温度达到平衡。
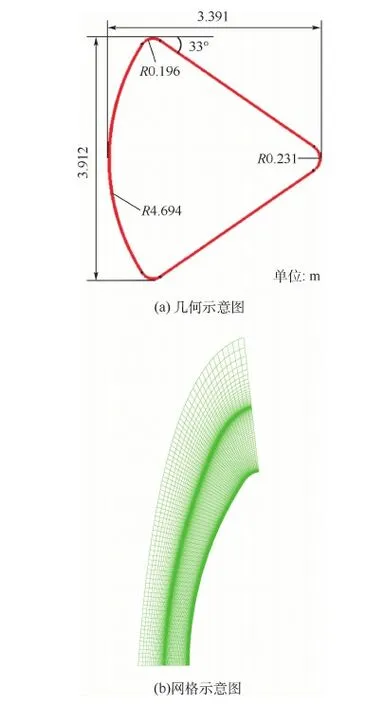
图5 Apollo返回舱几何与网格示意图Fig.5 Schematic of geometry and computational mesh of Apollo returning capsule

参 数高度/kmu∞/(m·s-1)T∞/Kρ∞/(kg·m-3)YN/YO数 值67.360402259.8×10-50.77/0.23
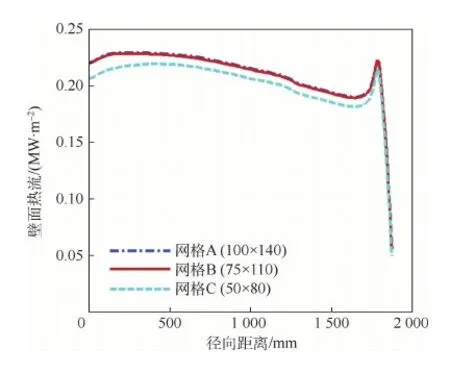
图6 不同网格水平下壁面热流对比Fig.6 Wall heat flux comparison under different grid levels
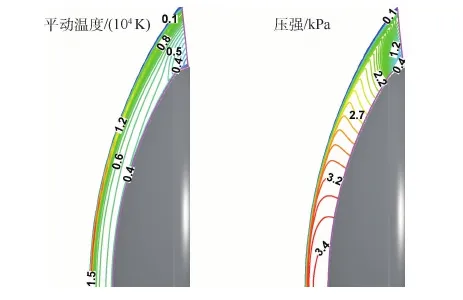
图7 基准状态平动温度与压力分布Fig.7 Translational temperature and pressure contours for baseline case
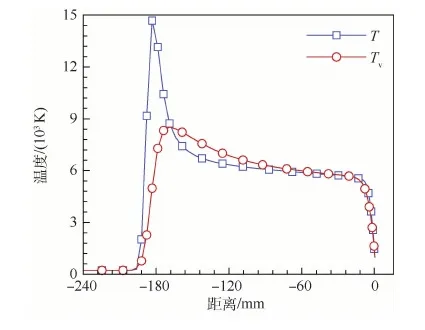
图8 Apollo返回舱驻点线温度分布Fig.8 Temperature distribution along stagnation line of Apollo returning capsule
2.2.2 不确定度量化
选取大气来流条件(来流速度、来流温度与来流密度)和边界条件(壁面温度)共4个变量作为随机输入来研究输出响应的不确定度传播和敏感性分析。4个变量的不确定度大小如表2所示,取值范围参考了文献[10],来流速度变化范围为±120 m/s(±2%),来流温度、壁面温度和来流密度变化范围为±10%,并假设均服从均匀分布。
PCE模型在二阶截断,由式(8)计算得到样本数为30,采用拉丁超立方(Latin Hypercube Design,LHD)[12]方法进行抽样。95%置信度条件下,定义输出响应壁面热流的不确定度为UQ%=100×1.96σR/μR。

表2 输入变量不确定度
图9为基准状态下的壁面热流和NIPC方法计算的壁面均值热流。壁面热流沿径向距离总体呈先减小后增大再减小的趋势,在驻点和肩部附近出现峰值,在肩部附近,曲率突然减小且膨胀波气流加速换热效应起主导作用,故其壁面热流较高。基准状态下壁面热流和NIPC方法计算的壁面均值热流在驻点处差异为3.2%,在肩部峰值处差异约为0.78%。
图10为相应的壁面热流不确定度和输入变量敏感性指数分布。壁面热流的不确定度沿径向距离先减小后增大再减小,在驻点和肩部存在峰值分别约为19.8%和17.3%,相应的热流不确定度区间大小分别约为0.087 MW/m2和0.076 MW/m2。
驻点和肩部热流密度的平均值、标准差、95%置信不确定区间和不确定度如表3所示。
不确定度量化结果表明,不确定性输入变量会引起壁面热流明显的变化,其不确定度范围约为15.9%~19.8%,并且在驻点(19.8%)和肩部(17.3%)达到峰值。
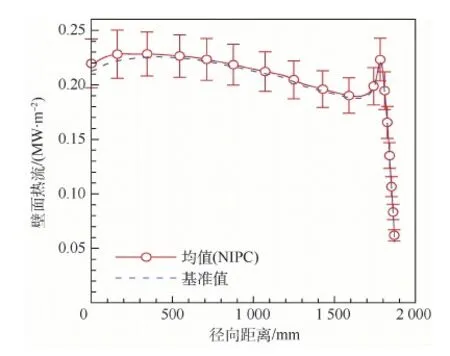
图9 壁面热流对比Fig.9 Wall heat flux comparison
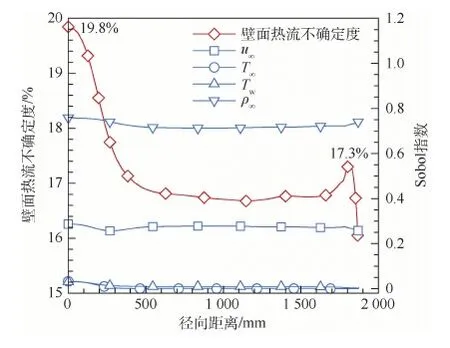
图10 壁面热流不确定度和输入变量Sobol指数分布Fig.10 Uncertainty of wall heat flux and Sobol index distribution of input variable

量化结果驻点SR=0肩部SR=1817mm平均值μR/(MW·m-2)0.22010.2230标准差σR/(MW·m-2)0.02230.01952-σ区间(0.1764,0.2638)(0.1848,0.2612)不确定度/%19.817.3
2.2.3 敏感性分析
各输入变量的Sobol指数沿径向距离变化如图9所示,在来流速度、来流温度、壁面温度和来流密度4个不确定性变量中,各变量的Sobol指数在驻点处稍大,沿径向距离变化较为平缓,故各变量对不同位置的壁面热流影响规律较为一致。来流密度的不确定度对壁面热流变化贡献最大,其Sobol指数约为0.72。其次是来流速度,其Sobol指数约为0.27。相比而言壁面热流几乎不受来流温度和壁面温度影响。
驻点和肩部各输入变量的Sobol指数如表4所示。
各输入不确定度对输出不确定度相对贡献如图11所示。在驻点处,来流密度和来流速度对壁面热流不确定度贡献分别为62.29%和23.56%,相应的不确定度和不确定度区间大小分别为12.3%、4.8%和0.054、0.02 MW/m2。在肩部,来流密度和来流速度对壁面热流不确定度贡献分别为72.76%和26.74%,相应的不确定度和不确定度区间大小分别为12.6%、4.7%和0.056、0.02 MW/m2。来流温度、壁面温度及其他交互影响项几乎不对壁面热流变化起作用。
敏感性分析表明,在高超声速飞行器气动热数值模拟和试验中,需要重点关注来流密度和来流速度的变化。来流密度变化(10%)和来流速度变化(2%)对壁面热流的不确定度贡献最大分别约为70%和25%,引起的不确定度分别约为12%和5%,故来流密度和来流速度的变化会对气动热数值预测产生不可忽略甚至明显的影响,而来流温度和壁面温度几乎不产生影响。
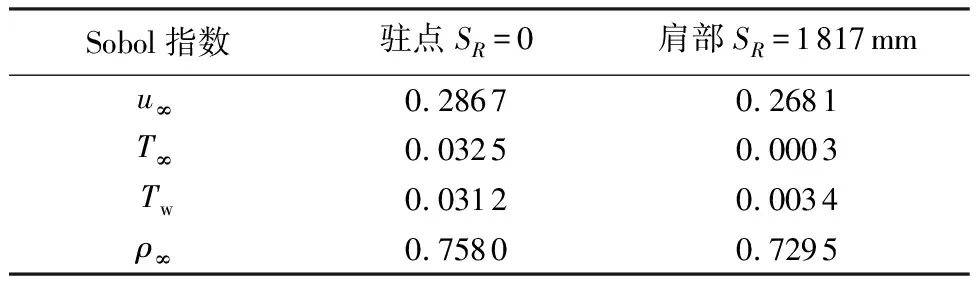
表4 驻点和肩部各输入变量Sobol指数
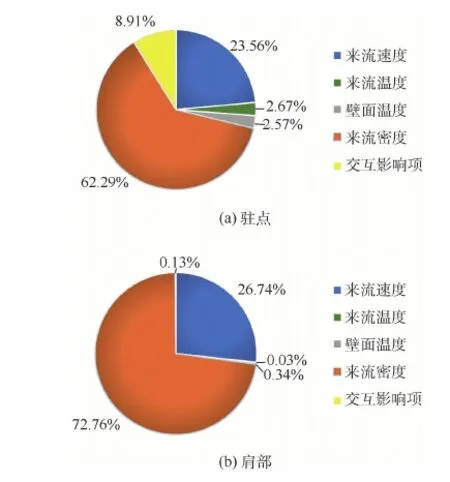
图11 驻点和肩部各输入变量对总体不确定度的相对贡献Fig.11 Relative importance of each input variable on overall uncertainty at stagnation and shoulder
3 结 论
本文对高超声速地球再入飞行器进行了热化学非平衡气动热数值预测,选取了来流速度、来流温度、壁面温度和来流密度4个不确定性输入变量,其中来流速度变化范围为±120 m/s(±2%),来流温度、壁面温度和来流密度变化范围为±10%,采用非嵌入式多项式混沌(NIPC)方法对气动热进行了不确定度量化分析和敏感性分析,得到的结论如下:
1) ELECTRE标模热流计算结果与飞行试验值相吻合,表明热化学非平衡计算程序具有较高的气动热预测精度。Apollo飞船返回舱再入时由于高温高马赫数,流场表现出典型的热化学非平衡特性,壁面热流在驻点和肩部附近存在峰值。
2) 采用基于NIPC方法的不确定性分析方法,得到了壁面各点热流的均值、标准差和不确定度。来流条件的变化会引起壁面热流明显变化,壁面热流的不确定度沿壁面先减小后增大再减小,在驻点和肩部存在2个峰值,其不确定度和不确定度区间大小分别约为19.8%、17.3%和0.087、0.076 MW/m2。
3) 采用基于Sobol指数的敏感性方法,对计算结果进行了敏感性分析。各变量对不同位置的壁面热流影响规律一致,来流密度变化和来流速度变化对热流不确定度贡献最大,而来流温度变化和壁面温度变化几乎不产生影响,在高超声速气动热预测中应重点关注来流密度和来流速度的变化。
4) 不确定度量化和敏感性分析对数值模拟可信度评估有重要意义,为高超声速气动热数值预测提供了可靠的参考,可进一步用于高超声速飞行器的鲁棒性优化设计和可靠性分析。后续工作将对热化学非平衡数值模拟中的化学反应模型进行不确定度分析。
参考文献 (References)
[1] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社:2006:2-6.
YAN C.Computational fluid dynamic’s methods and applications[M].Beijing:Beihang University Press,2006:2-6(in Chinese).
[2] BETTIS B,HOSDER S.Uncertainty quantification in hypersonic reentry flows due to aleatory and epistemic uncertainties[C]∥49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston:AIAA,2011.
[3] BRUNE A J,WEST T K,HOSDER S,et al.A review of uncertainty analysis for hypersonic inflatable aerodynamic decelerator design[C]∥21st AIAA International Space Planes and Hypersonics Technologies Conference.Reston:AIAA,2017:2373.
[4] CHAMPION K S W.Middle atmosphere density data and comparison with models[J].Advances in Space Research,1990,10(6):17-26.
[5] ECKHARDT R.Stan Ulam,John Von Neumann,and the Monte Carlo method[J].Los Alamos Science Special Issue,1987(15Special):131-137.
[6] ZAREMBA S K.The mathematical basis of Monte Carlo and quasi-Monte Carlo methods[J].SIAM Review,1968,10(3):303-314.
[7] HOSDER S,WALTERS R,PEREZ R.A non-intrusive polynomial chaos method for uncertainty propagation in CFD simulations[C]∥44th AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA,2006:891.
[8] HOSDER S,WALTERS R,BALCH M.Efficient sampling for non-intrusive polynomial chaos applications with multiple uncertain input variables[C]∥Non-Deterministic Approaches Conference.Reston:AIAA,2007:1939.
[9] LOEVEN A,BIJL H.Airfoil analysis with uncertain geometry using the probabilistic collocation method[C]∥49th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2008:2070.
[10] WEAVER A B,ALEXEENKO A.Flowfield uncertainty analysis for hypersonic CFD simulations[C]∥48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston:AIAA,2010:1180.
[11] 周禹.高超声速热化学非平衡流场数值模拟研究[D].北京:北京航空航天大学,2009:13-19.
ZHOU Y.Numerical simulation of hypersonic thermal and chemical nonequilibrium flows[D].Beijing:Beihang University,2009:13-19(in Chinese).
[12] WANG X,YAN C,ZHENG W L,et al.Laminar and turbulent heating predictions for mars entry vehicles[J].Acta Astronautica,2016,128:217-228.
[13] 熊芬芬,杨树兴,刘宇,等.工程概率不确定性分析方法[M].北京:科学出版社,2015:115-117.
XIONG F F,YANG S X,LIU Y,et al.Engineering probability uncertainty analysis method[M].Beijing:Science Press,2015:115-117(in Chinese).
[14] SOBOL I M.Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics & Computers in Simulation,2001,55(1-3):271-280.
[15] MUYLAERT J,WALPOT L,HAUSER J.Standard model testing in the European high enthalpy facility F4 and extrapolation to flight[C]∥Joint Propulsion Conference and Exhibit.Reston:AIAA,1992:S396.
[16] HAO J A,WANG J Y,LI C H.Numerical study of hypersonic flows over reentry configurations with different chemical nonequilibrium models[J].Acta Astronautica,2016,126:1-10.
