生物效应大数据评估聚类算法的并行优化

彭绍亮，杨顺云，孙哲，程敏霞，崔英博，王晓伟，李非，伯晓晨，廖湘科

1. 湖南大学信息科学与工程学院&国家超级计算长沙中心, 湖南 长沙 410082；

2. 国防科技大学计算机学院, 湖南 长沙 410073；

3. 中国人民解放军军事医学科学院, 北京 100850

1 引言

近年来，随着生物技术的发展，生物信息的数据量达到了一个更高的级别，生物医药领域的实验手段和研究方法均发生了巨大的变革，呈现出“大数据”的趋势，传统的单机计算已经不足以应对海量的数据和繁重的计算任务。对于大数据处理，常用的思路是并行计算，其包括多进程和多线程两种并行等级。生物效应分析流程主要包括比对和聚类。本文主要针对大量药物化合物制剂刺激下人体细胞反应的基因表达谱数据，完成细胞反应大数据的分析处理。主要分为以下3个步骤。

● 数据预处理：利用开源工具1KTools对整合网络细胞印记库（library of integrated network-based cellular signatures，LINCS）的原始基因谱数据进行预处理，得到实验核心程序能够使用的数据格式并写出文件。

● 基因探针富集分析（gene set enrichment analysis，GSEA）算法的核心实现：利用预处理后的数据完成富集积分矩阵的计算，采用MPI+OpenMP二级并行的策略负载均衡地划分数据，充分利用资源完成计算，并按进程写出结果文件。

● 并行聚类：以比对结果为输入，实现K-medoids[1]聚类算法及其优化，并对每次迭代过程同样利用MPI+OpenMP二级并行的策略进行并行化加速，最后将聚类结果写出到文件，每个表达谱归属于某一聚类。

2 相关工作

2.1 生物效应评估方法

随着生物技术的飞速发展，特别是以新一代测序技术为代表的高通量分析技术的发展，生命科学的年数据产出能力已经达到PB级，呈现出“大数据”的趋势，涉及海量的组学数据、文献数据、临床数据等。仅公开的数据库（如GEO[2]、ArrayExpress[3]、TCGA[4]等）就包含了大量病原微生物感染刺激下人体细胞反应的基因表达谱数据。2010年美国国立卫生研究院（NIH）启动了LINCS项目[5]，其目标是系统地检测15 000种化学分子对15种典型人体细胞刺激后的基因表达情况。目前该计划第一期已获得15种典型细胞中3 000余个基因沉默和5 000余种化学小分子刺激下的130余万个全基因组表达谱。

“生物效应评估”字面上理解就是评估这些生物制剂对人体细胞产生的效应，具体而言就是指评估这种生物制剂究竟会致使某种疾病还是治愈某种疾病。从而仅通过计算手段快速确定相关的检测标识物和治疗靶标，极大地缩短防治手段的研发过程，以快速有效地应对可能的生物威胁，给人类健康提供更多的保障。

对于转录组数据的比较指标，采用了GSEA[6-8]算法中提出的富集积分，它基于排序的Kolmogorov-Smirnov检验统计量计算方法，并且采用显著性分析、多重假设检验的方法对得到的富集积分进行统计分析，衡量结果的可靠性。

2.2 高性能计算技术在生物效应评估中的需求

目前GSEA在表达谱分析中得到广泛应用，随着 RNA-seq和低成本转录组L1000技术的流行，越来越多的大规模转录组数据出现，对于这样大规模的数据分析研究，往往需要快速的GSEA计算过程以支持数据挖掘和机器学习应用。于是，为了应对大数据场景下快速计算的需求，就有了利用超级计算对计算过程进行分布式并行加速的必要。

目前国内高性能计算技术也取得了丰硕的成果，其与世界先进水平高性能计算机之间的差距正在逐步缩小，6次蝉联超级计算机Top 500第一名[9]的“天河二号”代表着我国超级计算机的卓越成绩。

3 算法介绍

3.1 GSEA算法

GSEA算法主要用于分析两个不同表形样本集之间的表达差异，其基本思想是检验所定义基因集（gene set）S中的基因在整个微阵列实验测得的已排序的所有基因列表（gene list）L中是均匀分布的还是集中于顶端或底部的。其本身是非常丰富、全面的，包含大量的统计学分析手段，分为3个主要步骤：富集积分的计算、估计效应量（effect size，ES）显著性水平、调整多重假设检验。

其核心是使用Kolmogorov-Smirnov统计量进行富集积分计算，反映某个基因集在整个排序列表的顶部或底部集中出现的程度。ES的计算是在基因列表L中顺序步移的，从初始值ES(S)开始，当步移中遇到S中的基因时，增加ES(S)，否则，减小ES(S)。增加或减小的幅度依赖于基因与表型间的相关程度。ES就是ES(S)整个步移过程中与0的最大偏差的绝对值最大的值。

ES的计算过程[8]如图1所示。

富集积分的计算框架总结如下。

根据样本数据表达相关性，对含有N个基因的表达谱进行排序，得到有序的基因谱L={g1,g2,…,gn}，使得序列第j个位置的基因表达量就是第j个基因gj的表达量，即有式r(gj)=rj成立。

计算基因集（基因探针）S在序列L上的hit向量和miss向量，计算式如式（1）和式（2）所示。

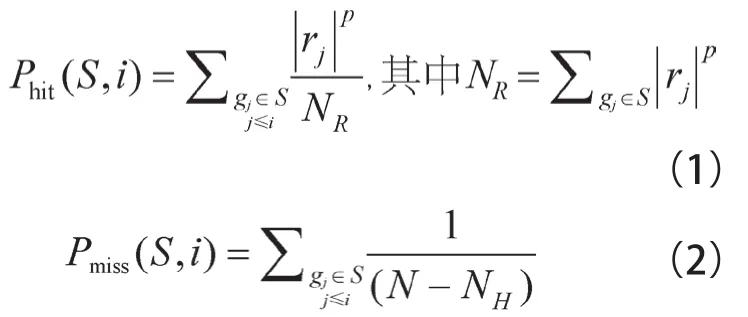
当随机选取基因集S时，ES(S)会相对较小，但是如果其聚集在L的尾部或者顶端，会有一个很大的ES(S)值。当p=0（指数）的时候，ES(S)将会减变为标准Kolmogorov-Smirnov统计分布（这是一个判别两个未知分布的总体是否有同一分布的非参数检验）。

在实际实现时，预排序工作和计算Phit、Pmiss按照式（1）和式（2）计算。而找最大偏离处的ES值，一般是先对Phit和Pmiss两个向量进行前缀求和，求和的过程中再对当前迭代次的前缀项作差，记录最大的差值项。当遍历完整个序列L时，就得到了最后的富集积分ES。

基于求解富集积分的算法描述过程可以清晰地分析算法各部分的时间复杂度，假设序列L长度为n，S的长度为m，算法的完成主要包含以下3个步骤的工作。

步骤1 对原始基因谱进行表达量排序：一般是达到O（nlogn）。

步骤2 计算Phit、Pmiss向量：每判断一个表达谱基因是否命中就要扫描整个探针S，故而时间复杂度为O（mn）。

步骤3 求解ES：算法描述中也提到需要对步骤2中两个向量进行遍历计算前缀和，故而时间复杂度为O（n）。

综上所述，GSEA是对表达谱进行分析的有效手段，但目前已有的实现工具（如R语言实现的GSEA-P-R.1.0[10]，Python实现的SAM-GS[11]以及Matlab实现的GSEA2[12]）都受限于脚本语言的低效性，难以达到需求的计算速度，同时它们对原本算法的实现极其直接，没有进行任何的性能优化，也没有使用任何的并行化加速手段，这就导致其对海量表达谱数据的分析难以满足实际的时间需求。因而急需更加有效的并行加速手段完成GSEA的快速分析[13]。

3.2 K-medoids聚类算法

经典的K-means[14]算法处理大数据集合时非常高效且伸缩性较好。但当聚类的样本中有“噪声”（离群点）时，会产生较大的误差，“噪声”对确定新一轮质心影响较大，造成所得质点和实际质点位置偏差过大。为了解决该问题，本文采用的K-medoids[1]聚类算法提出了新的质点选取方式，而不是像K-means算法一样简单地采用均值计算法。

在K-medoids算法中，每次迭代后的质点都是从聚类的样本点中选取的，而选取的标准就是当该样本点成为新的质点后能提高类簇的聚类质量，使类簇更紧凑[15]。该算法使用绝对误差标准来定义一个类簇的紧凑程度。而在实现中是直接选取当前类簇中与其他元素平均距离最近的点作为新的聚类中心。另一方面，之所以选择这个聚类算法也是因为它始终从已有的点中寻找新的中心，这就意味着计算过程中不会产生新的中心点，也就无需重新计算相似度，进而也就不需要返回比对算法部分重新计算富集积分。

然而，该算法具有同K-means算法一样的一些缺陷，比如：K-medoids也需要随机地产生初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。本文通过K-medoids++算法来优化这部分计算。

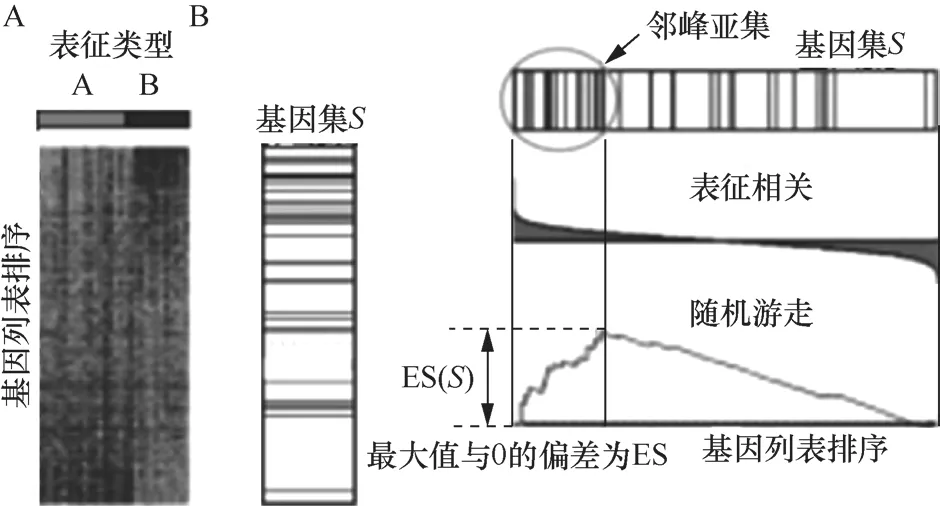
图1 ES的计算过程

K-medoids++算法选择初始质心的基本思想是：初始的聚类中心之间的相互距离要尽可能地远。其算法描述如下：

步骤1 从输入的数据点集合中随机选择一个点作为第一个聚类中心；

步骤2 对于数据集中的每一个点x，计算它与最近聚类中心（指已选择的聚类中心）的距离D(x)；

步骤3 选择一个新的数据点作为新的聚类中心，D(x)较大的点，被选取作为聚类中心的概率较大；

步骤4 重复步骤2和步骤3直到k个聚类中心被选出来；

步骤5 利用这k个初始聚类中心来运行标准K-medoids算法。

为了分析其复杂性，首先必须明确由于算法的执行存在随机性，不能形式化地判断它经过多少次迭代后收敛，因此对于算法复杂度的分析只针对单次迭代过程，假设有n个数据点和k个中心，复杂度分析如下。

● 生成初始聚类中心：对于每个数据点都要遍历已有的每一个聚类中心，从而找到离它最近的中心，然后从这几个最近中心中找到那个距离最远的点作为新的初始中心，如此重复k次。初略估计复杂度约为：O（k（kn+n））=O（k2n）（如果不是K-medoids++，直接随机生成这一步基本没有开销）。

● 划分数据到类簇：每个点遍历各聚类中心O（kn）。

● 寻找新的聚类中心：每个点要在各自的类簇中计算它到其他点的平均距离，然后再在各自的类簇中确定平均距离最小的点作为新的聚类中心，综合来看这一步的时间复杂度是O（n2）。

综上所述，开销最大的是寻找新中心的部分，至于生成初始中心的过程，因为始终只有一次，当迭代次数比较多的时候可以忽略不计。

4 基于MPI和OpenMP的并行优化

4.1 基因谱比对算法的优化

针对标准富集积分的计算在并行和循环过程中可能存在的优化部分，本文在成功移植GSEA算法后，有针对性地进行了优化，主要分为优化单独的计算例程和消除多次计算中出现的冗余计算两部分。

4.1.1 优化富集积分标准计算例程

由于实验过程会重复地计算富集积分，优化该步骤势必会获得较为理想的性能加速效果，所以不再根据GSEA算法按部就班地直接实现富集积分的计算，而是采用下面的优化策略。

（1）只考察命中位置

回顾富集积分的计算过程，通过在基因列表L中顺序步移，从初始值ES(S)开始，当步移中遇到S中的基因时，则增加ES(S)，否则，减小ES(S)。增加或减小的幅度依赖于基因与表型间的相关程度。ES就是ES(S)整个步移过程中与0的最大偏差的绝对值最大的值。通过观察分析不难发现，最大偏差位置只会出现在命中位置附近。若命中基因的前一个基因未被命中，则其前一个基因有可能为低峰；若其后一个基因未被命中，则其后一位置可能为目前的高峰。

（2）对命中基因排序

命中向量的命中位置对于计算富集积分至关重要，在计算开始前，对命中向量根据其命中位置排序可以直接得出命中位置的ES(S)值，即其未被命中的个数为其位置减1，进一步省去标准计算例程中的前缀求和部分。通过优化，可以把GSEA中富集积分前缀求和的复杂度由O（n）降低为O（lbm）+O（m）。而在实际情况中，基因谱的长度一般来说远大于上下调基因集的长度，也就是n远大于m。当大规模重复进行富集积分标准计算流程时，这样的优化将会带来十分可观的性能提升。

4.1.2 消除冗余计算

（1）预排序

因为任务是基因谱的两两比对，所以同一个基因谱在计算过程中肯定会被重复用到。而对同一个基因谱的排序工作也会因此反复地进行，这些都是没有必要的工作。于是在读入文件后就先对所有的基因谱进行预排序，之后处理的都将是排序后的转录组基因谱，从而排除冗余的排序过程。

（2）建立位置索引

富集积分的计算过程首先计算一个命中向量，即一个基因谱的上调或下调基因集在另一个排好序的基因谱中出现的位置，而这步操作需要循环遍历基因谱和基因集。如果基因集的长度是m，基因谱的长度是n，这样该步骤将是一个时间复杂度为O（mn）的操作。为了提高效率，系统先扫描一遍基因谱建立每个基因的位置索引数组，然后再扫描一遍基因集即可完成工作，从而将时间复杂度减小到O（m+n），并且用索引数组替代原来的排序基因谱也并不会造成额外的空间开销。

（3）构建三元组保存基因谱结构

与排序一样的问题，同一个基因谱会因为两两比对反复地建立索引，这还是冗余的操作。同样地，在完成预排序的同时就先为每个基因谱建立索引并用之替代原来的排序基因谱。但是只有索引数组并不能确定原来基因的上下调基因集，故而在读入数据后的预处理部分，用一个三元组保存基因谱的结构，它分别由上调基因集、下调基因集和索引数组三部分组成。

4.2 基因谱比对算法的并行优化

本实验的并行并不是对单次计算富集积分的算法过程进行的，而是通过有效的数据划分和负载均衡手段对大规模计算富集积分矩阵的过程进行的。其原因是：第一，单次富集积分的算法本身不适合并行，虽然有些前缀求和的操作也能通过消除循环依赖的办法强行并行，但是这会增加整体的工作量，得不偿失；第二，只计算一个富集积分即使在全基因长度2万多的基因谱上也不是个很大的工作量，对它并行粒度太小，反而会大量增加额外调度开销。

为了达到计算过程负载均衡的目标，实验首先对数据在进程间进行合理的划分。因为软件的输入是两个基因谱集的文件，所以数据的划分其实就是对这两个文件的划分，使每个进程拥有大致等量的待计算基因谱。

基于此，对于文件1，系统直接按进程数进行划分，使每个进程持有文件1的基因谱数相差不超过1，如果文件1的基因谱数刚好能够被启动的进程数整除，则它将被均匀地划分给每个进程，这是容易做到的。对于文件2，如果再将它按进程进行负载均衡的划分，将不能完成两文件中任意两个基因谱的比对工作。比如分给进程0的文件1的数据将不能与分给进程1的文件2的数据进行比对，如果强行比对，各进程在计算的过程中还要进行大规模的通信工作，这样做的开销是巨大的。于是，在一般内存足够的情况下，选择牺牲一定空间的策略，让每个进程持有文件2的全部基因谱数据，最大限度地保障了系统的计算性能。

相应地，在进程内部，采用多线程的策略对文件2的数据进行负载均衡的划分与计算。因为线程任务先天共享内存，这样，就可以充分发挥多核并行的优势，完成大规模并行计算工作。

整个数据划分方式如图2所示。

图2清楚地显示出两个文件的基因谱数据在各进程以及进程内部的线程中的划分方式，同时可以看到，最后每个进程会将结果写到各个子矩阵行。

对于具体的实现，文件1直接用封装好的I/O函数定位相应的部分数据进行读取。对于文件2，提供了3种通信方式。第一种方式是直接由每个进程读取文件2的全部数据，这样将不存在任何通信工作，但是也没有体现任何的并行工作。第二种方式是让一个进程读取文件2的全部数据，然后将之均匀地划分给每个进程，但这样不仅要像前一种方法一样等待一个进程读完一个完整文件2，还要再进行通信，显然数据划分的性能并不理想。第三种方式是，让每个进程一开始只并行地读取文件2的部分数据，然后通过全局通信操作让每个进程持有文件2的全部数据，这样读文件的时间将被大大地缩短。如果全局操作的实现足够高效，即使加上额外的通信，也将获得可观的性能提升。在实验中可以首先对比3种通信方式的运行效率，然后选择最佳方式继续实验数据的测试工作。

4.3 聚类算法的并行实现

图2 总体数据划分

聚类实验的并行化就是对K-medoids算法的并行化，没有太多的优化技巧，只在比对结果的基础上先由每个进程读入自己的那部分ES矩阵行，每一行代表一个基因谱相对于其他所有基因谱的距离向量，在后面的算法过程中，每个进程都只进行自己这几行基因谱的计算，其中会用集合通信的方式在各进程间全局维护一个类标记向量，这就是利用信息传递接口（MPI）完成的进程级并行。至于每个进程对持有的基因谱集进行划分以充分利用单节点处理器资源完成类簇规划和寻找新中心的操作，是OpenMP完成的线程级并行工作。每次聚类迭代并行化实现框架如图3所示。

如图3所示，在并行实现的过程中仍有许多细节需要注意，其具体实现如下所述。

步骤1 每个进程读取其下部分ES矩阵结果（由其序号，故而这部分进程数应该与之前计算ES矩阵并行写文件时一致）。

图3 每次聚类迭代并行化实现框架

步骤2 每个进程下生成一个长度为n1的类标记向量local_classflag，作为全局类标记向量的局部，所有进程的向量总长应为基因谱总数n。同时每个进程内应该保有自己每行基因谱的global_rank起始号，由基因谱总数与进程数就可计算判定。

步骤3 生成0～n的k个不重复的随机数，作为k个初始聚类中心。

步骤4 划分类：每个进程利用OpenMP并行加速，判断进程中每一行表达谱的归属类（根据其到k个聚类中心的距离，选取距离最小的聚类中心作为归属类），将local_classflag对应位置标记为该聚类中心编号。

步骤5 找新聚类中心：合并local_classflag为global_classflag到0号进程，然后广播给其他进程（当然如果是平均划分的可以直接Allgather）。每个进程将local_avedis对应的位置设置成其每一行基因谱到同一归属类其他基因谱的平均距离，然后将这些局部平均长度向量合并到0号进程的global_avedis向量，其长度为基因谱总数n。找到每类中平均长度最小的基因谱作为新的聚类中心。

步骤6 判断和之前相比，聚类中心是否发生变化，若无变化则停止，并输出相应结果；否则，重复执行步骤4。

值得注意的是，这里基因谱之间的距离是用富集积分的倒数来进行衡量的，ES值越大说明基因谱越相似，距离就越近，故而这样处理很容易理解。对于优化的K-Medoids++算法，只是在步骤3中进行更多的操作，按算法介绍的流程生成初始聚类中心。

5 实验结果分析

实验的原始表达谱数据来自LINCS项目，现已提供在GEO官网。

它有在各种实验条件下得到的多种规模的表达谱数据，一般是以.gct或者.gctx为后缀的HDF5文件格式。因为实验中直接采用1KTools开源工具进行原始数据解析，所以并不关注该文件本身的复杂结构，只需解析所需的表达谱数据即可。lKTools项目现在还在维护之中，提供了R、Java、Matlab和Python 4种语言的解析包，本文主要使用的是Matlab版本。

程序中主要解析了表达谱的3类数据。

● mat：基因谱集的表型矩阵。

● rid：每个基因的标识。

● cid：每个表达谱的标识。

5.1 基因谱两两比对，计算富集积分矩阵实验分析

实验中在“天河二号”上使用了包含2万基因谱的数据集进行实验，设置不同的并行程度，记录各部分的运行时间，以研究程序的性能和可拓展性。实验结果见表1。

由表1可知，数据载入部分的时间开销是比较小的，说明并行文件读入还是比较高效的。另外，对3种通信模式的性能进行分析，可以看到，全局通信优于无通信且优于点对点通信。分析3种模式实现策略不难发现这样的结果还是比较合理的。首先点对点通信效果最差，是由于它要先等0号进程读完整个文件后，再由0号进程将数据发给其他进程。因为在无通信的情况下，它只花费读文件的时间，所以这种点对点通信策略的性能会次于无通信策略，但是它能减少系统总体的通信开销。

全局通信每个进程只读取部分文件，然后通过Allgather操作将数据整合并发给全部进程，这样整体的I/O是比较小的，并且可以并行完成，只是多了大量的通信。显然它是有可能在性能上优于无通信策略的。而测试的结果也确实如此。

表1 基因谱比对实验各阶段运行记录表

写文件的操作以进程数为基准划分，可以看到，在相同进程数下，写文件的时间是大致相同的。而不同进程数下，测试结果也表现出比较好的可拓展性。

ES矩阵的计算部分也体现出较好的可拓展性。前期看来，基本是每增加一倍的并行度，运行时间就缩短一半，效率接近于1，理想上已经趋近于强可拓展的应用。整体来看，效果比较理想。当然，不能保证继续增加并行度，这样的效果还可以继续保持。所以扩大数据规模和并行程度，用5万的基因谱集进行对比分析，结果如图4所示。

从图4中可以看出，数据集规模越大，在扩大并行度时，并行效率保持得越高。这意味着在集群规模足够大的情况下，本文实验的程序可极好地适应大规模数据分析的需求。

5.2 基因谱聚类实验分析

（1）性能分析

使用2万规模和5万规模基因谱数据集比较单次迭代过程中两种聚类算法的执行效率，如图5所示。

因为算法的随机性，相同参数下多次运行程序执行的收敛步数是不一样的，所以不能用总的执行时间评估算法的性能，只能如图5一样根据单次迭代执行时间来分析，并将其转换成并行效率。

不难看出，在每次迭代的过程中算法都保持了比较良好的可拓展性，前期算法都会维持接近于1的高效率。同时在数据集规模相同的情况下，K-medoids和K-medoids++的实现效率也基本接近，它们只在寻找初始聚类中心时不同，并不会对后面每次的迭代过程产生太大影响。

（2）算法收敛性评估

有效的聚类算法必须能够快速地收敛，该部分实验在60核的条件下对不同聚类算法的收敛步数与执行时间进行评估，其结果如图6所示。可以发现聚类数越多，收敛越慢，执行时间也越长。另外，由于K-medoids++在生成初始聚类中心时尽可能地保证了样本空间距离足够远，所以它相对于K-medoids能够更快地收敛，效果也更佳。同时，也能够发现在相同聚类数目下，数据规模越大，收敛也可能越快。

另外值得注意的是，如果算法在非相邻的两次迭代中得到了相同的新聚类中心，将导致其不收敛的情况发生。为了避免出现这种情况，改进的实验中维护了一个聚类中心集列表，每次迭代中产生的未出现过的新聚类中心将被添加其中，如果新中心已经存在于列表中，则算法收敛。但该策略的缺点也是十分明显的：首先，迭代多次后，该列表会越来越长，消耗大量内存；同时，遍历列表判断算法是否收敛的开销也会越来越大。因此建议即使数据集足够大，也不要把聚类中心数设置得太多（比如超过500个），这样算法还是能够在开销过大之前有效地收敛的。

图4 不同规模数据集并行效率比较

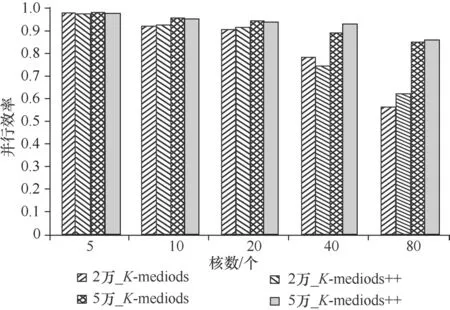
图5 单次迭代聚类算法并行效率比较

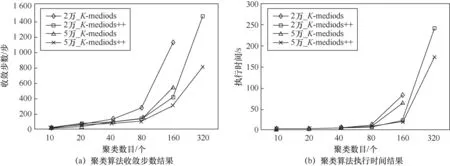
图6 不同聚类中心数目下收敛步数和执行时间

6 结束语

本文通过比对和聚类分析实现生物效应的快速评估，通过优化和并行加速，在极短的时间内完成细胞反应大数据的分析处理。同时，对比2万数据量和5万数据量的结果可以发现，在比对和聚类算法的实现中，扩大并行度时，数据量越大，并行效率越高且保持得越久，算法收敛越快，展现了实验的可拓展性和收敛性。总体来说，实验达到了预期目标。

[1]PARK H S, JUN C H. A simple and fast algorithm for K-medoids clustering[J].Expert Systems with Applications, 2009,36(2): 3336-3341.

[2]BARRETT T, TROUP D B, WILHITE S E,et al. NCBI GEO: archive for functional genomics data sets[J]. Nucleic Acids Research,2013, 41(Database Issue): 991-995.

[3]PARKINSON H, KAPUSHESKY M,SHOJATALAB M, et al. ArrayExpress-a public database of microarray experiments and gene expression profiles[J]. Nucleic Acids Research, 2007, 35(Database Issue): 747-750.

[4]KATARZYNA T, PATRYCJA C, MACIEJ W. The Cancer Genome Atlas (TCGA):an immeasurable source of knowledge[J].Contemporary Oncology, 2015, 19(1A):68-77.

[5]WON S J, WU H C, LIN K T, et al.Discovery of molecular mechanisms of lignan justicidin a using L1000 gene expression profiles and the Library of Integrated Network-based Cellular Signatures database[J]. Journal of Functional Foods, 2015, 16: 81-93.

[6]张威, 张扬, 曹文君, 等. GAGE和GSEA在基因集研究中的有效性比较[J]. 现代生物医学进展, 2013, 13(10): 1849-1852.ZHANG W, ZHANG Y, CAO W J, et al.Comparative study of GAGE and GSEA in Gene-set analysis[J]. Progress in Modern Biomedicine, 2013, 13(10): 1849-1852.

[7]冯春琼, 邹亚光, 周其赵, 等. GSEA在全基因组表达谱芯片数据分析中的应用[J]. 现代生物医学进展, 2009, 9(13): 2553-2557.FENG C Q, ZOU Y G, ZHOU Q Z, et al.The application of GSEA in data analysis of Genome microarray[J]. Progress in Modern Biomedicine, 2009, 9(13): 2553-2557.

[8]SUBRAMANIAN A, TAMAYO P,MOOTHA V K, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(43): 15545-15550.

[9]DONGARRA J. Visit to the National University for Defense Technology Changsha, China[R]. 2013.

[10]MOOTHA V K, LINDGREN C M,ERIKSSON K F, et al. PGC-1alpharesponsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes[J].Nature Genetics, 2003, 34(3): 267-273.

[11]DINU I, POTTER J D, MUELLER T, et al.Improving gene set analysis of microarray data by SAM-GS[J]. BMC Bioinformatics,2007, 8(1): 1-13.

[12]CARRO M S, WEI K L, ALVAREZ M J,et al. The transcriptional network for mesenchymal transformation of brain tumors[J]. Nature, 2010, 463(7279): 318-325.

[13]GAGGERO M, LEO S, MANCA S, et al.Parallelizing bioinformatics applications with MapReduce[J]. ResearchGate, 2008:1-6.

[14]MACQUEEN J B. Some Methods for classification and Analysis of Multivariate Observations[C]//The 5th Berkeley Symposium on Mathematical Statistics and Probability, June 21-July 18, 1965,California, USA. Berkeley: University of California Press, 1967: 281-297.

[15]刘小凤. 适用于RNA二级结构预测的改进K-medoids聚类算法研究[D]. 秦皇岛: 燕山大学, 2014.LIU X F. Research of suitableK-medoids clustering algorithm for RNA secondary structures prediction[D]. Qinhuangdao:Yanshan University, 2014.