应用PFC3D模拟道砟三轴试验

刘 力

(山东职业学院铁道工程与土木工程系， 山东 济南 250104)

0 引言

道砟作为粗砂砾或碎石用于铁路运输系统中，是轨道下部结构最重要的组成部分[1]。颗粒流理论是基于颗粒细观力学特征建立的一种简化的离散元法[2]，该方法将颗粒集料简化成具有一定形状、质量的颗粒的集合[3]，在研究道砟等散粒体的力学特性、相互作用等方面得到了广泛应用[2,4-8]。离散元程序PFC3D被认为是研究道砟微观力学性质的最适合的数值方法。[2,9]道砟的力学特性也可以通过微观颗粒尺度，如颗粒的平移、转动以及形态演化等解释。井国庆等[10]应用PFC3D模拟道砟三轴试验，研究道砟的宏观力学机理。张徐等[11]应用PFC3D建立道砟静态压碎的离散元模型，重点分析道砟的压碎强度。

本文基于William F. Anderson[12]的室内三轴试验结果，应用PFC3D模拟道砟的三轴试验，选取与室内试验一样的三轴仪尺寸、道砟密度及刚度等，比较二者的试验结果，验证参数一致时，PFC3D模拟室内试验结果的可行性，分析道砟的力学特性。

1 三轴压缩试验

1.1 William F. Anderson[12]的室内三轴试验

William F. Anderson对道砟进行室内三轴试验，轴室直径为0.236m，高为0.455米。道砟平均粒径50mm，最小压实密度和最大压实密度分别为1450kg/m3和1500 kg/m3，孔隙比e为0.806，道砟粒径40-50mm的百分含量为50%，粒径30-40mm的百分含量为40%，粒径10-30mm的百分含量为10%。分别取围压为40kPa, 90kPa和140kPa对道砟进行静力加载，得到试验结果。

1.2 颗粒流模型及参数的选定

本文选用接触粘结模型。颗粒法向刚度为1.1×108N/m。颗粒密度与室内试验道砟密度一致，取1450kg/m3。摩擦系数的选取参考井国庆等[10]的相关研究，设为0.5。参考文献[10]，墙体切向与法向刚度均设为 1×109N/m。设置侧墙刚度为颗粒刚度的1/10来模拟柔性边界[2]，孔隙率为0.446。为了真实模拟室内试验，数值模拟中采用与室内试验一致的轴室直径、轴室高度和道砟粒径级配。

1.3 生成模型及加载过程

利用 PFC3D通过“wall”命令生成高 0.455 m，直径为 0.236m的圆筒墙（cylindrical wall），为防止压缩过程中颗粒滑落，在矩形区域的直径方向延长0.5m，高度方向延长0.1m。利用内置的Fish语言编程，定义颗粒级配函数，从而生成不同粒径的颗粒，颗粒位置随机。

利用PFC3D中的伺服机制（Servo-Mechanism）模拟围压固定的应变控制式三轴试验，通过赋予上下墙体速度的方式对试样加载，加载过程中，使加载板的移动速度保持1mm/s。此伺服贯穿整个模拟加载阶段，通过Fish函数自动调整侧面墙体的位置，保证围压不变，加载过程中严格控制围压的误差不超过 0.5%。[2]William F. Anderson对道砟进行室内三轴试验，轴向应变达到8%时停止试验。本次数值模拟控制轴向应变达到8.2%时停止试验。

2 试验结果分析

分别取围压为40kPa，90kPa，140kPa进行数值模拟，记录每一个试样在围压下的应力、应变，并将模拟结果与室内试验结果对比，如图1、图2所示。

由图1可知，围压为40kPa和90kPa时，数值模拟结果与室内试验结果相关性比较好；围压为140kPa时，两种试验的结果比较接近。围压为40kPa，轴向应变为2%时，数值模拟试验与室内试验的偏应力均达到峰值，道砟试样产生破坏。围压为90kPa、140kPa时，轴向应变4%左右，试样基本破坏。不同围压下的偏应力-轴向应变曲线均呈应变软化型，可知，偏应力-应变曲线形态主要取决于围压高低，当围压较低时，曲线一般呈应变软化型。同一围压下，数值模拟的偏应力峰值大于室内试验得到的偏应力峰值，且软化现象更明显。

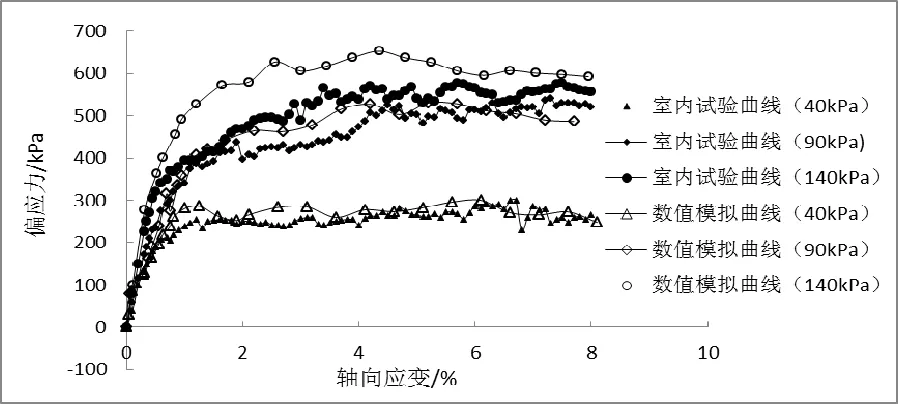
图1 数值模拟试验与室内试验偏应力-轴向应变曲线

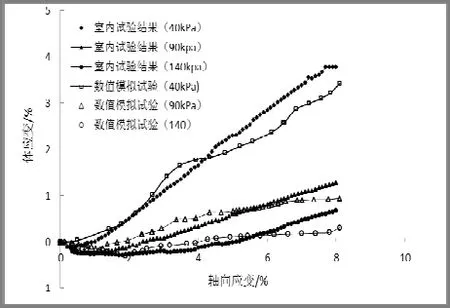
图2 数值模拟试验与室内试验体应变-轴向应变曲线

由图 2可知，不同围压下，数值模拟结果与室内试验结果相关性较好。试样先呈剪缩，后随着轴向应变的继续增加，试样呈剪胀。围压为40kPa，轴向应变大于2%后，体应变开始出现明显的增大，此时，试样基本破坏，与图1的分析结果一致。围压为90kPa、140kPa，轴向应变4%左右时，试样基本破坏，随着轴向应变的增大，剪胀不再明显。试样破坏之前，与室内试验相比，数值模拟试验的试样剪胀更明显。分析可知：低围压和剪胀使试样呈现软化现象。

3 结论

本文较为详细叙述了应用PFC3D模拟道砟三轴试验的模型及参数选定，将数值试验结果与已有的室内试验结果进行比较，分析道砟力学特性及内部力链分布，得到以下结论：

（1）轴室直径与道砟颗粒最大直径之比等于4.72。比较两次试验的应力应变结果，相关性较好，此时，尺寸效应的影响不是很明显。

（2）偏应力达到峰值时，试样基本破坏，围压越低，破坏时的轴向应变越小。

（3）低围压和剪胀都会造成试样的软化。

（4）同一围压时，数值模拟试验的试样比室内试验的试样软化现象要明显。

[1]Selig, E. T. & Waters, J. M. (1994). Track geotechnology and substructure management. Thomas Telford. London.

[2]刘力.基于离散元的碎石道砟力学特性研究[D].北京：北京交通大学，2015.

[3]JAEGER C, NAGLE S R, Behringer. The physics of the physics of granular materials[J]. Physics Today,1996,49(2):32-38.

[4]Lim W L, Mcdowell G R. Discrete element modelling of railway ballast [J].Granular Matter, 2005, 7(1): 19-29.

[5]Lu M, Mcdowell G R. Discrete element modelling of railway ballast under triaxial conditions [J].Geomechanics and Geoengineering, 2008, 3(4): 257-270.

[6]Stahl M, Konietzky H. Discrete element simulation of ballast and gravel under special consideration of grain-shape, grain-size and relative density [J]. Granular Matter, 2011, 13(4): 417-428.

[7]常在, 杨军, 程晓辉. 砂土强度和剪胀性的颗粒力学分析[J]. 工程力学,2010, 27(4): 95-104.

[8]马宗源, 徐清清, 党发宁. 碎石土地基动力夯实的颗粒流离散元数值分析[J]. 工程力学, 2013(增刊 1): 184-190.

[9]Wee Loon Lim, BEng (Hons). Mechanics of Railway Ballast Behaviour[D]The University of Nottingham,2004.

[10]井国庆,王子杰,施晓毅.多围压下三轴压缩试验与不可破裂颗粒离散元法分析[J]. 工程力学, 2015, 32(10): 82-88.

[11]张徐,赵春发,翟婉明. 铁路碎石道砟静态压碎行为数值模拟[J].西南交通大学学报,2015,50(1):137-143.

[12]WILLIAM F. ANDERSON，PETER FAIR. Behavior of Railroad Ballast under Monotonic and Cyclic Loading[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2008，134(3)：316-327