建筑物沉降监测技术与回归分析方法 在数据处理用的应用

王 钊 栗衍香

（1滨州市规划设计研究院， 山东 滨州 256600；2滨州市规划局， 山东 滨州 256600）

高层建筑物作为提升容积率、提高土地利用效率的重要方式，在现代城市规划建筑中不断涌现，然而高层建筑在施工建设和竣工使用过程中，必须对建筑物布设一定的监测点，周期性的采集点位的高程信息，通过对信息的统计分析，预防不均匀沉降等可能引起建筑物主体结构破坏的不良情况，为施工单位及时提供详实信息。

1 回归分析理论

回归分析，基于观测数据建立变量之间恰当的依赖关系，利用数理统计原理，对大量统计数据进行数学分析，确定因变量和自变量（沉降量与影响因子）间的关系，建立相关的数学模型。通常采用线性回归分析方法，寻求一个因变量相对于一个自变量间的因果关系，称为一元线性回归分析。

2 沉降监测点的实施程序与步骤

2.1 沉降监测点的布设与观测路线确定

沉降监测涉及的点位分为沉降监测基准点、工作基点和监测点，小范围内工作基点可兼做基准点使用，点位至少3个，环形闭合布设在远离沉降区的稳固处，并定期进行闭合水准联测；监测点应按照预先设定的高程控制网，预埋或后植在监测对象的主要拐点、沉降缝两侧和轴线交汇点等位置，周期性观测时均应基本按照同一路线进行水准测量。

2.2 沉降监测实施步骤

基准点测量与稳定性监测

沉降监测实施工期内，需要对基准点定期进行闭合环路水准测量，按JGJ8-2007《建筑变形测量规范》所规定的二级观测方案的精度要求，测量采用美国产 Trimble Dini03自动安平精密电子水准仪配以LD-2型条形码铟钢水准尺，经多次高程基准网复测成果表明，该基准点基准网稳定可靠。

基准点测量与稳定性监测

依照编写的技术设计方案及高层建筑物的设计特征，本工程共在1-4#楼体各布设沉降观测点 6个，分别置于建筑物四角及构建物中间部位，布点高度均为标准F1层±0之上0.3米处。

测量频率为：主体施工期间自第2层起，每2层观测1次；主体结构施工完成后装饰施工期，预计装修期半年左右，按沉降速率随时间的递减规律，分别在施工完成后的第1月、第3月、第5月各观测；竣工交付使用后每半年观测一次，直至楼体稳定终止，即最后几期所测各点的沉降速率均应小于说明基础沉降已趋于稳定。因故停工和复工前加测一次，停工期间每2月观测1次；根据观测资料情况，当沉降速率大于2mm/d时，采取措施，增加观测次数，并及时报甲方、监理单位。

3 沉降数据回归分析与模型检验

3.1 沉降数据建模分析

本文选取2#楼 N5点各监测时刻相对于前期高程值的单期沉降量（非累积沉降量），作为样本原始序列，分别用一元线性回归和多项式回归两种模型进行数学建模分析，原始数据和两种模型的预测结果如表1所示：

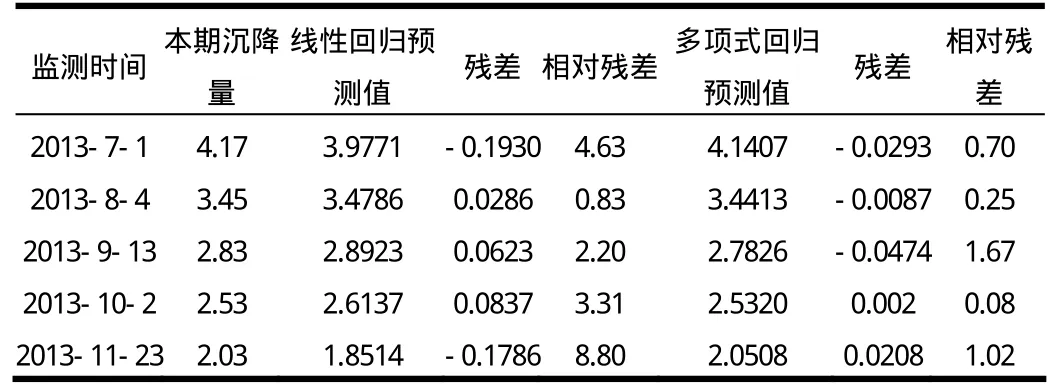
表1 回归分析模型预测对照表

利用 MATLAB软件进行数学建模运算，求得线性回归模型参数：一元线性回归方程为:利用该方程进行数值运算，可求得各期数据的估值；采用多项式回归模型求得参数：得到多项式回归方程为，利用该方程进行数值运算，可求得各期数据的估值。

3.2 回归模型检验

表2 回归分析模型评价表

通过表2模型精度评价和图1双回归模型的拟合效果对比可发现，两种回归模型均能在建模数据区间内，完好的反应数据的变化情况。但从偏差平方和（SSE）、均方根拟合标准差（RMSE）方面看，多项式回归效果明显优于一元线性回归分析，同时对于后期数据的拟合契合度更好，比一元线性回归更符合建筑物的变形规律。

4 结语

本文对建筑物沉降监测的工作流程进行了详细阐述，并在大量统计数据的基础上，分别采用一元线性回归和多项式回归进行建模分析，为建筑物沉降监测数据处理提供了一定的参考。由于实际工作中，建筑物沉降影响因素较多，沉降变化多呈现非线性的情况，此时可通过引入指数函数、幂函数等方式进行变量代换，将其先化为线性回归模型，再进行建模分析；同时在少样本、贫数据的情况下，也可引入灰色系统模型和神经网络相关理论，对沉降数据进行建模分析，并通过及时更替建模数据，从而获得最佳预测效果。