能量近似法在深水长桩自由站立分析中的应用

李 娟，尹晓明，王江宏，张孝卫，于志强

(海洋石油工程股份有限公司 天津300451)

0 引 言

桩基海洋平台的桩通常为打入式钢桩，采用蒸气、柴油或液压为动力的冲击锤将桩打入海底。桩无侧向支撑段长度为自由站立长度，此桩段所处状态为自由站立状态。在桩的安装过程中需对桩的自由站立强度进行校核，即校核安置桩锤至桩打入设计入泥深度期间由锤和桩的重力以及环境荷载(风波流)等引起的桩身应力是否满足桩身材料的强度要求。最常见的影响因素包括静弯矩、轴向荷载、桩锤初始放置时产生的侧向荷载和环境荷载等。

桩的破坏形式主要有强度破坏、整体失稳、局部失稳和疲劳破坏。对于直径大、壁厚薄和超长的桩，通常长细比较大，破坏形式多为整体失稳。欧拉公式作为经典理论公式，经常被用于计算轴心受压杆件的整体失稳许用应力，其采用的模型为“理想压杆模型”，即假定压杆轴线是理想直线，压力作用线与轴线重合，材料是均匀的，且两端受集中压力荷载。

美国石油协会(API)出版的《海上固定平台规划、设计和建造的推荐作法——工作应力设计法》[1]，中规定，当长细比超过一定值时，需要考虑结构的整体失稳并利用欧拉应力公式计算容许轴向压缩应力Fa。对于深水桩而言，不仅具有端部压载以及重量沿桩长分布的特性，而且由于桩长通常在 100,m以上，不同工况控制易导致壁厚较大，结构较重。侯涛等[2]指出，对于深水长桩，在计算容许轴向压缩应力时，应考虑重量对许用应力的影响。铁木辛柯应用弹性稳定理论[3]，考虑桩身重量沿桩长均匀分布，并给出了计算公式。这相当于整个自由站立桩段均采用单一壁厚计算，而实际桩身是由多种壁厚组成的。在应用中，保守考虑，一般会取自由站立桩段的最薄壁厚来计算桩的容许轴向压缩应力，计算结果偏小；当自由站立工况起控制作用时，会造成计算壁厚比实际所需要大，增加了桩身重量；同时桩的安装对其长度和重量比较敏感，重量越重，长度越长，对安装机具的要求越高。

本文以铁木辛柯弹性稳定理论为基础，按实际壁厚考虑沿桩长分布的重量，结合 API RP 2A-WSD[1]及 AISC[4]规范公式，运用能量近似法来计算桩是否满足稳定性要求，对现有自由站立的分析方法进行优化和改进。

1 能量近似法计算轴向许用荷载理论值

目前常用钢管桩外径相同，仅壁厚变化，许用荷载计算模型简单示意如图1。

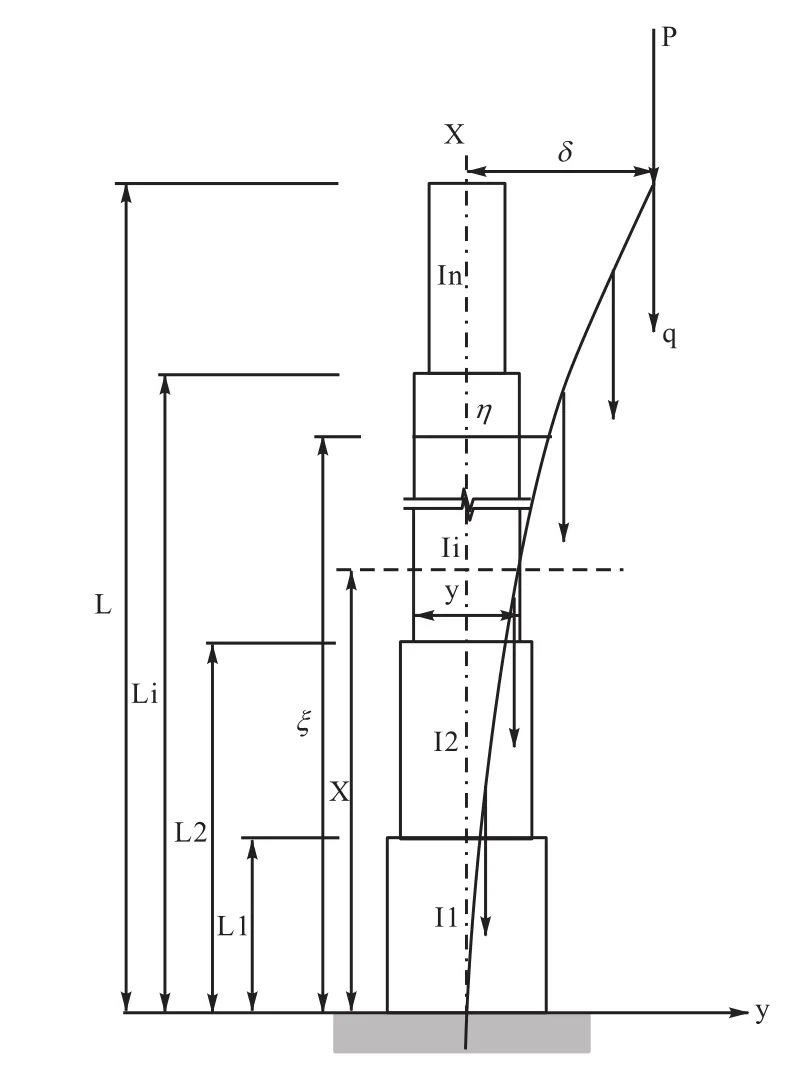
图1 轴向许用荷载计算模型Fig.1 Calculation model for axial allowable load

假定挠度曲线为：

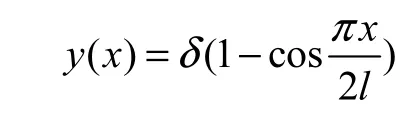
计算截面处弯矩：

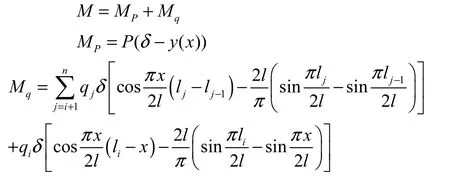
弯曲应变能：

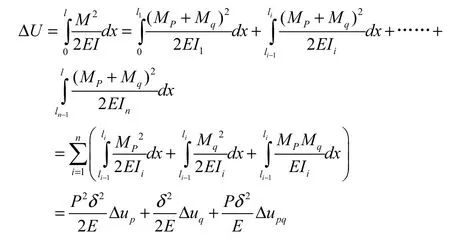
压力做功：

令 ΔU =ΔT ，有：

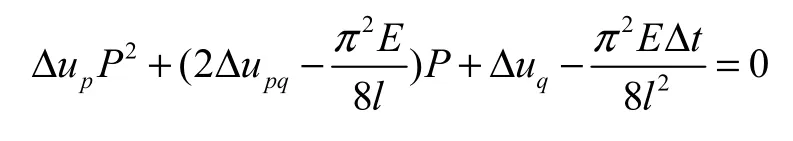
桩顶轴向许用荷载理论值：

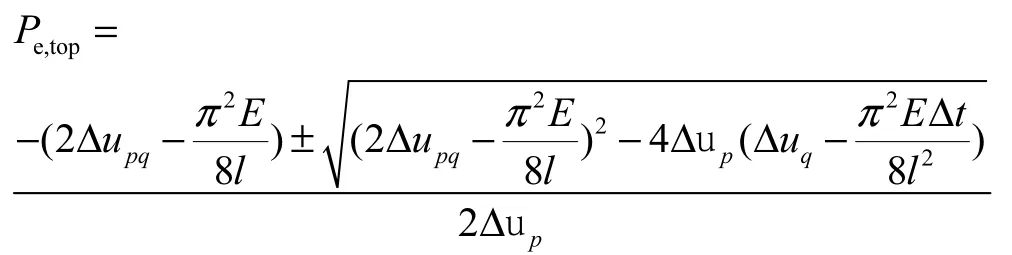
桩底轴向许用荷载理论值：

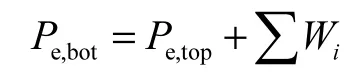
其中：iW∑为计算截面以上桩重，单位kN。

2 轴向许用荷载

API RP 2A-WSD[1]轴向许用应力的计算公式是根据欧拉公式和 AISC[4]规范提出的，本文采用能量近似法计算桩顶许用荷载，根据AISC规范：

当Fe≥0.44F时：Fcr=0.658（Fy/Fe）×Fy

当Fe＜0.44Fy时：Fcr= 0.877×Fe

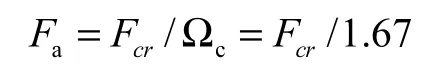
其中：Fa为允许轴向应力，单位 MPa；Fe为允许轴向应力理论值，单位 MPa；Fcr为允许轴向应力临界值，单位MPa；Fy为钢材屈服应力，单位MPa。

计算截面处轴向许用荷载：

当Fe≥0.44Fy时，Pall,TM=0.658（Fy/Fe）×Fy×A /1.67

当Fe＜0.44Fy时，

其中：A为桩横截面积(取与最大应力对应处横截面积)，单位 m2。

3 弯曲许用应力

纯弯时弯曲许用应力 Fbend，根据 API RP 2AWSD[1]公式3.2.3-1(a～c)计算得出。

对于压弯构件，弯曲许用应力需要考虑轴向应力的影响，弯曲许用应力Fall计算公式如下：

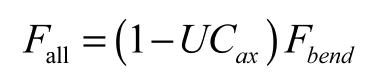
其中：UCax为轴向力产生UC值。

4 应力校核方法

桩自由站立时承受竖向压力及弯曲应力，为压弯构件，根据 API RP 2A-WSD公式 3.3.1-(1-2)，考虑桩身荷载的影响，校核如下：

屈曲校核：

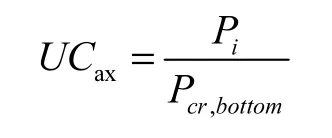
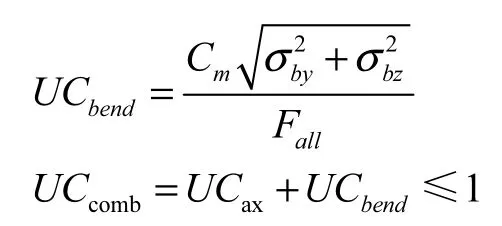
屈服校核：

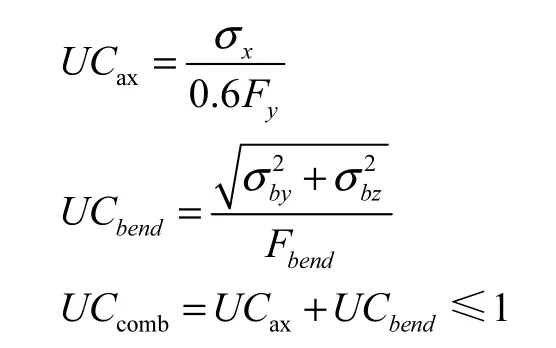
其中：σx为轴向压应力，单位MPa；Pi为计算截面承受轴向荷载，单位 kN；Cm为弯矩折减系数，取 1.0；σby、σbz为弯曲应力，单位MPa；Fbend为纯弯时弯曲许用应力，单位 MPa；U Cax为轴向压力产生 UC值；UCbend为弯曲应力产生 UC值；U Ccomb为自由站立组合应力产生UC值。

其他符号同前文。

5 自由站立分析计算工程实例

考虑一座导管架固定式平台所在水域的海图水深为-91.1,m，设计桩长127,m，桩径2.438,m，最终贯入深度为 105,m，进行桩自由站立分析的基础数据为：

①安装时，海上的环境条件：

波浪：Hmax＝2.6,m；Tmax＝6.35,s。

流速：海底为 0.3,m/s；中层为 0.3,m/s；表面为0.6,m/s。

②压桩所用锤为 MENCK MHU800S，锤特性见表 1。

表1 锤特性表Tab.1 Hammer parameters

③计算钢桩自由站立长度及倾角，自由站立长度105.9,m，桩倾斜角度 0.7 °。

④钢桩分段，详见表2。

⑤计算模型及计算方法详见文献[2]。

⑥计算分析程序。

桩锤系统建模和桩应力计算采用美国BENTLEY公司的SACS程序进行。许用应力的计算以及应力校核采用Excel编制程序计算。

⑦计算结果详见表3。

选取某工况进行计算，结果详见表3、4。

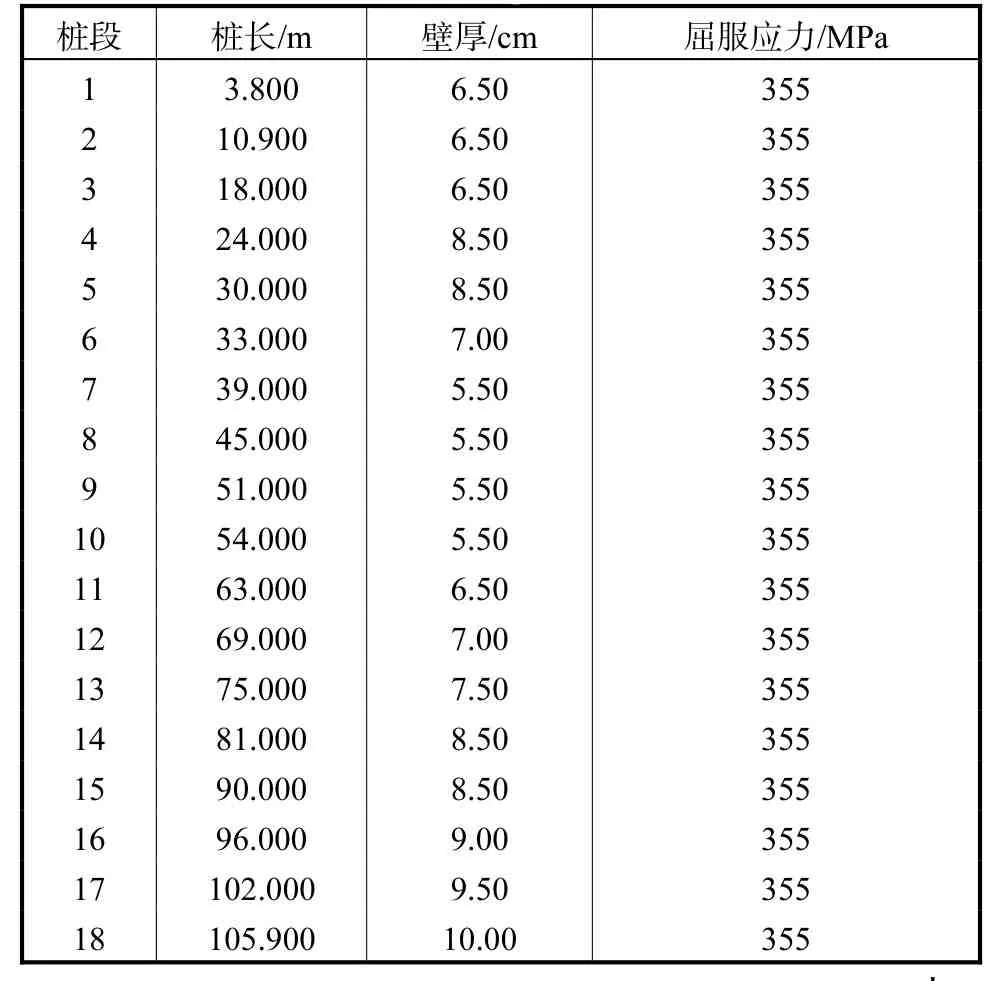
表2 钢桩分段Tab.2 Pile parameters

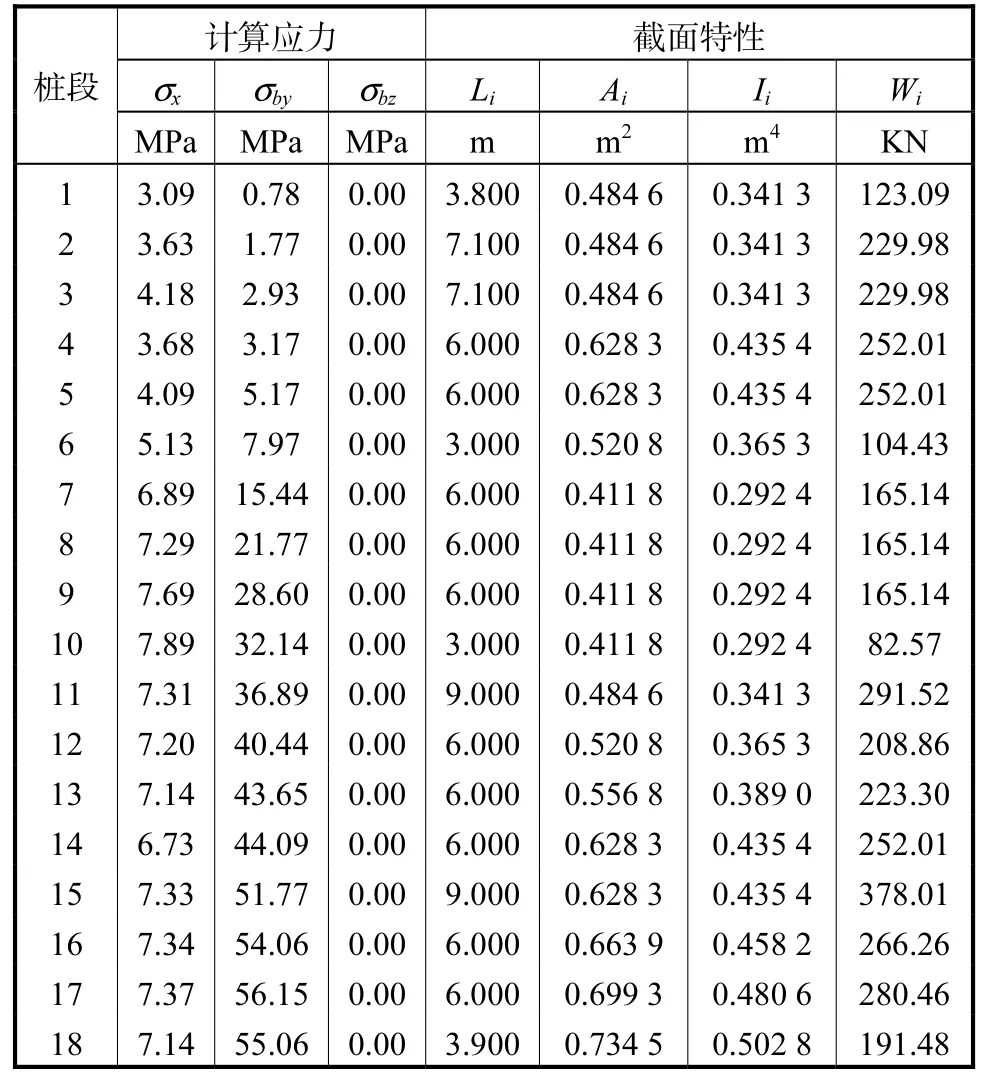
表3 计算结果Tab.3 Calculation results

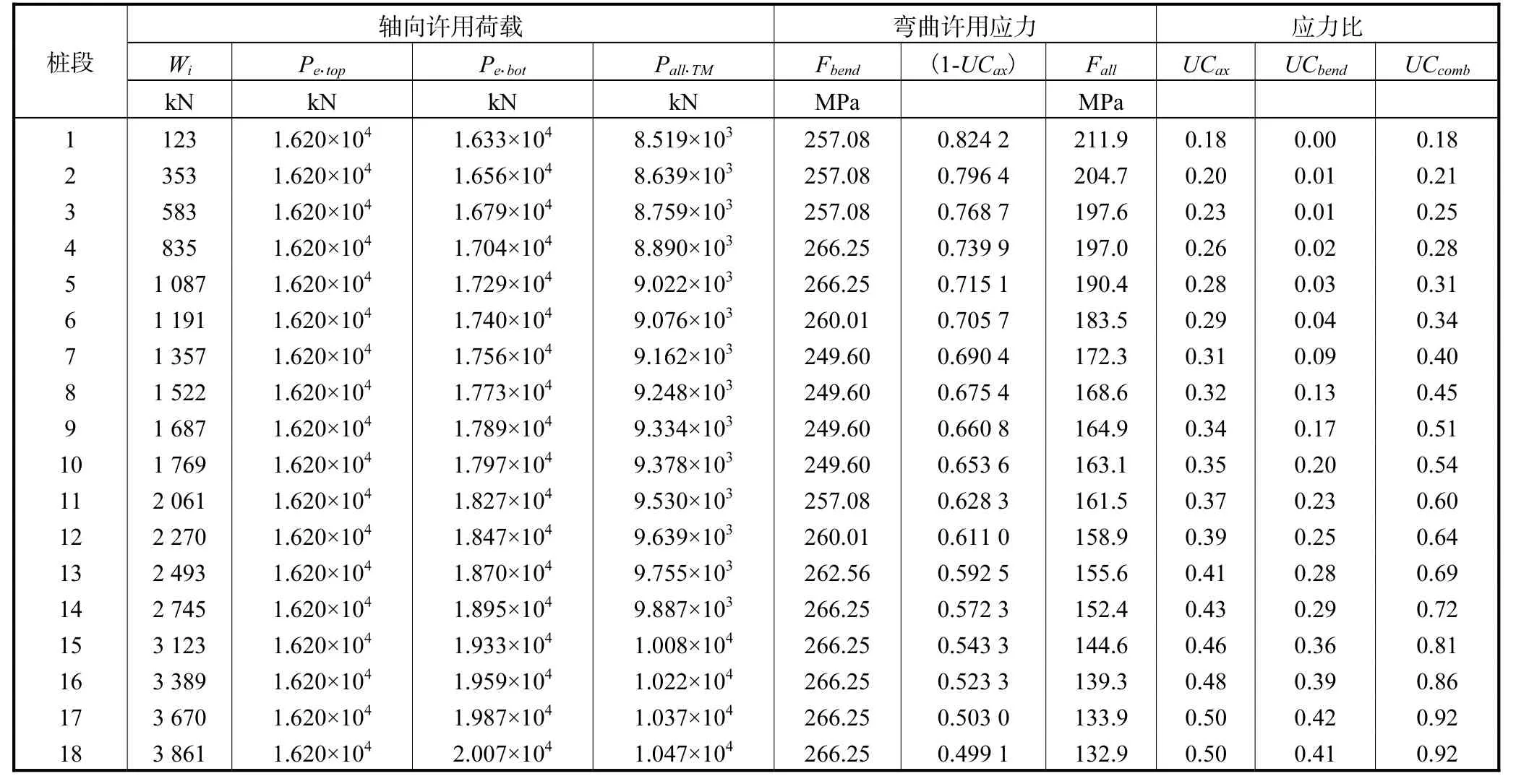
表4 计算结果Tab.4 Calculation results

⑧计算结果对比。取相同基础数据和计算工况，将本文计算方法所得计算结果与文献[2]计算方法所得结果相比较，详细结果见表 5。从计算结果可以看出，利用文献[2]计算方法的计算结果已经不满足要求，需要增加壁厚或加大桩径；而按照本文考虑实际壁厚沿桩长分布的能量近似法计算，现有桩段设计能够满足自由站立强度校核要求，优化效果明显，节省了工程费用。

6 结 论

本文依据铁木辛柯弹性稳定理论，采用能量近似法，在进行深水长桩自由站立轴向许用荷载计算时，考虑钢桩壁厚的实际分布，改进了现有的自由站立计算方法。工程实例表明：按照改进后的计算方法计算轴向许用荷载，可以减小钢桩壁厚，桩重也相应减小，节省了工程费用；自由站立桩段壁厚变化越大，优化效果越明显。■

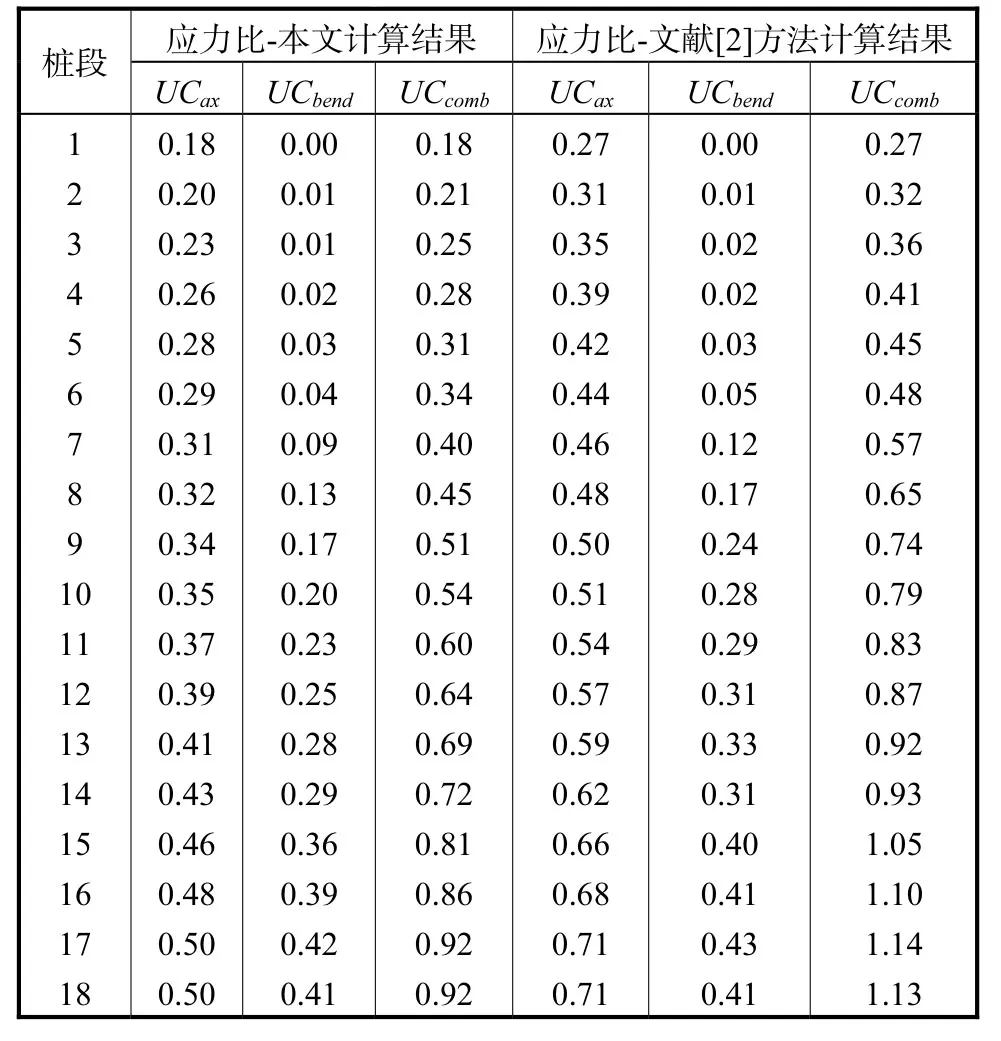
表5 计算结果对比Tab.5 Comparison of calculation results

［1］American Petroleum Institute.Recommended Practice for Planning，Designing and Constructing Fixed Offshore Platforms-Working Stress Design[S].API RP 2AWSD，21st Edition，2007.

［2］侯涛，张孝卫，刘洪涛，等.铁木辛柯弹性稳定理论在深水桩自由站立分析中的应用[J].中国海洋平台，2010，25(2)：34-38.

［3］铁木辛柯 S P，盖莱 J M.弹性稳性理论第二版[C].北京：科学出版社，1965.

［4］American Institute of Steel Construction INC.Specification for Structural Steel Buildings[S].13th Edition，2005.