不确定陀螺仪混沌系统的H∞滑模控制
2018-06-01张秀兰
李 媛,张秀兰
(1.山西传媒学院 传媒工程系,山西 晋中 030619;2.淮南师范学院 电子工程学院,安徽 淮南 232038)
过去的几十年中,由于在太空航空、航海航行以及光电科学中有很多应用,陀螺仪系统的控制问题引起了很多学者的关注[1-2]. 同时, 陀螺仪系统也展现出了丰富的动态性质,如极限环和混沌等.这些性质的发现对陀螺仪的实际应用也起到很好的促进作用.带有线性或者非线性阻尼的不同类型的陀螺仪系统的控制问题现在已经成为一个热门的研究方向.相关的研究成果主要可以分为如下三类:陀螺仪动力学及分线性分析[3-4], 混沌及其控制[2]以及同步[1, 5, 6].众所周知,H∞控制具有很好的控制效果和应用价值.目前,很少有文献研究陀螺仪系统的H∞控制问题.
滑模控制在处理不确定非线性系统的控制问题中有着广泛的应用.这种控制方法具有很好的鲁棒性以及控制效率[7-8].这种控制方法最重要的是实际合适的滑模面.滑模面的设计对最后的控制效果起到关键作用.滑模控制应用范围广泛,在陀螺仪系统的控制中也有一些具体应用[1,4,5].同时,H∞控制具有一些较好的控制特点.这些特点与滑模控制相结合,对控制系统的鲁棒性及控制效果的提升有一定的帮助[9-10].这也是本文研究的出发点.本文主要考虑对含有未知外界扰动的陀螺仪混沌系统设计滑模控制与H∞控制相结合的综合控制器.该控制器可以结合滑模控制和H∞控制的优点,提升整体的控制效果和系统的鲁棒性.
1 问题的描述与预备知识
本文考虑的对称陀螺仪的几何图形如图1所示.在线性阻尼的影响下,角度θ的动态方程可以描述为[2]:
(1)

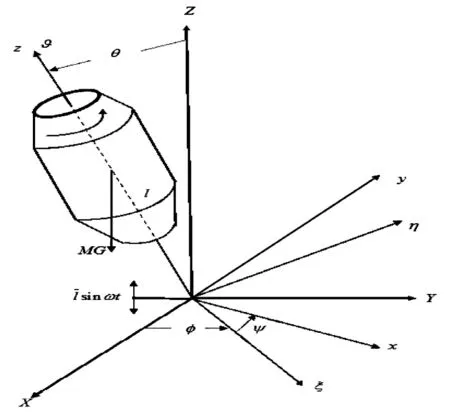
图1 对称陀螺仪工作示意图

(2)
其中d(t)为未知的外界扰动,u(t)为控制输入.
当系统参数选为f=35,α=10,β=1,c1=0.5,c3=0.05,ω=2时,系统(1)或其等价形式(2)具有混沌吸引子.设系统初值为x1(0)=1.6,x2(0)=0.其混沌示意图见图2.
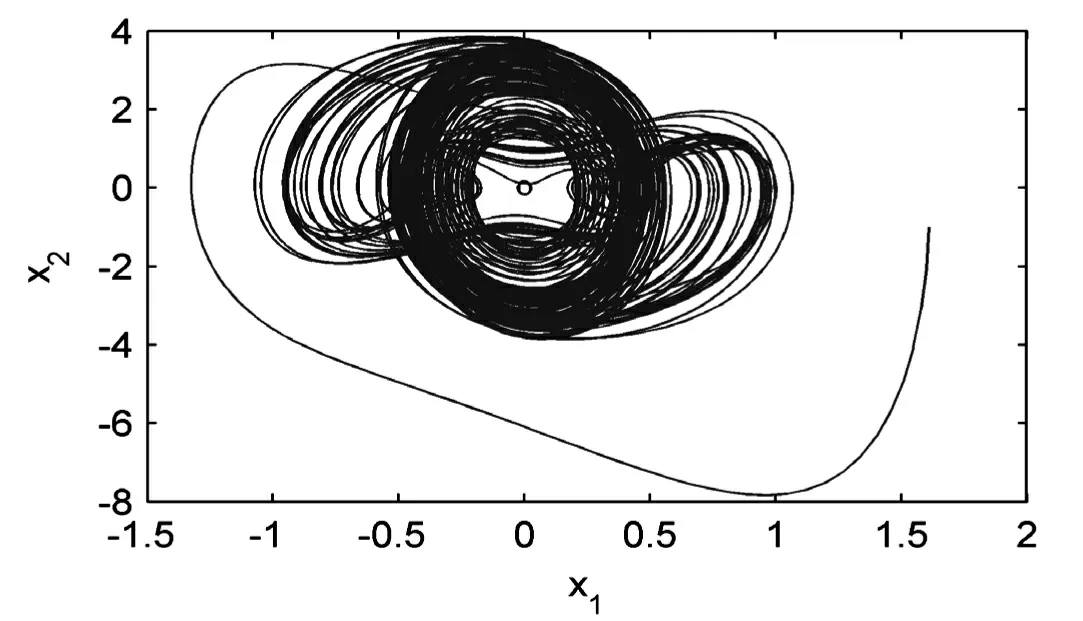
图2 陀螺仪系统混沌吸引子


(3)
本文假设系统输出满足如下的形式:
y(t)=Cx(t)+Dd(t)
(4)
其中C和D为适当维数的矩阵.
本文的主要目的是设计适当的滑模H∞控制器, 使得陀螺仪混沌系统(3)的状态向量满足如下条件:
(i) 在0初值的条件下,在滑模面上,闭环系统为渐近稳定的.存在大于零的常数r满足如下的H∞控制条件:
‖y(t)‖≤r‖d(t)‖
(5)
(ii) 设计合适的控制器,使系统状态向量在有限时间内到达滑模面,并在此时间以后停留在滑模面上.
为了完成控制目标和便于控制器的设计,我们给出如下假设:
假设1H∞性质参数r满足
DTD≤r2I.
(6)
假设2[10]系统未知的外界扰动d(t)满足d(t)∈L2[0+∞),即存在大于零0的常数Md使得
(7)
注需要指出的是假设1和2是合理的.对于假设1,本文要求未知矩阵D满足条件DTD≤r2I.事实上,很多未知的外界不确定项都满足此条件.常用的函数如sin(x(t)),cos(x(t))等都满足此条件.对于陀螺仪的系统模型是在理想情况下得到,对其实际工作状态我们增加考虑系统不确定项,这也是为了说明本文控制方法有较好的鲁棒性.对于假设2,我们假设外界扰动的能力是逐步衰减的,这是符合实际情况的.这个条件也是H∞控制实施的必要条件.
2 控制器的设计及稳定性分析
可以构造如下的滑模面:
(8)
其中G∈R1×2为常数矩阵且GB非奇异;K∈R1×2为满足一定条件的待选矩阵.于是可得系统等效控制器为
ueq=Kx-(GB)-1G[f(x)+d(t)]
(9)
等效控制器(9)可以使系统状态的动态方程满足

(10)
其中F=[I-B(GB)-1G].
于是可以给出本文的主要结果.
定理1 在满足假设1和2的条件下, 如果外界扰动d(t)=0, 对于给定的r,μ>0,如果存在正定矩阵P和实矩阵K满足
(11)
其中
∧=PA+ATP+PBK+KTBTP
(12)
则滑模面动态方程(10)为渐近稳定的.
证明由于d(t)=0, (10)式可以改写为

(13)
定义Lyapunov函数为
V1=xTPx.
(14)
于是

(15)
注意到如果选取μ足够大,可以使
μ2xTx≥fT(x)f(x).
(16)
进一步,有
(17)
其中α=[xT,fT(x)]T.
定理2 在满足假设1和2的条件下, 对给定的r,μ>0, 如果存在一正定矩阵P和一实矩阵K满足
(18)
则可以保证控制系统的H∞性能.
证明设Lyapunov函数为(14).在考虑外界扰动的情况下有

(19)
定义β(t)=[xT,fT(x),dT(t)]T, (19) 可以改写为

(20)
其中
再根据(18)可知

(21)
对(21)式两边取积分可得
(22)
于是可以保证系统的H∞性能.证毕.
注根据Schur补定理, (11) 和 (18)可以写为
(23)
根据上面的讨论,我们可以构造如下的控制器:
(24)
其中
η(x)=μ‖GF‖‖x‖+‖GF‖‖d(t)‖+δ
(25)
这里δ>0为设计参数.
定理3 在满足假设1和2的条件下, 如果滑模面设计为(8),K为LMI(23)的解, 控制器设计为(24) 和(25), 于是可以保证滑模面s(t)=0的可达性.
证明定义Lyapunov函数为
(26)
根据(8), (10), (24) 和(25)有
(27)
于是有

(28)
根据(28) 可知s(t)=0为可达的.证毕.
3 仿真研究
设系统参数为r=0.1,μ=0.5,δ=0.2.矩阵G为G=[1,1,2]T.于是根据(23), 可得K=
[-0.5474,0.1673,2.1456]T.外界扰动为

(29)
仿真结果见图3-5.从仿真结果看,被控对象x1和x2两个状态向量趋向原点,控制效果较好,得到了系统的H∞性能.

图3 控制输入

图4 状态向量x1控制效果

图5 状态向量x2控制效果
[1]Pechev A N. Feedback-based steering law for control moment gyros[J].Journal of Guidance Control & Dynamics,2015,30(3):848-855.
[2]Zarei M, Vali A, Behnamgol V. Sliding mode control with self-tuning law for synchonization of two uncertain chaotic gyros[C].International Conference on Control, Instrumentation, and Automation. Qazvin Iran:IEEE,2016.
[3]Kim Y W,Yoo H H. Design of a vibrating MEMS gyroscope considering design variable uncertainties[J].Journal of Mechanical Science and Technology, 2010, 24(11): 2175-2180.
[4]Tsai N, Wu B. Nonlinear dynamics and control for single-axis gyroscope systems[J].Nonlinear Dynamics,2008(51): 355-364.
[5]Zheng S, Li H, Han B, Yang J. Power consumption reduction for magnetic bearing systems during torque output of control moment gyros[J].IEEE Transactions on Power Electronics,2017,32(7): 5752-5759.
[6]Yau H T. Chaos synchronization of two uncertain chaotic nonlinear gyros using fuzzy sliding mode control[J].Mechanical Systems and Signal Processing,2008(22): 408-418.
[7]Dong Q, Zong Q, Tian B, Wang F. Adaptive‐gain multivariable super‐twisting sliding mode control for reentry RLV with torque perturbation[J].International Journal of Robust & Nonlinear Control, 2017, 27(4), in press.
[8]Zhang B, Ma L, Han Q. Sliding modeH∞control for offshore steel jacket platforms subject to nonlinear self-excited wave force and external disturbance[J].Nonlinear Analysis: Real World Applications,2013,14(1): 163-178.
[9]Luo Y, Wang Z, Liang J, Alsaadi F E.H∞Control for 2-D fuzzy systems with interval time-varying eelays and missing measurements [J].IEEE Transactions on Cybernetics,2016,47(2): 365-377.
[10]Cheng J, Park J H, Wang H. Event-triggered H∞control for T-S fuzzy nonlinear systems and its application to truck-trailer system [J].ISA Transactions, 2016(65): 62-71.
