状态耦合大规模系统的分布式预测控制

潘红光，米文毓，高海南，江能前

(1.西安科技大学 电气与控制工程学院，陕西 西安 710054；2.西安卫星测控中心，陕西 渭南 714000；3.西安交通大学 经济金融学院，陕西 西安 710049)

0 引 言

预测控制可被广泛应用于处理物理约束，并能提高控制性能；其在每个时刻求解优化问题获得一系列最优控制输入，但是仅实施第一个控制输入。关于预测控制的综述具体可参见文献[1-3]。针对大规模系统，采用集中式预测控制的计算量很大，甚至大到不能应用于实际。处理该问题的一个有效方案是将大规模系统分成若干个子系统，并针对每一个子系统采用分布式预测控制策略[4]。

一般来说，前述的子系统可分为动态解耦(如文献[5-6]中的多智能体系统)和动态耦合(如文献[7]中的电力系统及文献[8-9]中的工业过程系统)2类。对于每个子系统而言，称在代价函数、物理约束以及系统动态等方面与之相关的子系统为其邻居。特别地，在系统动态方面耦合的邻居子系统被称为动态(上游/下游)邻居。

在分布式预测控制中，每个子系统不能提前预知其邻居的当前实际预测轨迹，故需采用假设预测轨迹[10-11]。假设预测轨迹与实际预测轨迹之间存在差别，这些差别被称为不确定性偏差。对于动态耦合情形，每个子系统的状态演变直接依赖于其邻居子系统。因此，不确定偏差可能会导致严重的问题，如递归可行性和稳定性不能保证、违反物理约束等。

针对动态耦合子系统，已有文献给出了多种该处理方案：针对无约束子系统的方案可参见文献[12-13]；针对状态约束子系统的方案可参见文献[14]；针对输入约束子系统的方案可参见文献[7，15]。在文献[16]中，针对带有状态和输入约束的动态耦合系统，作者基于文献[17]的tube-based鲁棒方法提出了一种新的分布式预测控制方法。文中，考虑稍简单于文献[16]的系统，提出一种分布式预测控制综合方法。该方法与文献[16]的区别如下。

1)文献[16]采用的约束(见该文中式(8)～(10))具有相容性约束的作用，且是固定的；而文中给出了明确的相容性约束并在线收紧此约束，故在系统演化过程中，文中的相容性约束带来的保守性更小；

2)文献[16]离线固定了收紧的状态和输入约束序列；而文中状态和输入约束是在线收紧、更新的，故在系统演化过程中约束收紧带来的保守性更小；

3)文献[16]针对标称系统在线优化性能指标；而本则针对真实系统在线优化性能指标，故文中的控制性能更优。

1 问题描述

考虑包含ns个动态耦合子系统的大规模系统，其由如下线性时不变方程描述

(1)

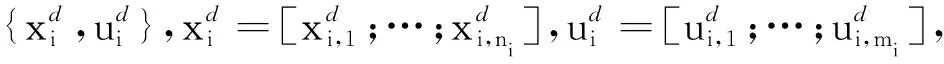
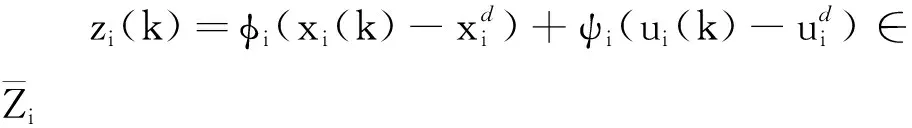
(2)

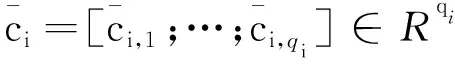
(3)

对于动态耦合子系统的分布式预测控制，每个子系统i仅知道其动态上游邻居j的假设预测轨迹，而真实预测轨迹则是未知的。故真实预测轨迹和假设预测轨迹之间存在不确定性偏差，该偏差需要通过施加约束进行处理。下节将给出动态耦合子系统的分布式预测控制综合方法。

2 分布式预测控制

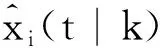
(4)

子系统i的状态预测方程为

xi(0|k)=xi(k)

(5)

文中，为u(k)的最优解添加了修正项，即实际施加到系统的控制输入为

(6)

其中κij为离线确定的反馈增益。

2.1 物理约束收紧

(7)

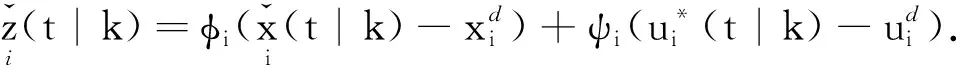
(8)

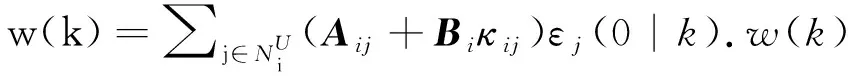
为满足约束(2)，在线优化过程中需满足如下物理约束

(9)

为收紧约束(9)以抑制不确定性偏差w(k)，首先需要通过下式约束εi(t|k)

(10)

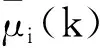
(11)

收紧后的可容许集Zi(t|k)可由下式迭代获得

ψiκi(t))Li(t)×(Aij+Biκij)Ej(k)}

(12)

其中，Li(t+1)=(Aii+Biκi(t))Li(t)，t∈{0,…,N-1} ，Li(0)=I，κi(t)为离线确定的反馈增益。

通过适当的集合运算，收紧后的可容许集Zi(t|k)等价于

(13)

其中ci(t|k)={ci,1(t|k);…;ci,qi(t|k)}为收紧的约束界向量，其确定方式为

2.2 个体终端域

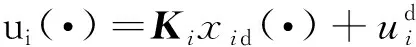
(14)

zi(t|k)∈Zi(Mi|k),i∈Ns

(15)

xi(t+1|k)∈Ωi,i∈Ns

(16)

式中x∑d(·)=[xid(·)；…；xnsd(·)]，P=diag[P1,…,Pns],Q=diag[Q1,…,Qns],K=diag[K1,…,Kns],R=diag[R1,…,Rns].

对式(14)，终端权重矩阵Pi和控制律Ki(i∈Ns)可通过求解如下优化问题确定

(17)

式中X=σP-1，Y=KX.该优化问题可通过MATLAB软件的LMI工具箱求解。式(15)～(16)成立的充分条件为

‖xid(t|k)‖Pi≤δi,t≥N,i∈Ns

(18)

式中，标量δi满足

(19)

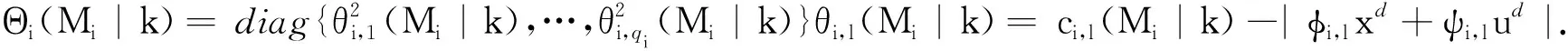
‖xid(t+1|k)‖Pi-‖xid(t|k)‖Pi≤0,t≥N,i∈Ns

(20)

应用三角不等式得

‖xid(t+1|k)‖Pi=

因此，式(20)可由下式保证

(21)

综上所述，个体终端约束可描述为

(22)

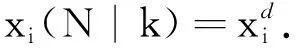
(23)

此优化问题仅在离线阶段求解(见算法1)。

2.3 相容性约束

限制假设预测轨迹和真实预测轨迹间的不确定性偏差需用到相容性约束(见文献[5]和文献[10])，该约束被施加到各子系统的优化问题可确保每个子系统(智能体)不偏离其假设轨迹过远。文中得约束(10)即为相容性约束。

据2.1节所述，物理约束的满足依赖于相容性约束(10)，因此，保证约束(10)在每个时刻k均被满足是基本前提。瓷锤再次应用约束收紧技术来收紧约束(10)，具体为

(24)

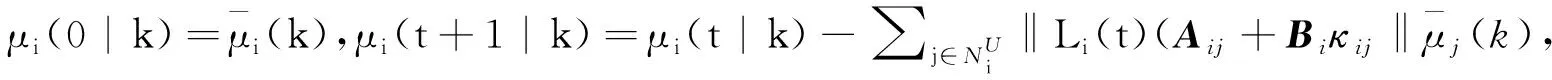
为保证整个系统的递归可行性，进而保证整个系统的闭环稳定性，为整个系统选取如下Lyapunov函数

(25)

在k+1时刻，可取如下可行输入

(26)

由该输入得到可容许(可行)状态(更多细节可参见定理1的证明部分)，如下

(27)

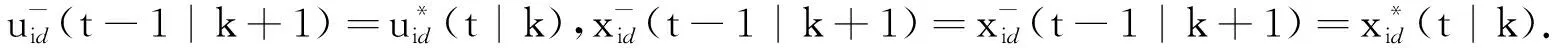
(28)

即，整体闭环系统的渐近稳定性是可以保证的。

基于上述推导，试图将相容性约束界单调减小至零，同时考虑到相容性约束(24)的递归可行性，给出以下相容性约束界的更新方程

(29)

应用此方程可得ci,l(t|k)≤ci,l(t|k+1)，μi(t|k)≤μi(t|k+1),i∈Ns，l∈{1，…，qi}，t∈{0,1,…,N-1}，k≥0.故有

Ei(k)⊇Ei(k+1),i∈Ns,k≥0

(30)

Zi(s|k)⊆Zi(s|k+1),s∈{0,…,N-1},k≥0

(31)

注释1：文献[16]采用tube-based方法来收紧初始状态(输入)约束，其依赖于某一固定的集合；文中则基于一系列递减的集合Ei(k)来收紧初始约束，这一方式可降低系统可容许集的保守性(见仿真部分)。

3 主要结果及整体算法

3.1 主要结果

通过加入前述各节中给出的约束，可得每个子系统i的优化问题如下

s.t. (7)，(11)，(22)，(24)

(32)

主要结果由下述定理阐述

定理1：如果每个子系统i的优化问题(32)在k=0时刻是可行的，那么，在每个时刻求解该优化问题并实施控制输入(6)，可保证

1)在k>0时刻，每个子系统的优化问题(32)均是可行的；

2)在k≥0时刻，物理约束(2)均满足；

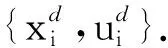
证明

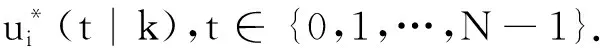
(33)

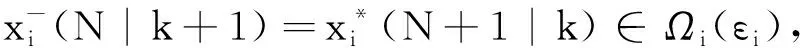
(34)

进一步地，根据收紧后的相容性约束(24)和更新方程(29)可得

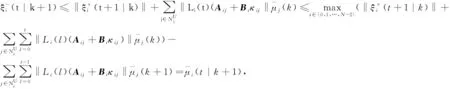
(35)

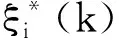
3.2 分布式预测控制算法

算法1(分布式预测控制整体算法)：

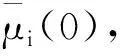
BiKi)txi(0),t∈{0,…,N-1}.

在线阶段：初始化，k=0时，对子系统i

2)计算ci(t|0)和μi(t|0)；

重复执行：在k>0时，针对每个子系统i

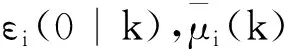
在算法1的离线阶段，反馈增益κij和κi(t)可由优化问题(36)获得

s.t.‖Li(Mi)‖=0

(36)

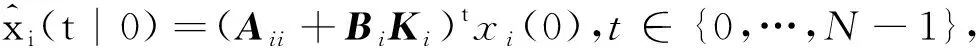
4 仿 真

采用文献[23]中的系统，该系统由ns=3个弹簧-阻尼小车相互连接而成。系统动态为

式中xi,1，xi,2和ui(i∈Ns)分别为各子系统i的位移，m;速度,m/s和控制输入,N；k0=1.05 N/m为非线性弹簧的稳态刚度系数；kc=0.01 N/m为各子系统互联的线性弹簧的稳态刚度系数；hd=0.3 Ns/m为每个小车的阻尼系数；m=1.5 kg为每个小车的质量。

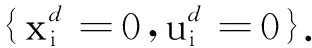
为证明文中算法(表示为情形2，case 2)的有效性，此处将给出文献[16](表示为情形1，case 1)中算法的比较。对于情形2，取Q=diag{Q1,Q2,Q3},R=diag{R1,R2,R3}，其中，Qi=diag[15,15]，Ri=1；终端权重矩阵和反馈增益分别为

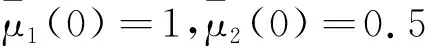
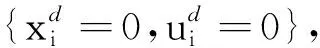
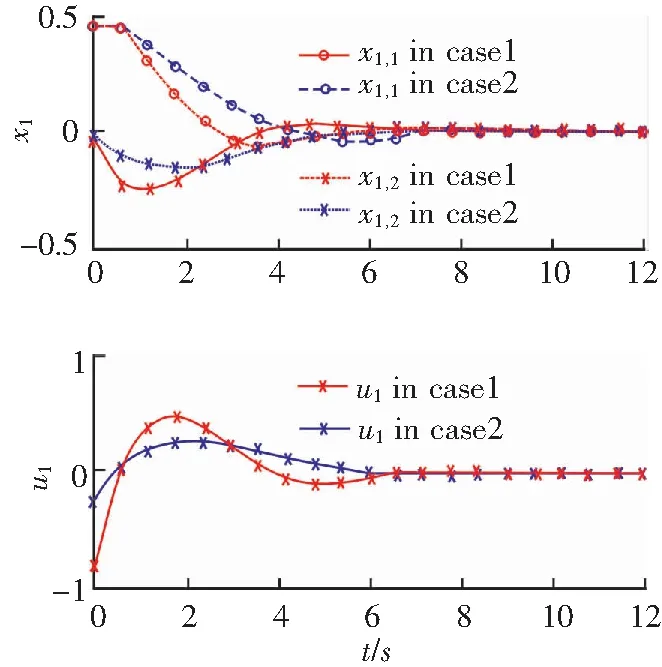
图1 子系统1的状态和输入轨迹Fig.1 State and input trajectories of subsystem 1

图2 子系统2的状态和输入轨迹Fig.2 State and input trajectories of subsystem 2

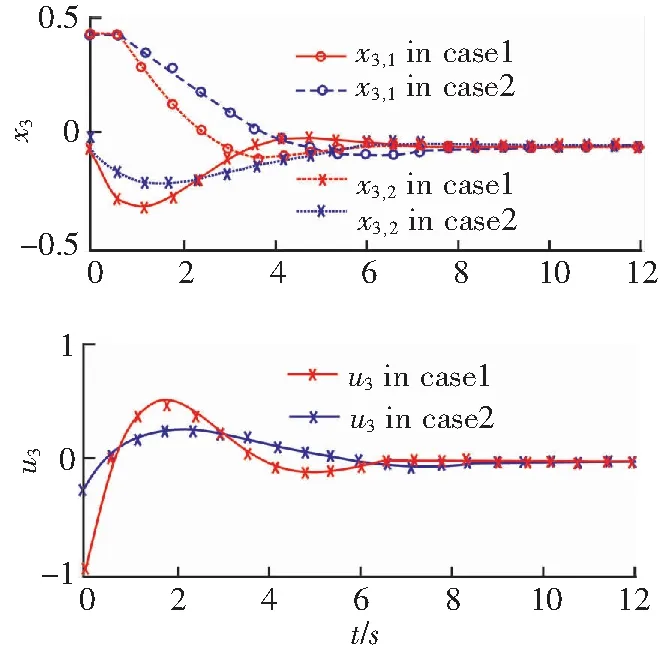
图3 子系统3的状态和输入轨迹Fig.3 State and input trajectories of subsystem 3

图4 情形1，2的优化时间比较Fig.4 Optimization time comparisons between case 1 and 2

(37)

经计算，情形1，2中的性能指标Jsum分别为8.12和4.75.故情形2的控制性能远优于情形1.

仿真执行的软硬件环境为：台式机(CPU：Intel Core i3，2.93 GHz；RAM：4 G)；MATLAB 2012 LMI工具箱以及Multi-Parametric工具箱。LMI工具箱用于求解各个优化问题；Multi-Parametric工具箱用于执行相关的集合运算。

5 结 论

1)针对若干动态耦合子系统组成的大规模系统提出了一种分布式预测控制综合方法。在分布式预测控制策略中，每个子系统必须采用其邻居的假设预测状态轨迹，此轨迹有别于真实预测状态轨迹。通过将前述区别视作不确定性，并进一步考虑以下因素，给出分布式预测控制综合方法；

2)考虑动态耦合特性，针对每个子系统给出了解耦的个体终端域，此终端域具有正不变性；为保证整体系统递归可行性和闭环稳定性，采用收紧的相容性约束来抑制不确定性偏差；

3)最后，针对每个子系统建立优化问题，并给出便于实施的分布式预测控制算法。

参考文献(References)：

[1] 席裕庚，李德伟，林 姝.模型预测控制——现状与挑战[J].自动化学报，2013，39(3)：222-236.

XI Yu-geng，LI De-wei，LIN Shu.Model predictive control：status and challenges[J].Acta Automatica Sinica，2013，39(3)：222-236.

[2] 席裕庚，李德伟.预测控制定性综合理论的基本思路和研究现状[J].自动化学报，2008，34(10)：1225-1234.

XI Yu-geng，LI De-wei.Fundamental philosophy and status of qualitative synthesis of model predictive control[J].Acta Automatica Sinica，2008，34(34)：1225-1234.

[3] 李少远.工业过程系统的预测控制[J].控制工程，2010，17(4)：4-12.

LI Shao-yuan.Model-based predictive control for industrial process-a survey[J].Control Engineering of China，2010，17(4)：4-12.

[4] Christofides P D，Scattolini R，de la Pena D M，et al.Distributed model predictive control：a tutorial review and future research directions[J].Computers and Chemical Engineering，2013，51(4)：21-41.

[5] Dunbar W B，Murray R M.Distributed receding horizon control for multi-vehicle formation stabilization[J].Automatica，2006，42(4)：549-558.

[6] Kuwata Y，Richards A，Schouwenaars T，et al.Distributed robust receding horizon control for multivehicle guidance[J].IEEE Transactions on Control Systems Technology，2007，15(4)：627-641.

[7] Venkat A N，Hiskens I A，Rawlings J B，et al.Distributed MPC strategies with application to power system automatic generation control[J].IEEE Transactions on Control Systems Technology，2008，16(6)：1192-1206.

[8] Zheng Y，Li S Y，Wang X B.Distributed model predictive control for plant-wide hot-rolled strip laminar cooling process[J].Journal of Process Control，2009，19(9)：1427-1437.

[9] 夏圈世,俞金寿,蒋慰孙.大规模工业过程系统的优化控制策略[J].控制与决策,1987(1):54-59.

XIA Quan-shi,YU Jin-shou,JIANG Wei-xun.The optimization control stategy of large-scale industrial process system[J].Control and Decision,1987(1):54-59.

[10] Ding B C，Xie L H，Cai W J.Distributed model predictive control for constrained linear systems[J].International Journal of Robust and Nonlinear Control，2010，20(11)，1285-1298.

[11] Wang C，Ong C J.Distributed model predictive control of dynamically decoupled systems with coupled cost[J].Automatica，2010，46(12)，2053-2058.

[12] Acar L.Boundaries of the receding horizon control for interconnected systems[J].Journal of Optimization Theory and Applications，1995，84(2)，251-271.

[13] Venkat A N，Rawlings J B，Wright S J.Plant-wide optimal control with decentralized MPC[J].IFAC Proceedings Volumes，2004，37(9)：589-594.

[14] Jia D，Krogh B.Min-max feedback model predictive control for distributed control with communication[C]//Proceedings of the 2002 American Control Conference，2002(6)：4507-4512.

[15] Dunbar W B.Distributed receding horizon control of dynamically coupled nonlinear systems[J].IEEE Transactions on Automatic Control，2007，52(7)：1249-1263.

[16] Farina M，Scattolini R.Distributed predictive control：a non-cooperative algorithm with neighbor-to-neighbor communication for linear systems[J].Automatica，2012，48(6)：1088-1096.

[17] Mayne D Q，Seron M M，Rakovic S V.Robust model predictive control of constrained linear systems with bounded disturbances[J].Automatica，2005，41(2)：219-224.

[18] Richards A，How J P.Robust distributed model predictive control[J].International Journal of Control，2007，80(9)：1517-1531.

[19] Chisci L，Rossiter J A，Zappa G.Systems with persistent disturbances：predictive control with restricted constraints[J].Automatica，2001，37(7)：1019-1028.

[20] Richards A，How J.Robust stable model predictive control with constraint tightening[C]//2006 American Control Conference，2006：1557-1562.

[21] Scokaert P O M，Mayne D Q.Min-max feedback model predictive control for constrained linear systems[J].IEEE Transactions on Automatic Control，1998，43(8)：1136-1142.

[22] Casavola A，Giannelli M，Mosca E.Min-max predictive control strategies for input-saturated polytopic uncertain systems[J].Automatica，2000，36(1)：125-133.

[23] Liu X T，Shi Y，Constantinescu D.Distributed model predictive control of constrained weakly coupled nonlinear systems[J].Systems and Control Letters，2014，74：41-49.