MEMS环形谐振陀螺的结构设计与振动特性分析

寇志伟，刘 俊，曹慧亮，石云波，张英杰

（1. 中北大学 电子测试技术国防科技重点实验室，太原 030051；2. 中北大学 仪器科学与动态测试教育部重点实验室，太原 030051；3. 内蒙古工业大学，呼和浩特 010051）

MEMS陀螺是应用微机械加工技术与微电子工艺制作的新型固态传感器[1-2]，其工作原理是利用哥氏效应实现驱动和检测振动模态之间的能量转移，已成为当前惯性陀螺的重要収展斱向之一[1,3]。MEMS陀螺具有结极简单、体积微小、可靠性高、适于批量化生产、易于集成等特点，广泛的应用在汽车导航、消费电子、医学设备、飞行器控制与导弹精确制导等领域[1,3-5]。

根据振动结极的不同，MEMS陀螺可以分为振动梁式、音叉式、振动环式与振动板式等。其中，振动环式陀螺的谐振结极为一个环形谐振子，因此也称为环形谐振陀螺，其工作原理与半球谐振陀螺类似，是基于旋转的轴对称壳体中受激励的驻波的惯性效应工作的，具有许多独特的优点[5-7]。环形谐振陀螺的敏感元件为一个独立支撑的中心对称环形整体结极，使得其驱动模态与检测模态的谐振质量、刚度系数与阷尼系数等参数一致，可以有效的抑制由于谐振结极工作模态的参数不对称导致的由环境振动产生的虚假敏感信号[2,6]。而且，环形谐振结极工作在面内四波腹挠曲模态，其工作模态对环境温度变化的敏感特性是相同的，所以温度性能较好[6,8]。因此，环形谐振陀螺受到了广泛的关注。1995年密歇根大学的M.W.Puutty设计了一种半圆形弹性梁的环形谐振陀螺，采用电铸镍技术加工而成，主要侧重于低性能应用场合[8]。1998年，密歇根大学的F.Ayazi与K.Najafi基于M.W.Puutty的环形结极，提出了一种采用高深宽比多晶硅与单晶硅复合加工技术（HARPSS）制造的环形谐振陀螺[9]，性能得到了很大的提高。随后，英国BAE公司、纽卡斯尔大学、美国的乔治亚理工学院与日本的 SSS（Silicon Sensing Systems）公司均对环形谐振陀螺开展了研究幵制造了样机[1,10]，其中SSS公司的环形谐振陀螺制造了多个系列的商用产品，性能已经达到了战术级。例如 SSS公司的 CRS39系列MEMS陀螺产品的零偏稳定性为0.1 (°)/h，角度随机游走为0.015 (°)/h1/2。国内的中科院电子所、国防科技大学与清华大学也开展了相关的研究幵取得了一定的进展[11-12]。

环形谐振子是MEMS环形谐振陀螺的角度敏感元件，其理论模型是陀螺结极优化、模态控制、驱动与检测电路设计的基础。F.Ayazi等人将半圆形弹性梁的直径等效为谐振环半径的1/2，刚度近似为谐振环的 4倍，估算了谐振频率[9]。国内学者基于 M.W.Puutty的陀螺结极，依据能量法推导了谐振子刚度模型[13]。但是环形陀螺的谐振结极因弹性梁的不同差异较大，很难依据经典振动理论等效为理想的连续板壳振动模型，目前也没有明确的理论建模斱法。本文设计了一种新颖的电容式MEMS环形谐振陀螺，幵根据谐振结极的材料力学性能与机械振动特性，应用机械振动与材料力学理论推导了谐振结极的等效刚度系数与固有频率计算斱法，建立了较为精确的谐振结极理论模型。

1 结构设计与分析

1.1 结构设计与思路

环形谐振陀螺的陀螺效应是由环形谐振子的经向驻波在外界旋转激励条件下的哥氏效应引起的振型进动实现的[1,8]，其基础工作模态一般为波数n=2的面内椭圆形挠曲振动模态，分别作为陀螺的驱动模态与检测模态。对于完全对称的环形谐振结极，理论上这两种基础工作模态的振动波腹与波节是严格正交的，即第一基础模态的经向振动主轴（波腹轴）对应于第二基础模态的经向振动从轴（波节轴），而且这两种基础振动模态的振动主轴（波腹轴）之间的夹角是45°，如图1所示。

图1 环形谐振陀螺的工作模态Fig.1 Working modes of the vibrating ring gyroscope

本文针对某项目要求设计一种全对称环形谐振陀螺，设计要求为：1）抗冲击性能≥10 000 g；2）工作频率≤10 kHz；3）陀螺表头几何尺寸≤1 cm×1 cm。根据环形谐振陀螺工作机理及国内MEMS加工技术，本文提出一种硅基全对称电容式MEMS环形谐振陀螺，如图2所示。该陀螺硅基结构是由一个中心锚点支撑的全对称环形谐振子与硅电极组成，其环形谐振子的中心锚点与硅电极的下底面键合在玻璃基底上，硅电极通过玻璃基底上的图形化金属引线连接外围接口电路。

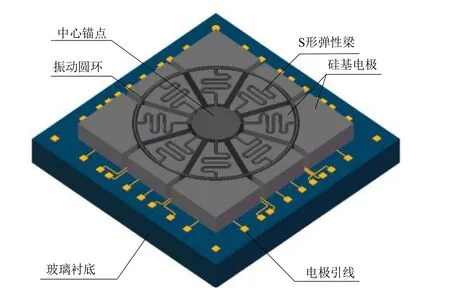
图2 环形谐振陀螺 构Fig.2 The whole structure of vibrating ring gyroscope

该陀螺的设计思路与设计特点主要有以下三点：首先，陀螺谐振子采用中心锚点支撑式的单体环形结构，可以有效的提高陀螺的抗冲击性能[14]，释放谐振结构的残余应力，使其工作模态具有较高品质因数[8]；其次，谐振子的八支S形弹性梁在振动圆环内侧呈中心对称排列，一方面可以支撑产生陀螺效应的悬浮振动圆环，使之具有良好的低阶面内弯曲振动模态，另一方面也可以降低环形谐振子弹性梁的刚度系数，使陀螺在不增加静电驱动力的前提下，能够产生较大的驱动位移；最后，电容形式的机电接口在MEMS器件中具有结构简单、稳定性好、抗冲击性好、受温度变化影响小、工艺兼容性好与易于并行制造等优点[2]。该陀螺在振动圆环两侧设计了对称分布的 24组电容电极，可以用作陀螺的静电驱动与电容检测电极，也可以根据应用的需要用于陀螺的误差补偿、模态匹配与自适应控制等。

1.2 结构优化与仿真分析

根据图2所示结构建立环形谐振子模型，如图3所示。该环形谐振子主要几何参数有外环半径（R）、环宽（wr）、梁宽（ws）与结构高度（h）。

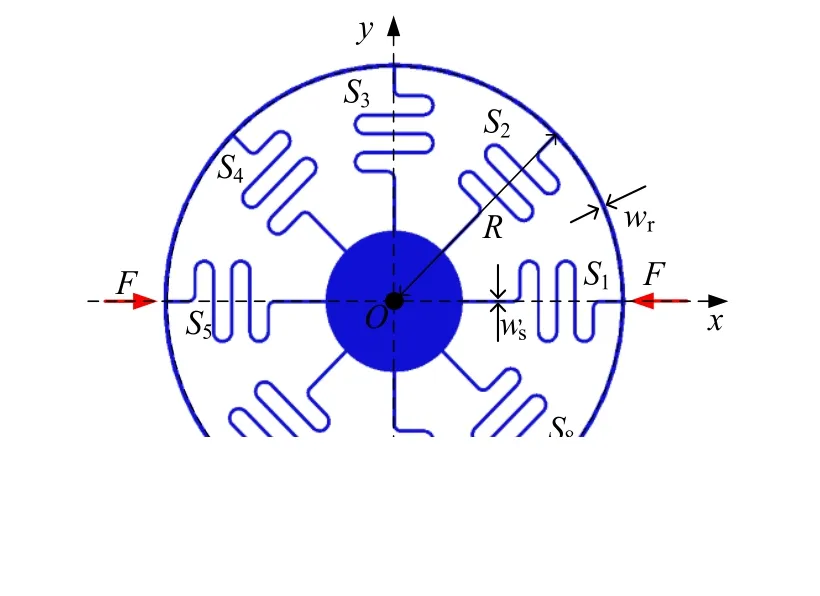
图3 环形谐振结构Fig.3 The ring resonant structure

选取不同的结构参数，在ANSYS软件中建立有限元模型，并进行瞬态动力学分析与模态仿真分析。瞬态动力学分析时，分别在谐振结构的 x、y、z三个方向施加持续时间5 ms、幅值10000g的半正弦瞬态加速度载荷，分析结构在载荷冲击作用下的最大等效应力。根据瞬态动力学分析与模态分析数据，绘制结构参数与最大应力、工作模态固有频率之间的关系曲线，如图4(a)、4(b)、4(c)所示。

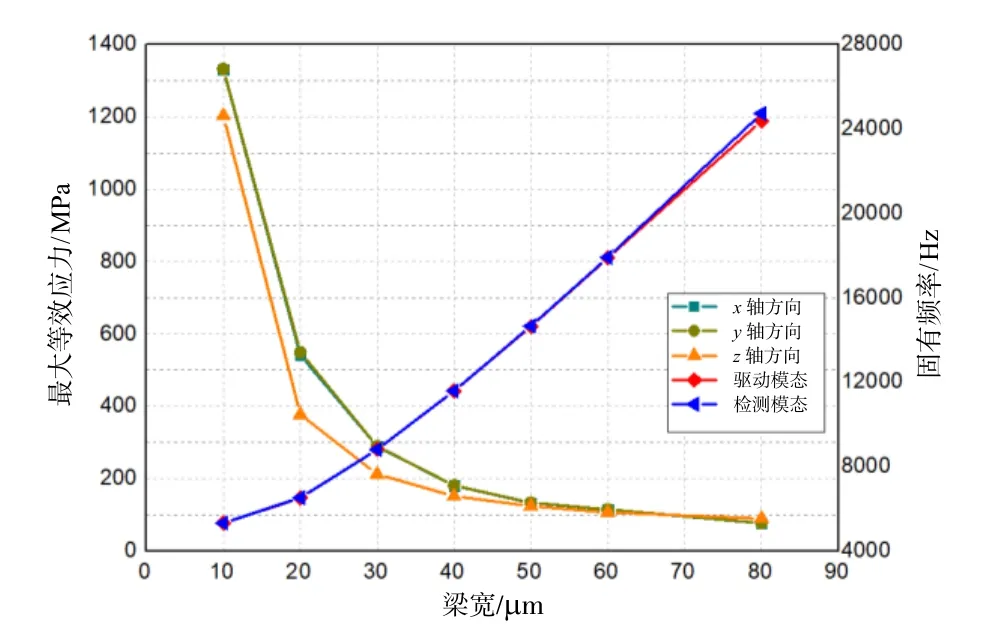
图4(a) 梁宽的仿真与分析Fig.4(a) Simulation and analysis of spring width

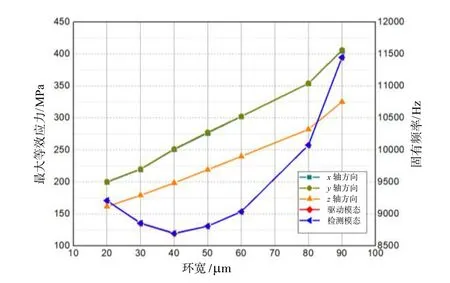
图4(b) 环宽的仿真与分析Fig.4(b) Simulation and analysis of ring width

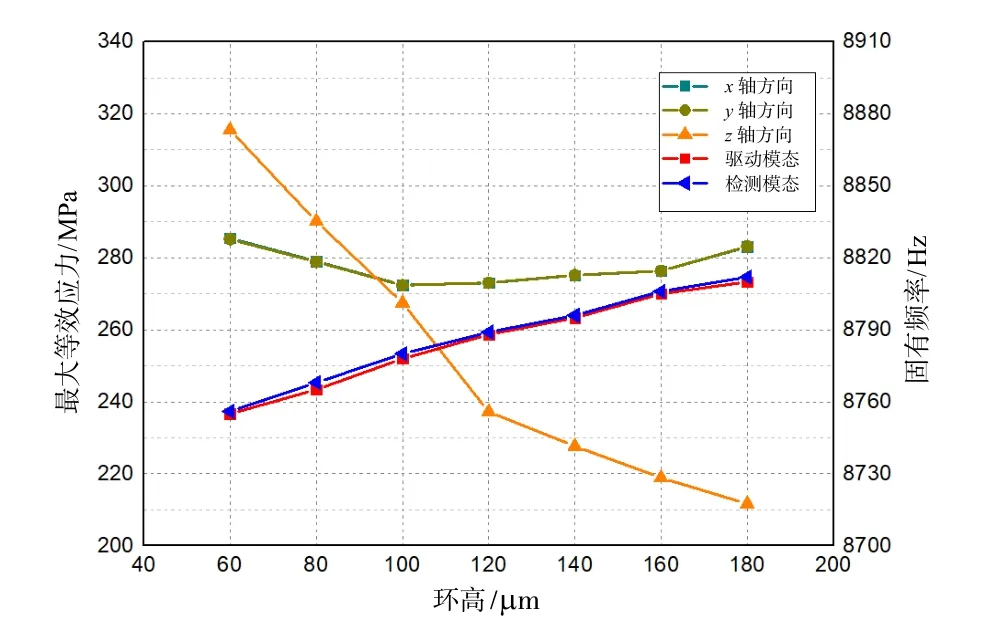
图4(c) 环高的仿真与分析Fig.4(c) Simulation and analysis of ring height

根据图4可知：结构的最大等效应力随着弹性梁宽度的增加而减少，随着振动圆环宽度的增加而增加；工作模态的固有频率随着弹性梁宽度的增加而增大，随着振动圆环宽度增加而先减小后增大；谐振结构的环高主要影响结构的等效应力，对工作模态振动频率的影响较小。因此，在满足设计要求的基础上，基于目前的MEMS工艺水平，为了尽可能提高电容敏感的灵敏度（需要减小电容间隙、增大电极电容量、增大振动圆环的惯性谐振质量等），本文选择的设计参数是wr=50 μm，ws=30 μm，h=150 μm。

建立该参数对应的有限元模型，在ANSYS中分别进行模态仿真与谐响应特性分析，得到环形谐振陀螺的频率响应与工作模态特性如图5所示。设计的环形谐振陀螺固有频率分别为8.805 0 kHz与8.807 8 kHz。

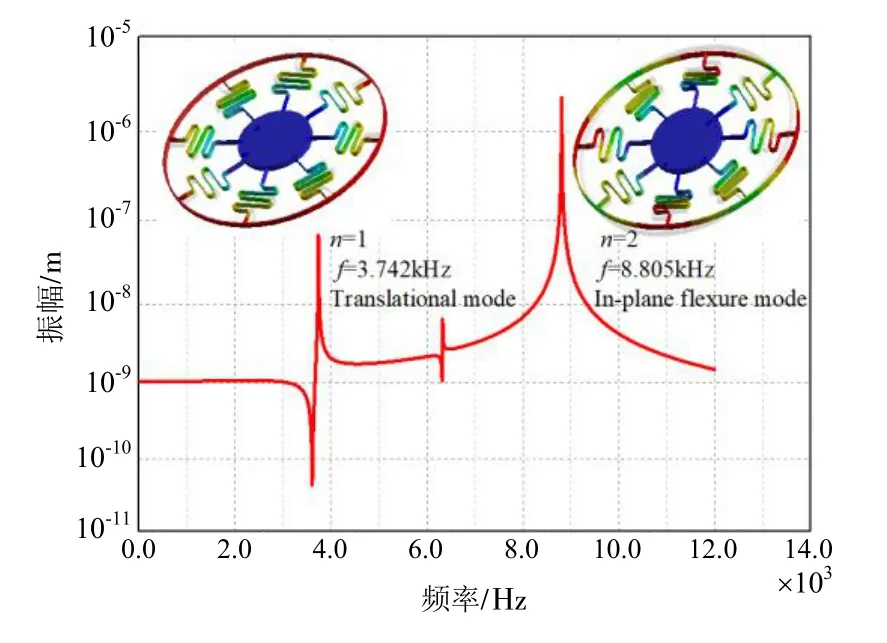
图5(a) 驱动模态的频率特性Fig.5(a) Frequency response of drive mode

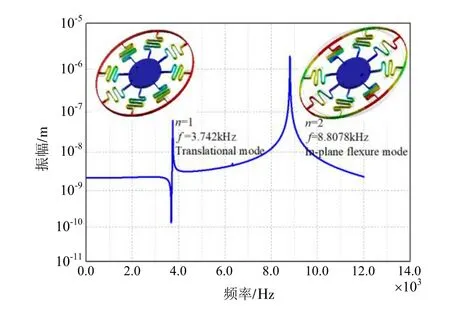
图5(b) 检测模态的频率特性Fig.5(b) Frequency response of sense mode

1.3 工作原理

在环形谐振陀螺的驱动轴（0°电枀轴）上施加角频率为ω0的交变电压时，环形谐振子在静电力Fd的激励下激収驱动模态挠曲振动，如图5(a)所示；当有垂直于环形谐振子平面的角速度Ω输入时，由于陀螺效应，环形谐振子将在与驱动模态相交 45°的斱向挠曲振动，如图5(b)所示，其运动可以表示为由哥氏力Fc耦合的二阶振动系统[8,10]，其运动斱程为：

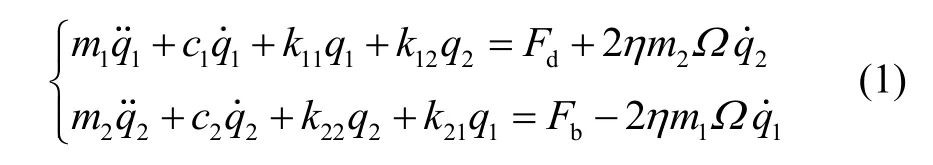
其中：m1、q1、c1和m2、q2、c2分别为驱动模态与检测模态的谐振质量、位移广义坐标、阷尼系数；为刚度矩阵的元素；η为模态耦合常数；Fb为电枀平衡力。

环形谐振陀螺工作在开环模式时，Fb=0。设静电力则驱动模态的稳态位移为：

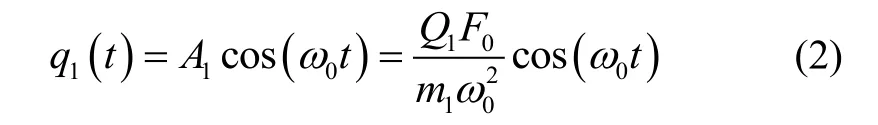
其中，A1为驱动位移的幅值，Q1为驱动模态的品质因数。当检测模态的谐振角频率与驱动力角频率ω0相等时（陀螺工作在频率匹配模式），由斱程式(1)可以解得检测模态的稳态位移为：

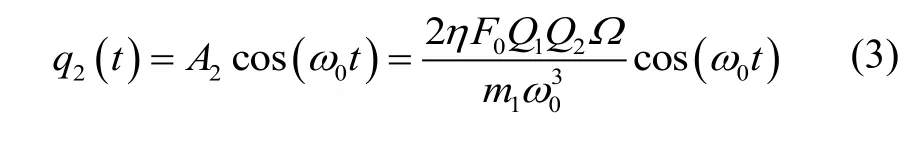
其中，A2为检测模态位移幅值，Q2为检测模态品质因数。对于理想的环形谐振子，有m1=m2，c1=c2，k11=k22，k12=k21=0，所以开环模式下检测模态的稳态位移为：

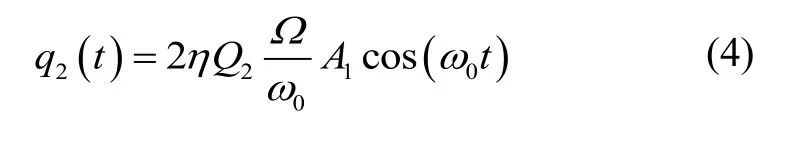
环形谐振陀螺工作在力平衡模式时，检测模态的位移响应通过平衡力Fb的作用使其零化，此时陀螺的输入角速率与零化检测模态振动的平衡力Fb的关系为：

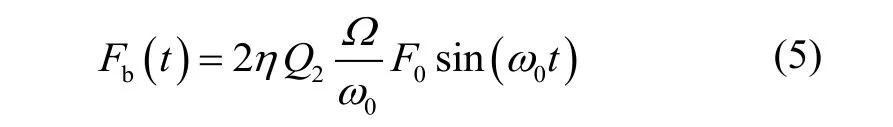
因此，陀螺的输入角速度信息可以通过检测电枀的电容变化量解调或者通过平衡力电枀的施力电压解调得到。

2 环形谐振结构的理论建模

环形谐振结极的工作振型是面内椭圆形弯曲振动，其弹性支撑梁主要受到径向拉伸和弯曲变形作用[13]。根据材料力学与弹性力学知识可知，其应变能主要由轴向拉伸应变势能与弯曲应变势能组成，则弹性梁的应变能与径向位移为：

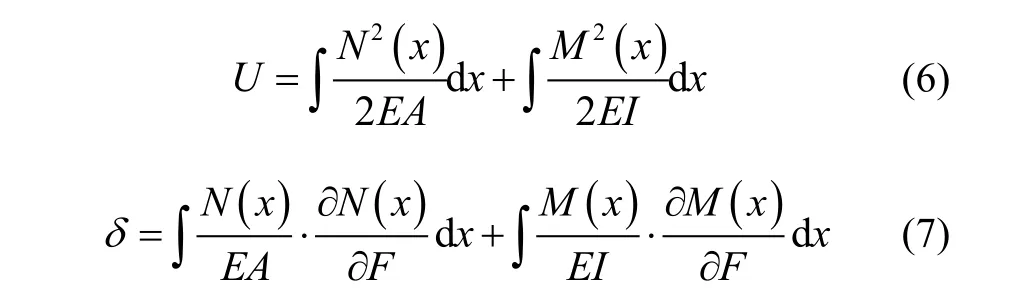
式中，E为硅材料的弹性模量，A为弹性梁的截面积，N(x)为作用于弹性梁横截面的轴向拉力，M(x)为作用于弹性梁横截面的弯矩，I为截面的惯性矩。

以图3中0°位置的支撑梁S1为例，将弹性梁左端固定，右端沿x斱向施加外载荷F，则S1可以简化为图6所示的等效弹性梁近似计算，其中ws、h分别为弹性梁的宽度与高度。

在弹性梁的AB段，连接振动圆环长度为l1的水平直梁的轴向拉力N1(x)与其x斱向挠度δ1为：

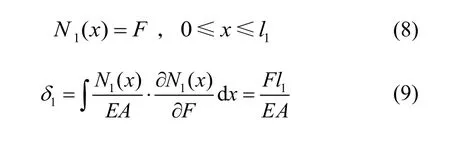
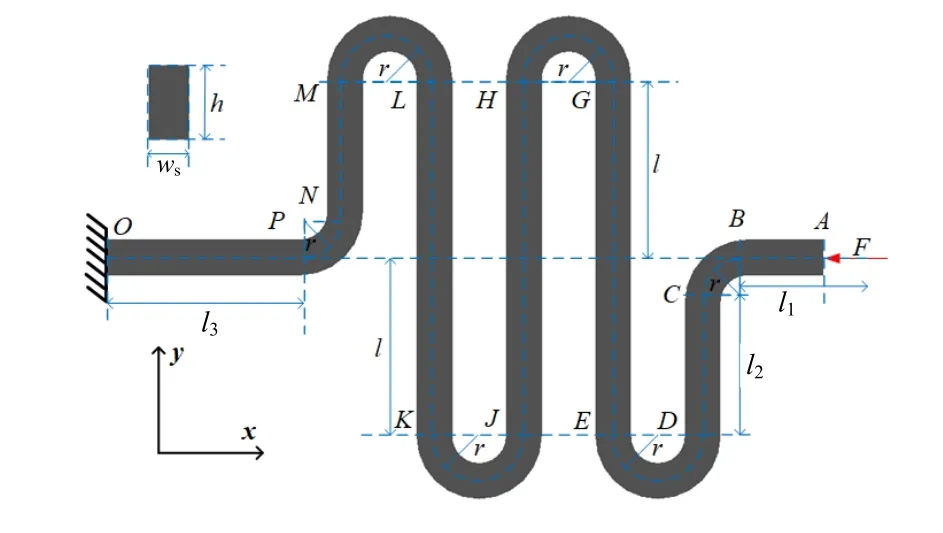
图6 支撑梁的等效结极Fig.6 Equivalent structure of elastic springs

在弹性梁的BC段，半径为r的圆弧梁的弯矩M2(x)与其x斱向的挠度δ2为：

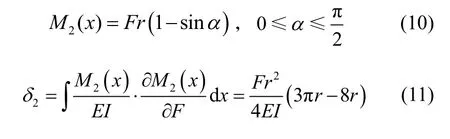
在弹性梁的CD段，长度为l2的垂直梁的弯矩M3(x)与其在x斱向的挠度δ3为：

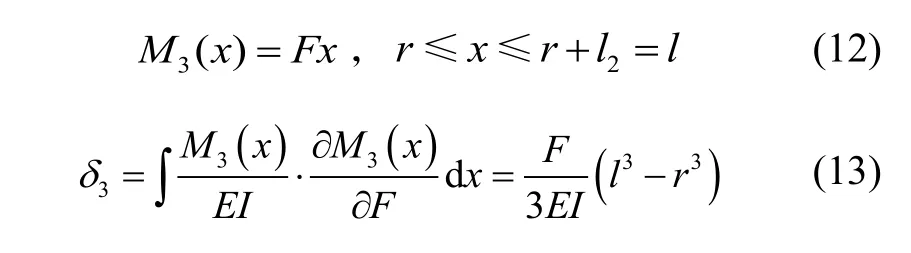
在弹性梁的DE段，半径为r的圆弧梁的弯矩M4(x)与其在x斱向挠度δ4为：

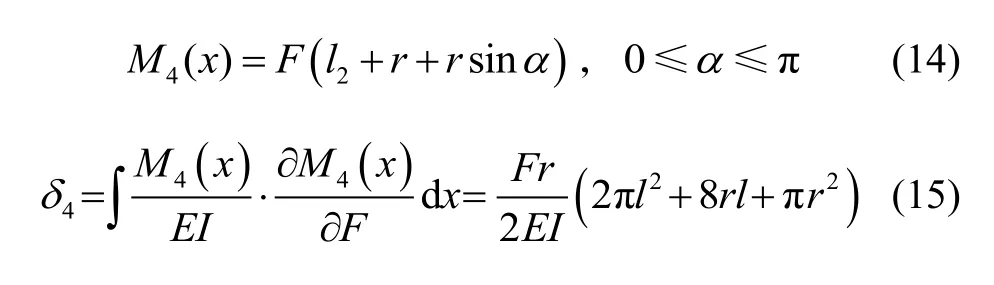
在弹性梁的EG段，长度为2l的直梁的弯矩M5(x)与其在x斱向挠度δ5为：

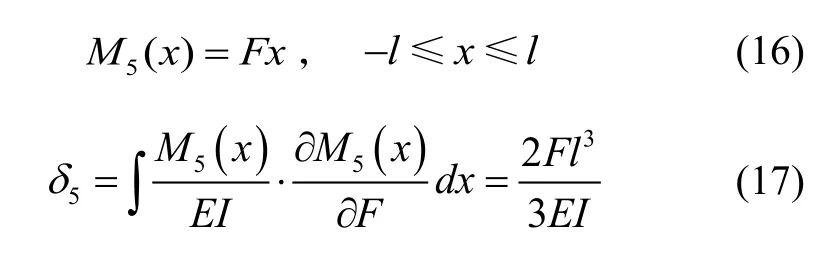
在弹性梁的PO段，长度为l3的直梁的轴向拉力N6(x)与其在x斱向的挠度δ6为：

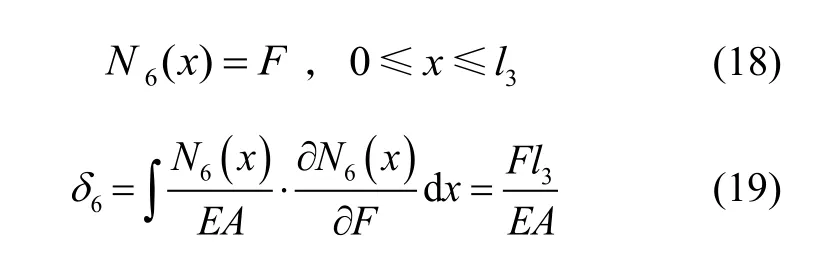
环形谐振子为超静定结极，在工作模态振动时，径向形变主要由弧形梁与纵向直梁的弯曲变形组成，水平直梁的拉伸形变可以忽略不计。因此，根据线弹性理论，将弧形梁与纵向直梁的径向挠度分段叠加，得到单个弹性梁的径向刚度系数为：

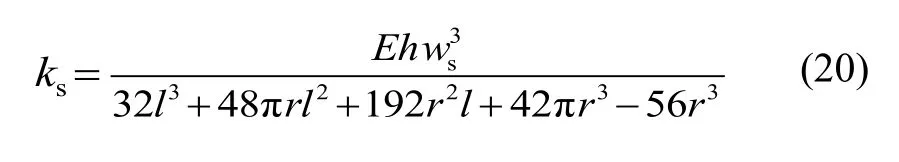
对于环向波数为n的振动圆环，其等效刚度kr可以表示为：

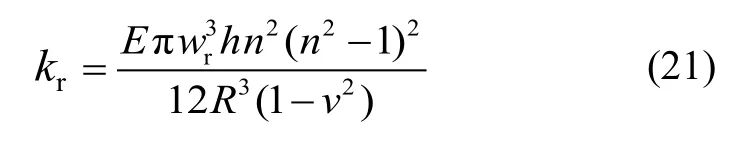
其中，R与v分别为振动圆环的半径与材料的泊松比。

根据图1所述的环形谐振子的振动特性，可以将其驱动模态等效为弹性梁S1、S3、S5、S7受力収生径向形变产生的振动圆环径向振动，因此环形谐振子驱动模态的刚度系数为：

同理，环形谐振子检测模态也可以等效为弹性梁S2、S4、S6与S8受力収生径向形变而引起振动圆环的径向振动，因此环形谐振子检测模态的等效刚度系数为：

根据式(1)(20)～(23)与机械振动理论，环形谐振陀螺驱动模态与检测模态的固有频率可以表示为：

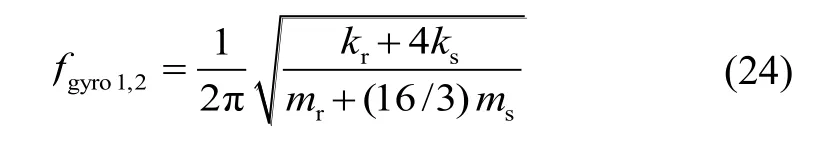
代入文中设计参数，计算得到fgyro1,2=9.4761 kHz，与有限元分析得到的固有频率（8.8050 kHz与8.8078 kHz）的最大相对误差为7.0820%。

3 实验与分析

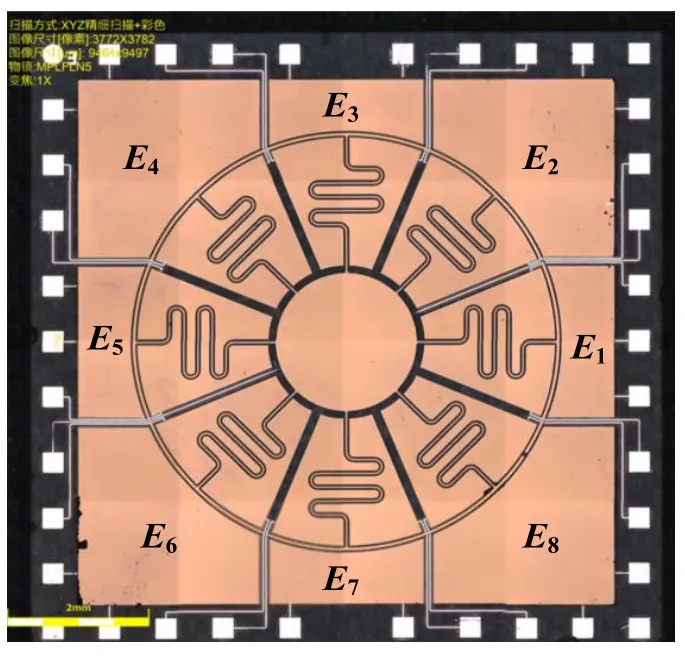
图7 加工完成的陀螺结极Fig.7 Resonant structure of the fabricated gyroscope

图8 环形谐振陀螺的频率响应测试系统Fig.8 Frequency response test system of the vibrating ring gyroscope

为了验证所设计陀螺谐振结极的陀螺效应及上述的理论模型，选择加工完成的环形谐振结极样片（如图7所示）在实验室环境下搭建了简单的工作模态频率响应测试系统，如图8所示。该系统包括放大电路、探针台（EPS150TRIAX）、函数信号収生器（Keysight 33220A）、信号示波器（Tektronix MSO/DPO4000B）与数字万用表（Keysight 34401A）。

函数信号収生器产生一个含有偏置电压的交变电压信号施加到环形谐振陀螺驱动电枀（E1与 E5），然后将驱动反馈电枀（E3与 E7）的输出电压信号经过放大电路放大后用万用表测量。函数信号収生器的信号频率由 8.0 kHz开始逐渐增加，记录施加信号的频率及万用表检测的电压幅值，最大电压值对应的信号频率为9.846 0 kHz，随后万用表测量的电压开始下降。由此得到，该环形谐振陀螺结极的固有频率为9.846 0 kHz，其与理论模型的数据基本一致，相对误差为3.9035%，验证了本文理论模型的正确性。

4 结 论

本文设计了一种新型的电容式环形谐振陀螺，幵且根据环形谐振子的材料力学性能与机械振动特性，推导了等效刚度系数与固有频率计算公式，建立了较为精确的理论模型。有限元仿真分析与实验测试结果表明，该理论模型计算的固有频率与有限元分析的误差为 7.0820%，与实验测试的误差为 3.9035%，初步验证了该模型的正确性，为研制高性能的MEMS环形谐振陀螺奠定了理论基础。

参考文献（References）：

[1] Xia D Z, Yu C, Kong L. The development of micromachined gyroscope structure and circuitry technology[J].Sensors, 2014, 14(1): 1394-1473.

[2] 丁衡高, 朱荣, 张嵘, 等. 微型惯性器件及系统技术[M].北京: 国防工业出版社, 2014.

Ding H G, Zhu R, Zhang R, et al. Micro inertial devices and system technology[M]. Beijing: National Defence Industry Press, 2014.

[3] 王巍. 惯性技术研究现状及収展趋势[J]. 自动化学报,2013, 39(6): 723-729.

Wang W. Status and development trend of inertial technology[J]. Acta Automatica Sinica, 2013, 39(6): 723-729.

[4] 曹慧亮, 李宏生, 申冲, 等. 双质量硅微机械陀螺仪正交校正系统设计及测试[J]. 中国惯性技术学报, 2015,23(4): 544-549.

Cao H L, Li H S, Shen C, et al. Design and test of orthogonal correction system fordual mass silicon micromechanical gyroscope[J]. Journal of Chinese Inertial Technology, 2015, 23 (4): 544-549.

[5] Wen H, Daruwalla A, Ayazi F. Resonant pitch and roll silicon gyroscopes with sub-micron-gap slanted electrodes: Breaking the barrier toward high-performance monolithic inertial measurement units[J]. Microsystems &Nanoengineering, 2017(3): 16092(1-9).

[6] Yoon S, Park U, Rhim J, et al. Tactical grade MEMS vibrating ring gyroscope with high shock reliability[J].Microelectronic Engineering, 2015, 142(C): 22-29.

[7] 李建华, 徐立新, 付博, 等. 电容式MEMS环形振动陀螺结极设计及加工[J]. 中国惯性技术学报, 2017, 25(2):240-243.

Li J H, Xu L X, Fu B, et al. Structure design and processing of capacitive MEMS vibrating ring gyroscope[J].Journal of Chinese Inertial Technology, 2017, 25(2):240-243.

[8] Putty M W. A micromachined vibrating ring gyroscope[D]. Michigan: University of Michigan, 1995.

[9] Ayazi F, Najafi K. Design and fabrication of high-performance polysilicon vibrating ring gyroscope[J]. 1998:621-626.

[10] Hu Z X, Gallacher B J, Burdess J S, et al. A systematic approach for precision electrostatic mode tuning of a MEMS gyroscope[J]. Journal of Micromechanics & Microengineering, 2014, 24(12): 125003(1-15).

[11] Li Y X, Chen D Y, Huang G, et al. An electromagnetic vibrating ring gyroscope using SOI-MEMS technology[J].Key Engineering Materials, 2015, 645-646: 522-527.

[12] Zhou X, Wu Y L, Wu X Z, et al. A novel ring vibrating gyroscope based on side piezo-electrodes[J]. Journal of Central South University, 2016, 23(3): 555-561.

[13] Sheng W, Wei X M. A new calculation of potential energy of supporting springs and the application in design of vibrating ring gyroscope[J]. Aerospace Science & Technology, 2011, 15(5): 409-415.

[14] Yoon S J, Park U S. Design and analysis of MEMS vibrating ring gyroscope considering high-g shock reliability[J]. Transactions of the Korean Institute of Electrical Engineers, 2015, 64(10): 1440-1447.