基于混沌时间序列模型的危险化学品泄漏事故预测

2018-05-31赵淑琪谢饶青廖婵娟

安全与环境工程 2018年3期

赵淑琪,刘燊,谢饶青,贺蕾,周宇,廖婵娟,2

(1.湖南农业大学资源环境学院，湖南长沙 410128；2.湖南农业大学农业环境保护研究所，湖南长沙 410128)

由危险化学品(以下简称危化品)引起的灾害和事故已成为化学工业发展的重要制约因素之一，并引起了社会的广泛关注。因此，如何对危化品事故进行有效的预测和防控，一直是安全学科所面临的重大课题[1]。近些年，许多学者对危化品事故进行了预测研究，如陈程等[2]基于危化品运输事故的统计数据，利用 Spearman 秩相关系数对各影响因子进行了相关性检验，并采用ANFIS方法构建了高速公路危化品事件处置持续时间的预测模型；李建民等[3]研究了海上危化品运输系统(MDCTS)安全状态突变的原因及特点，并构建了安全评价模型,实现了对MDCTS安全状态的预测;文仁强等[4]将危化品泄漏扩散快速预测模型在应急平台中与GIS系统进行了集成，实现了危化品泄漏扩散过程在地理场景中的动态仿真推演，并生成了应急指挥决策预案。众多事故的发生常是多种因素相互作用、连锁反应的结果，而各因素之间的相互作用存在着非线性特性。危化品泄漏事故是诸多事故中的一种，与其他事故有着许多共同的特性：它们看似是随机发生的，其实事故系统内部存在着一定的规律，具有明显的混沌特性，即非线性特性[5]。而大部分传统的预测模型都忽略了事故系统的非线性特性，从而降低了模型的预测精度[6]。混沌理论是非线性理论的重要组成部分，在简单的确定性系统中，混沌运动的内在随机性的根源出自于系统自身的非线性作用，即系统内无穷多样的伸缩与折叠变换[7]。1987年，Farmer等[8]第一次提出了混沌预测，它一般适应于短期预测，而长期预测需结合其他方法进行。孙义等[9]采用混沌预测模型研究了洪水复杂的动力和非线性特征，并分析了洪水实时预报问题，提高了洪水预报的精度，从而提高了水库防洪调度的可信度。崔铁军等[10]和张洋等[11]创新性地构建了基于小波和混沌优化的算法并用于周期来压预测，为矿区巷道工作面内的安全生产提供了重要保障。

自20世纪90年代以来的研究显示，国内外已经越来越多地将混沌理论的时间序列预测模型应用到气象[12]、水文[13]、火灾预警[14]等方面，并已经取得了初步成果，但结合混沌模型对危化品泄漏事故数进行预测的研究罕有报道，大部分研究都侧重于危化品的应急救援措施及安全管理，且只能做到事后预防而无法在事前做好相关应对的准备。鉴于此，本文在对我国2010—2015年发生危化品泄漏事故的数量进行统计的基础上，基于建立的混沌时间序列模型对我国未来3年可能发生危化品泄漏事故的数量进行了预测，并得出事故数量在各个时间段的发展趋势，以为有关部门提前做好事故预防措施提供有效的决策，具有重要的理论和现实意义。

1 混沌时间序列模型的建立

混沌时间序列模型的建立主要分为获取时间序列、相空间重构、混沌特性判别和建立混沌时间序列模型等步骤，见图1。

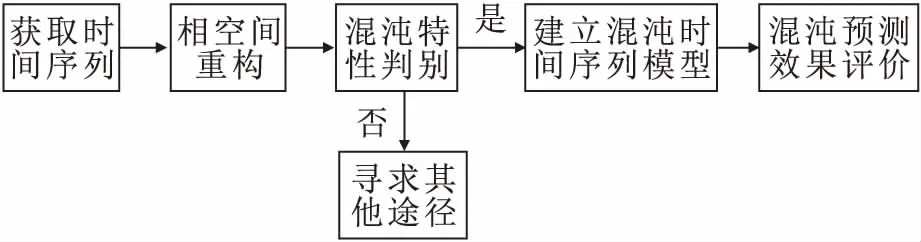
图1 混沌时间序列模型构建的步骤Table 1 Establishment prediction procedure of the chaotic time series model

1. 1 获取时间序列

本文统计了2010—2015年各月份我国发生的危化品泄漏事故数量[15](数据来源于危化品事故信息网)，并绘制成时间序列表，见表1。

表1 2010—2015年各月份我国发生的危化品泄漏事故数量时间序列表Table 1 Time series of the numbers of China’s hazardous chemicals leakage accidents in each month from 2010 to 2015

注：表中X1～X12分别对应2010年1月至12月；X13～X24分别对应2011年1月至12月；X25～X36分别对应2012年1月至12月；X37～X48分别对应2013年1月至12月；X49～X60分别对应2014年1月至12月；X61～X72分别对应2015年1月至12月。

1. 2 相空间重构

Takens相空间重构理论表明，只需考察一个分量就可以对系统相空间进行重构，在利用某些固定的延时点上的观测值找到m维向量后，就可以通过重构出的一个等价相空间把有规律的轨迹恢复出来。所以，相空间重构的核心就是选择适当的嵌入维数和延迟时间。

1999年，Kim等提出了C-C方法[16]，利用该方法能同时估算出延迟时间τ及嵌入维数m密切相关的嵌入窗宽τw=(m-1)τd。该方法具有独特的特点，它通过应用关联维积分，在减少互信息量法的计算量的同时也能保持时间序列的非线性特性，具有较强的抗噪声能力[17]。

设x(n)(n=1,2,…,N)为时间序列，Xi(n)={xi(n),xi(n+τ),…,xi[n+(m-1)τ]} (i=1,2,…,M)为相空间中的点,具体的C-C法描述如下：

嵌入时间序列的关联积分定义为下式的函数C:

式中:m为嵌入维数；N为时间序列的长度，也即时间序列中数据点的个数；r为领域半径的大小,r>0；τ为延迟时间(月)；θ为Heaviside的单位函数;Xi和Xj为相空间中的点。

关联维数D为

将时间序列x(n)(n=1,2,…,N)分成t个不相交的子时间序列，长度为INT(N/t)，INT取整,对于一般的自然数t，有

{x(1)，x(t+1)，x(2t+1)，…}

{x(2)，x(t+1)，x(2t+1)，…}

⋮

{x(t)，x(t+1)，x(2t+1)，…}

计算每个子时间序列的统计量S(m，N，r，τ)为

式中:Cl为第l个子时间序列的相关积分。

局部最大间隔可以取S(·)的零点或对所有的半径r相互差别最小的时间点。选择对应值最大和最小的两个半径分别为ri、rj，定义差量ΔS为

ΔS(m，t)=max[S(m，N，ri，t)]-min[S(m，N，rj，t)] (i≠j)

1. 3 基于最大Lyapunov指数的混沌特性判别

安全系统具有显著的混沌动力学特性，在理论上应该存在安全系统的混沌吸引子，1983年Grebogi证明了最大Lyapunov指数λmax>0，则系统一定存在混沌，所以可以在综合各种变量因素的基础上，寻找安全系统中正的Lyapunov指数，从而确定安全系统混沌吸引子的存在[19-20]。本文运用Lyapunov法来实现对危化品泄漏事故的混沌特性判别，具体算法如下：

(1) 根据上述C-C法求得的嵌入维数m和延迟时间τ，得到重构相空间:

X(t)={x(t),x(t-τ)，…，x[t-(m-1)τ]}

(2) 寻找中心点X(t)的临近状态X(tn)，并计算两点间的欧氏距离:

d=‖X(t)-X(tn)‖

(3) 计算x(t+1)，并利用最小二乘法做出回归直线的斜率，即为最大Lyapunov指数λmax，若λmax>0，则系统存在混沌。

2 危化品泄漏事故混沌时间序列模型的精度检验与预测

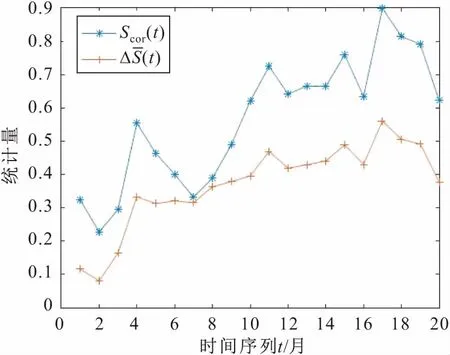
图2 延迟时间与嵌入窗宽的确定Fig.2 Determination of embedded window width and time delay

将所得到的重构的相空间代入上述Lyapunov算法中，计算得到最大Lyapunov指数λmax=0.666 2>0。所以，危化品泄漏事故的时间序列具有混沌特性，同时也表明在对危化品泄漏事故的时间序列进行相空间重构的基础上运用MATLAB软件进行仿真模拟是切实可行的[21]。

由此根据已统计的2010—2015年各月份我国发生的危化品泄漏事故的数量，利用建立的混沌时间序列模型，采用MATLAB软件对2016年各月份我国可能发生危化品泄漏事故的数量进行了预测，并与统计的原始数据进行了对比，其结果见图3。

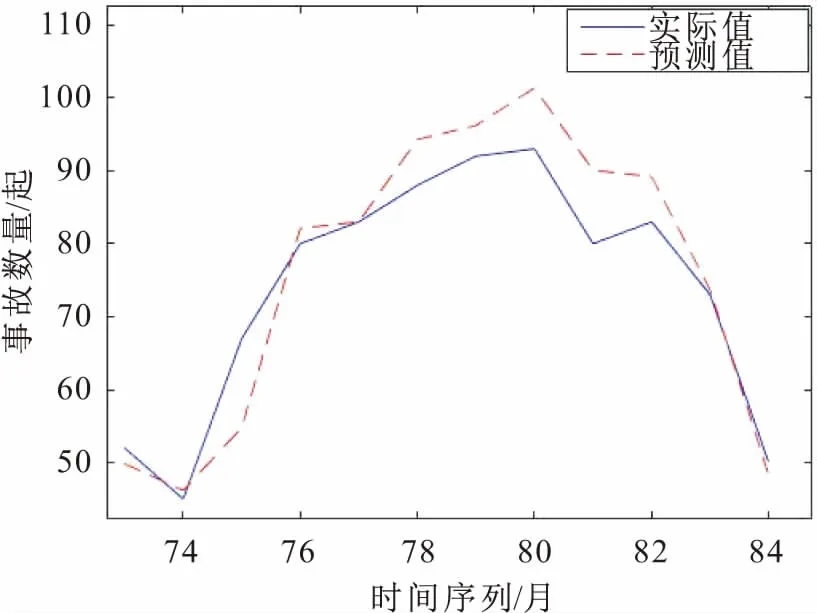
图3 2016年我国危化品泄漏事故数量的预测值与实际值的对比Fig.3 Comparison between simulated and real numbers of China's hazardous chemicals leakage accidents in 2016

由图3可见，2016年我国发生危化品泄漏事故数量的预测值与实际值的拟合趋势基本一致。

为了更好地体现建立的危化品泄漏事故混沌时间序列模型的预测值与实际值拟合程度的优劣，本文以2016年我国危化品泄漏事故数量为例计算了该模型的预测精度和拟合度指标，其结果见表2。

表2 危化品泄漏事故混沌时间序列模型的预测精度和拟合度指标Table 2 Prediction accuracy and goodness of fit of the chaotic time series model of hazardous chemicals leakage accidents

由表2可知：在2016年12个月的预测值中，三级预测精度以上的占83.33%，二级预测精度以上的占66.67%，各月份的拟合度指标均较高，模型在0.05的水平下显著；2016年全年预测值的预测精度达到二级标准，预测值与实际值的拟合度指标达到了97.52%，且误差能够满足预测要求，说明所建立的危化品泄漏事故混沌时间序列模型预测效果较好，具有较高的预测精度。

利用已建立的混沌时间序列模型，本文采用MATLAB软件对2017—2018年各月份我国可能发生危化品泄漏事故的数量进行了预测，其预测结果见表3。

表3 2017—2018年各月份我国发生危化品泄漏事故数量的预测值Table 3 Monthly Simulated number of China's hazardous chemicals leakage accidents in 2017 and 2018

由表3可知，我国2017年和2018年全年发生危化品泄漏事故的总数较2016年会有小幅度提升，但每年第二、三季度仍是危化品泄漏事故的高发期，该时间段仍是企业和政府部门须加强管制的重点时间段。从2010年至2018年的整体发展趋势来看，我国危化品泄漏事故的数量自2014年开始趋于稳定状态，总体在900起上下浮动。

尽管国家安监总局对危化品的监督管理提出了“两重点一重大”的安全监督办法，但未来两年我国危化品泄漏事故的数量仍有上升趋势。为究其原因，本文分析了相关部门发布的我国发生危化品泄漏事故的企业分布统计数据，结果发现中小型企业占八成以上，这些化工企业普遍存在从业人员整体素质偏低、企业安全管理不到位、工艺和设备落后等问题，导致危化品泄漏事故仍时有发生。为了降低危化品泄漏事故的发生率，减少人员伤亡和财产损失，并避免环境污染，我国政府部门应加强对相关企业尤其是涉及“两重点一重大”企业的安全监管，进一步提高从业人员的安全素质，不断完善作业条件，改革生产设备和工艺，全面加强和改进危化品的安全管理，积极配合监督管理部门的检查，进而有针对性地防范危化品泄漏事故的发生。

3 结论

(1) 危化品泄漏事故的发生虽然看似具有随机性和不确定性，但经过混沌特性判别发现其内部存在一定的规律，具有明显的混沌特性，属非线性混沌动力系统范畴，说明危化品泄漏事故系统整体具有可预测性，这为研究危化品泄漏事故的发生规律及其预防奠定了基础。

(2) 本文利用C-C法对时间序列进行相空间重构，利用最大Lyapunov指数进行混沌特性判别，从而建立了危化品泄漏事故的混沌时间序列模型，并利用建立的模型对2016年各月份我国发生的危化品泄漏事故的数量进行了预测，同时将预测值与实际值进行了对比验证，并用残差检验和拟合度指标进行了定量分析，证明了危化品泄漏事故的混沌时间序列模型的预测精度较高，具有较好的预测效果。

(3) 本文统计了2010—2016年我国发生的危化品泄漏事故的数量，利用建立的混沌时间序列模型对未来两年可能发生的危险化学品泄漏事故的数量进行了预测，并从事故发展趋势、事故原因及事故的预防措施等角度对事故统计数据进行了定性分析。结果表明：在未来两年中我国发生危化品泄漏事故的数量会有小幅度上升趋势，其原因与中小型化工企业数量在我国化工企业总数中占比较高有关，这为有关部门对化工企业的安全监管提供了重要依据，并为化工企业的安全生产管理工作和可持续发展策略提供了方向。

参考文献：

[1] 邵辉,施志荣,赵庆贤.混沌理论在事故分析及预测中的应用[J].中国安全科学学报,2005,15(4):21-24.

[2] 陈程,张兰芳,汪尚天.高速公路危化品事件处置持续时间预测模型[J].交通信息与安全,2017,35(1):55-61.

[3] 李建民,刁亚琳,宋绍珍,等.海上危化品运输系统安全突变评价[J].上海海事大学学报,2015,36(4):6-10.

[4] 文仁强,黄全义,黄东海.危化品泄漏扩散预测模型与GIS集成及其在应急决策中的应用研究[J].测绘通报,2008(4):52-54.

[5] 刘伟.危险化学品泄漏事故的混沌动力学特性分析[J].化工管理,2013(6):153-154.

[6] 高仁祥,周子康.预测困难与预测发展[J].中国管理科学,1996(4):58-64.

[7] 韩敏.混沌时间序列预测理论与方法[M].北京：中国水利水电出版社,2007.

[8] Farmer J D,Sidorowich J J.Predicting chaotic time series[J].PhysicalReviewLetters,1987,59(8):845-848.

[9] 孙义,黄显峰.基于最大Lyapunov指数的混沌预测在洪水实时预报中的应用[J].水利水电技术,2016,47(1):102-106.

[10]崔铁军,马云东.基于泛函网络的周期来压预测方法研究[J].计算机科学,2013,40(6A):243-246.

[11]张洋,马云东,崔铁军.基于小波和混沌优化LSSVM的周期来压预测[J].安全与环境学报,2014,14(4):63-66.