我国危险化学品事故灰色残差马尔科夫预测模型的建立及应用研究

杜晓燕,吴建华，朱庆明，张 浩

(安徽工业大学建筑工程学院，安徽 马鞍山 243032)

预测是以事物发生历史及现状为出发点，以调查资料和统计数据为依据，通过建立数学模型了解事物未来发展趋势及运行规律，为后续决策过程提供理论指导的一种方法。如今，预测决策理论和方法得到了广泛的应用，已发展成为理论分析、方法技术与实际应用相结合的专门学科。事故预测即是基于可知的事故信息和情报，对预测对象的安全状况进行的预报和测度，它可为相关部门制定事故预防措施、完善法律法规提供理论支撑。

随着国家对安全生产工作越来越重视，近年来有关专家学者基于不同预测指标，采用指数平滑、支持向量机、灰色预测、神经网络等方法对我国建筑事故[1-3]、危险化学品事故[4-5]、交通运输事故[6-7]等进行了预测研究。针对危险化学品(简称危化品)事故统计中样本数据信息不完备、波动大，没有完全可操作性的模型，本文在尽可能准确统计危化品事故的基础上，根据指标数据的特点，建立了适用于我国危化品事故预测的灰色残差马尔科夫预测模型。

1 预测模型

灰色预测模型适用于短中期的样本数据且信息量少的不确定灰色系统，而且预测精度较高，但当数据波动较大时将会影响其预测精度[8]。马尔科夫作为一种概率预测恰好适应于数据波动较大的预测。因此，在灰色预测的基础上，基于残差用马尔科夫进行优化预测，不仅可以克服数据波动性问题，还有助于提高预测精度[9]。本文以我国近年来危化品事故发生起数为指标，将灰色残差马尔科夫预测模型应用于我国危化品事故发生起数的预测中。

1. 1 灰色GM(1,1)模型

建立灰色GM(1，1)模型的步骤如下：

第一步：级比检验，进行建模可行性分析。

第二步：累加生成。

第三步：建立微分方程。

对生成数列x(1)建立白化形式的微分方程，称为一阶灰色微分方程，记为GM(1，1)：

(1)

式中:a、b为待定参数。

此微分方程满足初始条件：当t=t0时，x(1)=x(1)(t0)

求解微分方程，连续微分方程的解为：

(2)

则对等间隔取样的离散值(其中t0=1)，即可得灰色GM(1，1)预测模型：

(3)

按最小二乘法，求得微分方程的系数向量：

(4)

式中：

Y=(x(0)(2),x(0)(3),…,x(0)(n))T

(5)

(6)

1. 2 马尔科夫优化预测

马尔科夫模型可表示为

x(n)=x(t)·Pn-1

(7)

式中:x(n)为n时刻的状态概率向量;x(t)为初始时刻t的状态概率向量；P为状态转移概率矩阵。

上式具有根据P及x(t)预测第(n-1)步状态的意义。该模型的关键在于如何获得状态转移概率矩阵P。

设在某一事件的发展过程中有n个可能的状态，即E1,E2,…,En,事件从某一状态Ei出发，下一时刻转移到其他状态Ej的可能性称为状态转移概率pij，则状态转移概率矩阵P为

(8)

通常情况下采用频率近似等于概率的原理计算状态转移概率，即

pij=Mij/Mi

(9)

式中：Mi为状态Ei出现的总次数;Mij为状态Ei到状态Ej的次数。

设n时刻预测值为x(0)(n)，状态转移概率向量为x(n),往往以最大概率所处状态作为未来的发展状态，那么最大概率状态区间的中间值将作为n时刻的预测值。

2 我国危险化学品事故预测模型的建立

2. 1 原始指标数据

本文以我国历年发生的危化品事故起数为指标，依据中国化学品安全协会(http://www.chemicalsafety.org.cn/index.php)公布的2006—2015年我国危化品事故信息，整理出2006—2015年我国历年发生的危化品事故起数，见表1。

表1 2006—2015年我国历年发生的危化品事故起数Table 1 Number of hazardous chemical accidents from 2006 to 2015 in China

由表1可见，2006—2011年我国发生的危化品事故起数略呈线性降低趋势，2013—2015年呈线性递增趋势，这两个时间段内均呈单调变化，说明灰色预测有适用性；但不可忽视的是2012年前后数据有一个突然波动，可能会给灰色预测带来较大的误差。

2.2 灰色GM(1,1)预测模型的建立

本文首先以2006—2014年我国发生的危化品事故起数为原始样本建立灰色GM(1，1)预测模型，并以2015年实际发生的事故起数为验证样本来验证所建立的灰色GM(1，1)预测模型的可靠性。根据前述方法，所建立的我国危化品事故灰色GM(1,1)预测模型为

(10)

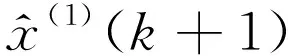
(11)

由此计算得到灰色GM(1,1)模型的2015年预测值为152起，与实际值比较，其相对误差为29.9%。根据模型精度检验标准，当相对误差超过20%时，为不合格[10]。因此上述所建立的灰色GM(1,1)模型预测误差过大，不适合于预测我国危化品事故的发展趋势。为了提高模型的预测精度，以其灰色残差为基础，进一步用马尔科夫进行优化预测。

2. 3 基于灰色残差的马尔科夫优化预测

2.3.1 计算灰色残差

根据上述建立的灰色GM(1,1)预测模型，可计算得到2006—2014年我国历年发生的危化品事故起数的灰色残差[11]，其计算结果见表2。

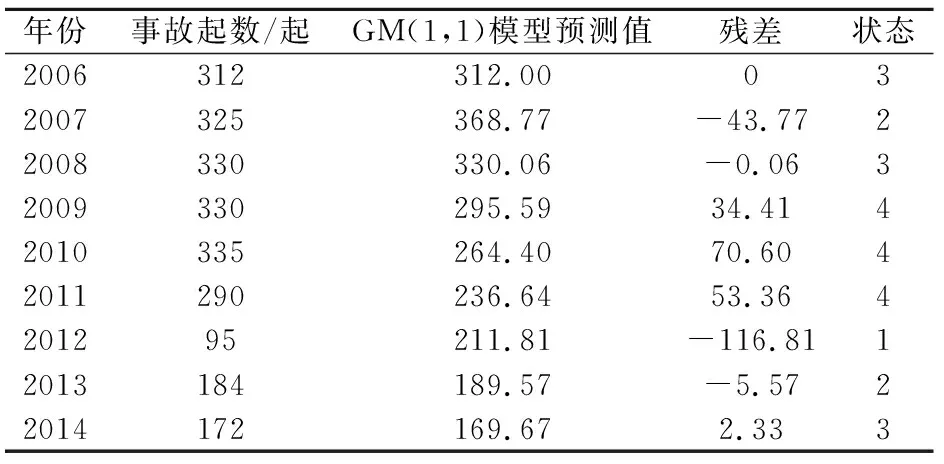
表2 2006―2014年我国历年发生的危化品事故起数的灰色残差计算结果Table 2 Gray residue calculation results of hazardous chemical accidents from 2006 to 2014 in China

2.3.2 基于灰色残差的马尔科夫状态划分

采用马尔科夫有序样本法对我国危化品事故起数序列进行状态划分，根据表2，可将计算得到的灰色残差划分为以下4个状态：

(-∞,-69.95],(-69.95,-23.1],(-23.1,23.75],(23.75,+∞)

为了计算区间的中点，取残差的最小值为下限，残差的最大值为上限，将上述区间定义为有限区间，即将残差划分为

[-116.81,-69.95],(-69.95,-23.1],(-23.1,23.75],(23.75,70.6]

得到状态划分空间为

其中：Q1i表示状态i的最小值：Q2i表示状态i的最大值。

据此可以确定各年度的状态。

2.3.3 构造状态转移概率矩阵

根据马尔科夫预测理论，分别构造一步、两步、三步、四步状态转移概率矩阵如下：

2.3.4 根据状态转移概率矩阵确定预测值

本文选取离2015年最近的2011—2014年4个时间段，分别计算出状态转移4步的概率结果并进行加权叠加，用来确定预测值，其结果见表3。

表3 状态转移概率计算结果Table 3 State transition probability calculation results

权重是考虑了各步长样本的自相关系数而求得的。采用择优加权马尔科夫预测法，得到2015年我国危化品事故起数的残差处于状态1的概率为

0.099×0.151 6=0.015

处于状态2的概率为

0.315×0.151 6+0.5×0.033 3+0.5×0.268 5+0.5×0.546 6=0.471 9

处于状态3的概率为

0.222×0.151 6=0.034

处于状态4的概率为

0.364×0.151 6+0.5×0.033 3+0.5×0.268 5+0.5×0.546 6=0.479 4

通过比较状态1、2、3、4的概率值，预测2015年我国危化品事故起数的灰色残差将处于状态4。

2.3.5 模型验证

根据灰色残差马尔科夫预测模型，2015年我国危化品事故起数的预测值为

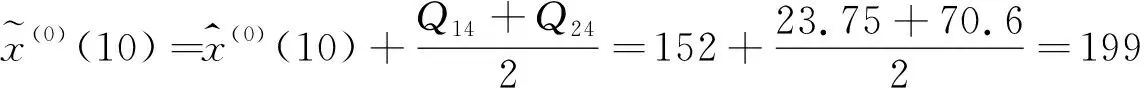
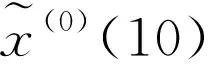
其相对误差为

经检验，灰色残差马尔科夫预测模型的预测精度合格[10]，其与灰色GM(1，1)预测模型的精度对比见表4。

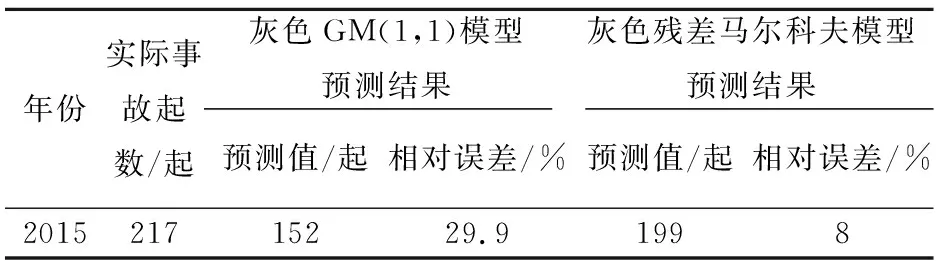
表4 灰色GM(1，1)预测模型与灰色残差马尔科夫预测 模型的精度比较Table 4 Accuracy comparison between GM(1,1) and the gray residual Markov prediction model

由表4可见，采用灰色残差马尔科夫模型预测的相对误差值比单纯使用灰色GM(1，1)模型的相对误差值小很多，说明其预测精度较高。可见，对于原始数据波动性较大的样本，采用灰色残差马尔科夫模型进行预测更加准确。

3 我国未来年份发生危化品事故起数的预测

综上分析可知，基于灰色残差马尔科夫预测模型能更精确地预测我国危化品事故的发生情况，因此可采用该模型对我国未来年份发生危化品事故的起数进行预测，以了解未来我国危化品事故的发展趋势，为危化品事故防控工作提供理论指导。本文以2006—2015年我国已发生的危化品实际事故起数数据为原始样本，通过建立灰色GM(1，1)预测模型、计算灰色残差、马尔科夫优化预测三大步骤来预测未来年份我国发生危化品事故的起数。限于篇幅，具体步骤省略，得到的最终结果如下：

(1) 基于2006—2015年原始数据建立的灰色GM(1,1)预测模型如下：

(2) 计算灰色残差：根据上述建立的灰色GM(1，1)预测模型，可计算得到2006—2015年我国历年发生的危化品事故起数的灰色残差，其计算结果见表5。

(3) 马尔科夫优化预测： 根据表5，将计算得到的灰色残差划分为以下4个状态：

[-128.60,-80.23],(-80.23,-31.85],(-31.85,16.50],(16.50,64.90]

(12)

经计算，预测2016年我国危化品事故起数的灰色残差将处于状态4，因此预测得到2016年我国危化品事故起数将为193起。

表5 2006—2015年我国历年发生的危化品事故起数的灰色残差的计算结果Table 5 The gray residue calculation results of hazardous chemical accidents from 2006 to 2015

4 结 论

随着工业发展和社会进步，人们对化工产品的依赖性越来越强，危化品事故层出不穷。本文根据近年来我国危化品事故发生的特点，建立了灰色残差马尔科夫预测模型，对未来我国发生的危化品事故起数进行了预测，并通过实例对该模型的精度进行了验证，结果证明灰色残差马尔科夫预测模型能更准确地反映当前我国危化品事故的发展趋势，可为事故的防控提供理论依据。

参考文献：

[1] 李书全，窦艳杰.基于RS-SVM模型的建筑安全事故预测模型[J].统计与决策,2008(19):56-58.

[2] 严小丽，何超，黄怡浪.三次指数平滑法在建筑事故预测中的应用[J].统计与决策,2015(10):72-73.

[3] 殷乃芳，孙磊.基于灰色-马尔柯夫模型的建筑安全事故死亡人数预测[J].工程管理学报,2010(6):652-655.

[4] 张悦，李峰，石超，等.改进GM(1,1)模型在我国危险化学品事故预测中的应用[J].中国安全生产科学技术,2012,8(5):91-95.

[5] 匡蕾，王斌.基于改进FNN的危险化学品运输事故智能预测[J].中国安全科学学报,2012,22(9):97-102.

[6] 李军怀，高瞻，王志晓，等.基于指数平滑和马尔可夫链的短时交通流量预测[J].计算机系统应用,2013,22(12):132-135.

[7] 赵玲，许宏科，程鸿亮.基于最优加权组合模型的道路交通事故预测[J].计算机工程与应用,2013,49(24):11-15.

[8] 马杰，宋建池.基于GM(1,1)模型预测我国未来化工企业安全生产形势[J].安全与环境工程,2009,16(5):89-92.

[9] 陈勤.基于马尔科夫灰色残差GM(1,1)模型的火灾损失预测[J].工业安全与环保,2015(1):70-72.

[10]刘花璐，汤涛.湖北省GDP预测的数学模型及其影响因素分析[J].数学的实践与认识,2015,45(5):262-269.

[11]杜晓燕，程五一，刘斌，等.安徽省道路交通事故影响因素分析及其预测研究[J].数学的实践与认识,2016,46(1):70-76.