考虑层间应力的厚复合材料结构多级优化设计方法
2018-05-31曹华王志瑾原潇韩宇候天骄
曹华,王志瑾,原潇,韩宇,候天骄
(南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
0 引 言
随着复合材料结构在各领域的大量使用,逐渐由次承力结构渗透到大型主承力结构。在国外一些军用、民用飞机和卫星的纤维复合材料应用中出现了大量的厚复合材料结构,例如卫星的桁架、飞机平尾的枢轴及太阳翼连接架等结构。与复合材料薄壁结构相比,厚复合材料结构的层间应力问题更加突出,在优化设计时必须考虑层间破坏[1]。许多学者对厚复合材料结构的层间应力分析进行了研究,并取得了显著成果。R.Byron Pipes等[2]应用弹性力学理论推导了有限宽度复合材料层合板在均匀轴向拉力作用下的微分方程,并通过有限差分法求得了层间应力;张培新等[3]建立了复合材料层合板的准三维有限元模型,分析了受面内载荷的层压复合材料的层间应力;王秋宇等[4]应用近似方法分析了梁圆角区的层间应力。总结上述层间应力的分析方法,能够发现这些方法都具有一定的局限性,只适用于简单载荷边界条件,或者只适用于简单的复合材料平板结构,不具有通用性。有限元方法因其通用性被广泛应用,商业有限元软件Abaqus具有强大的复合材料分析能力被广泛应用于分析厚复合材料结构的三维应力。
为了使复合材料结构在满足安全性要求的同时,复合材料的各组分材料性能够得到最有效利用,从而最大限度的发挥复合材料的性能优势,减轻结构重量,必须进行结构优化设计。Jin Peng等[5]考虑强度约束、刚度约束、屈曲约束以及铺层工艺性约束,采用遗传算法对大型复合材料机翼盒段的蒙皮厚度及铺层顺序进行了优化,使结构重量减轻了36.6%;Liu Jian等[6]基于径向基神经网络代理模型,应用遗传算法对复合材料卫星结构进行了尺寸优化;茅佳兵等[7]对机翼加筋板结构进行了优化设计,从而提高了结构的承载效率;史旭东等[8]采用遗传算法对大展弦比复合材料机翼结构进行了优化设计。上述复合材料结构优化设计的研究都是针对薄壁结构的,而针对厚复合材料结构的优化设计的研究几乎空白。与复合材料薄壁结构相比,厚复合材料结构的优化设计存在众多的难点。例如厚复合材料结构的力学分析存在难点、厚复合材料结构的优化需要考虑层间强度,而层间应力的计算存在较大的困难;厚复合材料结构的优化设计变量多,有些设计变量是离散的、不等式约束多、性能约束是设计变量的隐函数等。
工程实际应用的厚复合材料结构,为了避免由于固化应力而引起的翘曲,通常采用很多铺层相同的子层板叠成[9]。本文针对具有周期性铺层方式的厚复合材料层合板结构的铺层优化设计,提出一种厚复合材料层合板结构子层数、子层内层数、子层内铺层比例及铺层顺序的多级优化设计方法。结合算例,通过Matlab编写遗传算法,并应用Isight集成Matlab来实现该优化设计方法。
1 优化问题描述
工程实际应用的厚复合材料结构通常采用很多铺层相同的子层板叠成,这种厚复合材料结构的铺层设计参数有子层数、子层内层数、子层内铺层比例及铺层顺序。厚复合材料结构在承受较大的横向载荷时,除了产生弯曲应力外,还将产生较大的剪切应力,由此引起层间剪切应力。然而复合材料的层间强度通常很低,引起的层间剪切应力可能造成层间破坏,所以在厚复合材料结构的优化设计中,除了需考虑面内强度,还需考虑层间剪切强度。
厚复合材料结构的优化设计中设计变量为子层数、子层内层数、子层内铺层比例及铺层顺序。优化问题为寻找合适的设计变量,在满足强度要求的条件下使结构重量最轻。数学模型为
Find:X=(x1,x2,X3,X4)T
Min:m=f(x1,x2,X3,X4)
Subject to:g1(x1,x2,X3,X4)≤1
g2(x1,x2,X3,X4)≤1
(1)
式中:x1,x2为厚复合材料结构的子层数、子层内层数;X3为子层内铺层比例,X3=(N0,N45),其中N0、N45分别为子层内0°及45°铺层层数,因为均衡铺层,故-45°的铺层层数N-45=N45,90°铺层层数N90=x2-N0-2N45;X4为铺层顺序;m为目标函数结构质量;g1为面内强度约束;g2为层间强度约束。
本文采用商业有限元软件Abaqus分析厚复合材料结构的三维应力,面内失效准则采用Tsai-Hill准则,如式(2)所示,层间失效准则如式(3)所示。
(2)
(3)
式中:X、Y和S为单层X复合材料纵向强度、横向强度及剪切强度;Z为层间法向强度;Sxz与Syz为层间剪切强度。
厚复合材料层合板结构还需满足一些其他工艺性要求,优化后的铺层应当满足以下铺层设计要求[10]:①采用0°、±45°、90°的标准铺层角;②子层板进行对称均衡铺层设计;③在子层板中,0°、±45°、90°四种铺层角的任意角度应有大于等于10%的纤维;④在子层板中,0°、±45°、90°四种铺层角的任意角度应有小于等于60%的纤维。
2 多级优化方法及流程
对于由铺层相同的子层板叠成的厚复合材料结构的优化设计问题,主要的设计变量包括子层数、子层内层数、子层内铺层比例及铺层顺序。这些设计变量都是离散变量,它们之间相互影响,且对结构质量的影响不同。本文提出一种多级优化设计方法,将厚复合材料结构的复杂优化问题分解为两级优化。第一级优化是基于代理模型的优化,其目标函数为结构质量最轻,设计变量为子层内层数及铺层比例。第二级优化分为两个层次进行,系统层的设计变量为子层数,考虑面内强度及层间强度约束;子系统层采用遗传算法优化铺层顺序。总优化流程如图1所示。
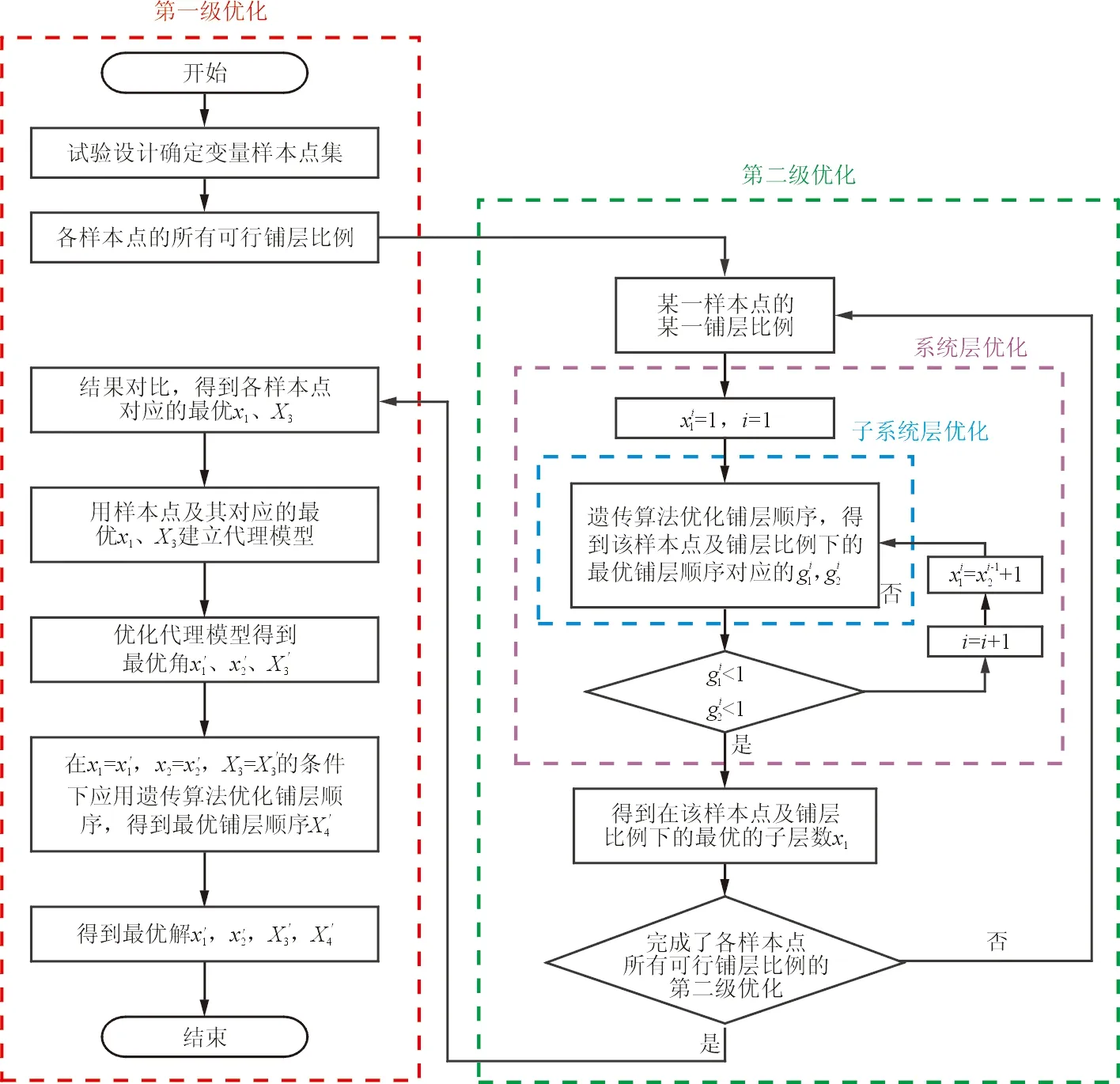
图1 优化流程图
2.1 第一级优化设计
本级优化的设计变量为子层内层数与铺层比例,目标函数为结构质量。通过试验设计方法确定子层内层数的样本点集,根据铺层设计工艺性要求得到每个样本点所有可行的铺层比例。针对某个样本点的某一可行铺层比例,采用第二级优化可以得到在该子层内层数及铺层比例下的最优子层数。每个样本点的所有可行的铺层比例都采用第二级优化进行子层数的优化,并进行结果对比,得到各样本点对应的最优铺层比例及子层数。利用样本点及其对应的最优铺层比例与子层数建立代理模型,对代理模型进行优化得到最优解。
首先确定设计变量x2的取值范围,采用试验设计方法在x2的设计空间中确定样本点集。针对每个样本点,根据铺层设计要求的第(2)条、第(3)条及第(4)条确定各个样本点可行的铺层比例。以样本点x2=16为例,满足铺层设计要求的铺层比例如表1所示。

表1 可行铺层比例(x2=16)
以x2=16为例,应用第二级优化方法对x2为16时的所有可行铺层比例进行优化,即对表1的7种可行铺层比例分别进行第二级优化。每种铺层比例可以优化得到对应的最优子层数及铺层顺序。对比7种可行铺层比例对应的最优子层数 。将7种可行铺层比例对应的最优子层数中最小的x1及其对应的铺层比例X3作为x2=16对应的最优子层数及铺层比例。若7种可行铺层比例对应的最优子层数中存在多个最小的x1,则进一步对比层间应力因子g2,将最小g2对应的子层数x1及铺层比例X3作为x2=16对应的最优子层数及铺层比例。
通过第二级优化和结果对比可以得到每个样本点对应的最优铺层比例及子层数,利用这些样本点的值及对应最优铺层比例及子层数建立第一级优化系统的代理模型。该代理模型是一个三层径向基神经网络,输入层的节点个数为1,输出层节点个数为3;输入变量为x2/2,输出变量为x1及X3/2=(N0/2,N45/2),如图2所示。将所有样本点的优化结果作为训练实例,对径向基神经网络进行训练,从而得到径向基神经网络代理模型。
Find:X=(x2,X3)T
Min:m=f(x2,X2)
(4)
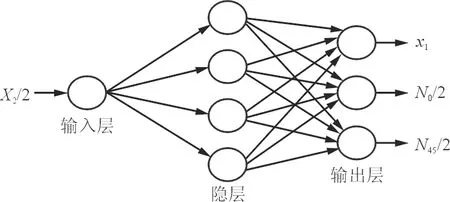
图2 径向基神经网络模型

图3 第一级优化设计流程
2.2 第二级优化设计
第二级优化系统是在给定子层内层数及铺层比例下优化子层数及铺层顺序。本级优化分为系统层与子系统层两个层次进行,优化流程如图4所示。系统层的设计变量为子层数,目标函数为质量最小,约束为层间强度及面内强度满足要求。系统层的约束函数值g1与g2由子系统层优化求解得到。因为目标函数结构质量与子层数成正比,系统层优化问题可描述为寻找一个最小的子层数使得结构满足层间强度及面内强度要求。数学模型如下:
Find:x1
Min:m=f(x1)
Subject to:g1(x1)≤1
g2(x1)≤1
(5)
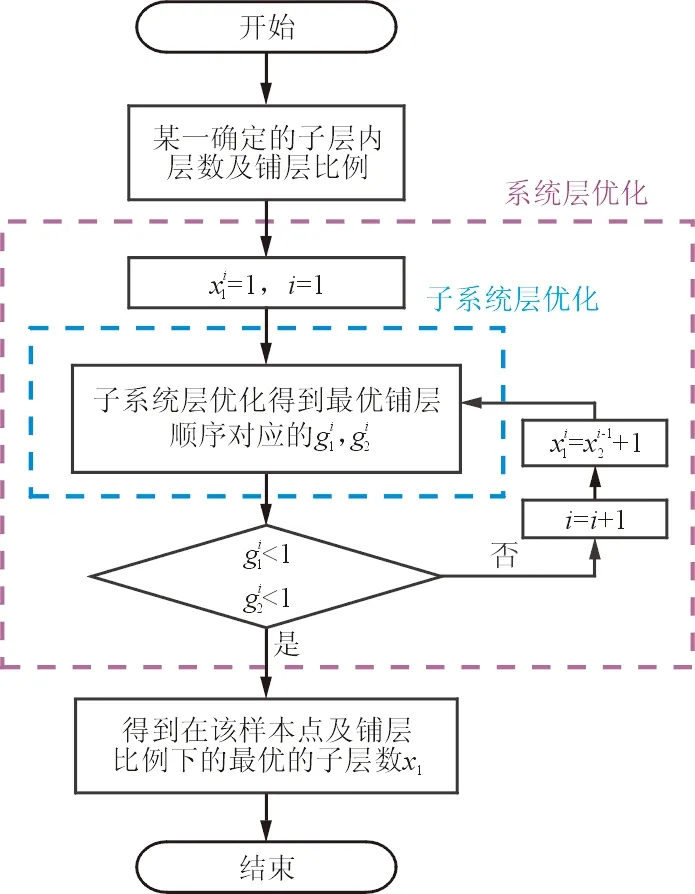
图4 第二级优化设计流程图
子系统层是在给定子层内层数0°、±45°、90°的层数、子层数的情况下进行铺层顺序优化。子系统层采用遗传优化算法,设计变量为铺层顺序,目标函数为层间应力最小,约束为面内应力满足强度要求,数学模型如下:
Find:X4
Min:g=g2(X4)
Subject to:g1(X4)≤1
(6)
本文遗传算法采用文献[11]中的编码方法,即数字编码串的方法,要求每个个体的染色体编码中不允许有重复的基因码。选取一种初始铺层顺序,此铺层编码对应的角度则是确定的,优化后的铺层经译码后可得到相应的角度[11-12]。
第二级优化系统的流程图如图4所示,系统层设计变量x1的初始值为其设计空间最小值1,往大的方向寻优,x1的优化步长为1。对于每个系统层设计变量x1,将子系统层优化得到的最优铺层顺序对应层间应力因子及面内应力因子作为系统层优化的约束函数值。若最优铺层顺序对应层间应力因子及面内应力因子满足系统层约束条件,则该子层数为最优子层数,优化结束,否则子层数加1,再进入子系统层优化,直到某一子层数下的最优铺层顺序对应层间应力因子及面内应力因子满足系统层约束条件。
3 算 例
3.1 算例1
由铺层相同的子层板叠成的复合材料圆管的外径D=120 mm,长L=500 mm。一端固支,另一端受横向载荷F=100 kN,如图5所示。铺层材料为ZT7H/5429,材料性能如表2所示,强度参数如表3所示,单层厚度为0.125 mm。该复合材料圆管由多个铺层相同的子层板堆叠而成,需要通过优化确定的参数有:子层数、子层内层数、子层内铺层比例及铺层顺序。

图5 复合材料圆管模型
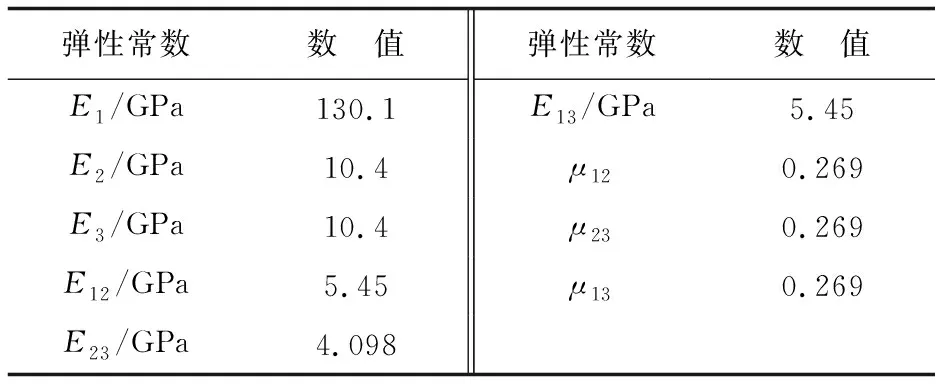
弹性常数数 值弹性常数数 值E1/GPa130.1E13/GPa5.45E2/GPa10.4μ120.269E3/GPa10.4μ230.269E12/GPa5.45μ130.269E23/GPa4.098

表3 ZT7H/5429强度参数
子层采用对称铺层,子层内层数x2的取值范围为10~30的偶数,采用试验设计方法确定x2的样本点集为{10,16,20,22,26,30},并根据铺层工艺要求列出所有可行的铺层比例。对各个样本点应用Abaqus二次开发语言Python实现参数化建模,用Matlab语言编写遗传算法,根据图4所示的优化流程,应用Isight集成Matlab实现该优化方法。
以x2=16为例,子层内层数x2=16对应的所有可行铺层比例如表1所示,分别对这些铺层比例进行第二级优化,优化结果如表4所示。

表4 各可行铺层比例对应的最优解(x2=16)
从表4可以看出:子层内铺层比例对总层数(质量)的影响很大,当子层内铺层比例为N0=2,N45=N-45=6,N90=2时,子层数达到29,总层数为464,而子层内铺层比例为N0=8,N45=N-45=2,N90=4时,子层数为4,总层数为64;对比表4中子层数,得到x2=16对应的最优铺层比例X3=(8,2),最优子层数x1=4。
子层内层数x2=16,子层内0°、±45°、90°铺层比例为6∶4∶2时的子层数的优化结果曲线如图6所示。
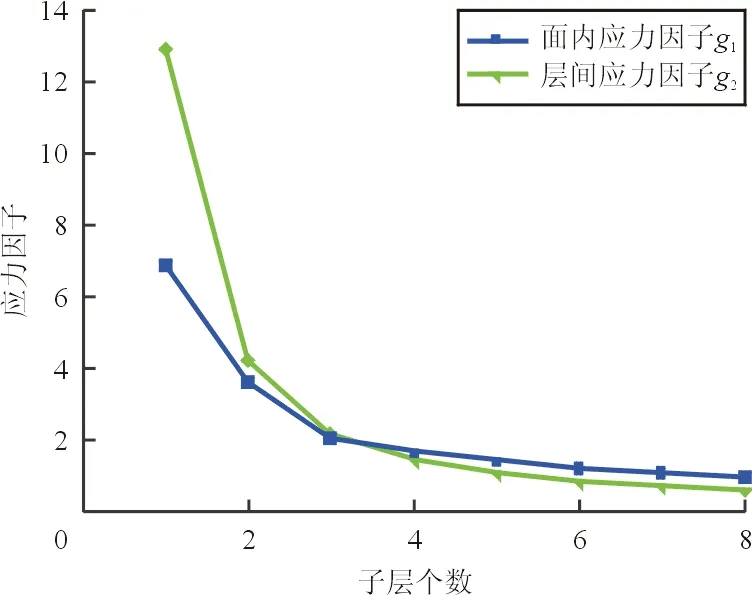
图6 第二级系统层优化过程
从图6可以看出:g1和g2都随着子层数的增加而减小,且随着子层数的增加g1和g2的斜率减小;子层数较大时g2>g1,层间应力因子g2起临界约束作用,表明厚复合材料层合板结构的层间破坏比面内破坏先发生,在厚复合材料结构的设计中必须考虑层间强度。
子层内层数x2=30,子层内0°、±45°、90°铺层比例为10∶6∶8,子层数x1=3时的铺层顺序优化结果曲线如图7所示。

图7 最优层间应力因子进化过程
从图7可以看出:遗传优化算法是收敛的,通过遗传优化能够高效的寻找到最优的铺层顺序,从而改进层间应力因子。
分别对各样本点的所有可行铺层比例进行优化并对比结果,得到各个样本点对应的对应最优铺层比例及子层数,如表5所示。

表5 各样本点对应的最优解
利用样本点及其对应的最优铺层比例与子层数建立径向基神经网络代理模型,在建立代理模型时,以设计变量x2的所有样本点及其对应最优铺层比例及子层数为训练实例,即用表5中的数据进行训练。该代理模型是一个三层径向基神经网络,输入层的节点个数为1,输入变量为x2/2,输出节点个数为3,输出变量分别为x1、N0/2及N45/2。用训练后的代理模型计算所有x2/2值的x1、N0/2及N45/2,并将径向基代理模型输出结果进行四舍五入得到实际结果,如表6所示。

表6 RBF输出和实际输出结果
从表6可以看出:x2=20,N0=12,N45=2,x1=3时,总层数最少,厚复合材料圆管结构质量最小。
对x2=20,N0=12,N45=2,x1=3时进行铺层顺序优化,得出最优铺层顺序为[0/0/-45/0/45/0/0/90/0/90]s。确定该复合材料圆管最优尺寸及铺层为:壁厚7.5 mm,内径为105 mm,子层数为3,子层铺层方式为[0/0/-45/0/45/0/0/90/0/90]s。
3.2 算例2
由铺层相同的子层板叠成的厚复合材料矩形板的尺寸如图8所示,受三点弯曲,横向载荷为q。该厚复合材料矩形板的单层板厚度及力学性能同算例1。该板的初始厚度H=15 mm,子层数为6,各子层板的铺层方式为[0/0/45/-45/0/45/-45/0/90/0]s,载荷q=667 N/mm。该板使用式(2)和式(3)的强度准则,面内应力因子g1=0.35,层间应力因子g2=1.00,刚好发生层间破坏。为了减轻结构重量,对该板的进行优化,设计变量包括:子层数、子层内层数、子层内铺层比例及铺层顺序。
子层采用对称铺层,子层内层数x2的取值范围为10~30的偶数,采用试验设计方法,确定x2的样本点集为{10,16,18,22,26,30},并根据铺层工艺要求列出所有可行的铺层比例。
以x2=16为例,子层内层数x2=16对应的所有可行铺层比例如表1,分别对这些铺层比例进行第二级优化,优化结果如表7所示。
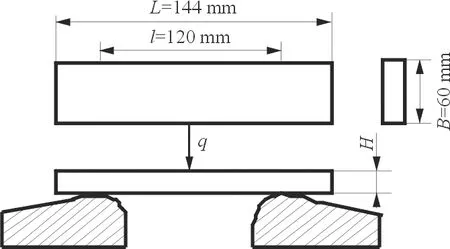
图8 三点弯曲

N0N45子层数最优铺层顺序g1g2总层数249[90/-45/90/-45/45/45/90/0]s0.6040.8191442610[-45/90/-45/45/-45/45/45/0]s0.4680.821160428[90/90/-45/90/90/45/0/0]s0.5580.809128449[90/-45/-45/90/45/45/0/0]s0.3380.734144628[0/0/90/0/90/90/-45/45]s0.2830.753128648[0/0/0/90/-45/45/45/-45]s0.3230.969128827[0/0/90/0/0/-45/90/45]s0.3260.950112
从表7可以看出:子层内铺层比例对总层数(质量)的影响很大,当子层内铺层比例为N0=2,N45=N-45=6,N90=2时,子层数达到10,总层数为160,而子层内铺层比例为N0=8,N45=N-45=2,N90=4时,子层数为7,总层数为112。对比表7中子层数,得到x2=16对应的最优铺层比例X3=(8,2),最优子层数x1=7。
子层内层数x2=16,子层内0°、±45°、90°铺层比例为6∶4∶2时的子层数的优化结果曲线如图9所示。

图9 第二级系统层优化过程
从图9可以看出:g1和g2都随着子层数的增加而减小,且随着子层数的增加g1和g2的斜率减小;层间应力因子起临界约束作用,表明厚复合材料层合板结构的层间破坏比面内破坏先发生,在厚复合材料结构的设计中必须考虑层间强度。
子层内层数x2=28,子层内0°、±45°和90°铺层比例为16∶4∶4,子层数x1=4时的铺层顺序优化结果曲线如图10所示。
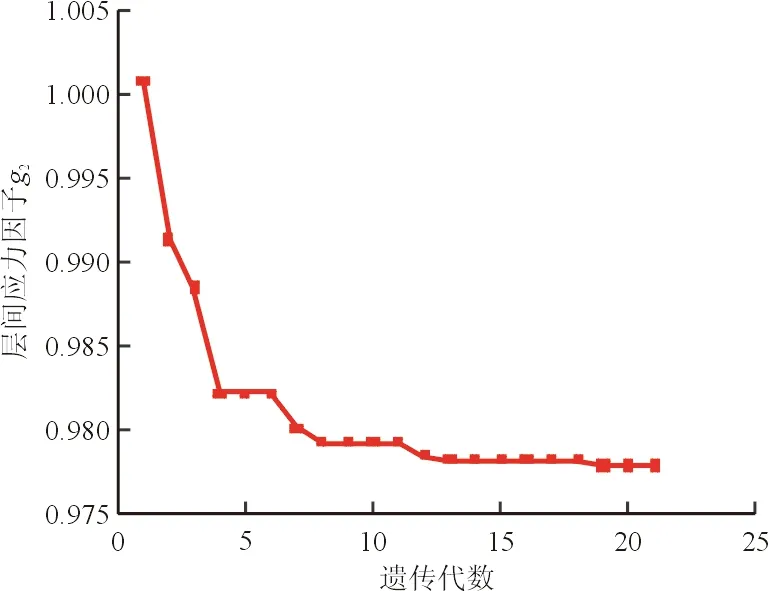
图10 最优层间应力因子进化过程
从图10可以看出:遗传优化算法是收敛的,通过遗传优化能够高效的寻找到最优的铺层顺序,从而改进层间应力因子。
分别对各样本点的所有可行铺层比例进行优化并对比结果,得出各个样本点对应的对应最优铺层比例及子层数,如表8所示。

表8 各样本点对应的最优铺层比例及子层数
同理,利用样本点及其对应的最优铺层比例与子层数建立径向基神经网络代理模型。使用训练后的代理模型计算所有x2/2值的x1、N0/2及N45/2,并将径向基代理模型输出结果进行四舍五入得出实际结果,如表9所示。
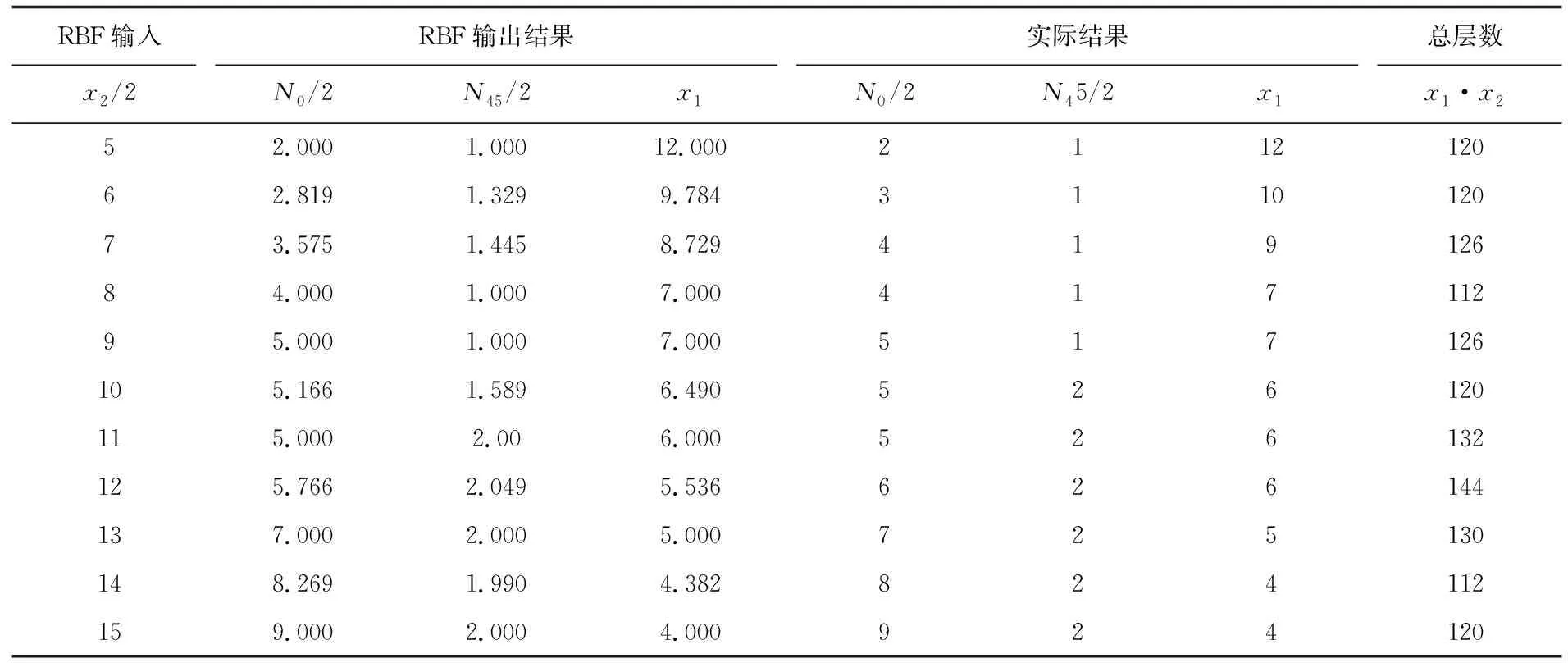
表9 RBF输出和实际输出结果
从表9可以看出:当x2=16,N0=8,N45=2,x1=7(第一组)和x2=28,N0=16,N45=4,x1=4(第二组)时,总层数同时达到最小值112,该板质量最小。
再对这两组厚板进行铺层顺序优化,得出:第一组的最优铺层顺序为[0/0/90/0/0/-45/90/45]s,对应的g1=0.326,g2=0.950;第二组的最优铺层顺序为[45/0/0/0/0/45/0/0/90/0/-45/0/90/-45]s,对应的g1=0.395,g2=0.986,可以看出第一组的g2小于第二组的g2,故该板的最优解为x2=16,N0=8,N45=2,x1=7(第一组),铺层顺序为[0/0/90/0/0/-45/90/45]s。与初始设计的子层铺层方式[0/0/45/-45/0/45/-45/0/90/0]s,子层数为6相比,结构质量减小6.67%,表明该优化算法是有效的。
4 结 论
(1) 本文针对具有周期性铺层方式的厚复合材料层合板结构的子层数、子层内层数、子层内铺层比例及铺层顺序的优化设计提出了一种多级优化设计方法。在优化设计过程中,考虑了面内强度及层间强度约束,使优化后的厚复合材料结构在设计载荷作用下不发生层间破坏。多级优化设计方法将厚复合材料层合板的复杂优化问题分解为多个层次进行优化,从而将具有不同量纲、对结构影响程度不同的设计变量分离,实现了厚复合材料结构的优化设计。
(2) 通过算例表明了本文提出的优化方法的有效性,能够很好地实现具有周期性铺层方式的厚复合材料层合板结构的优化设计。该优化方法为厚复合材料结构的初始设计提供了思路,具有重要的工程实用价值。
[1] 陈烈民, 杨宝宁. 复合材料的力学分析[M]. 北京: 中国科学技术出版社, 2006: 147-152.
Chen Liemin, Yang Baoning. Mechanical analysis for composite materials[M]. Beijing: Science and technology of China Press, 2006: 147-152.(in Chinese)
[2] R Byron Pipes, Pagano N J. Interlaminar stresses in composite laminates under uniform axial extension[J]. Journal of Composite Materials, 1970, 34(4): 538-548.
[3] 张培新, 李亚智. 受面内载荷的层压复合材料的层间应力分析[J]. 机械强度, 2006, 28(2) : 224-228.
Zhang Peixin, Li Yazhi. Interlaminar stress analysis of composite laminates subjected to in-plane loading[J]. Journal of Mechanical Strength, 2006, 28(2): 224-228.(in Chinese)
[4] 王秋宇, 陈普会, 王爱军. 复合材料梁圆角区层间应力计算分析方法[J]. 江苏航空, 2014 (1): 18-20.
Wang Qiuyu, Chen Puhui, Wang Aijun. Calculation and analysis method of interlaminar stress in the fillet area of composite beam[J]. Jiangsu Aviation, 2014 (1): 18-20.(in Chinese)
[5] Peng Jin, Bifeng Song, Xiaoping Zhong. Structure optimization of large composite wing box with parallel genetic algorithm[J]. Journal of Aircraft, 2012, 48(6): 2145-2148.
[6] Liu Jian, Teng Long, Renhe Shi, et al. Composite structure optimization for satellite using discrete dynamic radial basis function metamodel[C]. 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2016.
[7] 茅佳兵, 王生楠, 刘俭辉. 机翼复合材料加筋壁板结构的优化设计[J]. 航空工程进展, 2014, 5(3): 390-396.
Mao Jiabing, Wang Shengnan, Liu Jianhui. Optimization design for stiffened composite wing panel[J]. Advances in Aeronautical Science and Engineering, 2014, 5(3): 390-396.(in Chinese)
[8] 史旭东, 陈亮, 张碧辉, 等. 基于遗传算法的大展弦比复合材料机翼结构优化设计[J]. 航空工程进展, 2015, 6(1): 110-115.
Shi Xudong, Chen Liang, Zhang Bihui, et al. Structural optimization design of high aspect ratio composite wing based on genetic algorithm[J]. Advances in Aeronautical Science and Engineering, 2015, 6(1): 110-115.(in Chinese)
[9] 罗祖道, 李思简. 各向异性材料力学[M]. 上海: 上海交通大学出版社, 1994: 355-362.
Luo Zudao, Li Sijian. Anisotropic material mechanics[M]. Shanghai: Shanghai Jiaotong University Press, 1994: 355-362.(in Chinese)
[10] Kassapoglou C. Design and analysis of composite structures with applications to aerospace structures[M]. 2nd ed. Chichester: John Wiley & Sons Ltd, 2013: 343-345.
[11] 修英姝, 崔德刚. 复合材料层合板稳定性的铺层优化设计[J]. 工程力学, 2005, 22(6): 212-216.
Xiu Yingshu, Cui Degang. Ply optimization design for stability of composite laminates[J]. Engineering Mechanics, 2005, 22(6): 212-216.(in Chinese)
[12] 常楠, 杨伟, 王伟. 基于复合材料层板稳定性的铺层参数优化设计方法[J]. 机械强度, 2008, 30(1): 148-151.
Chang Nan, Yang Wei, Wang Wei. New method of ply optimization design for stability of composite laminates[J]. Journal of Mechanical Strength, 2008, 30(1): 148-151.(in Chinese)
