例析二项式定理中的数学思想

■山东省枣庄市第二中学 李景臣

数学思想始终伴随在数学学习和研究的过程中,蕴含在每一个知识板块中,学习数学就是要学习数学的解题思想以及解题方法,它们是数学的灵魂。二项式定理中包含着丰富的数学思想和方法,同学们在学习时,要善于回味、归纳、总结规律,从而提炼出数学思想方法,将知识转化为能力,使所学知识得以升华。在二项式定理的学习中,以下数学思想方法值得我们关注。

一、构造思想

例1 证明下列等式:

(1)

(2)

分析:此结构形式与二项式展开式相似,因而构造二项式求证。

证明:(1)在二项式定理中,令a=1,b=2,得(1+2)n=·22+…+,化简后为3n=1++…+,所证等式成立。

点拨:本题(1)用的是赋值法,而(2)用的则是一种构造法,在有关组合恒等式的证明中,常采用这种方法。

二、化归转化思想

例2 (1)求(1-x)3(1+x)10的展开式中x5的系数;

(2)x＞0的展开式中的常数项。

分析:本题的两小题都不是二项式展开式,但可以转化为二项展开式问题。(1)可以视为两个二项展开式相乘;(2)可以经过代数式变形转化为二项式。

解:(1)(1-x)3(1+x)10展开式中的x5可以看成是由下列几种方式得到,然后合并同类项:用(1-x)3展开式中的常数项乘(1+x)10展开式中的五次项,可以得到用(1-x)3展开式中的一次项乘(1+x)10展开式中的四次项可得到(-3x)·);用(1-x)3展开式中的二次项乘(1+x)10展开式中的三次项可得到3x2·;用(1-x)3展开式中的三次项乘(1+x)10展开式中的x2项可得到-x3·。合并同类项得含x5的项为:它为常数项,则r=6,常数项为C612=924。

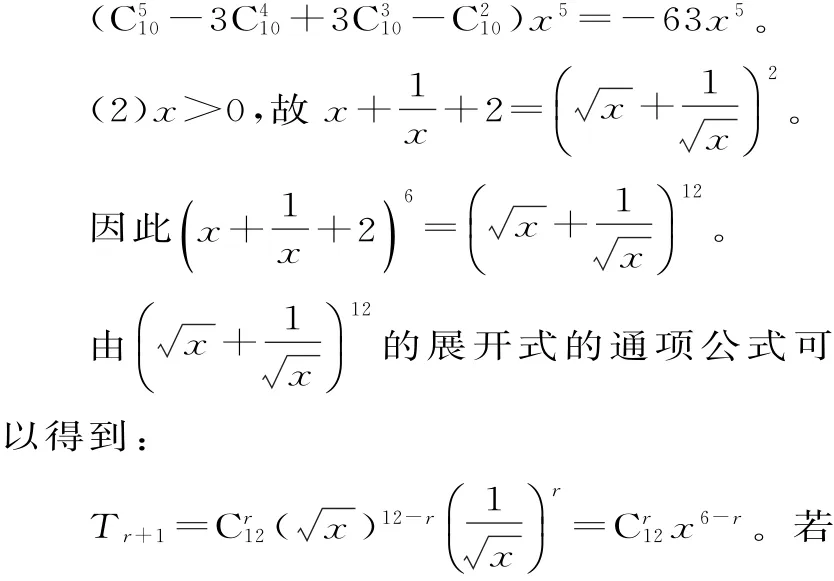
点拨:问题(2)中将非二项式通过因式分解化为二项式来解决。

三、分类讨论思想

例3 设数列{an}是等比数列,a1=的展开式中的第二项(按x的降幂排列)。

(1)用n,x表示通项an与前n项和Sn;

(2)若,用n,x表示bn。

分析:本题涉及数列、排列、组合、二项式定理等相关知识点。

所以公比q=x。

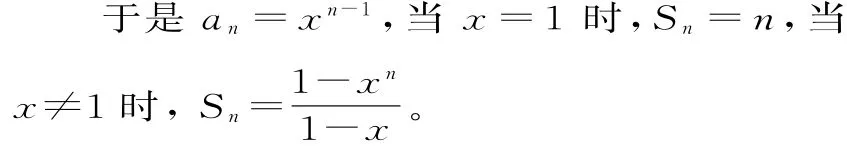
(2)当x=1时,…+nCnn。

又因为bn=n·

点拨:用倒序相加法及二项展开式解此类问题时不能忽视对字母的讨论。

四、放缩法

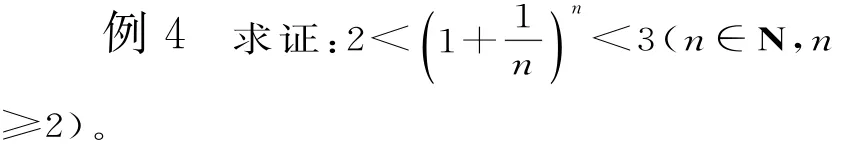
分析:利用二项展开式解题,注意到展开式的特点,结合放缩法,可以得证。

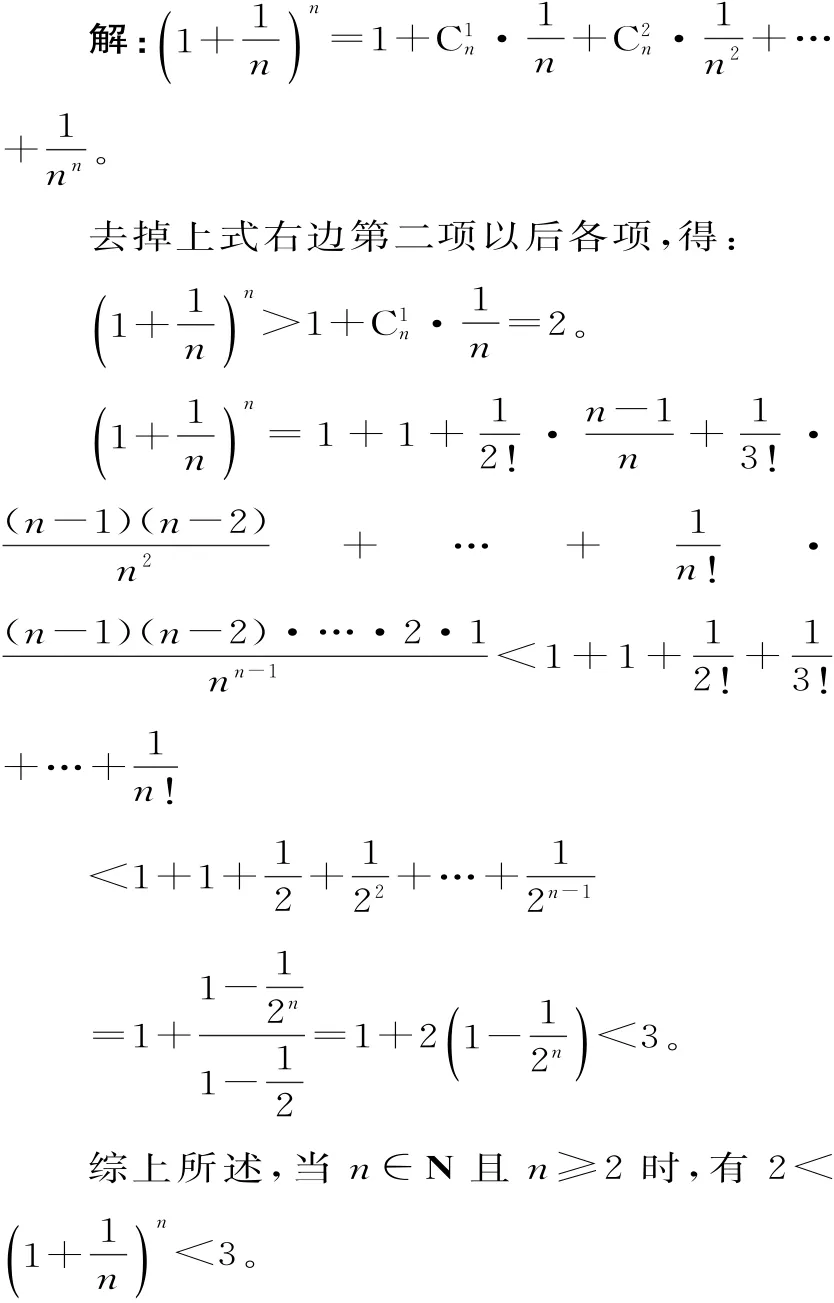
点拨:二项式定理起到的放缩作用是非常“巧妙”的,往往在一些不等式的证明中起着关键的作用,常常利用(1+x)n＞1+C1nx(x＞0)进行放缩。

五、函数与方程思想

例5 已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn。

若a1+a2+…+an-1=29-n,求n的值。

解析:a0=1+1+…+1=n,an=1。

令x=1,则:

2+22+23+…+2n=a0+a1+a2+…+an。

则2n+1-n-3=29-n,n=4。

点拨:在二项式定理的应用中,求系数的取值总是列出方程,通过赋值求解,把二项展开式看作x的函数f(x),其系数问题与函数值f(1)的展开式相联系。

六、整体思想

例6 在一项的系数最大?

分析:解决这类问题应注意二项式系数与项的系数的区别,令Ar,Ar+1分别为展开式的第r项和第r+1项的系数,仿照研究二项式系数的变化规律的方法,我们来研究展开式中各项系数的变化规律。

三、四项的系数最大。

点拨:二项式的通项公式是求某些特定项或二项式系数最大项的有力工具,此处用整体思想考虑问题,观察{An}的变化规律,做到胸中有全局,方向明确,脉络清楚,正确求得结果。

七、赋值法

例7 已知前三项系数的和为129,这个展开式中是否含有常数项?一次项?若没有,请说明理由;若有,请求出来。

分析:本题与展开式中的特定项有关,故可用通项公式解决。另外,本题还是一道探索类问题。

解:因为,r=0,1,2,…,n,所以由题意知=129。结合组合数公式,有1+2n+2n(n-1)=2n2+1=129,所以2n2=128,n2=64。

又n∈N*,所以n=8。因此

若展开式中存在常数项,则72-11r=0,得∉N*,所以展开式中不存在常数项。

若展开式中存在一次项,则所以72-11r=6,解得r=6。因此,展开式中存在一次项,它是第7项,T7=C68·26·x=C28·26x=1792x。

点拨:二项式定理主要涉及两个方面的问题:一方面是展开式中的某项或某项的系数,处理的方法是利用通项公式;另一方面是系数和的问题,处理的方法是赋特殊值法。