射流与超声速来流剪切层作用的数值模拟研究

邓放 韩桂来 刘美宽 丁珏 翁培奋 姜宗林

摘要：本文采用高精度格式求解二维Navier-Stokes方程，分别应用五阶WEND格式、六阶中心差分格式离散对流项和黏性项，时间推进采用三阶Runge-Kutta格式，并应用MPI非阻塞式通信进行并行计算，模拟了超声速射流与同向超声速流动的相互作用，目的在于研究流长产生的两个剪切层的相互作用，发现了有一定夹角的剪切层作用产生周期性次生射流的现象。本文研究了射流/超声速流剪切层相互作用、作用产生的次生射流具有脉冲性等方面，着重对次声射流的周期性等展开分析和讨论。

关键词：射流;剪切层;超声速;次声射流;数值模拟

中图分类号：V211 文献标识码：A

射流和超声速来流的组合流动是空气动力学的重要流动现象，两者之间相互作用非常普遍，如双模态超燃冲压发动机中，为增强气流和燃料的掺混，燃烧室中使用燃料喷注支板，以达到燃料与超声速气流混合的目的[1]。火箭发射过程中，喷管出口的超声速射流与箭体周围气流相互作用，并随着高度变化形成不同类型的射流特征[2-4];超声速巡航导弹在飞行过程中，发动机尾部喷管形成的射流与弹体周围气流形成相互作用[5]。因此，射流、超声速流动及其剪切层相互作用具有重要的工程实用背景和理论研究价值。

现阶段剪切层的研究主要集中采用凹腔、后台阶等模型：Stalling[6]等根据剪切层的再附形式的不同，最早将凹腔流动的形式分为开口式流动和闭口式流动;Michael[7]等在试验中发现不稳定模态下有超声速剪切层的大尺度卷吸涡结构。Shen[8]等通过大量试验测量及分析，将后台阶起始涡流的整个发展过程可以被归结为4个阶段：（1）第一加速阶段;（2）第二加速阶段;（3）第二诱导分离涡与第二分离涡阶段;（4）破碎阶段。Makoto[9]等使用数值模拟和试验的方法，研究了后台阶高度对剪切层再附长度的影响。

目前的很多研究还局限于剪切层与激波膨胀波作用、剪切层与边界层作用等领域，而没有合适的模型来研究剪切层与剪切层相互作用：Suzuki[10]等使用几何声学理论和DNS这两种方法研究了二维超声速剪切层与可压缩波弱激波膨胀波的相互作用问题，研究发现可压缩波在剪切层涡之间的鞍点处发生泄漏;Kobayachi T[11]等对不同的台阶入口速度分布情况在后台阶流动的影响进行了讨论。

本文在后台阶处构造了超声速来流与射流的剪切层相互作用的模型。分别应用五阶WEND格式[12]、六阶中心差分格式离散对流项和黏性项[13]，Steger-Warming流通量矢量分裂法[14]对特征值进行分裂，时间推进采用三阶精度Runge-Kutta格式[15]，借助高精度数值模拟手段，开展流场基本结构和流动规律研究。

1 物理和数学模型

1.1 射流与超声速来流作用的物理模型

射流與超声速来流作用的物理模型如图1所示。超声速来流经过后台阶时，在后台阶拐角处形成剪切层，称为来流剪切层。射流的上方也产生一剪切层，称为射流剪切层。由于射流剪切层和来流剪切层的相互作用，射流剪切层与超声速来流剪切层交汇处一些物质会从射流剪切层和来流剪切层之间射出，称为次生射流。来流剪切层和射流剪切层之间的区域为回流区。本文模拟了超声速后台流动/超声速射流相互作用下的流场结构，相应的边界条件见表1。射流出口马赫数为3，参数设置见表2。超声速来流马赫数为3，具体参数见表3。

1.2 控制方程

采用可压缩Navier-Stokes（N-S）方程作为流动控制方程，N-S方程采用来流参数进行无量纲化：

各矢量形式如下：式中：ρ和p分别为气体的密度和压力，u、v和w分别为x、y和z方向上的速度分量，为单位体积总能，采用理想气体状态方程p=ρRT，其中R₀=8.314J/（mol·K），Mair为气体的摩尔质量。

直角坐标系下的控制方程经过Jacobian变换之后，计算空间中的Navier-Stokes方程形式为：

各矢量形式如下：

式中，Jacobian行列式为：

各黏性应力分量如下：

各方向上的热流分量如下：

1.3 计算方法

对流项离散形式如下：

式中的矢通量构造如下：

其中：

式中：ω_xk⁺采用Jiang和Shu[16]建议的最佳权重系数为：式中：n为一个整数，通常取1或2，我们根据Jiang和Shu的建议，取n为2。而组合系数分别为：

G通量类似，轮换下标即可获得相应表达式。黏性项半离散逼近式为：

其中导数项可以离散表示为：

本文在时间积分上采用了三阶精度Runge-Kutta方法，计算公式为：

2 计算结果及分析

2.1 基本流动现象

在第一个台阶BC的上方，是马赫数Ma=3的超声速来流。回流区气流流动速度较小，回流再附到台阶下游表面的卷挟，来流方向的壁面边界层延伸形成超声速来流剪切层。

射流从EF处喷出，首先经过三角形状的等速核心区，其中温度、密度等都为常数，等速核心区外是射流边界层。气体的膨胀一方面使得气体加速并沿流向压力降低，另外一方面气体的过膨胀使得射流压力低于环境压力，导致射流在剪切层边界被压缩，形成反射激波或称拦截激波，射流边界和拦截激波之间为射流剪切层。

在超声速来流剪切层和射流剪切层的交汇处，会形成一股新的射流射入回流区，我们称为次生射流。研究发现，次生射流具有周期性，与剪切层的波动有关。当超声速来流剪切层的水平倾角达到一定高度时，新的次生射流射出;如果超声速来流剪切层的水平低于一定高度，次生射流将停止喷射。

在超声速来流剪切层和射流剪切层相互作用后，两个剪切层汇聚到一起，形成一股新的剪切层，称为混合剪切层。由于剪切层两侧的速度是不匹配的，因此它受到Kelvin-Helmholtz不稳定性的影响压力的波动对剪切层产生新的扰动，在混合剪切层两侧出现了微弱的激波群结构。这些微弱的激波被包裹在由两个剪切层相互作用形成的两个激波之间。

次生射流是由超声速来流剪切层和射流剪切层之间的相互作用产生的结构现象，同时，由于次生射流的射出，次生射流的前端会产生一道微弱的激波，我们称之为次生激波。如果次生激波向右移动，则次生激波的波前的超声速来流剪切层部分会被抬高。另一方面，如果次生激波向左移动，则次生激波的波前的超声速来流剪切层部分将被压下。在超声速来流剪切层的另一侧，二次冲击波也产生其自身的透射激波。如图2～图5所示。

由于次生激波和第二个台阶上壁面的作用，导致界面上产生Richtmyer-Meshkov不稳定性。如图6所示。我们可以发现在CD和DE的交界处存在明显的蘑菇结构，这些蘑菇结构是次生激波加速卷人壁面的射流剪切层的物质。

2.2 过膨胀射流和欠膨胀射流

我们研究了来流剪切层和射流剪切层的压比为0.6情况下的流场结构特点。射流压力低于环境压力，因此，此时的射流是过膨胀射流。过膨胀射流和超声速来流作用于第二个后台阶的位置，从而形成了复杂的流场结构。在0.1s的时间内，射流剪切层出现了振荡现象，在喷流剪切层和流入剪切层之间也不会产生次生喷流。这是因为如果射流是典型的过度膨胀射流，超声速来流剪切层提前失稳，超声速来流剪切层和射流剪切层相互作用微弱，此时则不会产生二次射流。

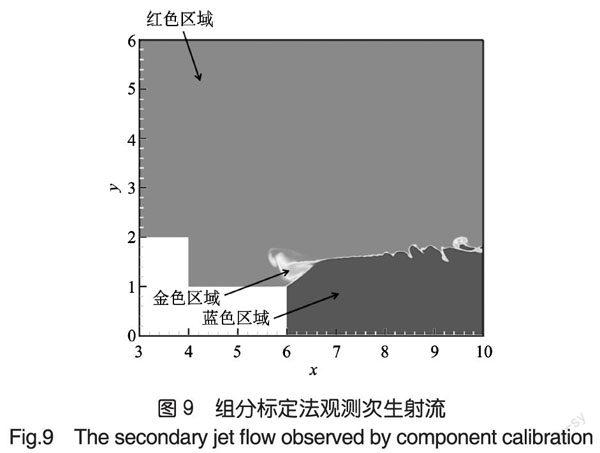
我们还研究了压比为1.2/2.5/10/30情况，在这5种情况下，射流的压力高于周围的压力，这表明此时的射流是典型的欠膨胀射流。首先，我们以压力比2.5为例。从0.01s到0.10s，如图7～图10所示，共有4个周期，每个周期约为0.021s。我们选择了第一个周期：从0.015～0.040s。利用组分标定的方法，第一个台阶上方的超声速流动被标注为蓝色，第二个台阶左端射出的射流标记为红色。如果射流剪切层和超声速来流剪切层之间物质的颜色变成金色，则意味着在回流区内喷入了超声速来流和射流的混合物质。这种方法可以很好地直观描述次生射流的产生过程。次生射流注入回流区后，射流水平倾角变小，射流剪切层压低，次生射流开始停止射入，随后射流剪切层再次抬高直到新的次生射流射入，新的周期产生，从而循环往复。

2.3 次生射流的周期性

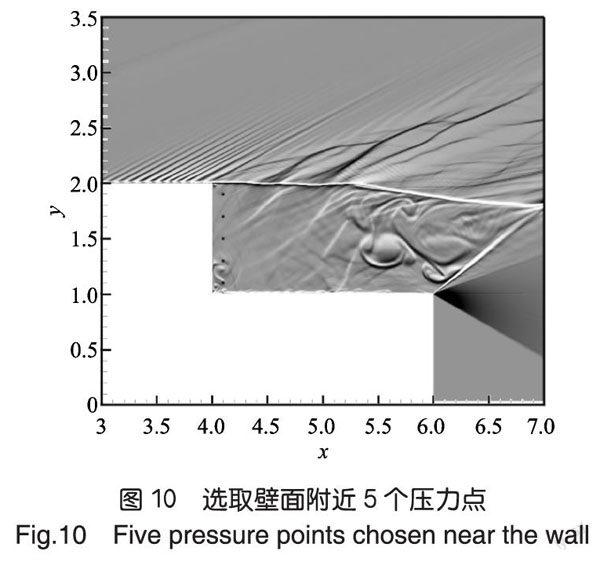
为了研究不同压力比对次生射流的影响，我们选择不同的压力比为2.5，10，30。由于次生射流对回流区压力变化有影响，我们选择图10所示的壁面5个压力点来观察次生射流的周期性。

如图11所示，这5个点的压力变化几乎是相同的频率，因此我们可以从数据角度准确觀察次生射流。

如图12（a）所示，我们可以准确观察4个周期的间隔。它们的周期大概在0.025s，周期频率在50Hz左右。这意味着当超声速来流和射流压比变大时，整个周期波动的频率几乎没有变化。由于射流剪切层局部也会震动，我们可以观察到主周期也有其他细微的波动，当压力比较小时，射流剪切层整体周期性波动的影响处于主导地位，同时，射流剪切层局部振动影响相对较小但存在。

然而，如图12（b）所示，当压力比为30时。除了主循环外，我们可以注意到有很大的波动性。压比变大时，射流剪切层局部振动影响变大，甚至超声速来流剪切层出现失稳现象。每个主循环大约为0.025s。即使压力比变化，压力点的周期不会改变。射流剪切层整体的震动形成了主要周期和次生射流。由于射流剪切层的局部振动和超声速来流剪切层可能会提前失稳，也会导致来流区壁面附近的压力变化。但是，我们仍然可以观察到完整的循环。尽管压力比变化，主循环仍然约为0.025s，周期频率约为50Hz。

次生射流的周期性与压力比变化之间存在一定的关系，但压比变大会使得剪切层失稳更加显着，这就导致了射流剪切层的局部振动和超声速来流剪切层的提前失稳。

3 结论

通过分析，可以得出以下结论：

（1）射流剪切层与超声速来流剪切层相互作用，由于相互作用产生次生射流和混合剪切层。两个弱的冲击波位于混合剪切层的两侧。由于混合剪切层两侧的速度不一致，混合剪切层受到Kelvin-Helmholtz不稳定性的影响，然后失稳形成一些Kelvin-Helmholtz涡旋。

（2）次生射流具有周期性。周期性与射流剪切层的整体振荡有关。回流区壁面附近的压力变化受三个因素影响：射流剪切层整体振动、射流剪切层局部振动、超声速来流剪切层提前失稳。其中，射流剪切层整体振动是回流区压力变化的主要因素。随着压比的增加，其他两个因素的影响也增强。这意味着压力的增加导致两个剪切层之间相互作用的增强。

（3）现有工况下次生射流的周期约为0.025s，频率约为50Hz。即使压力比发生变化，射流剪切层波动的主要周期基本保持不变。因此，次生射流的周期并不随压力比的变化而变化。

参考文献

[1]宋冈霖，田亮，江强，等.超燃冲压发动机支板热性能研究[J].推进技术，2013，34（06）：809-816.

[2]Reardon J E，Nelson H F.Rocket plume base heatingmethodology[J].Journal of Thermophysics and Heat Transfer，1994，8（2）：216-221.

[3]Ebrahimi H B.Numerical investigation of jet interaction in asupersonic freestream[J].Journal of Spacecraft and Rockets，2008，45（1）：95.

[4]Troyes J，Dubois I，Borie V，et al.Multi-phase reactivenumerical simulations of a model solid rocket exhaust jet[C]//42^ndAIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit，2006： 4414.

[5]Michael R.Infrared signature generation of airborne targets[R].Proceedings of the SPIE（50277-786X），1993：114-122.

[6]Stallings R L，Wilcox F J.Experimental cavity pressuredistributions at supersonic speeds[R].NASA TP-2683，1987.

[7]Kegerise M A，Spina E F，Garg S，et al.Mode-switching andnonlinear effects in compressible flow over a cavity[J].Physicsof Fluids，2004，16（3）：678-687.

[8]Shen G X，Ma G Y.The investigation on the properties andstructures of starting vortex flow past a backward-facing step byWBIV technique[J].Experiments in Fluids，1996，21（1）：57-65.

[9]Oki M，Iwasawa T，Suehiro M，et al.Numerical simulationwithout turbulence model for backward-facing step flow[J].JSME International Journal Series B：Fluids and ThermalEngineering，1993，36（4）：577-583.

[10]Suzuki T，Lele S K.Shock leakage through an unsteady vortex-laden mixing layer：Application to jet screech[J].Journal ofFluid Mechanics，2003，490：139-167.

[11] Kobayashi T，Togashi S.Comparison of turbulence modelsapplied to backward-facing step flow[J].JSME InternationalJournal Series B：Fluids and Thermal Engineering，1996，39（3）：453-460.

[12] Jiang G S，Shu C W.Efficient implementation of weighted ENOschemes[J]·Journal of Computational Physics，1996，126（1）：202-228.

[13]傅德薰，馬延文，李新亮.可压缩湍流直接数值模拟[M].北京：科学出版社，2010.

[14]Steger J L，Warming R F.Flux vector splitting of the inviscidgasdynamic equations with application to finite-differencemethods[J].Journal of Computational Physics，1981，40（2）：263-293.

[15]Dormand J R，Prince P J.A family of embedded Runge-Kutta formulae[J].Journal of Computational and AppliedMathematics，1980，6（1）：19-26.

[16]Jiang G S，Shu C W.Efficient implementation of weighted ENOschemes[J].Journal of Computational Physics，1996，126（1）：202-228.