基于SCMA系统的多用户检测消息传递算法
2018-05-30张雪婉葛文萍
张雪婉,葛文萍,吴 雄
(新疆大学 信息科学与工程学院,乌鲁木齐 830046)
0 概述
正交多址接入一直在前几代的电信系统中被广泛应用。为了满足未来5G的众多需求,IMT-2020推进组提出了非正交多址接入[1]。在众多非正交多址技术中[2],稀疏码多址接入(Sparse Code Multiple Access,SCMA)[3]作为第五代(5G)移动通信系统的候选技术之一,引起了众多研究者的注意。由低密度信号(Low Density Signal,LDS)[4-6]演进而来的SCMA,将高维调制与稀疏扩频融合在一起,直接把比特数据流映射为预先设定码本里的复数域多维码字[7],用以解决海量连接的系统过载情况[8-9]。与OFDMA相比,SCMA可以实现150%、200%,甚至更多的设备连接数[10]。
目前,如何降低SCMA系统解码的复杂度是SCMA面临的重要挑战之一[11]。在文献[7]中基于SCMA码本的稀疏性提到并行MPA算法。在此基础上,文献[8]提出一种基于对数域的并行MAX-LogMPA算法,该算法虽然检测性能不如并行MPA算法,但却大大降低了算法的复杂度,硬件实现更加容易。文献[12]对并行MPA算法进行了详细的阐述以及仿真验证,证明了其是一种低复杂度且性能可以逼近最优检测器的优良算法。另外,文献[13-14]也提出一种串行的MPA算法,该算法与并行MPA算法相比,加快了检测器的收敛速度,算法复杂度也有所降低。
针对以上不同策略的MPA多用户检测算法,本文结合串行MPA算法收敛速度快和并行MAX-Log MPA算法复杂度较低的优点,提出一种基于对数域的串行MAX-LogMPA算法。该算法可加快收敛速度,在保证BER性能的条件下其算法复杂度达到最低。
另外,考虑到现有研究大都采用基于并行MPA算法对SCMA系统进行多用户检测,还没有相关工作来对以上不同策略的MPA算法进行统一的性能比较和总结,本文对以上不同策略的MPA算法进行详细论述,并与最大似然(Maximum Likelihood,ML)算法进行性能比较。
1 上行SCMA系统模型
假定一个上行多用户SCMA通信系统,J个用户共享N个正交时频资源K(J>K),并传输数据给同一个基站,其过载因子定义为λ=J/K。J=6,K=4的上行SCMA系统模型如图1所示。
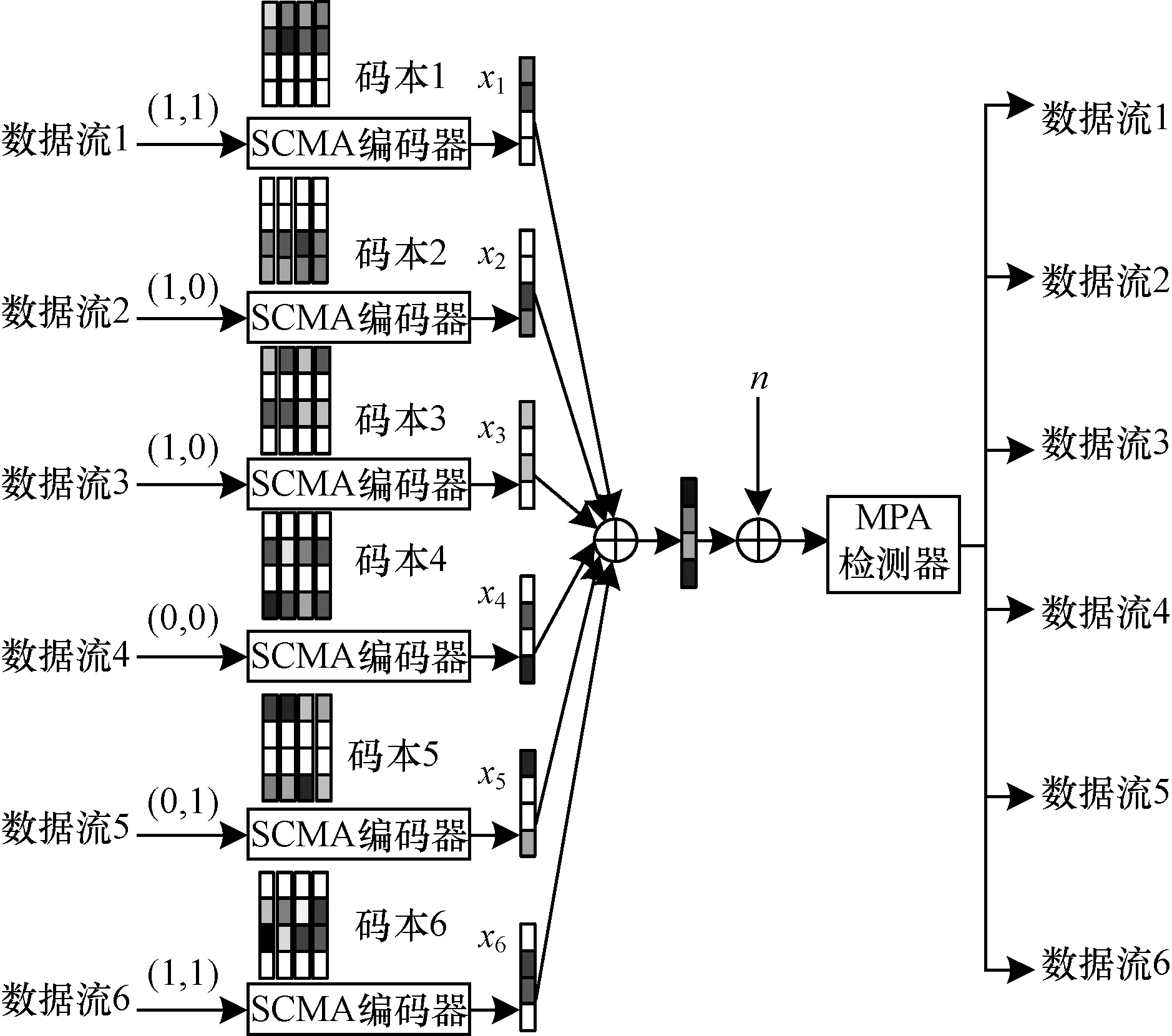
图1 上行SCMA通信系统模型
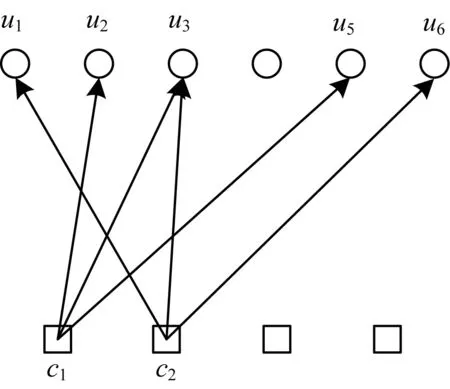
SCMA编码器定义为f:BlbM→X,x=f(b),其中X∈Ck,基数|X|=M。K维复数码字x是具有N 图2 矩阵F及因子图的对应关系 假定全部用户时间同步,基站接收到的信号为全部用户信号叠加,可以表示为: (1) 其中,xj=[x1j,x2j,…,xkj]T表示第j个用户发送的码字,hj=[h1j,h2j,…,hkj]T表示第j个用户的信道向量,n为高斯白噪声且n~cN(0,σ2I)。 时频资源k处接收到的信号为: (2) 由于码字xj是稀疏的,因此在时频资源k处仅有较少的码字冲突。 给定y为接收信号,并假定基站已经获取了信道矩阵H=(h1,h2,…,hj),则针对于X=(x1,x2,…,xj)的联合最大后验概率检测可以表示为: (3) (4) 如果假设每个码字的发射概率都相等,那么最大后验概率检测MAP就简化成最大释然检测ML: (5) ML算法利用穷举法搜索所有用户以及各自码本的可能组合,所以算法复杂度极高,这就限制了其在实际通信系统的应用[14]。 由于SCMA通信系统的码字稀疏性特点,基于和积算法[15]原理,次优的基于迭代的低复杂度的MPA算法被提出[7]。作为SCMA系统中主流的多用户检测算法,MPA算法具有无法替代的优势。 图3 并行MPA算法的消息传递过程 并行MPA一次迭代过程中的2个阶段可以分别用数学公式表示为: (6) (7) 其中,t为迭代次数,εk与ζj分别表示稀疏码矩阵F第k行的非零位置集与第j列的非零位置集。 并行MPA达到预先设定的最大迭代次数tmax后,每一个用户各自的码字输出概率可以表示为: (8) 得到每个用户各自的码字概率以后,接下来就需要算出对数似然比(Log Likelihood Rate,LLR),每一个bit的LLR(bj,m)可表示为: (9) 其中,m=1,2,…,lb(Q),Q为使用的调制进制数。 最后,判决LLR(bj,m)得到bj,m,判决表达式: (10) 与ML算法相比,该算法由于利用了SCMA的稀疏性这一特点,节点之间的信息在递送过程时,只考虑与自身相连的节点,因此算法复杂度有所减低,性能接近ML算法。但该算法收敛速度较慢。 (11) 由式(11)可以看出,用户节点的计算可以由资源节点计算得出,即资源节点与用户节点的计算公式可以合二为一。 (12) 其中,[.]old与[.]new分别表示更新前后的消息。显然Pt-1(xj)的置信度,[Pt-1(xj)]new比[Pt-1(xj)]old更准确。例如k=1,k=2时,串行MPA算法的迭代过程如图4所示。因为用户u3对应于2个资源节点,在k=1计算完以后,由式(12)可知,用户u3的置信度也随之改变,当进行下次计算,即k=2时,参与运算的用户u3已经是更新后的新消息。所以该算法在每次计算时同时伴随用户码字消息的更新,为下一步的计算提供了更加可靠的置信度。 图4 串行MPA算法的信息传递过程 (13) 综合式(6)和式(13),可以得到串行 MPA多用户检测算法的资源节点消息更新公式为: (14) 其中,i≠j,i∈εk,j∈εk。 串行 MPA多用户检测算法在每轮迭代过程中,更新后的消息马上传递给后面的节点,而不必等到下一轮迭代过程。显然,这种串行策略对消息的更新是异步的,并且越靠后处理的资源节点消息更新越可靠。这样一来,串行MPA进行一次迭代相当于并行MPA多次迭代的效果,改善了消息收敛特性。显然,在较少迭代次数时,串行 MPA在误码率性能上的优势更能得到体现。 由于exp()以及连乘计算的复杂性,通过取对数的运算,并采用max近似计算资源节点的信息更新,可以大幅度地降低计算的复杂度。该算法的计算公式如下: 因为: (15) 所以,式(6)和式(7)可以改写为: (16) (17) 达到预先设定的最大迭代次数tmax后,每一个用户各自的码字输出概率可以表示为: (18) 从式(15)和式(16)可以看出,节点在迭代更新的过程中,由于采用了max的近似计算,必将造成一部分的信息丢失,因此该算法的性能一定不如前2种算法。另外,从式(16)~式(18)可以发现,通过取对数运算,把乘法转化为加法,在实际计算时,乘法器将减少,加法器增加,这样将使算法复杂度降低。所以,该算法是以牺牲检测性能来降低运算复杂度,在误码率可以容忍的情况下,运算复杂度使硬件的实现变得更加容易。 由2.2节对串行MPA的分析和2.3节对并行MAX-Log MPA的分析可知,串行MPA算法具有收敛速度快的优点,MAX-Log运算可以降低复杂度。为了进一步降低运算复杂度,本文提出一种串行MAX-Log MPA算法。 对式(13)和式(14)取MAX-Log运算,可以得到串行MAX-Log MPA多用户检测算法用户码字和资源节点消息更新公式: (19) (20) 该算法由于继承了串行策略在收敛速度方面的优势,在每轮迭代过程中,更新后的消息能立刻传递给后面的节点,用于下一资源节点的消息更新,而不必像并行MAX-Log MPA必须等到下一轮迭代过程,并且越靠后计算的资源节点消息更新越可靠。这样平均下来,串行MAX-Log MPA进行一次迭代相当于并行MAX-Log MPA多次迭代的效果,在迭代次数较少时,串行MAX-Log MPA比并行MAX-Log MPA在误码率性能上更有优势。 SCMA多用户检测算法的复杂度主要体现在迭代计算过程和迭代次数[8,13-14]。与并行MAX-Log MPA相比,本文算法是通过收敛所需要迭代次数的减少来进一步降低计算复杂度。 以算法达到收敛所涉及的乘法器、加法器、exp运算数目为标准分析复杂度。由理论分析可知,串行MPA比并行MPA在收敛速度上更有优势,在算法达到收敛,整个多用户检测过程所需的加法器、乘法器会相应减少。同理,算法达到收敛,串行MAX-Log MPA比并行MAX-Log MPA所需的加法器、乘法器也会减少。另外,由文献[10]可知,并、串MPA中的exp()运算会增加大量的计算复杂度和消耗不少的存储空间。由此可知,串行MAX-Log MPA既加快了收敛速度,又采用MAX-Log运算消除了exp()运算,其复杂度进一步降低。 另外,为了对以上基于不同策略的MPA算法进行复杂度分析,列出5种算法的复杂度,如表1所示。式中df表示作用于资源节点的用户数,dv表示作用于用户节点的时频资源数。 表1 不同策略实现的MPA算法以及最优ML算法运算复杂度 为了验证本文所提算法在上行SCMA通信系统的性能和分析基于不同策略实现的MPA算法的性能,将以上算法进行比较仿真实验。仿真参数为用户数J=6、扩频因子K=4、码本尺寸M=4、过载率λ=150%,信道类型为加性高斯白噪声AWGN。 图5是信噪比为12 dB时,4种采用不同策略实现的MPA算法的收敛情况。由图5可以看出,串行MPA和串行MAX-Log MPA多用户检测算法(3次达到收敛),其收敛速度比起并行MPA和并行MAX-Log MPA多用户检测算法(6次达到收敛)快上1倍。在迭代次数较小(1次、2次与3次)的情况下,串行MPA和串行MAX-Log MPA的误码率性能明显优于并行MPA和并行MAX-Log MPA,这是因为串行MPA和串行MAX-Log MPA可以立即把已更新的消息传递给后面的节点,而不像并行MPA和并行MAX-Log MPA那样必须等到下一轮的迭代,这就使得采用串行策略的算法可以更加充分地利用新信息,从而加快算法的收敛速度。另外,无论是并行MPA、串行MPA,还是并行MAX-Log MPA、串行MAX-Log MPA,在算法最终达到收敛后,并、串行MPA的最终误码率性能一致,并、串行MAX-Log MPA的最终误码率性能一致。这是因为无论哪种策略最终都能充分利用已更新的消息。 图5 4种不同策略的MPA算法收敛速度 并、串MAX-Log MPA与并、串MPA相比,其误码率性能降低了约一个数量级。这是因为并、串MAX-Log MPA采用MAX近似计算节点之间的消息更新,会造成一部分信息的丢失,置信度降低,所以在最终算法到达收敛后,其误码率性能也会降低。由此可以看出,本文算法误码率性能与并行 MAX-Log MPA相当,但由于继承了串行策略使其收敛速度加快了近1倍。 图6为4种不同策略的MPA算法以及最优ML算法误码率性能的比较,图中误码率性能是不同策略的MPA算法达到收敛以后的误码率性能。由图6可知,并、串行MAX-LogMPA两者收敛后的误码率性能一样,且随信噪比的增大,误码率呈线性下降的趋势。并、串MPA两者的误码率性能较好,且误码率性能也完全一致,随信噪比的增大,误码率呈指数下降的趋势。最优ML算法的误码率性能,在信噪比小于2 dB时还不如并、串MAX-Log MPA,信噪比小于4 dB。在信噪比大于4 dB时,ML算法的误码率优势开始显现出来,在所有算法中误码率性能最优。所以说,在环境很差的条件下,ML算法并不是最优的。另外,并、串行MPA算法的误码率性能与最优ML算法的误码率性能相近。 图6 4种不同策略的算法误码率性能比较 结合算法复杂度分析和3次迭代串行MPA、串行MAX-Log MPA,6次迭代并行MPA、并行MAX-Log MPA,可以得到图7。从图中可知,最优ML算法复杂度最高,硬件难以实现。针对并、串MPA算法,由于串行MPA算法的收敛速度快,算法的复杂度相对于并行MPA算法更低。虽然并、串MPA算法的复杂度比ML算法降低了2倍~3倍,但算法复杂度依然保持在104的数量级,硬件实现并不容易。并、串MAX-Log MPA虽然误码率性能有所降低,但其算法复杂度却是最低的,除了加法器和乘法器以外,也不存在特别复杂的函数运算。另外,对比这5种算法,本文提出的基于对数域的串行MAX-LogMPA算法不但继承了MAX-Log运算低复杂度的特点,又继承了串行策略收敛速度快的特性,其算法复杂度比并行MAX-Log MPA更低,是5种算法中最低的,硬件实现也更加容易。 图7 不同策略的算法运算复杂度对比 本文对采用不同策略的MPA算法进行阐述,并结合串行MPA算法和MAX-Log运算两者之间的优点,提出一种串行MAX-LogMPA算法。通过对收敛速度、误码率性能、算法复杂度3个方面的仿真实验对比,可以发现:采用串行MPA与并行MPA的误码率性能一样;并、串MAX-Log MPA两者的误码率性能相对较差,算法复杂度低,硬件实现容易。综合来看,串行MPA算法比并行MPA多用户检测算法更优。串行MAX-LogMPA算法的算法复杂度进一步降低,硬件实现更加容易。 [1] SOLDANI D,MANZALINI A.Horizon 2020 and beyond:on the 5G operating system for a true digital society[J].IEEE Vehicular Technology Magazine,2015,10(1):32-42. [2] WANG Bichai,WANG Kun,LU Zhaohua,et al.Comparison study of non-orthogonal multiple access schemes for 5G[C]//Proceedings of IEEE International Symposium on Broadband Multimedia Systems and Broadcasting.Washington D.C.,USA:IEEE Press,2015:1-5. [3] NIKOPOUR H,BALIGH H.Sparse code multiple access[C]//Proceedings of IEEE International Symposium on Personal Indoor and Mobile Radio Communications.Washington D.C.,USA:IEEE Press,2013:332-336. [4] HOSHYAR R,WATHAN F P,TAFAZOLLI R.Novel low-density signature for synchronous CDMA systems over AWGN channel[J].IEEE Transactions on Signal Processing,2008,56(4):1616-1626. [5] BEEK J V D,POPOVIC B M.Multiple access with low-density signatures[C]//Proceedings of IEEE Global Telecommunications Conference.Washington D.C.,USA:IEEE Press,2009:1-6. [6] RAZAVI R,HOSHYAR R,IMRAN M A,et al.Information theoretic analysis of LDS scheme[J].IEEE Communications Letters,2011,15(8):798-800. [7] TAHERZADEH M,NIKOPOUR H,BAYESTECH A,et al.SCMA codebook design[C]//Proceedings of IEEE Vehicular Technology Conference.Washington D.C.,USA:IEEE Press,2014:14-17. [8] ZHANG Shunqing,XU Xiuqiang,LU Lei,et al.Sparse code multiple access:an energy efficient uplink approach for 5G wireless systems[C]//Proceedings of IEEE Global Telecommunications Conference.Washington D.C.,USA:IEEE Press,2014:4782-4787. [9] AU K,ZHANG Liqing,NIKOPOUR H,et al.Uplink contention based SCMA for 5G radio systems[C]//Proceedings of IEEE Global Telecommunications Con-ference.Washington D.C.,USA:IEEE Press,2014:900-905. [10] LU Lei,CHEN Yan,GUO Wenting,et al.Prototype for 5G new air interface technology SCMA and performance evaluation[J].China Communications,2015,12(s1):38-48. [11] DU Yang,DONG Binhong,CHEN Zhi.Joint sparse graph-detector design for downlink MIMO-SCMA system[J].IEEE Journals & Magazines,2017,6(1):14-17. [12] WU Yiqun,ZHANG Shunqing,CHEN Yan.Iterative multiuser receiver in sparse code multiple access systems[C]//Proceedings of IEEE International Conference on Communications.Washington D.C.,USA:IEEE Press,2015:2918-2923. [13] DU Yang,DONG Binhong,CHEN Zhi,et al.A fast convergence multiuser detection scheme for uplink SCMA systems[J].IEEE Wireless Communications Letters,2016,5(4):388-391. [14] 杜 洋,董彬虹,王显俊,等.基于串行策略的SCMA多用户检测算法[J].电子与信息学报,2016,38(8):1888-1893. [15] KSCHISCHANG F R,FREY B J,LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions onInformation Theory,2001,47(2):498-519.
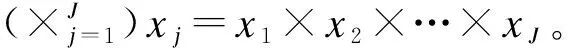
2 消息传递算法
2.1 并行MPA


2.2 串行MPA

2.3 并行MAX-Log MPA
2.4 串行MAX-Log MPA
3 算法复杂度分析

4 仿真分析
4.1 收敛速度
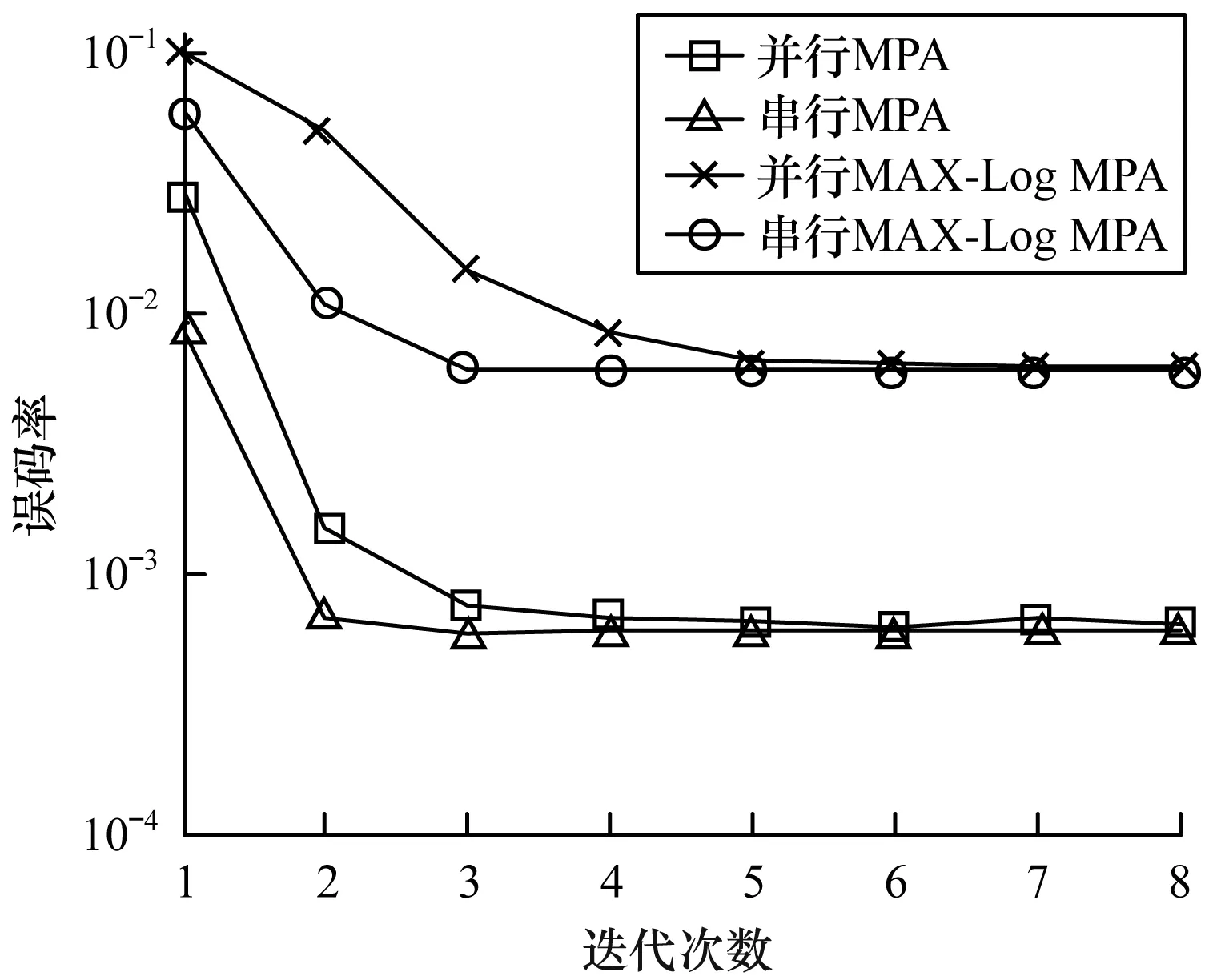
4.2 误码率性能对比

4.3 算法复杂度对比

5 结束语
