2018 年高考《选修3—3》命题趋势剖析

2018-05-30江西省南康中学彭长礼

中学生数理化(高中版.高考理化) 2018年5期

■江西省南康中学彭长礼

高考对《选修3—3》模块内容的考查题型以选择与填空相结合或以选择与计算相结合的形式呈现，其中计算题以对气体实验定律的考查为主，虽然综合性不太强，但容易失分，同学们在复习备考过程中应加以重视。同学们在高三复习的最后阶段应强化基本概念、规律的记忆、理解及应用，建立宏观量与微观量的关系。

命题特点：以选择题的形式考查分子动理论、气体压强的微观解释、晶体和非晶体的特点、液体的表面张力、饱和蒸汽与饱和蒸汽压、热力学第二定律的理解等;以计算和问答题的形式结合气体考查内能、气体实验定律、理想气体的状态方程、热力学第一定律等;考查油膜法测分子直径的实验原理、操作步骤和数据处理等。

命题热点：(1)分子动理论要点，分子力、分子大小、质量、数目估算;(2)内能的变化、改变内能的物理过程，以及气体压强的决定因素;(3)理想气体的状态方程和用图像表示气体状态的变化;(4)热现象实验与探索过程的方法。

命题趋势：预计2018年高考对本部分内容将着重考查热学基础知识与气体实验定律的组合，热力学第一定律与气体实验定律的综合;考查对热现象的自主学习和创新能力，以科技前沿、社会热点及与生产生活相联系的问题为背景来考查热学知识在实际中的应用等。

本部分内容琐碎、知识点多，同学们在复习备考过程中应从微观角度分析固体、液体、气体的性质，以气体实验定律为主干，梳理出知识点，进行理解性记忆，同时对热点题型进行针对性训练。总之，要抓基础，重全面，防止遗漏知识要点。

一、分子动理论要点、内能的理解

例1我国已开展空气中PM2.5浓度的监测工作。PM2.5是指空气中直径等于或小于2.5μm的悬浮颗粒物，其飘浮在空中做无规则运动，很难自然沉降到地面，人体吸入后将形成危害。矿物燃料燃烧的排放物是形成PM2.5的主要原因，下列关于PM2.5的说法正确的是( )。

A.PM2.5的大小比空气中氧分子大得多

B.PM2.5在空气中的运动属于分子的热运动

C.PM2.5的运动轨迹只是由大量空气分子对PM2.5无规则碰撞的不平衡决定的

D.倡导低碳生活，减少煤和石油等燃料的使用，能有效减小PM2.5在空气中的浓度

E.PM2.5必然有内能

解析：PM2.5的尺寸比空气中氧分子的尺寸大得多，选项A正确;PM2.5在空气中的运动不属于分子的热运动，选项B错误;PM2.5的运动轨迹是由大量空气分子对PM2.5无规则碰撞的不平衡和气流的运动决定的，选项C错误;倡导低碳生活，减少煤和石油等燃料的使用，能有效减小PM2.5在空气中的浓度，PM2.5必然有内能，选项D、E正确。答案为ADE。

点评：通过审题明确“PM2.5是悬浮颗粒物”是解题的关键，其直径2.5μm远大于分子的直径(分子直径的数量级为10-10m)。

例2如图1所示为由两分子组成的系统的势能Ep与两分子间距离r的关系曲线，下列说法正确的是____。

图1

A.当r>r2时，分子间作用力表现为引力

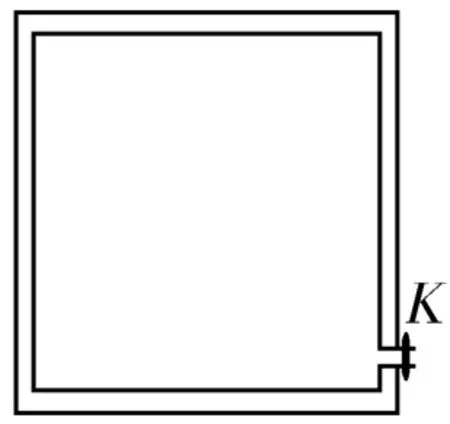
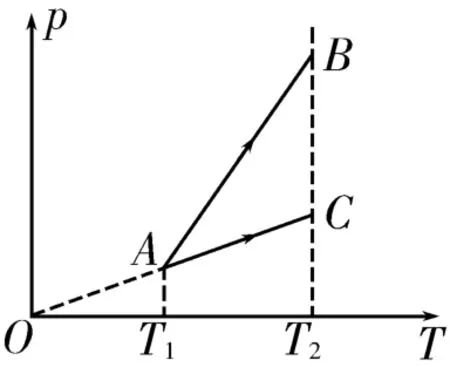
B.当r

C.当r=r2时，分子间作用力最大

D.在r由r1到r2的过程中，分子间作用力做负功

E.当r=r2时，分子势能最小

解析：(1)分子间距离为r2时分子势能最小，此时分子间的距离为平衡距离，即分子所受的引力与斥力大小相等。当0r2时分子间作用力表现为引力，故选项A、B正确。当r=r2时，分子间作用力为零，故选项C错误。在r由r1到r2的过程中，分子间作用力表现为斥力，分子间距离增大，分子间作用力做正功，分子势能减小，故选项D错误。因为当r>r2时分子间作用力表现为引力，随着分子间距离增大，分子间作用力做负功，分子势能增大，所以当分子间距离r=r2时分子势能最小，选项E正确。答案为ABE。

二、三个气体实验定律和理想气体的状态方程

1.气体实验定律(见表1)。

表1

2.理想气体的状态方程。

(1)理想气体状态方程的内容：一定质量的某种理想气体发生状态变化时，压强跟体积的乘积与热力学温度的比值保持不变。

(2)理想气体状态方程的表达式：(C是与p、V、T均无关的恒量)。

(3)运用气体实验三定律和理想气体的状态方程解题的基本思路：

①选对象——根据题意，选出所研究的某一部分气体，这部分气体在状态变化过程中，其质量必须保持不变。

②找参量——找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值，压强的确定往往是个关键，常常需要结合力学知识(如力的平衡条件或牛顿运动定律)才能写出表达式。对于涉及多个研究对象的问题，应注意分别确定每个对象的初、末状态三参量，并且用不同的下标区分开，防止张冠李戴。

③认过程——过程表示两个状态之间的一种变化方式，除题中条件已直接指明外，在许多情况下，往往需要通过对研究对象与周围环境的相互关系进行分析才能确定。

④列方程——根据研究对象状态变化的具体方式，选用理想气体的状态方程或某一气体实验定律，代入具体数值进行计算，注意T必须用热力学温度，p、V的单位要统一。

⑤验结果——由方程组解答出结果后，不要急于下结论，而要分析所得结果的合理性及其是否有实际的物理意义。

例3农村常用来喷洒农药的压缩喷雾器的结构如图2所示，药筒A的容积为7.5L，装入药液后，药液上方空气的体积为1.5L，关闭阀门K，用打气筒B每次打进1×105Pa的空气250mL，求：

图2

(1)要使药液上方的气体压强达到4×105Pa，打气筒活塞应打气的次数。

(2)当药筒A中有4×105Pa的气体后，打开阀门K可喷射药液，直到不能喷射时，喷雾器内剩余药液的体积。

解析：(1)用V表示打气前药液上方的体积，p0表示打气前药筒A内的气体压强，V0表示每次打入压强为p0的空气的体积，p1表示打入n次气体后药筒A内的气体压强，以药筒A中原有空气和n次打入药筒A内的全部气体为研究对象，由玻意耳定律得p0(V+nV0)=p1V，解得n=18。

(2)打开阀门K后，直到药液不能喷射，忽略喷管中药液产生的压强，则药筒A内的气体压强应等于外界大气压强，以药筒A内的气体作为研究对象，由玻意耳定律得p1V=p0V'，解得因此药筒A内剩余药液的体积ΔV=V总-V'=1.5L。

点评：本题是以农业生产工具喷雾器的工作原理为背景，从实际的角度考查气体实验定律，这是今后高考命题的方向之一。

例4如图3所示，下端带有阀门的汽缸内封闭有一定质量的理想气体，开始时汽缸内气体的压强等于大气压强p0，温度t=7℃。

图3

(1)关闭汽缸底部的阀门K，使缸内气体温度升高至t'=87℃，试计算此时缸内气体的压强。

(2)保持缸内气体温度始终为87℃，打开汽缸底部的阀门，缓慢放出部分气体，使缸内气体的压强再次等于大气压强p0，试计算此时缸内剩余气体的质量与原来气体总质量的比值。

解析：(1)此过程中缸内气体做等容变化，设升温后缸内气体的压强为p，由查理定律得，解得

(2)此过程中缸内原有气体做等温变化，设汽缸的体积为V0，当压强再次等于大气压强p0时，原有气体的体积为V，由玻意耳定律得pV0=p0V，解得。设此时气体的密度为ρ，则缸内剩余气体的质量m=ρV0，原来气体的总质量M=ρV，所以缸内剩余气体的质量与原来气体总质量的比值

三、气体压强的分析

例5一端封闭的粗细均匀的玻璃管中有一段16cm长的水银柱将空气封入管内，如果把玻璃管放在倾角θ=30°的斜面上，如图4所示。已知玻璃管与斜面间的动摩擦因数，外界大气压强p0= 76cmHg，当玻璃管沿斜面下滑时，封闭气体的压强为多少?

图4

解析：计算气体压强是解决气体问题的一个关键点，基本方法是以封闭气体的液柱(活塞、缸体等)为力学研究对象，分析受力，列出牛顿第二定律方程(静止时，则a=0)即可求解。设水银柱和玻璃管的质量分别为m和M，以水银柱和玻璃管为研究对象，根据牛顿第二定律得(m+M)gsinθ―μ(m+M)gcosθ=(m+M)a，解得。以水银柱为研究对象，设玻璃管的横截面积为S，根据牛顿第二定律得p0S+mgsinθ―pS=ma，又有m=ρlS，l=16cm，p0=76cmHg，解得管内封闭气体的压强80cmHg。

点评：对于静止情形，常用到初中物理学到的流体知识。①静止液体的压强公式p=ρgh;②当液面与外界大气压接触时，静止液体深h处的压强p=p0+ρgh;③帕斯卡定律，加在密闭液体上的压强，能够大小不变地由液体向各个方向传递;④连通器原理，连通的同一种液体中同一水平面上的压强相等;⑤利用“液片”分析压强。

四、固体与液体的性质

分析近三年的高考试题可以发现，固体和液体的性质也是高考常考的内容之一，考查的角度有：固体的微观结构、晶体和非晶体、液晶的微观结构、液体的表面张力、未饱和汽和饱和汽、饱和汽压、相对湿度等，命题的形式以选择题为主，难度不大。

例62013年6月20日我国女航天员王亚平在“天宫一号”上进行我国第一次太空授课，她不断用注射器向金属圆圈中的水膜里注入水，最后水膜变成了水球，分析形成水球的原因是 ( )。

A.水球在完全失重环境下不受任何力的作用

B.水球所受的地球对它的引力只改变它的运动状态，对其形状无影响

C.对水球形状有影响的是水的表面张力，在其向各个方向大小相同的表面张力的作用下形成球体

D.以上说法均不正确

解析：水球在“天宫一号”中要受到万有引力和表面张力的作用，选项A错误;水球所受的地球对它的引力全部用来产生向心加速度从而改变水球的运动状态，对其形状无影响，选项B正确;由于各个方向大小相同的表面张力的作用，才能形成球体，选项C正确;选项D错误。答案为BC。

五、热力学第一定律的理解及应用

例7在如图5所示的坐标系中，一定质量的某种理想气体先后发生以下两种状态变化过程：第一种变化是从状态A到状态B，外界对该气体做的功为6J;第二种变化是从状态A到状态C，该气体从外界吸收的热量为9J。已知线段AC的反向延长线过坐标原点O，B、C两状态的温度相同，理想气体的分子势能为零。

图5

(1)从状态A到状态C的过程中，求该气体对外界做的功W1，以及其内能的增量ΔU1。

(2)从状态A到状态B的过程中，求该气体内能的增量ΔU2，以及其从外界吸收的热量Q2。

解析：(1)从状态A到状态C的过程中，气体发生等容变化，该气体对外界做的功W1=0。根据热力学第一定律得ΔU1=W1+Q1，故该气体内能的增量ΔU1=Q1=9J。

(2)从状态A到状态B的过程中，气体的体积减小，温度升高，该气体内能的增量ΔU2=ΔU1=9J，根据热力学第一定律得ΔU2=W2+Q2，解得Q2=ΔU2-W2=3J。

点评：判定物体内能变化的方法包括以下四种。(1)判断内能的变化都要用热力学第一定律进行综合分析。(2)判断做功情况要看气体体积的变化情况。体积增大，气体对外做功，W为负;体积缩小，外界对气体做功，W为正。(3)与外界绝热，则不发生热传递，此时Q=0。(4)如果研究对象是理想气体，则由于理想气体没有分子势能，所以当它的内能变化时，主要体现在分子动能的变化上，从宏观上看就是温度发生了变化。

六、热力学定律与气体实验定律的综合

1.选取研究对象：研究对象可以是由两个或多个物体组成的系统，也可以是全部气体或某一部分气体(状态变化时，所选研究对象的质量必须一定)。

2.两类分析：(1)气体实验定律，确定状态参量，找出状态变化前后的p、V、T数值或表达式;(2)热力学定律，①做功情况，②吸、放热情况，③内能变化情况。

3.选用规律列出相关方程求解并检验。

例8如图6所示为一定质量的理想气体发生状态变化时的压强—温度(p-T)图像，已知气体在状态A时的体积为2L。

图6

(1)求气体在状态B、C时的体积。

(2)若气体从状态C到状态A的过程中，放出的热量为1500J，则此过程中气体的内能变化量为多少?

解析：(1)由p-T图像可知，气体从状态C到状态A发生等压变化，根据盖-吕萨克定律得，即，解得VC= 12L。气体从状态A到状态B发生等容变化，因此气体在状态B时的体积也为2L。

(2)因为从状态C到状态A的过程中，气体的体积减小，所以外界对气体做功，且做的功W=pΔV=1×105×(12-2)×10-3J=1000J。根据热力学第一定律可知，气体的内能变化量 ΔU=1000J-1500J=-500J，即气体的内能减少了500J。

例9如图7所示，一个绝热的汽缸竖直放置，内有一个绝热且光滑的活塞，中间有一个固定的导热性能良好的隔板，隔板将汽缸分成两部分，分别密封着两部分理想气体A和B，活塞的质量为m，横截面积为S，与隔板相距为h。现通过电热丝缓慢加热气体，当气体A吸收热量Q时，活塞上升了h，此时气体的温度为T1。已知大气压强为p0，重力加速度为g。