基于经纬度的航迹数据改进抗野值Kalman滤波∗

鱼佳欣 冯建锋 李文君 郭 然

（中国洛阳电子装备试验中心 济源 459000）

1 引言

在靶场试验过程中，使用雷达、GPS等对被试目标进行跟踪测量，但在测量过程中，由于电磁干扰、遮挡（如建筑、林荫）以及载体机动等异常情况，测量序列中常常会出现严重偏离目标真值的数据，称为“野值”。即使是高质量的原始采样数据，也会含有1%～5%甚至多达10%～20%的异常数据［1］。野值分为单点野值与连续野值，其特点一般是幅值大、持续时间短、无规律。如果不予以分离和滤除这些野值，指挥员无法准确判断目标位置，影响试验的顺利开展，具有一定的危险性，而且给后期的数据处理带来误差［2］。

由于航迹测量数据解算属于实时目标跟踪测量，被测量对象在测量过程中不断变化，且每一观测点只进行一次观测。因此，静态重复测量的检验准则不适于测量数据的合理性检验，所以应选择实时抗野值修正方法。

目前，在实时目标跟踪中辨识与剔除测量数据野值方面，已提出许多算法。本文研究了三种方法：简单经纬度法、最小二乘法和抗野值Kalman滤波方法，并对后者进行改进，试验结果表明了各算法的优势和劣势。

2 实时抗野值的修正方法

2.1 简单经纬度法

简单经纬度法思路为：应用式（1）、（2）比较实时测量的相邻数据点的经纬度值，式中JDFilter和WDFilter为过滤阈值，其大小由测量设备的性能决定。若满足条件则认为第n+1的值是真值，否则认为是野值丢弃。其算法原理图如图1：

图1 简单经纬度法和改进简单经纬度法原理图

简单经纬度法有个缺陷，当收到第一个测量值是野值，那给后来的数据判断提供了错误导向，导致正确的真值也被认为是野值滤掉。为此，本文在简单经纬度法基础上提出改进措施：如图1中的红色椭圆中标注，即增加了对第一个测量值的判断，如果不满足式（1）～（2），则将第n和第n+1的值均删除，直至满足条件。这样在一定程度上确保了收到的第一个值为真值，为后期的判断提供了较准确的基础。

改进后的简单经纬度法仍有个缺陷，当野值大量间隔出现时，会滤掉较多真值，短时间内无法得知目标实时位置。

2.2 最小二乘法

要克服野值间隔出现，则需利用收到的多个值进行过滤。最小二乘法的思路是：利用最后收到的4个点迹数据Un-1、Un-2、Un-3和Un-4以最小二乘法外推获得下一点迹数据。采用式（3）～（4）进行野值判定，假定测量数据的误差服从正态分布。

当获得的测量点数据Un满足：

计观测值估计误差为εn通常被称为新息，新息的统计特性与观测值的统计特性是一致的，根据上式可知其方差为

因此，对观测值Zn中是否有野值进行如下假设判断［5～7］：

εn满足可认为观测值中没有野值；

εn满足，可认为观测值含有野值； （6）

式（6）中，r是（M×1）维的向量（M为观测值的维数），其意义是表明工程上所能接受的极限误差，一般取4～6［8］。该判别方法的特点是简单易行，且物理意义明确，根据工程中的要求和环境的变化还可以随时调整r的分量。更为重要的是，通过该方法可清楚地判明观测值中的哪些分量超出了极限误差，从而可以有针对性地改进事先假定的目标运动状态模型、噪声统计特性等，达到提高滤波精度的目的。当新息εn超过给定的门限值时，观测值为野值，认为Zn不合理，此时调整增益Kgn，如式（7）：

其中，m∈［0，1］，类似于权系数。这样状态滤波方程式（6）将得到修正，既消除了野值点会使滤波发散的不利影响，又合理利用了野值中的有用信息。如果信息εn小于给定的门限值，则对增益Kgn不做改变［9～10］。

抗野值Kalman滤波可以克服初值是野值、间隔野值与连续野值的情况，但仍有个缺陷，当初值

D的选取准则根据测量设备的误差分布规律，参见［3～4］。

最小二乘法相比改进经纬度法，可以克服收到的第一个值是野值和野值间隔出现的情况，但仍有个缺陷，当野值连续出现3个以上时，算法会失效，无法滤掉野值。

2.3 抗野值Kalman滤波方法

是野值，则需经过多次递归调用才能收敛，实时跟踪到目标，且初值与真值差距越大，递归时间越长，不利于实时跟踪。

2.4 改进抗野值Kalman滤波

为了尽快跟踪，本文提出改进抗野值Kalman滤波，从两个方面进行改进。

第一，利用改进简单经纬度法确定第一个真值，然后调用抗野值Kalman滤波方法。

第二，式（7）的卡尔曼增益调整存在缺陷，若系统状态空间有多个变量，通过式（6）虽可清楚地判明观测值中的哪些分量超出了极限误差，但式（7）却对所有变量进行了修正，导致正确的值矫枉过正，降低滤波精度。因此，本文只对不合理值进行修正。

改进抗野值Kalman滤波可以克服连续野值，但参数设置较繁琐，不同的设备需要根据性能进行不断调整，以达到最优滤波效果。

3 实验结果和分析

经试验，雷神二次雷达测量序列中的野值较多，选应答码为6206的飞行数据检测分析；

如图2为原始数据在Matlab中的点图，飞行表现为：飞行器本应在“1”的航迹上，却不时跳到“2”的航迹，且并不是连续出现。

图2 原始数据Matlab点图

根据该设备测量性能，设置改进简单经纬度法滤波阈值为：DFilter=WDFilter=0.06。结果如图3，由于收到的第一个值不是野值，且野值不是间隔出现的，算法成功地滤掉了野值。

据设备的误差分布规律，在最小二乘法中设置D=0.6，结果如图4，没有连续3个以上的野值，所以算法成功地滤掉野值，且用推算出的真值代替野值，所以图4中的点比图3更加密集。

应用抗野值卡尔曼滤波方法，即初值不是测量真值，为野值。据某二次雷达测量性能，设置Q=［0.006；0.006］，R=［0.002；0.002］，r=4，W（1）=［0.011；0.001］，x（：，1）=［109.99 32.95］，A=［1 0；0 1］，m=0.002，p（：，1）=［0.01；0.01］。结果如图5，成功滤除野值，但需要循环递推几个点后方能找到真实航迹点，且初始值与真值差距越大，递推点数越多，收敛时间越长。该算法也利用推算出的真值代替野值。

图3 改进简单经纬度法Matlab点图

图4 最小二乘法滤波Matlab点图

图5 初始值非测量真值的抗野值Kalman滤波Matlab图

应用改进抗野值卡尔曼滤波方法，设置JDFilter=WDFilter=0.06，x（：，1）为改进简单经纬度找到的真值：x（：，1）=［110.712；33.917］，其余参数同上，结果如图6，不仅成功滤除野值，且能够快速跟踪到目标，提高了实时跟踪效率，为指挥员实时掌握飞行目标状态。

应用最小二乘法，人为加入3个连续野值后如图7，算法会失效，无法滤除野值；应用改进抗野值卡尔曼滤波方法，人为加入6个连续野值后，结果如图8，该算法可以克服最小二乘法的不足。

图6 改进改进抗野值kalman滤波matlab点图

图7 最小二乘滤波加入连续野值图

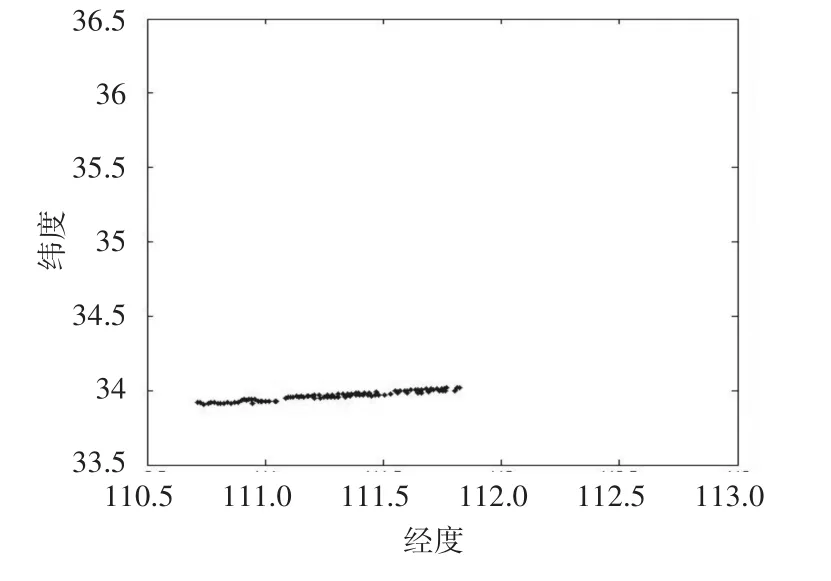
图8 改进抗野值Kalman滤波加入连续野值图

由上可知，各算法对不同野值的滤除效果不同，各有优缺点。改进简单经纬度法虽较大程度地保证第一个点为合法值，但遇到野点间隔出现的情况时，该算法会将合法值也滤除；最小二乘法可以较大程度克服改进简单经纬度法的弊端，但遇到连续3个以上野值也会将野值误认为合法值；抗野值Kalman滤波算法可以克服初值为野值与连续野值，但需要经过多次递归方能收敛，而改进抗野值Kalman滤波算法能够在连续野值出现时保持滤波的无偏性和稳定性，且能快速收敛跟踪，但该算法需根据不同设备设置不同的参数，较前几者计算较繁琐。

4 结语

在实际的工程测量中，观测值中出现野值的现象是经常发生的。针对雷达实时数据处理，本文总结、提出的野值判别与处理方法抗野值Kalman滤波不仅可以有效地识别野值，提高数据质量，消除野值对航迹显示的不利影响，可以应用在实时航迹数据处理等领域。

［1］胡绍林，孙国基.靶场外侧数据野值的统计诊断技术［J］.宇航学报，1999，20（2）：68-73.HU Shaolin，SUN Guoji.Range of the lateral statistical data outliers diagnostics［J］.Journal of aerospace，1999，20（2）：68-73.

［2］Jo-Anne T，Evangelos T，Stefan S.A Kalman filter for robust outlier detection［C］//Proceedings of the 2007 IEEE，2007，52：1514-1519 o-Anne T，Evangelos T，Stefan S.卡尔曼滤波器用于鲁棒异常检测［C］//Proceedings of the 2007 IEEE，2007，52：1514-1519.

［3］张世英，刘智敏.测量实践的数据处理［M］.北京：科学出版社，1977.ZHANG Shiying，LIU Zhimin.Data processing of measurement practice［M］.Beijing：Science Press，1977.

［4］贾浩正.抗野值的航迹数据Kalman滤波［J］.测控技术，2014，33（9）：26-28.JIA Haozheng.Outlier-proof track data Kalman filter［J］.Measurement and Control Technology，2014，33（9）：26-28.

［5］张怡，廉晶晶，黄文刚.抗野值性能的无迹卡尔曼滤波算法的研究［J］.计算机工程与应用，2012（33）：153-156.ZHANG Yi，LIAN Yi，HUANG Wengang.Research on the performance of the anti-wild value of karman filter［J］.Computer engineering and applications，2012，4（33）：153-156.

［6］张孝芳.基于M估计的抗野值卡尔曼滤波方法［J］.信息与电子工程，2005，3（2）：114-117.ZHANG Xiaofang.The anti-wild value kalman filtering method based on M estimation［J］.Information and electronic engineering，2005，3（2）：114-117.

［7］刘哲，王俊锋，武昱二，等.基于M估计的Kalman滤波野值方法［C］//第二十二届中国控制会议，2013，9（11）：4652-4655.LIU Zhe，WANG Junfeng，WU Yu，et al.Based on M estimation of Kalman filter field value method［C］//China con-trol conference of the 22nd session of China，2013，9（11）：4652-4655.

［8］吴建业，郑建辉，丁军辉.靶场测量中野值的判别与剔除方法研究［J］.战术导弹技术，2011（2）：98-100.WU Jiye，ZHENG Jianhui，DING Junhui.The detection and elimination of field values in the range of the target field［J］.Tactical missile technology，2011（2）：98-100.

［9］祝转民，秋宏兴，李济深.动态测量数据野值的辨识与剔除［J］.系统工程与电子技术，2014，8（14）：147-149.ZHU Zhuanmin，QIU Hongxing，LI Jishen.The identification and elimination of dynamic measurement data field values［J］.Systems engineering and electronics，2014，5（14）：37-40.

［10］金学军.基于最小二乘拟合的外弹道测量数据野值剔除方法［J］.四川兵工学报，2015，32（1）：22-26.JIN Xuejun.Based on the least squares fit，the field values of the field were eliminated［J］.Journal of military engineering in sichuan，2010，32（1）：26-26.