防空武器协同交战误差分析与建模仿真研究∗
2018-05-29严永锋
严永锋
(中国电子科技集团公司第二十研究所 西安 710068)
1 引言
现代空防作战中,隐身飞机、电子干扰、巡航导弹、反辐射导弹、弹道导弹、临近空间武器等成为防空武器系统的主要作战对象,作战过程中面临多种目标全空域饱和攻击、低空、超低空高速目标突防、反射击机动等威胁,传统的以单个火力单元为主的作战运用模式,各武器资源间存在着固定的隶属绑定关系,不同火力单元间的作战装备不能进行互操作,严重制约了武器系统作战效能的发挥,已不能适应现代空防作战要求,必须打破这种模式,将分散的传感器、指控和武器等各类作战要素进行横向组网、战术信息在各作战环节纵向贯通,通过防空作战体系内各作战要素间的信息共享和资源协同管控,形成网络瞄准、隐蔽抗击、交叉定位、异地制导、接力制导等网络化火力协同交战能力,弥补单个防空武器平台由于位置、环境或本身传感器和武器性能所带来的局限性,从而充分发挥各作战要素的效能,增强系统的快速反应、及时发现、稳定跟踪、协同交战存等能力,提升基于网络信息体系的一体化联合防空作战能力[1~2]。
2 需求分析
2.1 能力需求
1)灵活组网、机动部署,增强快速反应能力
利用无线、有线传输网络建立无中心、自适应传输网络,将战场空间内作战平台、作战要素或作战实体有效链接,融为一个有机整体,实现各作战单元的机动部署、无缝链接、灵活组网、可靠传输。
2)信息共享、稳定跟踪,改善跟踪态势质量
通过战术网络在各作战单元间共享各类战术信息,实现信息的获取、分发、处理、控制自动化,形成精确、连续、稳定复合航迹,共享单一集成态势(SIP),为多火力单元协同交战提供信息保障。
3)协同管控、信火一体,提升作战效能发挥
基于统一态势,按照相关准则,协同调度与管控作战兵力和要素,形成辅助决策预案,将信息优势转换为决策优势和作战优势,实现信息保障、火力优化、精确打击,形成“从传感器到射手”的最短杀伤链[3~4]。
2.2 对信息传输处理的要求
1)高精度
战术作战编成遂行防空反导作战任务时,组网后各火力单元共享搜索数据、跟踪数据、相对定位数据、导航数据以及授时信息等,对其采用预处理、质量估计、航迹优选、点迹相关、曲线拟合、角度配准以及动态加权等技术处理,获得准确的航迹信息,满足各制导平台火控级打击精度的要求[5]。
2)强实时
网络中各成员数据融合后的数据是提供给制导平台射击使用的,实时性要求较高,否则就会贻误战机。各平台同步周期为几十毫秒,数据处理需要在一个周期内完成。在信号检测、相关、数据融合算法及滤波方法的选择上,应选用快速有效的方法以实现实时运算。并需要通信系统提供快速通道,简化数据格式,完成多成员探测的目标解算,产生实时的目标航迹。
3)高可靠
未来防御作战,威胁目标速度更快、机动性更强,在对低空、超视距及电子干扰条件下的反隐身、反辐射目标跟踪时,受单个传感器视距探测、强电磁干扰及恶劣气象条件影响,单平台难以形成稳定、连续目标航迹,要实施武器打击,必须提供高可靠、满足武器打击质量的目标航迹信息。
3 误差精度分析
随着新一代超音速、末端高机动导弹的发展及使用,现役近程防御系统已难以满足作战需求,其效能将大幅度降低。下面从系统反应时间和处理精度等影响系统误差精度的因素进行分析。
3.1 精度分析理论
精度分析也称误差分析[6]。大型复杂系统有若干误差源,它们引起的误差可分为动态误差(滞后产生)、随机误差和系统误差三类,也可看成可预测性、不可预测性误差二类。
对动态误差,一般可采用线性相加法合成:
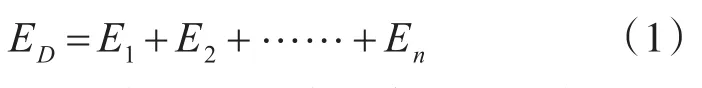
对系统误差,一般可采用带正负号的迭加法进行合成:
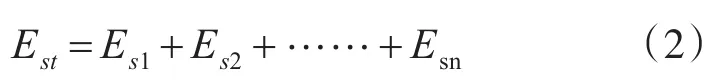
对随机误差,若满足独立条件,则采用均方根方法合成
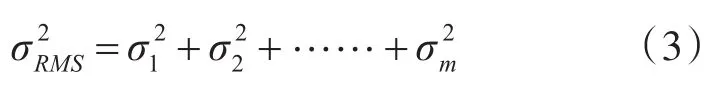
总系统误差:

其中,前两种误差可看成是随机误差的均值。对动态误差和系统误差,可采用测量-校正或补偿的方法减少,而随机误差通过滤波予以消除。
3.2 误差源分析
防空武器组网作战中制导雷达对目标和导弹的位置一般采用相对坐标系来测量和制导,误差源主要包括:制导雷达探测误差、基线转换误差、基线北向误差、空间传输误差、定位误差以及数据处理误差等。
在跨火力单元交战中引入的误差主要有三个环节:
1)将雷达探测到目标和导弹的相对坐标系的数据转换到本作战单元的绝对坐标系;
2)雷达探测的数据在分发共享中因误码率、丢包率、系统时延(包括传输、处理)等,对时空统一转换的影响;
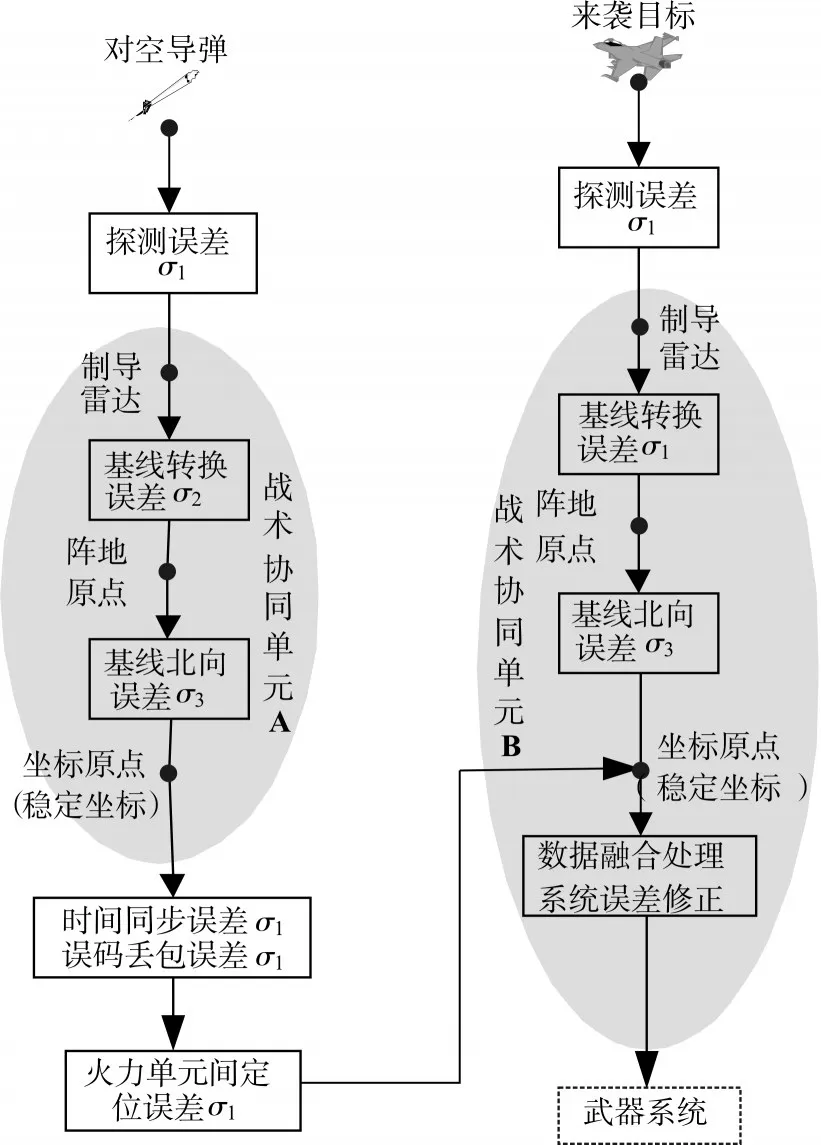
图1 系统误差源传递模型图
3)火力协同数据处理中系统模型原理性缺陷误差、关联误差、坐标变换误差、外推误差等。
对网络化信息系统来说,许多误差互相耦合、级联或并联,其关系非常复杂。在实际中,主要考虑较大的误差源。
系统误差源传递模型如图1所示:
1)制导雷达探测误差
制导雷达探测包括系统误差,随机误差,记为Δr0(距离),Δβ0(方位角),Δε0(俯仰角);对恒定的系统误差可采用事先标定方法进行修正,对于缓变的系统误差可采用共视目标实时动态估计方法进行修正;随机误差主要表现于雷达的量测噪声。主要方法是采用滤波器进行消除。
2)网络传输分发误差
系统时延主要包括数据预处理时延、空间传输时延、跟踪处理时延、火控解算时延等,火控级协同信息的系统时延一般在数十毫秒级,以3马赫的来袭目标为例,系统时延引起目标的位置预测误差可近似估算为σ=vmax*Δt≈36m,该量级的误差在火控数据处理算法的容许范围之内。
3)融合处理转换误差
武器系统组网作战制导雷达对目标和导弹的位置一般采用相对坐标系来测量和制导。在组网条件下,首先将各制导雷达站测量的球面坐标转换为平台的直角坐标,然后将其转换为协同处理站的直角坐标,经协同处理站进行融合、外推处理后,送至武器系统坐标系[8~9]。
(1)相对坐标转换
目标T在A点的当地极坐标系中的坐标(ra,εa,βa),以及 A 点与 B 点相互观测的极坐标(r,εab,βab)和(r,εba,βba),可按下面的模型解算出目标 T 在 B 点的当地极坐标系中的坐标(rb,εb,βb)。
①A点的当地极坐标系中的仰角补偿
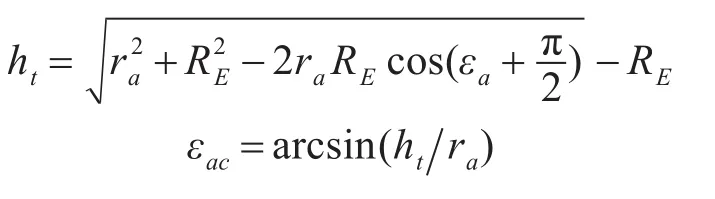
②目标T由A点的当地极坐标转换到B点的当地极坐标
由于A点与B点较近(相对距目标而言)且高度相同,可假定εab=εba=0,根据余弦定理,两点至目标在地面的投影点的距离(或近似看为两斜距在水平面的投影)为
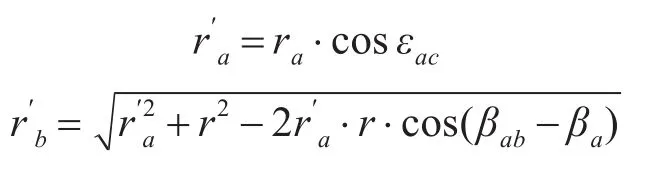
最终,根据以上各值得到转换到B点的T坐标为
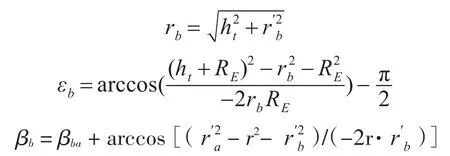
(2)误差估计
在不考虑测量的随机误差,只有系统偏差时,k时刻2个传感器分别在各自极坐标系中对目标的测量向量表示为
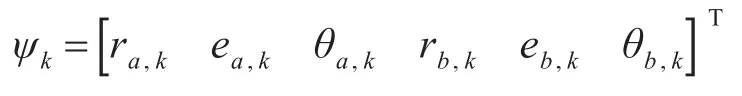
对目标的测量向量的系统偏差表示为
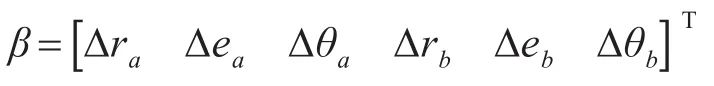
转换到当地不稳定东北天直角坐标系,可以得到:
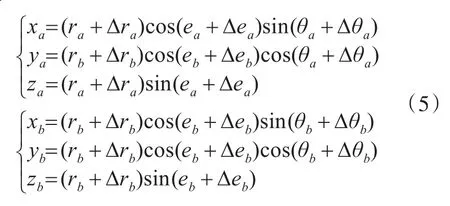
令
当两个传感器的地理位置分别为(La,λa,Ha)和(Lb,λb,Hb),摇摆角分别为(ωa,φa,θa)和(ωb,φb,θb)时(其中ω为航向角,θ为横摇角,φ为纵摇角),目标转换到地心(ECEF)直角坐标时如下式表示:
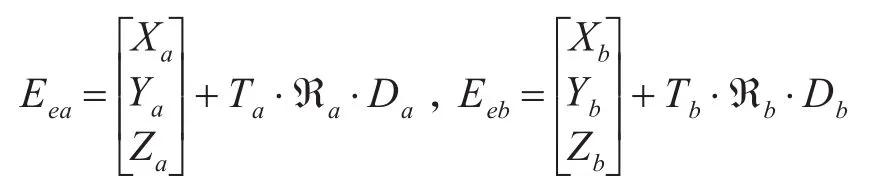
其中
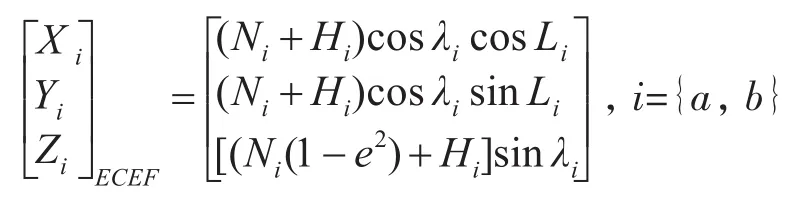
式中Ni为椭球卯酉圈曲率半径,为第一偏心率,R为椭球长半径,r为椭球短半径。
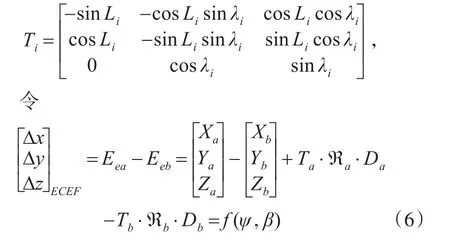
对(6)式一阶泰劳展开,并假设(β-β′)和(ψ-ψ′)足够小且高阶分量可以忽略,则有:
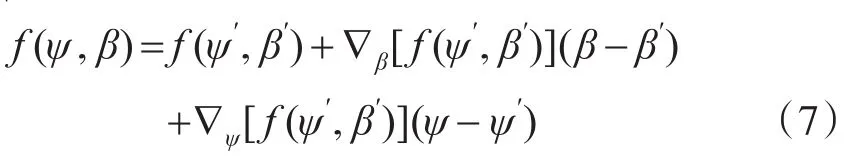
其中表示k时刻传感器的真实测量值,β′表示对系统误差的初始估计。式(7)中:
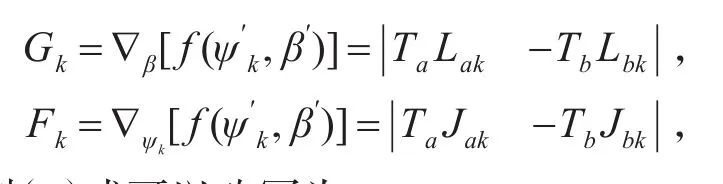
则(7)式可以改写为
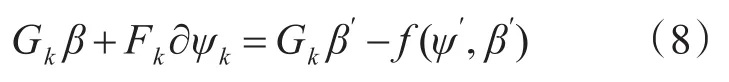
令,则有:

前N个时刻的测量值可以表示为

其 中据此可以用广义最小二乘法求解得估计值:
最后,用对传感器1和传感器2的目标探测值进行修正,完成传感器的配准和数据转换前的修正。
3)误差修正
依据导弹数据对转换后的目标数据进行误差修正,主要目的是为保证转换后的目标与导弹之间的偏差其精度应该不低于转换前精度。主要手段为通过两平台同时对导弹的观测值获得导弹的转换偏差,来修正转换后的目标数据,从而达到保证弹目偏差精度的目的。
4 仿真分析
4.1 场景设计
在实际仿真实验中,飞机速度为3马赫,高度保持8000m,选取1个战术级指挥所和2个战术单元,其中战术单元沿敌机来袭方向部署在战术级指挥所前方,通过战术数据链,实现战术指挥与火力单元制导信息的共享,进行火控级跟踪精度分析。
4.2 误差模型
将节点1、节点2、节点3探测到的雷达点迹进行融合处理,假设雷达同时开机,雷达处于精跟状态,雷达的测量误差包含随机误差和固定误差两部分,其中测距随机误差为0.9Δr,固定误差为方位角、俯仰角随机误差为 0.8Δθ,固定误差为
4.3 仿真结果
1)节点1单雷达与复合航迹对比
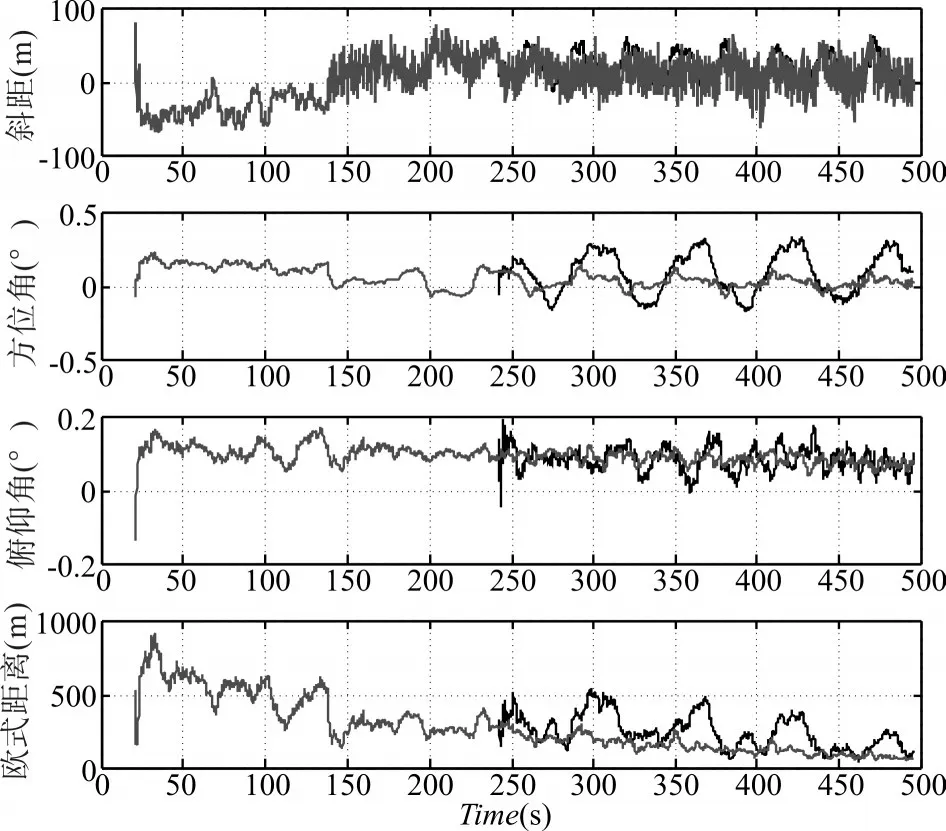
图2 精度误差分布图
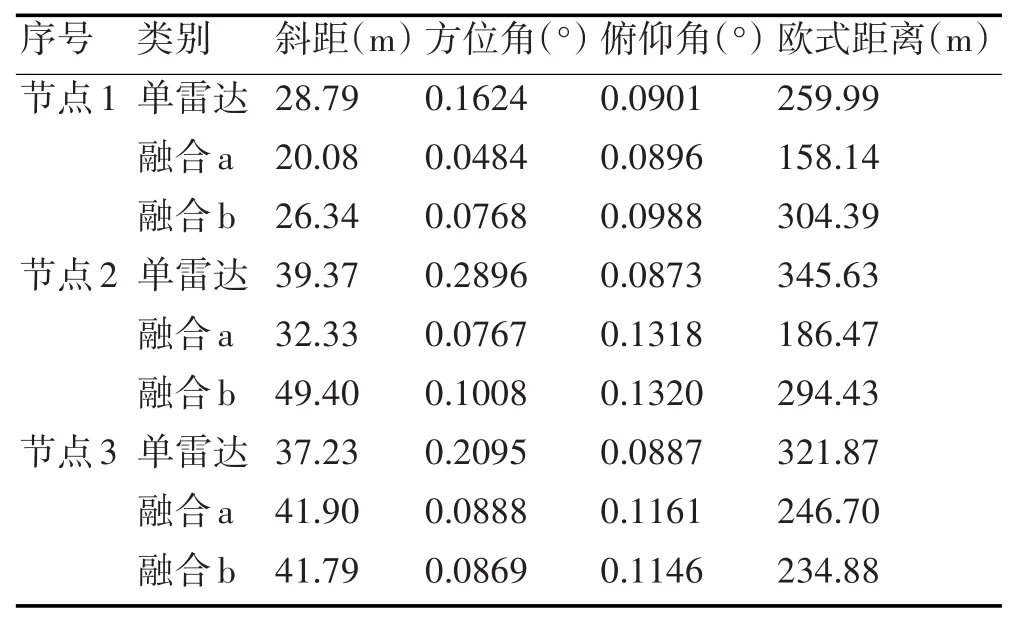
2)航迹误差统计结果
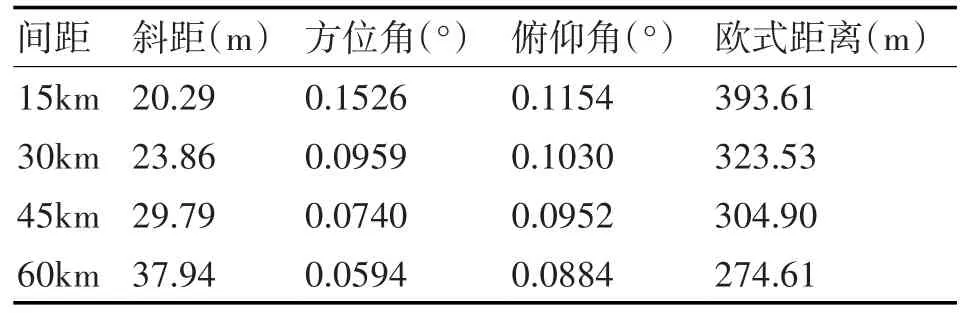
3)战术单元部署位置对融合精度的影响
4.4 小结分析
1)对高速高机动目标跟踪时,跟踪精度有所下降,但航迹精度明显高于单雷达跟踪质量。
2)在多雷达组网使用时,需要适当拉开各雷达间的水平距离(如40km~60km),尽可能增大各雷达之间的高度差,以获得良好的融合效果。
5 结语
高机动、反隐身反辐射空战武器的迅速发展,对现代防空反导作战提出了新的需求,本文从作战样式分析入手,研究了跨平台协同交战中武器系统作战过程中主要影响因素,分析了作战过程各环节误差源,建立误差传递数学模型,基于误差理论推导了制导雷达对准理论真值的最大绝对误差计算公式,并结合典型作战场景进行了仿真分析,为武器跨平台协同交战的的后续发展提供技术参考。
参考文献
[1]孙连山,杨晋辉.导弹防御系统[M].北京:航空工业出版社,2005.
[2]陈立新.防空导弹网络化体系效能评估[M].北京:国防工业出版社,2007.
[3][美]Peter J.Mantle.导弹防御方程式[M].薛维民,张耀程译.北京:空军装备研究院地面防空装备研究所,2004
[4]宋跃进,秦继荣.指挥控制与活力控制一体化[M].北京:国防工业出版社,2008.
[5]王小非.C3I系统中的数据融合技术[M].黑龙江:哈尔滨工业大学出版社,2012.
[6]何友,王国宏,彭应宁.多传感器信息融合及应用[M].北京:电子工业出版社,2010.
[7]Zhou Y F ,Henry L,Martin B.Sensor alignment with Earth-centered Earth-fixed(ECEF) coordinate system[J].IEEE Transaction on Aerospace and Electronic Sys⁃tem,1999,35(2):410-418.
[8]董云龙,何友,王国宏.基于ECEF的广义最小二乘误差配准技术[J].航空学报,2006,27(7):463-467.
[9]赵杰,江晶等.基于地心地固坐标系的多传感器实时配准方法[J].空军雷达学院学报,2008,22(6):79-82.
[10]聂永芳,冯林平,施建礼.新误差分析方法对反舰导弹作战使用的影响[J].舰船电子工程,2012,32(7):57-58.
[11]曹林平,黄长强.武装直升机无控武器射击误差源分析[J].火力与指挥控制,2000,25(1):70-73.
[12]倪天权,王春波,张殿友.两舰协同定位误差分析的研究[J].江苏科技大学学报(自然科学版),2008,22(2):11-14.
[13]施荣,陈兢,辜璐.美国一体化防空反导系统作战能力分析[J].航天电子对抗,2008,24(2):1-4.
