基于支持向量机的超声强化加工表面性能预测

陈 爽， 胡家进， 赵录冬

(江西理工大学 机电工程学院, 江西 赣州 341000)

超声振动挤压强化技术广泛地应用在表面加工领域[1]，其加工机理是通过高频振动的硬质滚轮作用于待加工金属表面，使工件表面的微观波峰波谷被压平，表层金属产生塑性变形及残余压应力，并且在此过程中还产生了冷作硬化，达到改善金属表面质量的目的。与传统的磨削抛光技术相比，超声强化加工既能提高其表面硬度，又降低其表面粗糙度，同时还可弥补微裂纹的缺陷[2]。

多数关于表面振动挤压强化的研究都是对加工后的表面性能进行研究，而对于不同工艺参数下的零件表面性能的变化情况和预测研究较少[3-7]。本文在对45号钢进行超声强化实验研究的基础上，设定不同超声强化工艺参数，可得到一系列的表面粗糙度值和硬度值;再通过支持向量机理论进行分析，建立了支持向量回归(SVR)预测模型，对其强化后的表面性能进行预测，最终得到性能的变化规律和最优参数值。

1 支持向量机非线性迟滞模型原理

1.1 支持向量机的回归原理(SVR)

对于复杂的模型结构，在解决样本信息有限的情况下，支持向量机具有独特的优势。为了对实验数据进行有效分类，在SVR中首先建立一个最优判定超平面，之后让其两侧到该平面最近的两类样本之间的距离最大化。支持向量机解决非线性问题的基本思路是：通过核函数将低维空间的训练样本转化到高维空间中去，再利用高维空间得到的线性分类面构造支持向量机的回归函数，进而对低维空间的训练样本进行预测。

对于训练样本(x1,y1),(x2,y2),…,(xn,yn),其回归函数为

f(x)=ω·φ(x)+b。

(1)

式中：ω为超平面系数矩阵，x为输入向量，b为待定偏置量，φ为未知的高维函数，ω·φ(x)表示ω与φ(x)的内积，f(x)为输出变量。本文f(x)为粗糙度或硬度，其中x为速度与挤压组成的向量，或者挤压力与挤压次数组成的向量。

(2)

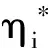
(3)

其中：R(zi,zk)表示核函数，R(xi,xk)=φ(xi)·φ(xk)，即为φ(xi)与φ(xk)的内积[10]。取R(x,xi)=exp(-g‖x-xi‖2)，其中g为核函数的宽度参数。

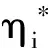
(4)

偏置量b采用Karush-Kuhn-Tucker条件得到

(5)

结合式(1)、(4)和(5)，得到最终的回归函数，其表达式为

f(x)=ω·φ(x)+b=

(6)

1.2 惩罚参数c和核函数宽度参数g优化

考虑到回归函数中的惩罚参数c与核函数宽度参数g对其建立的准确性有重要影响,其中g与训练样本点的数量成正比。由于参数c的取值影响回归函数的复杂程度，故通过对该系数进行优化，可以使回归函数泛化能力与拟合精度达到平衡。参数c和g的取值需依据实际测量值来进行分析筛选。

本文采用栅格化搜索的方式对(c,g)进行寻优，能高效地在规定范围内得到最优值。但由于系统误差的存在，(c,g)的寻优结果会受到粗糙度和硬度数据的影响，为此利用交叉验证法对每组(c,g)寻优，可使其回归函数不受实验误差的影响。

参数(c,g)组合寻优流程如图1所示。步骤说明如下。

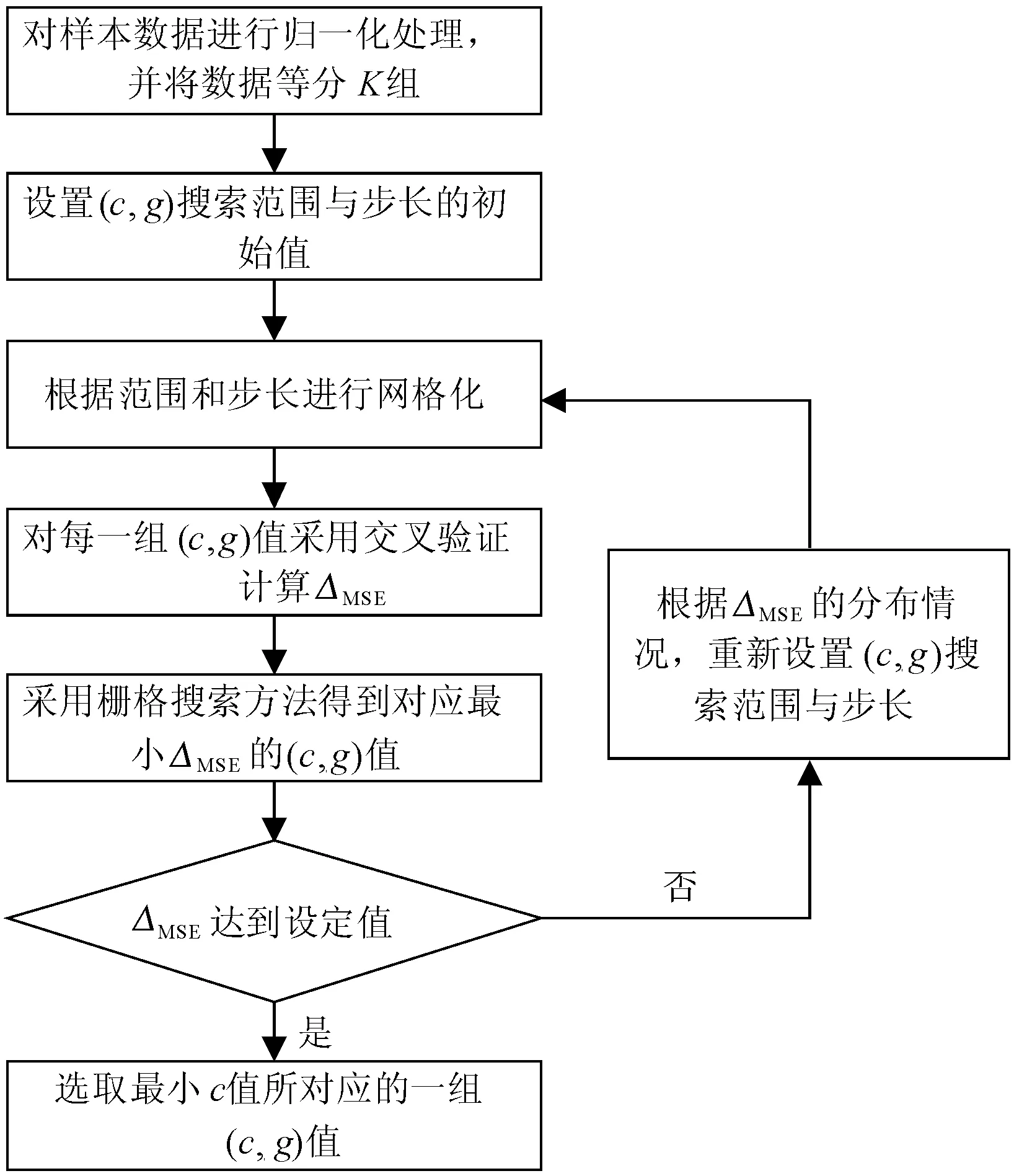
图1 参数(c,g)的寻优流程Fig.1 Parameters (c, g) of the optimization process

步骤1:由于需要缩小训练样本带来的误差，需要对其样本进行归一化处理，表达式为

(7)

步骤2:采用对数形式对步长进行设定，估测(c,g)的取值范围。

步骤3:设定均方误差MSE，计算公式为

(8)

式中，f(xi)为回归函数的预测值，yi为训练样本点。

步骤4:重复步骤3，计算N组均方误差MSE值，并且得出N组MSE的均值ΔMSE,其中ΔMSE为回归函数在(c,g)下的误差。

步骤5:改变(c,g)组合值，重复步骤3和4，计算出其范围内所有(c,g)组合值对应的均值ΔMSE。

步骤6:设定均值ΔMSE的最小值，再对其进行对比，若均值ΔMSE小于设定值，则该组(c,g)值即为最优值，并且搜索停止。若均值ΔMSE大于设定值，则需要判定对其搜索范围是扩大还是缩小。继续重复上述步骤3至5，直到所得结果小于最小均值ΔMSE为止。

2 实验验证

2.1 实验数据测定

实验装置如图2所示。根据超声振动挤压强化的机理研究，本实验将机床主轴转速、工具头的进给速度、振幅、挤压力和挤压次数视为影响超声强化加工的主要工艺调整参数，对于工具头的半径和振动频率则保持恒定不变。

图2 超声振动挤压加工设备图Fig.2 Ultrasonic vibration extrusion equipment

由于实验影响因素较多，传统的单因素试验方法不能考虑众多因素，故采用正交试验方法代替传统的方法。五因素四水平正交试验如表1所示。

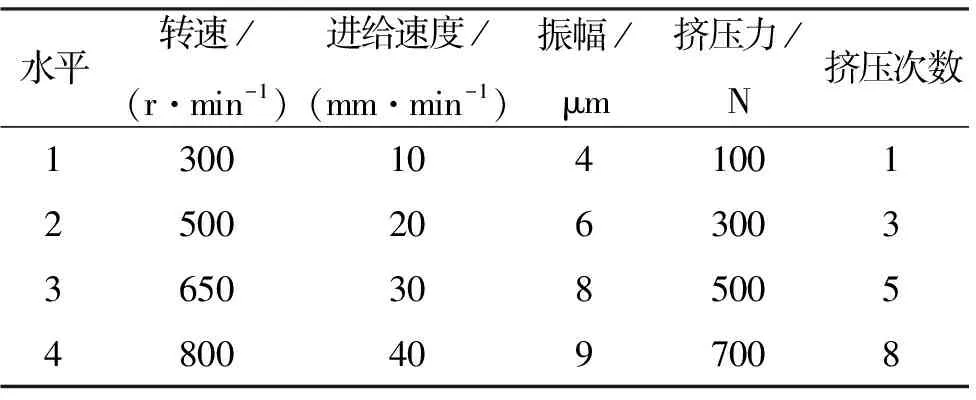
表1 超声振动挤压因素水平表Tab.1 Factors and levels of ultrasonic vibration extrusion

首先对45号钢的轴类零件进行精车，之后将超声振动挤压强化设备装夹到车床上，参照表1中的参数对零件进行强化实验。利用粗糙度检测设备和显微硬度计测量所有强化加工后的样本零件，每个样本零件需要进行3次测量，最后取其平均值。所得平均值即为该样本零件的表面粗糙度和表面显微硬度，结果如表2和表3所示。

表2 表面粗糙度实验结果Tab.2 Experimental results of surface roughness

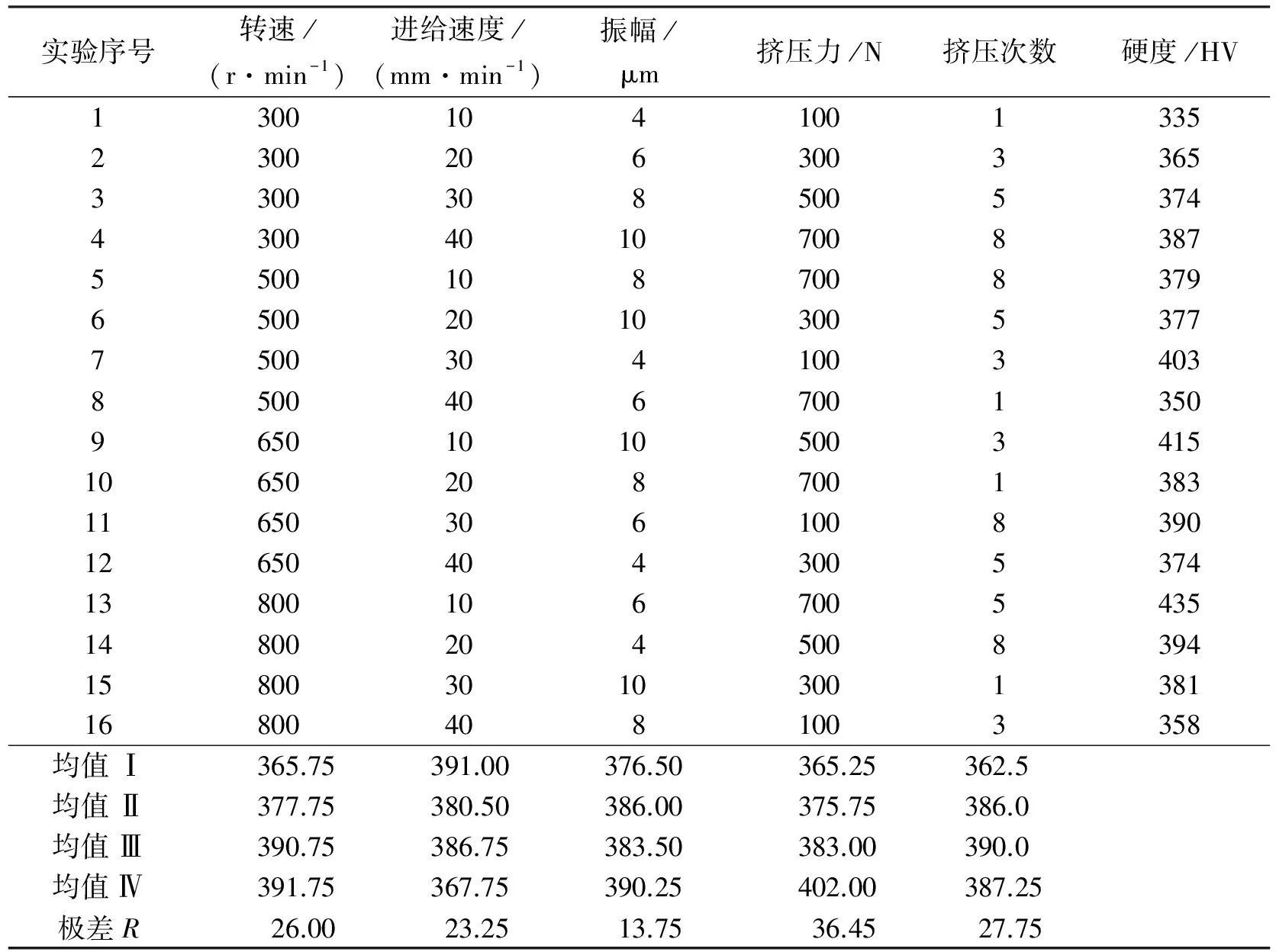
表3 表面显微硬度实验结果Tab.3 Experimental results of surface micro-hardness

对极差R分析可知，对零件表面粗糙度影响最大的因素是进给速度和挤压力，而对其影响相对较小的因素为主轴转速、振幅及挤压次数。因此,研究零件表面粗糙度的变化趋势，只需考虑进给速度和挤压力的变化，其他3个因素只需取各参数的最优值即可。对于表面粗糙度值的处理，可将测得的一系列样本零件的表面粗糙度值代入支持向量机非线性模型中求解，得出表面粗糙度预测模型的回归函数，进而通过回归函数计算任意点的表面粗糙度值。

零件显微硬度值的处理同样可采取上述方法，将挤压力和挤压次数设为可变参数，其他3个因素依然取各参数的最优值，运用支持向量机非线性模型来求出回归函数，再计算任意一点的表面硬度值。

通过正交试验可知，对于粗糙度，取500 r/min、8 μm和5次分别为主轴转速、振幅和挤压次数的最优参数组合；而对于硬度，取800 r/min、10 mm/min和10 μm分别为主轴转速、进给速度和振幅的最优参数组合。为了更准确地预测，将另外两个变量根据等差原则，在允许范围内取28组数据，将所测量的表面粗糙度值和硬度值都代入到支持向量机模型中，得到非线性模型和回归函数，之后预测在允许范围内的表面粗糙度和硬度值。

2.2 粗糙度参数(c,g)寻优

为得到拟合样本，实验测量样本数据点如表4和5所示。

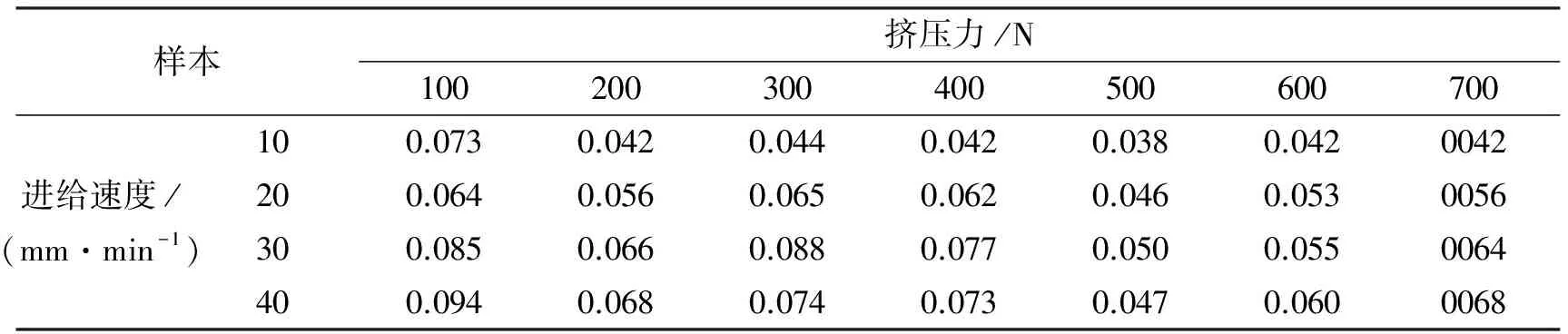
表4 粗糙度的样本数据点Tab.4 Sample data points of roughness μm

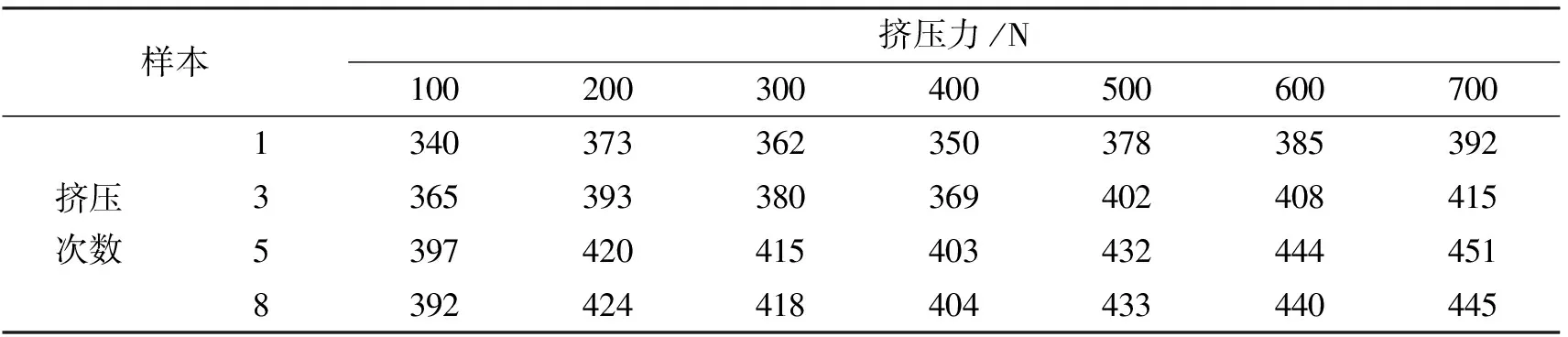
表5 硬度的样本数据点Tab.5 Sample data of hardness HV

通过表4和表5选取预测样本中粗糙度样本点分别为(10,100)、(20,200)、(30,300)、(40,400)、(30,500)、(20,600)、(10,700),硬度样本点分别为(1,100)、(3,200)、(5,300)、(8,400)、(5,500)、(3,600)、(1,700),其他值则为拟合样本。初始化中c和g的搜索范围为[2-5,25]，步长均为2-1,K=3,ε=0.001,Δmin=10-4,将训练样本代入式(6)中。图3和图4表示拟合过程中每组(c,g)对应的均值ΔMSE。由图3b和图4b可以看出均值ΔMSE的变化趋势，因此能够进一步得到最优(c,g)值组合。粗糙度对应的c=0.18,g=2.3,ΔMSE=4.26×10-4,硬度对应的c=1.4,g=0.03,ΔMSE=3.45×10-4。

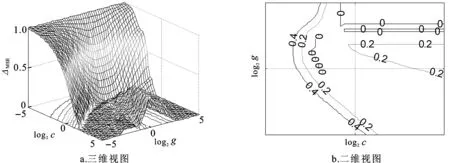
图3 粗糙度参数(c,g)的寻优图Fig.3 The optimization of roughness parameters (c, g)

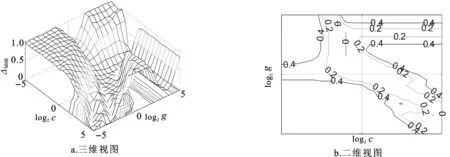
图4 硬度参数(c,g)的寻优图Fig.4 The optimization of hardness parameters (c, g)

3 预测结果求解及分析

依据上述实验结果，通过非线性迟滞预测模型对表4和表5中所有样本点进行求解，进而得出图5所示的回归曲面。

图6所示为回归函数的误差分布图，展示了粗糙度与硬度曲线拟合的准确性。通过将预测样本中的点分别代入曲线，计算出表面粗糙度和硬度值误差。图6a和图6b分别表示粗糙度回归函数和硬度回归函数的预测值与实际测量值之间的误差分布,由图中各点分布可得出其误差的取值范围是[-0.003,0.002]μm，表明支持向量机的函数回归模型能够准确地预测进给速度、挤压力与粗糙度，挤压次数、挤压力与硬度之间的关系。

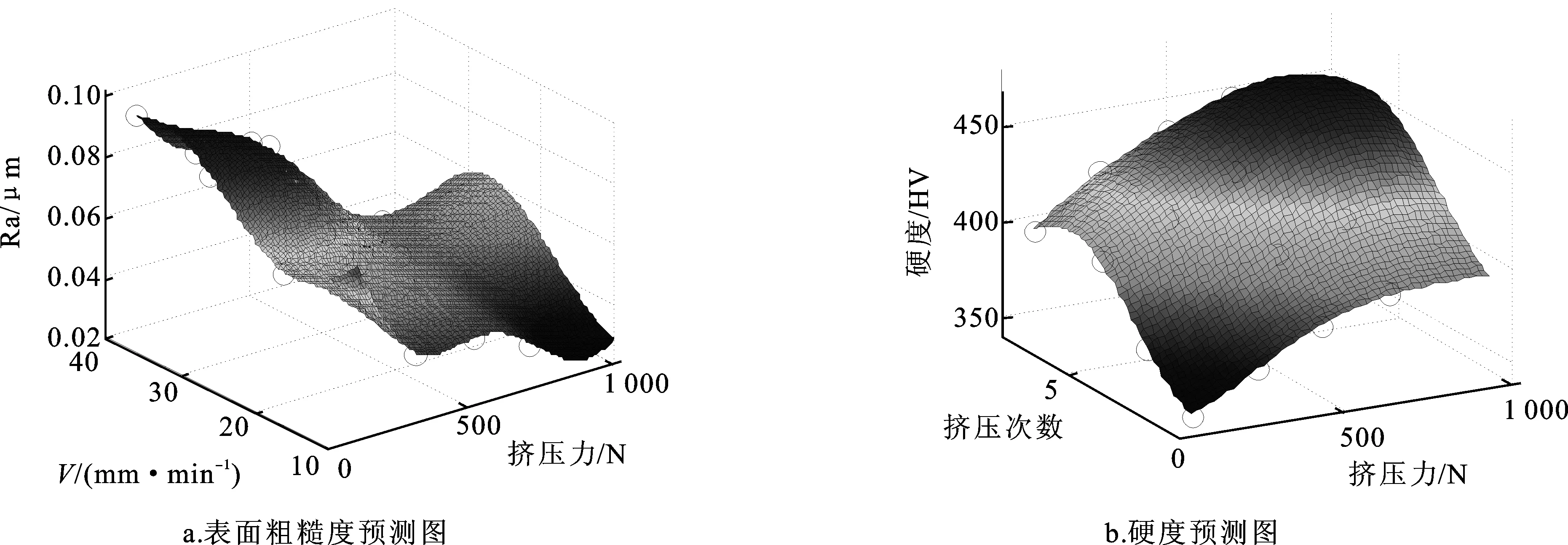
图5 预测结果图Fig.5 Prediction result

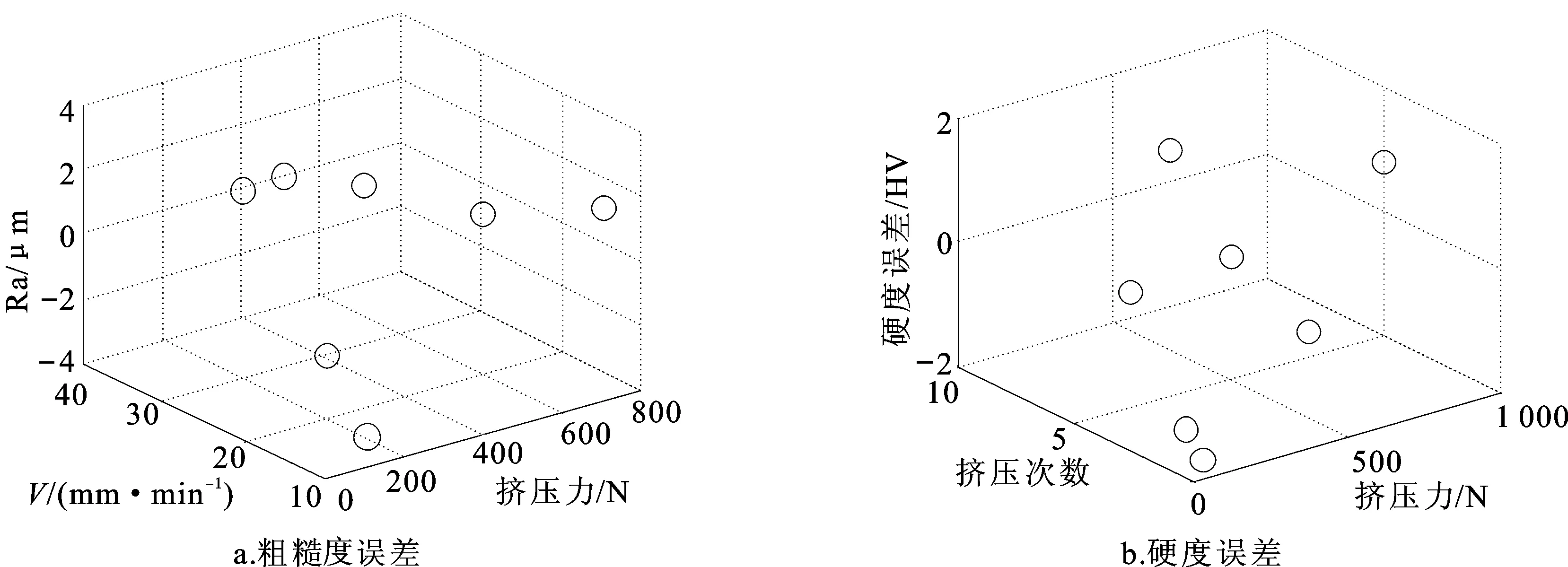
图6 误差分布图Fig.6 Error distribution of regression function

将预测值与实际测量值对比，结果如表6和表7所示。

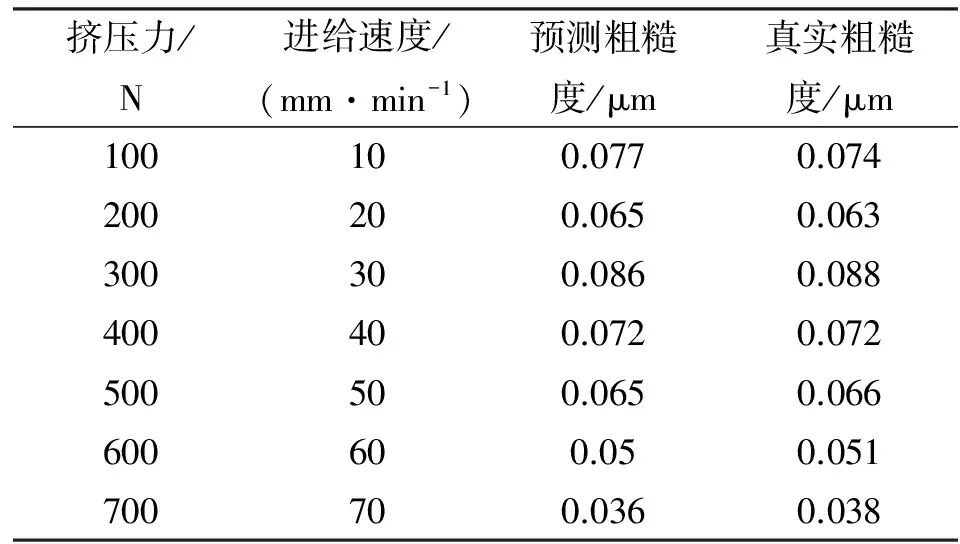
表6 粗糙度真实值与预测值对比Tab.6 Comparison of real value and forecast value of roughness

表7 硬度真实值与预测值对比Tab.7 Comparison of hardness True value and predictive value

由上述表6和表7分析可知，利用支持向量机非线性预测模型计算出表面粗糙度和硬度的回归函数，其预测值与实际值之间的误差范围落在允许值内，回归函数正确，并求得进给速度为10 mm/min、挤压力为927 N时表面粗糙度最小，其值为0.023 68 μm。表面硬度在挤压力为798 N、次数为6次时最小，其值为462.7 1HV。

4 结论

本文运用支持向量机理论，建立超声强化表面性能预测模型。利用核函数将低维空间的训练样本转化到高维空间中去，通过高维空间得到的线性分类面构造支持向量机的回归函数。此模型可以准确地获得在超声强化加工中进给速度、挤压力与粗糙度，挤压次数、挤压力与硬度之间的非线性特性。最后通过实验验证得出，此模型对于利用超声强化加工后零件的表面粗糙度和硬度的预测合理，可以准确地预测超声强化加工的表面粗糙度和硬度。

：

[1] 朱有利, 王燕礼, 边飞龙,等. 金属材料超声表面强化技术的研究与应用进展[J]. 机械工程学报, 2014,50(20):35-45.

[2] 曹凤国. 超声加工技术 [M].北京:化学工业出版社, 2005.

[3] ISHIKAWA K I, SUWABE H, NISHIDE T et al. A study on combined vibration drilling by ultrasonic and low-frequency vibrations for hard and brittle materials[J]. Precision Engineering, 1998, 22(4):196-205.

[4] 陈利钦, 项彬, 任学冲,等. 表面超声滚压处理工艺对高速列车车轴钢表面状态的影响[J]. 中国表面工程, 2014, 27(5):96-101.

[5] THOE T B, ASPINWALL D K, KILLEY N. Combined ultrasonic and electrical discharge machining of ceramic coated nickel alloy[J]. Journal of Materials Processing Technology, 1999, 92/93(9):323-328.

[6] 郑建新, 刘传绍, 蒋建军. 无磨料超声抛光工艺参数优选试验研究[J]. 制造技术与机床,2009(2):93-95.

[7] 王义,鲍绍箕.超声振动挤压强化工艺研究:强化方法及其工艺效果[J]. 电加工与模具,1991(3): 15-19.

[8] 王定成, 方廷健, 高理富,等. 支持向量机回归在线建模及应用[J]. 控制与决策, 2003,18(1):89-91.

[9] 包广清,郑文鹏. 基于正交设计和支持向量机的横磁通永磁电机参数优化[J]. 应用基础与工程科学学报,2012,20(5):912-921.

[10] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(3):123-124.

[11] SHEVADE S K, KEERTHI S S, BHATTACHARYYA C, et al. Improvements to the SMO algorithm for SVM regression[J]. IEEE Transactions on Neural Networks, 2000, 11(5):1188-1193.