高墩刚构桥悬臂施工稳定安全性评估

岐峰军,骆佐龙,姚远,檀妹静



高墩刚构桥悬臂施工稳定安全性评估

岐峰军1,骆佐龙2*,姚远3,檀妹静4

1. 长安大学公路学院, 陕西 西安 710064 2. 山西大学土木工程系, 山西 太原 030000 3. 中国建筑设计院有限公司, 北京 100044 4. 北京临近空间飞行器系统工程研究所, 北京 100076

鉴于当前研究和应用的局限，本文结合非线性有限元结果与逆可靠度方法提出可以考虑参数随机性的高墩刚构桥悬臂施工稳定安全性评估分析计算方法。通过非线性有限元获得结构稳定性荷载与抗力建立极限状态函数，进而应用逆可靠度数学模型求解。结果表明，该方法既能够考虑参数随机性，从而得到更加客观可靠的结果，又沿用了易于接受的传统方法的安全系数表达形式，具有良好的工程应用价值和实用意义。

刚构桥; 施工安全; 评估

连续刚构桥在最大悬臂施工阶段，连续体系尚未形成，结构体系稳定性最差，确保高墩刚构桥悬臂施工稳定至关重要。传统的验算方法基于确定性理论，简便实用但忽略了参数随机性[1-3]。参数随机性包括外部作用和内部抗力的随机性，这些随机性在施工过程中表现得更加明显却更加难以精确控制的同时，此时结构稳定储备余量更小。因此，采用确定性分析可能会导致施工阶段较小的安全余量不足以包络住参数的随机波动，导致悬臂施工阶段的失稳问题。因此，必须将可靠度理论引入高墩刚构桥悬臂施工稳定安全性评估。

规范涉及了倾覆稳定相关规定[4,5]。但是，相关规定没有细化到施工阶段或针对每种施工工法、没有充分考虑参数随机性，另外规范取值确定的理论依据也阐述得不够充分。另一方面，工程结构的分析和设计已经向着基于数理统计原理的可靠度方向发展，当前的实际工程实践应该向此靠拢。

目前，已有一些刚构桥施工稳定性的可靠度分析[6,7]，但表达形式偏于理论，尚不便于设计使用。而逆可靠度方法的提出和发展，可以基于可靠度理论反求指定表达量，为建立可靠度指标与稳定安全系数的直接映射关系提供了思路，也已有一些应用[8-10]。由上述分析可知，目前仍缺乏针对高墩刚构桥悬臂施工稳定安全性的客观可靠同时简便有效的分析方法。本文结合使用逆可靠度分析与非线性有限元结果，采用考虑随机性的安全系数来进行高墩刚构桥悬臂施工稳定安全性评估。

1 基础理论

1.1 可靠度反分析原理

本文方法是：建立可靠度反分析数学模型如下：

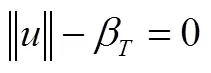
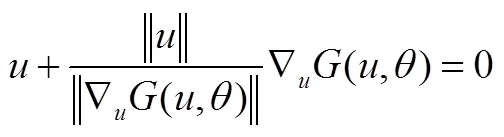
式中、和β分别为随机变量、待求量和目标可靠度指标。

依据β的几何意义，结合设计点法和线性Taylor展开，可以建立（设计点处表为0）与β的映射关系：

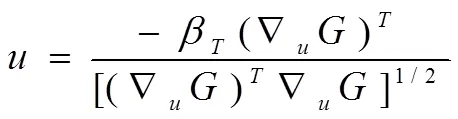
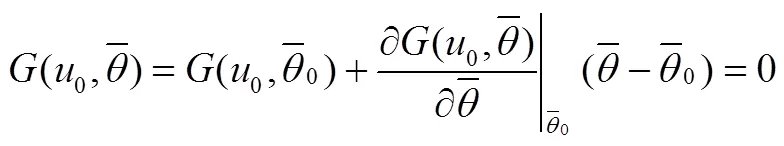
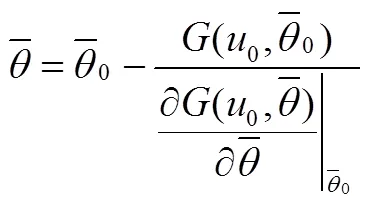
进行多次迭代，直到满足收敛条件时即求得待求量。以上为本文逆可靠度分析部分的核心算法。

1.2 分析流程

本文求解方案需要得到(,)=0，对于高墩刚构桥悬臂施工稳定极限状态，临界承载能力和外部作用可以由非线性有限元获得，从而获得上述反分析过程需要的(,)=0。据此，本文建立的分析流程如下所示：

图 1 稳定性评估流程

2 算例验证

以文献[11,12]算例验证，(,)=0具体形式为：=exp[-(1+22+33)]-4+1.5 (7)

其中：(1,2,3,4)~(0,1)，为确定性待求量，设β=2.0。求解过程见表1

表 1 迭代过程

可见，迭代很快收敛，且待求量求解结果与文献[11,12]结果基本精确一致。

3 实例分析

某铁路高墩刚构桥，跨径布置为(88+168+88)m，主梁、薄壁墩分别采用C50、C40混凝土。悬臂浇筑施工，最大悬臂状态为84 m，高墩104 m。单侧挂篮重量为1100 kN。

3.1 可靠度分析模型

根据研究，高墩刚构桥最大悬臂状态稳定分析极限状态方程可表示如下（表示待求解的稳定安全系数）：=-=kkR0-(kS+S) （8）

式中：k、k分别为高墩抗力计算模式、混凝土弹性模量的不定性系数；k为恒载不定性系数，以上三个不定性系数作为基本随机变量，分布如下：

表 2 参数特性

式（8）中，0表示确定性分析得到的稳定抗力，S为结构恒载的倾覆等效外力，S为挂篮荷载的倾覆等效外力，以上三项均由非线性有限元分析得到。

将以上相关数据及计算结果代入（8）式，得到本文实例用于分析的可靠度数学模型为：

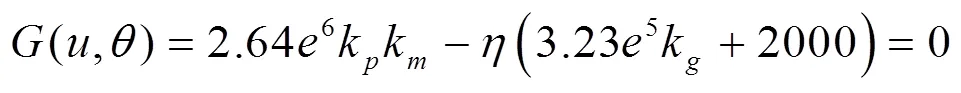
3.2 安全系数分析

高墩刚构桥悬臂施工稳定安全性评估以基于可靠度理论、考虑了参数随机性的安全系数形式表示。由于本文方法建立的是与β的关系，因此分析前需确定β取值。根据国外研究和相关规范，β基准值取为3.5。

与β对应计算如表3、图2。

表 3 安全系数计算结果

图 2 h与βT关系

根据表3和图2分析，与β呈负相关关系，且影响剧烈。另一方面，按照（9）式，若不考虑参数随机性，即确定性分析结果为7.8466，可见确定性分析忽略了随机性后大幅高估了高墩钢构的稳定性储备，若实际工程施工期稳定安全储备余量不足，将造成确定性分析无法捕捉到结构的失稳风险。

3.3 参数敏感性分析

求解结果如图3、图4和表4。

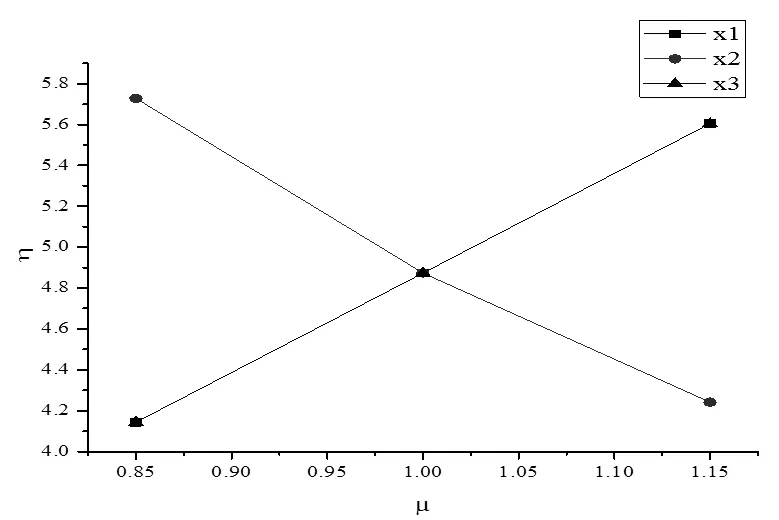
图 3 h与µ关系

图 4 h与s关系

表 4 不同参数分布类型安全系数计算结果

根据图3、图4和表4分析可知，随机变量统计参数对求解结果影响明显。由于极限状态函数的特殊形式，k与k是乘积形式，故两者变化曲线相同，而曲线则有所差异。分析表明，k对影响最为明显。此外，参数分布类型也有一定影响。

3.4 迭代初值h0影响

分析不同0影响，如图5。根据图5，本文提出的算法稳定高效，结果对初值不敏感。

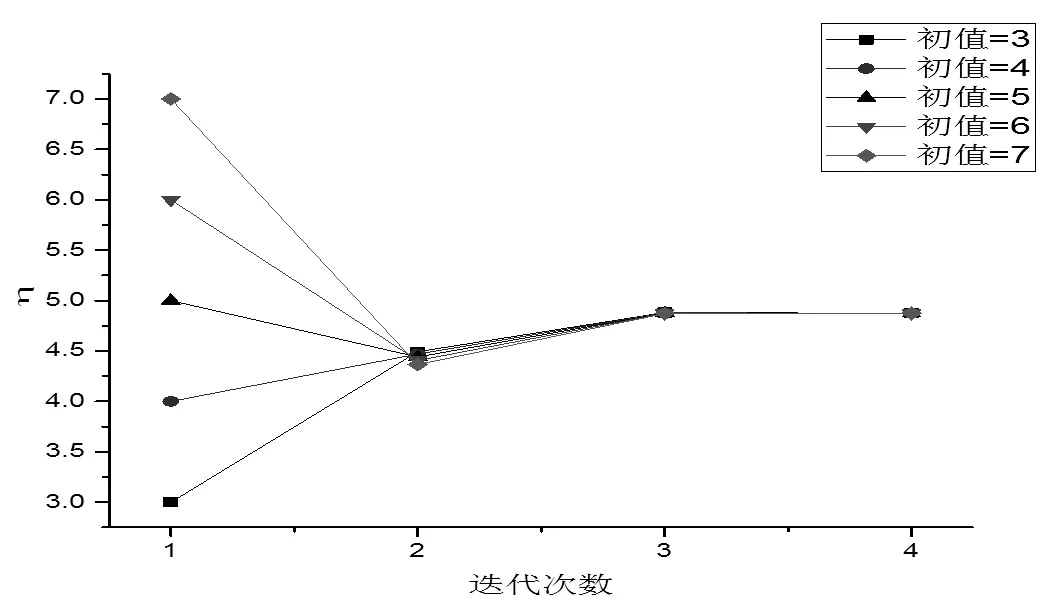
图 5 h与h0关系

4 结论

结合非线性有限元结果与逆可靠度方法提出可以考虑参数随机性又简便实用的高墩刚构桥悬臂施工稳定安全性评估分析计算方法。研究表明：可靠度分析将弥补确定性分析可能消耗掉施工期间不宽裕的安全储备这一缺陷从而确保高墩刚构桥施工安全。与β呈现明显的负相关关系，且对于参数的统计特性和分布类型比较敏感，在可靠度分析中对于参数统计特性的取值是至关重要的基础工作。本文算法稳定可靠，简便易用，具有良好的工程实用意义。

[1] 赵伟封,马保林,陈偕民,等.薄壁特高墩预应力混凝土连续刚构桥的空间稳定性[J].长安大学学报:自然科学 版,2004,24(4):51-54

[2] 王菲,田山坡,禚一.高墩大跨连续刚构桥的稳定性分析[J].铁道工程学报,2012(10):57-62

[3] 吕毅刚,余钱华,张建仁.能量法分析高墩大跨连续刚构桥稳定性[J].长沙理工大学学报:自然科学版,2005,2(4):22-27

[4] 中华人民共和国铁道部.TB 10002.1-2005铁路桥涵设计基本规范[S].北京:中国铁道出版社,1999

[5] 中华人民共和国交通运输部.JTGTD64-01-2015公路钢混组合桥梁设计与施工规范[S].北京:人民交通出版社,2015

[6] 康浩.高墩大跨刚构桥施工期可靠度研究[D].北京:北京工业大学,2006

[7] 李杰.钢管混凝土高墩连续刚构桥施工期稳定性及可靠度分析[D].湖南:长沙理工大学,2009

[8] 沙丽新,石雪飞.斜拉桥主梁静力可靠性反问题分析[J].哈尔滨工业大学学报,2004,36(2):258-260

[9] 程进,肖汝诚.基于逆可靠度法的大跨悬索桥主缆安全系数评估[J].中国公路学报,2007,20(1):58-61

[10] 罗正东,苏永华,付雄,等.基于逆可靠度方法的边坡稳定性分析[J].公路交通科技,2014,31(3):43-48

Stability Safety Assessment of Cantilever Construction for High-pier Rigid Frame Bridge

QI Feng-jun1, LUO Zuo-long2*, YAO Yuan3, TAN Mei-jing4

1.710064,2.0300003.100044,4.100076,

In consideration of the limitations of current researches and applications, this paper presents a method for evaluating the safety of cantilever construction of rigid frame bridges with high piers considering the randomness of parameters by combining with nonlinear finite element results and inverse reliability method. The limit state function of structural stability load and resistance is obtained by nonlinear finite element method, the inverse reliability mathematical model was used to solve the problem. The result showed that the method can not only consider the randomness of the parameters, but also obtain more objective and reliable results, and the safe coefficient expression of the traditional method is adopted. It has good engineering application value and practical significance.

Rigid frame bridge;construction safety; assessment

U441+.2

A

1000-2324(2018)03-0504-04

2017-01-05

2017-03-06

岐峰军(1979-),男,博士研究生,高级工程师.研究方向:桥梁施工技术与工程控制. E-mail:qfjwjh0523@163.com

Author for correspondence. E-mail:luozuolong@sxu.edu.cn