Free radical reaction model for n-pentane pyrolysis
2018-05-26CongZhouYuanyiYangWeiLiYingShiLiJinZhaobinZhangGuoqingWang
Cong Zhou *,Yuanyi Yang ,Wei Li,Ying Shi,Li Jin ,Zhaobin Zhang ,Guoqing Wang
1 College of Chemical Engineering,Beijing University of Chemical Technology,Beijing 100029,China
2 SINOPEC Beijing Research Institute of Chemical Industry,Beijing 100013,China
1.Introduction
Ethylene,propylene,butadiene,and aromatics are the basic chemicals which are mainly produced by steam pyrolysis of petroleum hydrocarbons in the steam crackers.Petroleum hydrocarbons are preheated by superheated steam in the convection section of the furnace,and then the pyrolysis process takes place mainly in the radiant section of the furnace,where tubes are externally heated to 750–900 °C.Then the pyrolysis products are separated into hydrogen,ethylene,propylene,butadiene,aromatics and so on.The operating conditions,such as residence time,ratio of steam to oil,coil outlet pressure and coil outlet temperature,would affect the pyrolysis product yields.Therefore,the building of pyrolysis model to simulate hydrocarbons pyrolysis in cracking furnace is important for the technology development,furnace design,and operating optimization.
During the establishment of the pyrolysis model,the key step is the simulation of the reaction process from reactants to products and the core is the kinetic model of the pyrolysis.The pyrolysis reaction kinetic model always is the focus of the research.Based on the research results,the kinetic model of pyrolysis can be divided into three categories generally.They are simple empirical model,semi-empirical model(molecular model),and theoretical model(the free radical model).The empirical model is a prediction model based on the relationship between the operating parameters(e.g.temperature,residence time)and the material properties(e.g.specific gravity and family composition)and the product yields[1–5].According to the molecular model,the free radical reaction is generally incorporated into a molecular reaction,or a number of molecular reactions are combined into average molecular reactions.The relatively simplified kinetic model was obtained by calculating the relevant kinetic parameters[6–10].These above two models are easier to build up and run quickly.However,both models should have sufficient experimental data and they are just suitable for test conditions.The free radical model is based on Rice's free radical theory[11],and the reaction network is constructed by the elementary reaction[12–15].The free radical model can better reflect pyrolysis process with good adaptability and external ductility.But the reactants and reaction types are complex,and the number of reaction kinetic parameters is large.So the establishment and solution of the model is more difficult.
In this paper,the free radical reaction model was studied with the n-pentane pyrolysis process as an example.
2.Pyrolysis Model Development
2.1.Parameters' solution
The kinetic parameters were generally obtained from experimental study in the previous research[16].According to the pyrolysis process of petroleum hydrocarbon,lots of free radicals need to be caught and analyzed.Recently,the development of quantum chemistry has provided a new way to solve this problem by theoretical calculation[17,18].Here,the n-pentane pyrolysis process is investigated by means of quantum chemistry and Gaussian 03 Software is used to calculate the thermodynamic parameters of reactants and products.Then the kinetic parameters of the reactions are obtained.At last,pyrolysis reaction network consisting of a large amount of reactions and free radicals is constructed and the free radical reaction model for n-pentane pyrolysis is built.
2.1.1.Calculation of thermodynamic parameters
The structure of the reactants and the products involved in the reaction is optimized by Gaussian03 Software to obtain the optimized structures(the stationary points)and to calculate the frequency and the thermodynamic parameters.Then,the structure of the van der Waals complex composed of the reactants and products is optimized.The optimized structure of the reaction initiation and termination is obtained to optimize the reaction transition state.The following is the choice of calculation method in the Gaussian03 Software:Calculation accuracy and calculation amount being evaluated,UB3LYP method applies to calculate the bimolecular reactions,and UMP2 is used to calculate the unimolecular reactions.The basis set of the calculation is the level of 6-31G+(d,p).
The structure of the reaction transition state is configuration optimized with QST2&QST3 method of Gaussian03.The frequency characteristic value of the transition state of the optimized structure is calculated,and the saddle point type of the structure is determined by the imaginary number to verify the reaction transition state.Then the IRC(intrinsic reaction coordinate)is used to search the reactants in the both ends of the reaction transition state to verify whether the transition state is in the intermediate state.At last,the thermodynamic parameters are calculated under the same calculation method and basis set.
Based on the above thermodynamic parameters,the ground state energy,enthalpy of formation,entropy of formation and Gibbs free energy of the reactants,reaction transition state and the products are obtained,and the activation enthalpy(ΔH≠),the activation free energy(ΔG≠)and the activation entropy(ΔS≠)are calculated[19].
2.1.2.Solution of the reaction kinetic parameters
According to the obtained thermodynamic parameters,the reaction kinetic parameters can be calculated from the transition state theory,and the formula can be derived:

In comparison with Arrhenius Eq.(2),

The first half of the Eq.(1)is combined to the frequency factor A,and the activation enthalpy(ΔH≠)is equal to that of the Arrhenius equation.Therefore,the activation energy can be calculated from the thermodynamic parameters of quantitative chemistry calculation,and the frequency factor A can be obtained from the following equations.
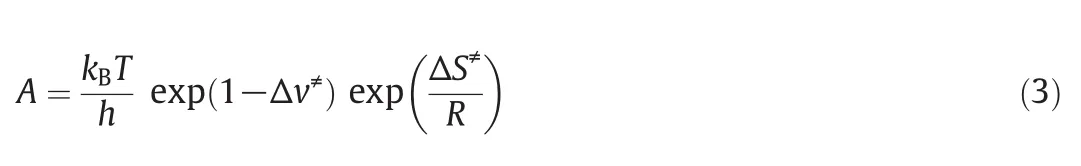
The free radical reaction of the pyrolysis of n-pentane is mainly divided into four type,i.e.initiation reaction,hydrogen absorption reaction,beta cleavage reaction and free radical coupling reaction.Here the kinetic parameters Eaand A of the four radical reactions involved in n-pentane pyrolysis are calculated,and the reaction rate constant k at different temperatures can be obtained.
The initiation reaction is taken as the example.There are two kinds of bond cleavage in the initiation reaction of n-pentane pyrolysis,i.e.C-H bond cleavage and C--C bond cleavage.The C--H bond cleavage can occur on α carbon,β carbon and γ carbon,respectively.Since the C--C bond is σ bond,the C-H bonds on the carbon atom are axisymmetric and the reactions are equivalent.Then C-H bond cleavage of n-pentane can be divided into three different situations to calculate the kinetic parameters.According to the C--C bond cleavage,the kinetic parameters can be calculated under two conditions of α carbon-β carbon bond and β carbon-γ bond breaking,respectively(Fig.1).

Fig.1.Diagram of reaction sites for pentane.
The kinetic parameters of initiation reaction of the n-pentane pyrolysis calculated under five conditions are listed in Table 1.

Table 1 Kinetic parameters of initiation reaction of the n-pentane pyrolysis
The reaction rate constants of the above five reactions under the temperature range of the common pyrolysis are calculated by Arrhenius equation.The dependence of reaction rate constant on the temperature is shown in Fig.2.The figure shows that the activation energies of these five reactions are larger,and the reaction rate increases obviously when the reaction temperature exceeds 850°C,and its absolute value is small.
In hydrogen abstraction reaction stag 60 reactions are considered,in the β cleavage reaction stage 10 β cleavage reactions and 10 reverse cleavage reactions are considered,in the free radical coupling reaction stage 9 free radical coupling reactions are considered.The reaction kinetic parameters of the above reactions are calculated.The changes of the reaction rate constants with the pyrolysis temperature are shown in Figs.3–5.
From Figs.2 to 5,it can be seen that the reaction rate constant k of the initiation reaction(Fig.2)is significantly smaller than that of the other three reaction stages in the reaction temperature range.It is indicated that the initiation reaction is the speed control step of the n-pentane pyrolysis process.
The kinetic parameters of four types of reactions,i.e.the free radical initiation reaction,hydrogen abstraction reaction,β cleavage reaction,and free radical coupling reaction,are obtained by quantum chemistry method.The obtained reaction is combined with the reaction of the pyrolysis model of C4 hydrocarbon[20],and the reaction network of pentane pyrolysis consisted of 199 free radicals reactions.
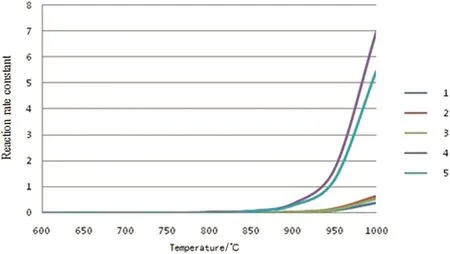
Fig.2.Rate constants of the initiate reactions[reaction rate constant,s−1(unimolecular reaction)or m3·mol−1·s−1(bimolecular reaction)].
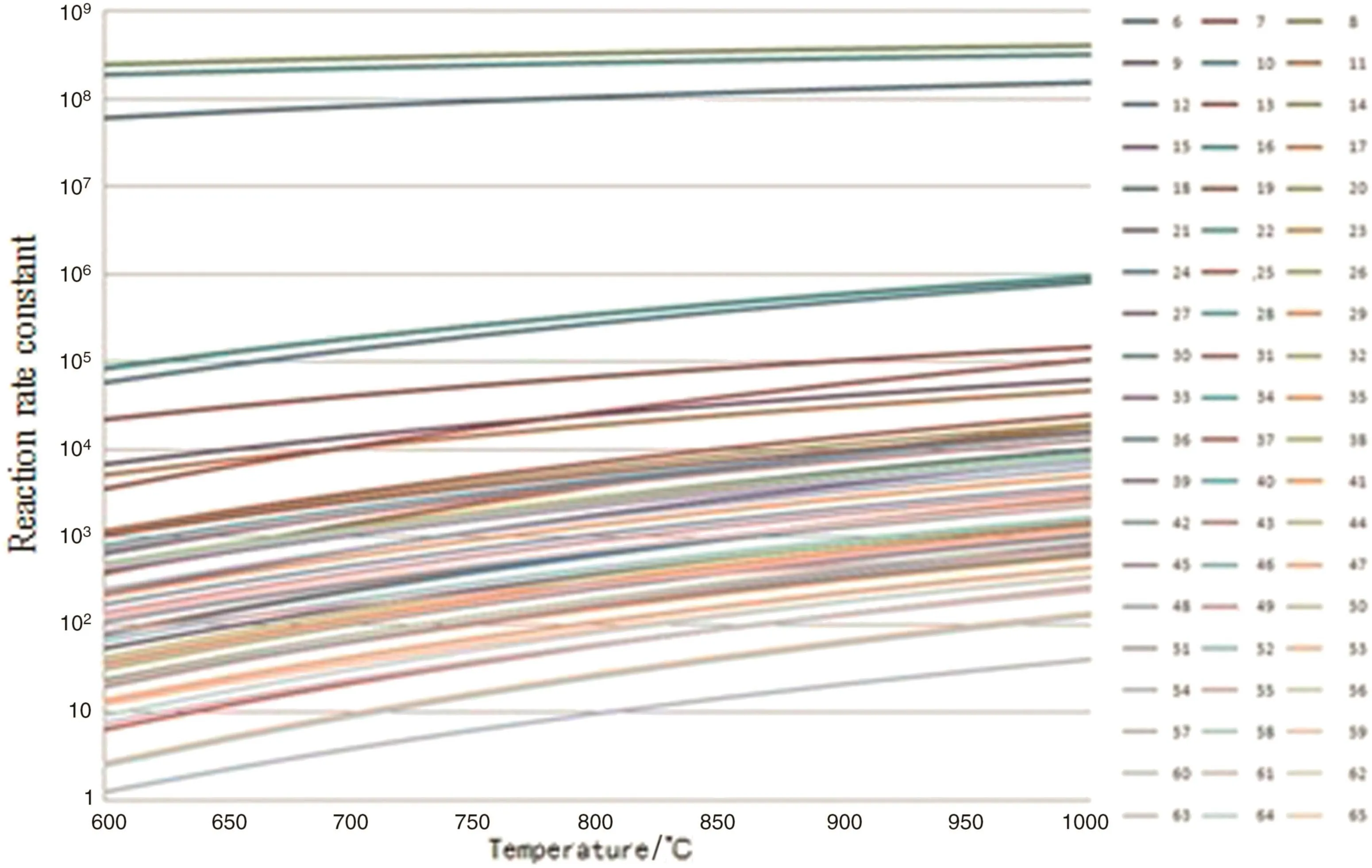
Fig.3.Rate constants of hydrogen absorption reactions[reaction rate constant,s−1(unimolecular reaction)or m3·mol−1·s−1(bimolecular reaction)].
2.2.Pyrolyisis model formulation
A plug flow model is used to simulate the radiant coil of the cracking furnace(Fig.6).The setofcontinuity equations is written with the mass,energy and momentum conservation as follows[21].

On the basis of the obtained kinetic parameters,the above set of equations is solved.The material composition,pressure,temperature and heat intensity of the reactor are calculated.The pyrolysis model is established.
3.Solution and Optimization of Kinetic Model
In the kinetic network of molecular reaction model,the set of ODEs(ordinary differential equation)consisted of fewer involved species and reactions isn't stiff.Such equation set can be solved by four-order Runge–Kutta method.
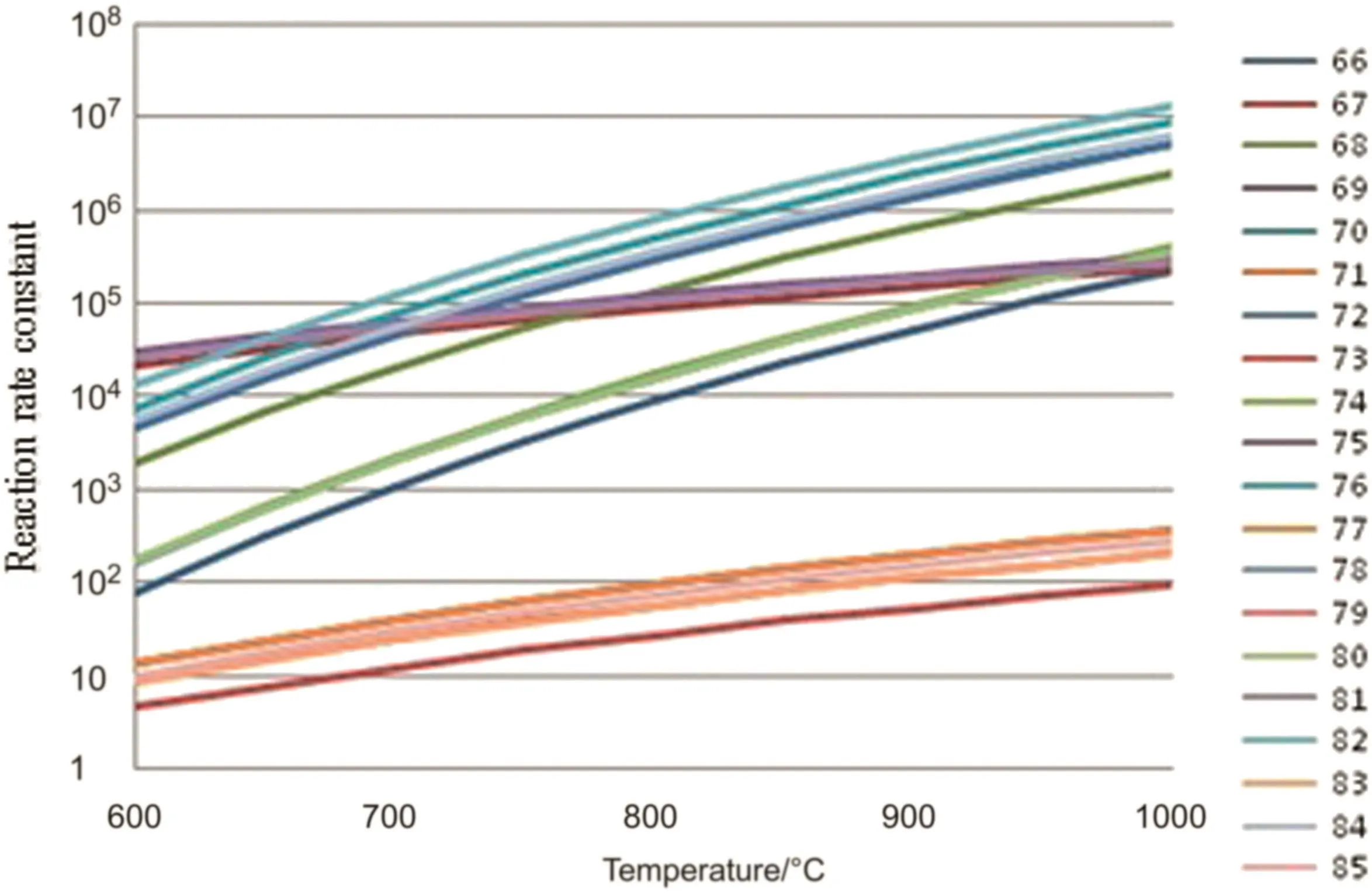
Fig.4.Rate constants of β-fracture reactions[reaction rate constant,s−1(unimolecular reaction)or m3·mol−1·s−1(bimolecular reaction)].

Fig.5.Rate constants of radical coupling reactions[reaction rate constant,s−1(unimolecular reaction)or m3·mol−1·s−1(bimolecular reaction)].
In the above kinetic model,free radical species with very low concentration emerge.It brings the stiffness for the set of ODEs.In such an ODE set,some species' concentrations change rapidly and some change slowly.The rapidly changing component can quickly reach its steady value,while the slowly changing component reaches its steady value slowly.From the view of numerical solution,when the change is fast,the small step length should be selected for the integral,when the changing component reaches its steady value,larger step integration should been chosen.But in common method such as Runge–Kutta method,the step length couldn't be enlarged with the component change,otherwise the numerical instability will occur,i.e.the error will increase rapidly,so that the solving process cannot continue[22–24].

Fig.6.Schematic diagram of the reaction tube in radiant section
So the stiff of the set of free radical reaction ODEs brings large difficulty for the solving,and the Runge–Kutta method isn't efficient for such ODE set.It is necessary to find new method to solve such ODE set.
3.1.Solution of kinetic model
The semi implicit Eularmethod is applied to solve the stiffODEs[25].The ODE d Y/d t=M(Y)+N(Y)is taken as an example.The right term M(Y)of the equation is a non-rigid term and N(Y)is a rigid term.
Explicit algorithm is as follows.
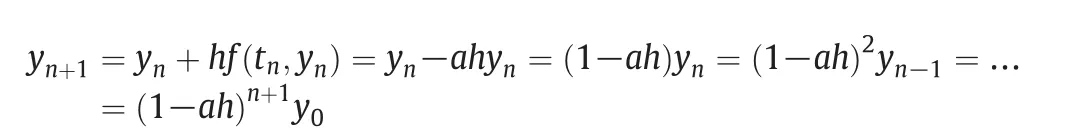
The solution of this algorithm does not need iteration,but it is not suitable for rigid problems.
Implicit algorithm is as follows.
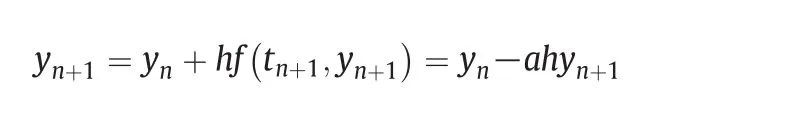
The algorithm needs to be solved iteratively with a lot of computing resources.
By means of semi implicit method,the term M(Y)is calculated by explicit algorithm and the N(Y)is calculated by the semi implicit scheme.Such solution will not only solve the problem of rigid equations,but also reduce the consumption of computing resources to improve the efficiency of the solution.
The semi implicit Eular method is used to solve the pyrolysis example,and the yield of the product is obtained,as shown in Fig.7.It can be seen that the semi implicit Eular method can solve the stiff ODEs.
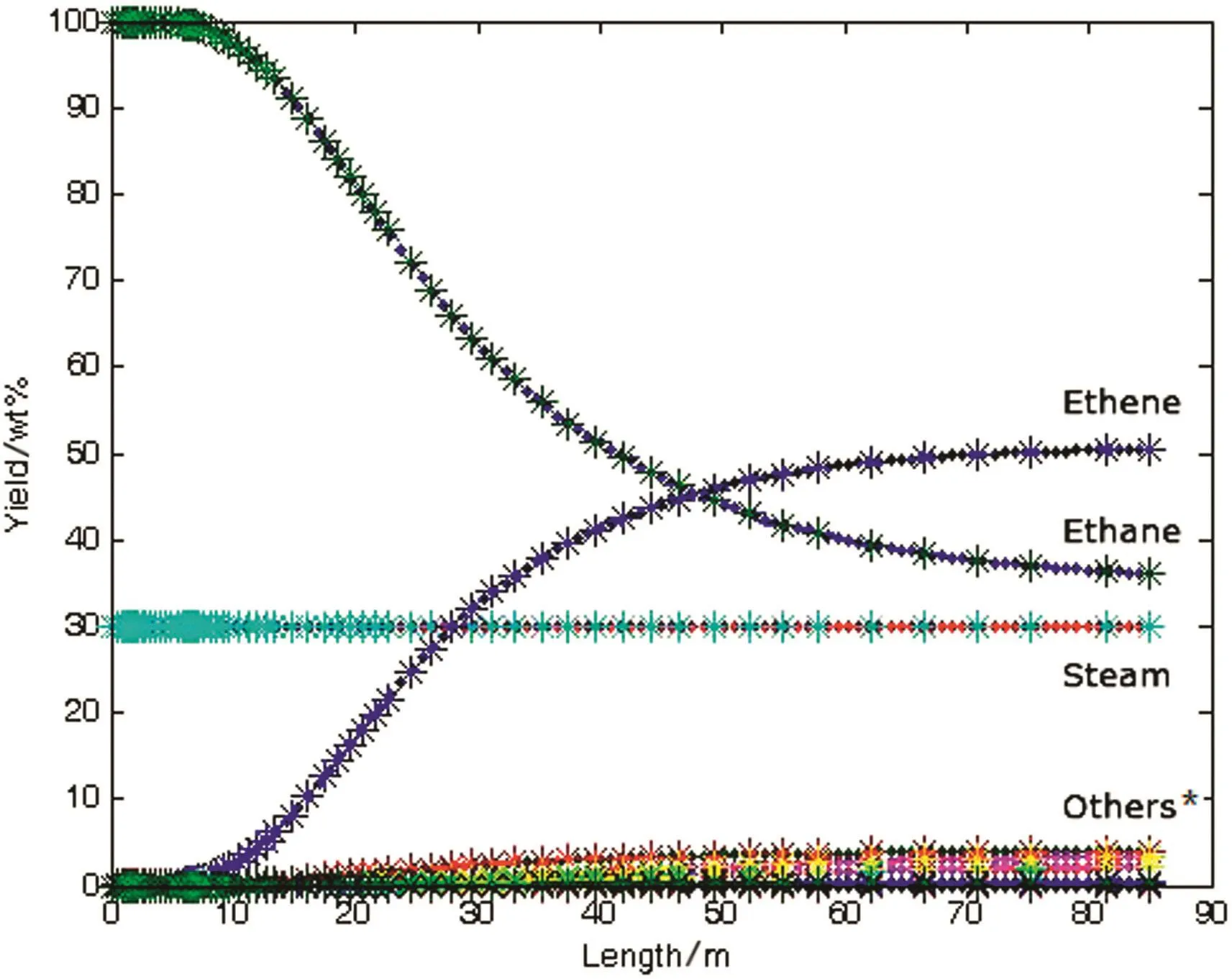
Fig.7.Chart for results from semi-Eular methods*:Others stand for minor products e.g.methane,hydrogen,propylene,butadiene,etc.
Although the solution to the problem of stiff ODEs is solved,the current calculation takes a long time.The solution shown in Fig.7 takes more than 3400 ms.The computational efficiency needs to be improved.
3.2.Optimization of solution method
The operation efficiency is improved by multi-core CPU parallel computing with OpenMP assemblies.OpenMP is a parallel processing of program assemblies presented by OpenMP Architecture Review Board[26].It can describe a high-level abstract interface for parallel calculations to reduce the difficulty and complexity of parallel programming.This software can be used in parallel computing programs to support multi-core computing system.
After the addition of the support for OpenMP in programming environment,the program blocks for parallel operation are searched.The parameters ofOpenMP are configured,such as the number of automatic opening process.Then the compiler can process these loops and call the OpenMP assembly to configure the thread granularity and load.The compiled program is running on the computer with quad-core CPU.It shows that threads optimized with OpenMP can use all the CPU resources and the execution time decrease.
After the multi-core CPU parallel computing function is implemented,the code segment of the model is processed in serial and parallel respectively,and the calculation efficiency is tested.The time consuming of optimization is presented in Fig.8.

Fig.8.Comparison chart of time-consuming of optimized semi-implicit Eular.
After comparison,the code segment with significant optimization is selected to be optimized,and the code segment without obvious optimization is keeping the serial execution.The system resource for creating threads in parallel is reduced and the delay of the inter thread information exchange is also reduced.At last,the average consuming time of the serial semi-implicit Euler method is reduced from nearly 3500 ms to 1200 ms.
3.3.Parameter optimization
In the semi implicit Eular algorithm,there are three important parameters to control the amount of calculation and the calculation accuracy of ODEs' solution,i.e.the absolute error convergence(atol),the relative error(rtol)and the initial step size(h).In the coded program,two of the above three parameters are fixed and the average time of semi implicit Eularalgorithm is scanned under the fixed interval parameter changes.The influence of parameter changes on the average time is presented in Fig.9.

Fig.9.Influence of calculation parameters on consuming time.
Fig.9 shows that with the increase of h value,the average time of the algorithm is obviously reduced,and the inflection pointis reached when the value of h is 0.1 that is the optimized value of h.With the increase of rtol and Atol parameters,the average time of algorithm is decreased obviously without obvious inflection point.But with the increase of the two parameters,the calculation accuracy of semi implicit Eular algorithm decreases.The values of two parameters are selected as those higher values in the range of accuracy requirements.

Fig.10.Schematic device of bench scale pyrolysis unit.

Table 2 Operating conditions of n-pentane pyrolysis experiments
By adjusting the three parameters of rtol,Atol and h,the average time of semi implicit Eular algorithm can be reduced to less than 300 ms.The calculation efficiency is increased by 10 times.
4.Model Verification
The verification of the kinetic scheme was performed on the basis of n-pentane pyrolysis experiments in the bench scale pyrolysis unit under the temperature range of 650 °C to 875 °C.Fig.10 is the schematic device of the bench scale pyrolysis unit.The unit can predict the yields for most of cracking coils and most of operating conditions and this unit provides valuable lots of suggestions to the ethylene plant about the operation[27].Table 2 is the operating conditions of experiments.
The comparison between measured and calculated yields of hydrogen,ethylene and propylene are presented in Figs.11–13.

Fig.11.Hydrogen yield of n-pentane pyrolysis from model simulation and experimentation.
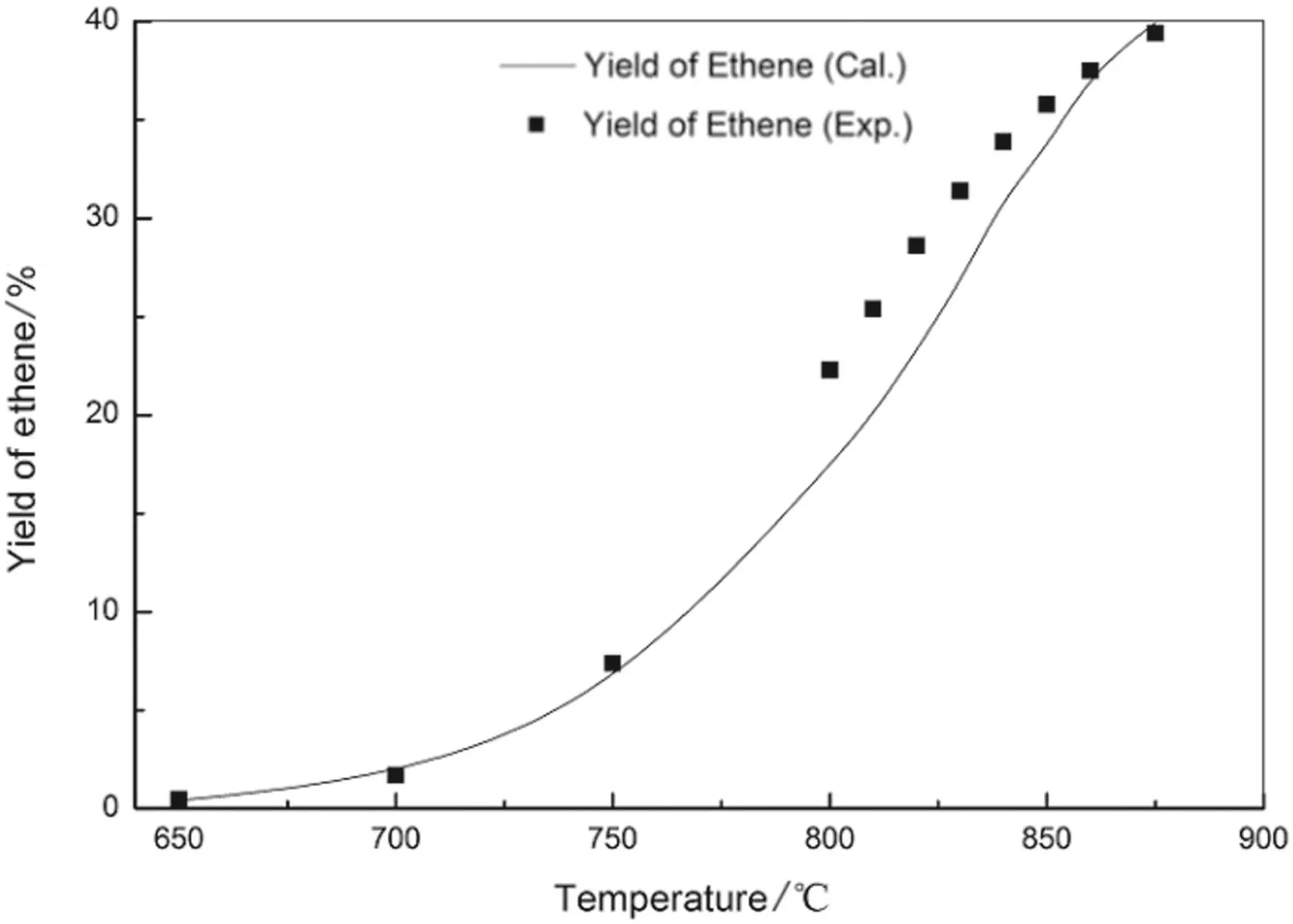
Fig.12.Ethylene yield of n-pentane pyrolysis from model simulation and experimentation.

Fig.13.Propylene yield of n-pentane pyrolysis from model simulation and experimentation.
The figures show the general favorable agreement between the predicted data and the experimental data.The experimental yields of main products are consistent with the simulated results from the above kinetic model.The validity of the above built free radical reaction model and its solution method is confirmed.On the basis,the pyrolysis network can be explored,such as increasing the number of reactions and the reaction path,to apply to more complex pyrolysis process.
5.Conclusions
A method of the establishment and solution of the hydrocarbon pyrolysis model based on free radical reaction mechanism is presented.The n-pentane pyrolysis process is taken as an example.The pyrolysis kinetic parameters are obtained by quantum chemistry and the free radical reaction net is established.The pyrolysis model is developed on the basis of the plug flow reactor model.During the solution of the model,the stiff ODEs are solved by semi implicit Eular algorithm and the computational efficiency increases 10 times by algorithm optimization.
The method is applicable to building free radical reaction model of pyrolysis process of n-pentane.It can accurately simulate hydrocarbon pyrolysis process,and effectively improve calculation speed of reaction model.Itprovides an effective method for the accurate prediction of the yields of pyrolysis products.
Nomenclature
A frequency factor,s−1(unimolecularreaction)orm3·mol−1·s−1(bimolecular reaction)
diinside diameter,m
dooutside diameter,m
Eaactivation energy,kJ·mol−1
f friction coefficient
G mass flow,kg·m−2·s−1
ΔG≠Gibbs activation free energy,kJ·mol−1
Hiheat into micro element,kJ·s−1
Hoheat out of micro element,kJ·s−1
Hrreaction heat of micro element,kJ·s−1
ΔH≠activation enthalpy,kJ·mol−1
h Planck constant,6.626196 × 10−34J·s
K overall thermal conductivity,kJ·s−1·m−2·K−1
k reaction rate constant,s−1(unimolecular reaction)or m3·mol−1·s−1(bimolecular reaction)
kBBoltzmann constant,1.3806505 × 10−23J·K−1
L length of the reaction tube,m
Nkmolar flow rate of component k,mol·s−1
P reaction pressure,Pa
R ideal gas constant,8.314 J·mol−1·K−1
rjreaction rate of reaction j,mol·m−3·s−1
S cross-sectional area of tube,m2
T temperature,K
Tfflow temperature,K
Twwall temperature,K
Vmmolar volume,m3·mol−1
βj,kstoichiometric coefficients of component k in reaction j
Δυ≠molar change of active compounds
κ(T) Wigner tunnel effect correct factor
ρ fluid density,kg·m−3
[1]D.H.Zhang,Calculation of ethylene yield for different naphtha feeds and directing evolutionary operation for cracking furnace,Petrochem.Technol.16(6)(1987)426–429.
[2]G.H.Xiong,H.Hao,Y.Wang,S.Li,Calculation of ethylene yield by hydrocarbon pyrolysis,Chem.React.Eng.Technol.12(2)(1996)161–165.
[3]W.Xu,J.S.Yu,Research of soft measurement for pyrolysis product yield with various model structures,Int.Instrum.Autom.8(3)(2004)40–42.
[4]X.F.Zhuang,J.S.Yu,Modeling of depth of fragmentation and its application,Process Autom.Instrum.25(6)(2004)31–35.
[5]S.M.Sadrameli,A.E.S.Green,Systematics and modeling representations of naphtha thermal cracking for olefin production,J.Anal.Appl.Pyrolysis 73(2)(2005)305–313.
[6]P.Kumar,D.Kunzru,Modeling of naphtha pyrolysis,Ind.Eng.Chem.Process.Des.Dev.24(3)(1985)774–782.
[7]Y.Y.Yang,Q.Q.Zeng,S.X.Xu,W.Huang,G.Z.Zou,Y.Y.Li,Pyrolysis model of heavy feedstock,Petrochem.Technol.15(1)(1986)1–9.
[8]G.F.Fromet,Kinetics,reactor design in the thermal cracking for olefins production,Chem.Eng.Sci.47(9–11)(1992)2163–2177.
[9]M.Watanabe,Overall rate constant of pyrolysis of n-alkanes at a low conversion level,Ind.Eng.Chem.Res.40(9)(2001)2027–2036.
[10]K.He,D.R.Wu,Z.F.Ma,Optimization of molecule reaction kinetics model parameter in HVGO cracking reaction,Ethylene Ind.18(2)(2006)15–18.
[11]F.O.Rice,The thermal decomposition of organic compounds from the start point of free radicals 4,the dehydrogenation of paraf fin hydrogenations and the strength of the c--c bond,Am.Chem.Soc.55(1933)4245–4247.
[12]M.Dente,Detailed prediction of olefin yields from hydrocarbon pyrolysis through a fundamental simulation model,Comput.Chem.Eng.13(1979)61–75.
[13]J.J.Dunkleman,L.F.Albright,Industrial and laboratory pyrolyses,in:L.F.Albright,B.L.Crynes(Eds.),ACS Symposium Series,32,American Chemical Societ,1976(Chap.14).
[14]A.G.Goossens,M.E.Dente,E.Ranzi,Improve steam cracker operation,Hydrocarb.Process.57(9)(1978)227–236.
[15]Zdenek Belohlav,The kinetic model of thermal cracking for olefins production,Chem.Eng.Process.42(2003)461–473.
[16]X.C.Zeng,Y.Q.Zhang,Theory and Method of Chemical Reaction Thermodynamics,Chemical Industry Press,Beijing,2003.
[17]H.Li,Z.B.Zhang,Calculation for chain initiation-termination reactions in thermal cracking:Cleavage-formation of C--H bond,Petrochem.Technol.35(2006)643–648.
[18]H.Li,B.Z.Chen,M.B.Huang,CASPT2 investigation of ethane dissociation and methyl recombination using canonical Variational transition state theory,In.J.Chem.Kinet.40(2008)161–173.
[19]W.Li,G.Q.Wang,Z.G.Du,Z.B.Zhang,L.J.Zhang,Research progress in methods for the estimation of rate constants in hydrocarbon pyrolysis,Ethylene Ind.21(2009)1–7.
[20]Z.B.Zhang,H.Li,Y.G.Zhang,S.X.Xu,S.Chen,Q.Q.Zeng,Establishment and verification of free radical model for butane steam cracking,Petrochem.Technol.36(2007)44–48.
[21]W.Li,Z.B.Zhang,C.Zhou,Y.G.Zhang,G.Q.Wang,Progress of study on free-radical mechanism model in cracking furnace tube,Ethylene Ind.22(2)(2010)1–6.
[22]S.L.Xu,C Algorithms Commonly Used Procedures Set,Tsinghua University Press,Beijing,1994.
[23]J.E.Blackemore,W.H.Corconan,Validity of the steady-state approximation applied to the pyrolysis of n-butane,Ind.Eng.Chem.Process.Des.Dev.8(2)(1969)206–209.
[24]A.S.Tomlin,M.J.Polling,J.H.Merkin,Reduced mechanism for propane pyrolysis,Ind.Eng.Chem.Res.34(11)(1995)3749–3760.
[25]W.H.Press,S.A.Teukolsky,W.T.Vetterling,B.P.Flannery,Numerical Recipes:the Art of Scientific Computing,Third edition Cambridge University Press,Cambridge,2007.
[26]B.Chapman,G.Jost,R.van der Pas,Using OpenMP:Portable Shared Memory Parallel Programming,the MIT Press,Massachusetts,2007.
[27]Z.B.Zhang,G.Q.Wang,Y.G.Zhang,S.X.Xu,Elementary study of team cracking feedstock optimization,Petrochem.Technol.37(1)(2008)8–11.
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- Numerical investigation on flow and heat transfer characteristics of corrugated tubes with non-uniform corrugation in turbulent flow
- Investigations on pool boiling critical heat flux,transient characteristics and bonding strength of heater wire with aqua based reduced graphene oxide nano fluids
- Heavy metals adsorption by banana peels micro-powder:Equilibrium modeling by non-linear models
- Potential aspect of rice husk biomass in Australia for nanocrystalline cellulose production
- Fouling evaluation on membrane distillation used for reducing solvent in polyphenol rich propolis extract
- Investigation on a vertical radial flow adsorber designed by a novel parallel connection method☆
