一种改进FSC算法在图像识别中的应用

尚 丽，孙占理

(1.苏州市职业大学 电子信息工程学院，江苏 苏州 215104；2.安徽大学 电子工程与自动化学院，安徽 合肥 230039)

掌纹识别技术可以和其他生物识别技术相融合，易于实现一体化的识别，更大程度地保证特征识别的准确性，因此成为生物特征识别技术中的一项重要研究内容[1-3]。虽然目前已研究出很多掌纹特征识别方法，但是特征识别的快速性和精确度仍是研究者追求的目标。特征识别结果的优劣和提取的特征及采用的分类器密不可分，因此选择有效的特征提取算法和分类器至关重要。

近年来，稀疏编码(sparse coding，SC)算法已被证明是一种有效的图像特征提取方法[4-6]，且在此基础上，一些改进的SC算法也被提出并有效应用于图像处理领域[6-10]，其中典型的是快速稀疏编码(fast sparse coding，FSC)算法[8]。与标准稀疏编码(sparse coding，SC)相比，FSC具有较快的收敛速度，能够实现完备基和过完备基字典的学习，可以更灵活地提取图像的特征。但是该算法没有对稀疏系数的最大化和特征向量的最大化代表性进行约束，所提取的特征用在模式识别中性能欠佳。针对这一问题，本文提出一种改进的FSC(modified FSC，MFSC)算法，并采用香港理工大学提供的PolyU数据库[11-12]进行特征提取和识别测试，讨论MFSC在图像特征识别方面的性能。文中采用目前流行的极端学习机(extreme learning machine，ELM)分类器实现掌纹特征识别任务[13-15]，同时与基于SC和FSC算法的掌纹图像分类结果进行实验对比，进一步证明了所提出的MFSC算法在掌纹图像特征识别中的有效性。

1 快速稀疏编码(FSC)

FSC算法最初由L.Honglak等[8]提出，其最小化目标函数定义为

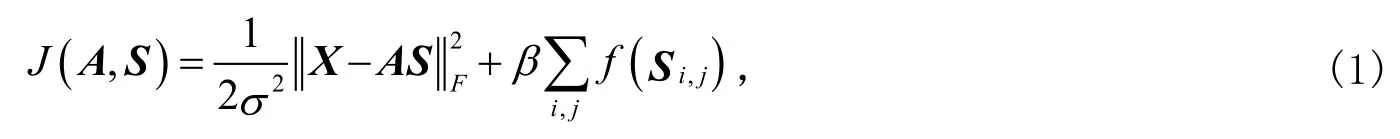
式(1)中：X=[x1，x2，…，xN]为L×N维观测样本，每一列为一个子图像块；A=[a1，a1，…，aM]为L×M维特征基矩阵，约束条件为为M×N维稀疏系数矩阵，β是一个常数；函数f(·)为稀疏惩罚函数，通常选择为如下三种形式[8]：

在L.Honglak等提出的FSC算法中，稀疏惩罚函数选择为L1正则化最小二乘形式当固定稀疏系数矩阵S时，特征基矩阵A的学习可通过最小化函数实现。考虑约束条件和拉格朗日(Lagrange)对偶函数的优势，对应的Lagrange函数形式为

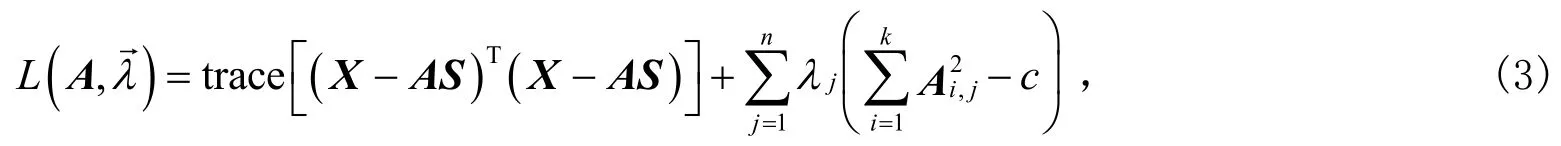
式中λ＞0是对偶变量，这样特征基矩阵A的学习就转化为求解式(3)中A的最小化问题，得到的更新公式为

固定矩阵A，对式(1)采用特征符号搜索法实现系数矩阵S的学习，具体过程参见文献[8]。这种FSC算法有效地解决了L1和L2范数的正则化及约束最小二乘法两个凸优化问题，计算过程大为简化，具有较快的收敛速度。

2 改进的快速稀疏编码(MFSC)

2.1 目标函数

为了更有效地提取图像的特征以利于后续的图像特征分类任务，在FSC算法的基础上，考虑最小化两个约束条件，本文提出了一种MFSC算法，其目标函数定义为

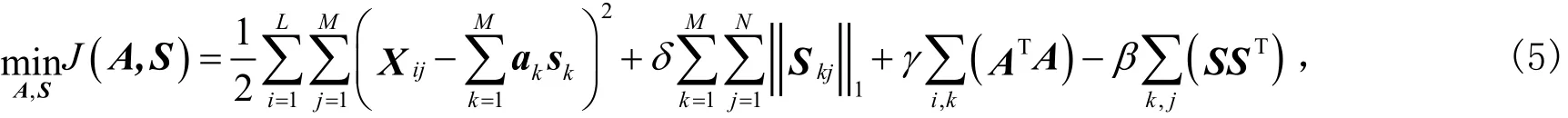
式(5)中：矩阵X，A和S与式(1)中的含义相同；约束条件为γ和β为正常数；最小化是为了增强矩阵S的最大化稀疏性，而最大化(即最小化则是为了增强矩阵A的最大化代表性。

2.2 特征基和特征系数的学习

同SC和FSC算法一样，MFSC算法仍采用轮流更新A和S的方法实现目标函数式(5)的最小化[8]。当固定S时，式(5)可以改写为

式(6)即为具有二次约束的最小二乘法优化问题，通常采用梯度优化算法可实现目标函数的最小化。为了得到更好的优化效果，本文采用Lagrange对偶法求解。式(6)对应的Lagrange函数形式为

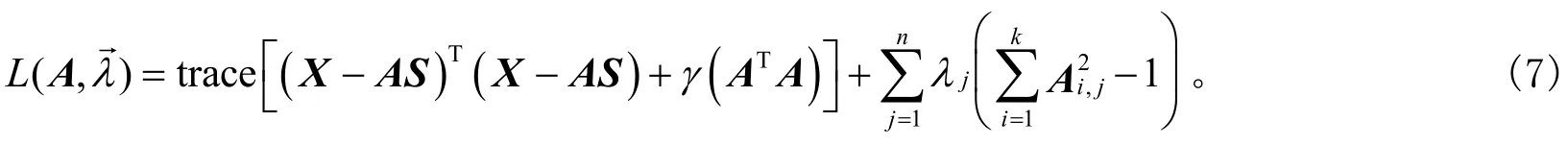
式(7)对应的Lagrange对偶函数形式为

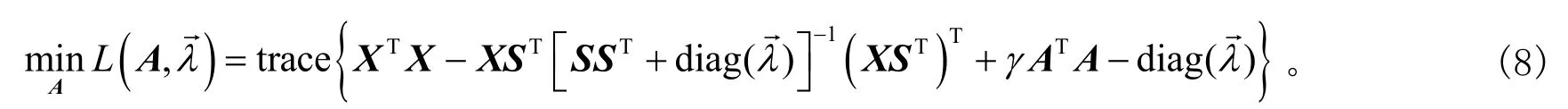
利用共轭梯度法得到矩阵A迭代公式

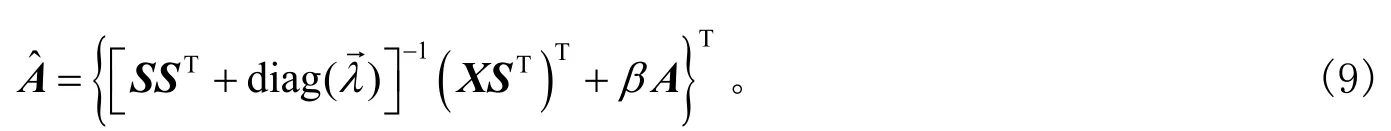
固定矩阵A，式(5)的最小化问题则转化为对每列向量s(k)j求解最小化问题

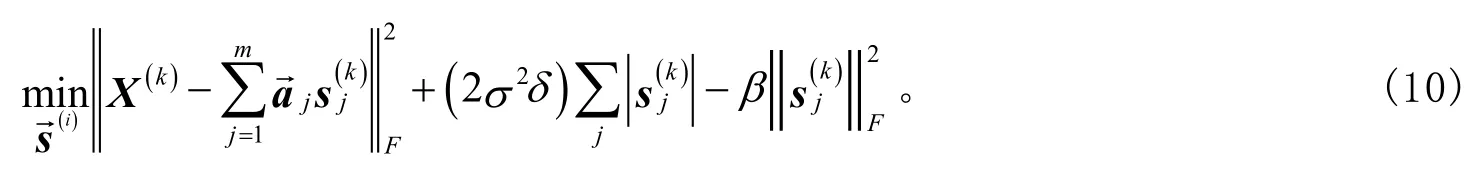
考虑稀疏向量的符号，式(10)的优化问题简化为求解下面的优化问题

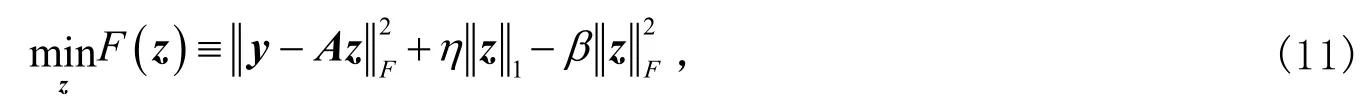
式(11)中：z表示输出向量；y表示输入向量。对式(11)进行优化时，在每个迭代步骤中首先采用梯度优化算法对向量z进行更新，得到的向量记为，则有

然后把当前的z～值代入函数式，对该函数式借助特征符号搜索法[8]进行z～的更新，其更新公式为

式(13)中：为矩阵A的子矩阵为θ中去掉零值后的符号矩阵的子向量利用

式(12)和式(13)，经过反复迭代后，最后得到最佳的系数向量，最终实现矩阵S的更新。

3 ELM分类器

极端学习机(ELM)可以随机地确定单隐层网络的输入权值和隐层节点参数，通过简单地计算可解析地获得输出权值，具有较快的学习速度和较好的泛化能力[13-15]，目前已被广泛应用于模式分类任务中[16]。ELM被用作分类器时，其分类原理与支持向量机(support vector machines，SVM)一样，也是基于两类的分类问题[13]。设为N个训练样本，其中xi=[xi1，xi2，…，xik，…，xin]T为第i个样本向量，yi=[yi1，yi2，…，yik，…，yin]T是xi对应的类别标记向量，则定义判决函数的数学模型为

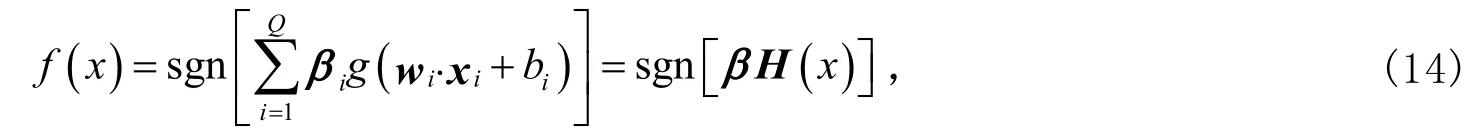
式(14)中：wi=[wi1，wi2，…，win]T是输入节点与第i个隐层节点的输入权值向量；βi=[βi1，βi2，…，βin]T是连接第i个隐层节点与输出节点的输出权值向量；bi是第i个隐藏神经元的偏置；g(·)表示隐藏层的激活函数，本文选取为Sigmoid函数；wi.xi表示wi和xi的内积；H(x)表示隐藏层输出矩阵，定义为

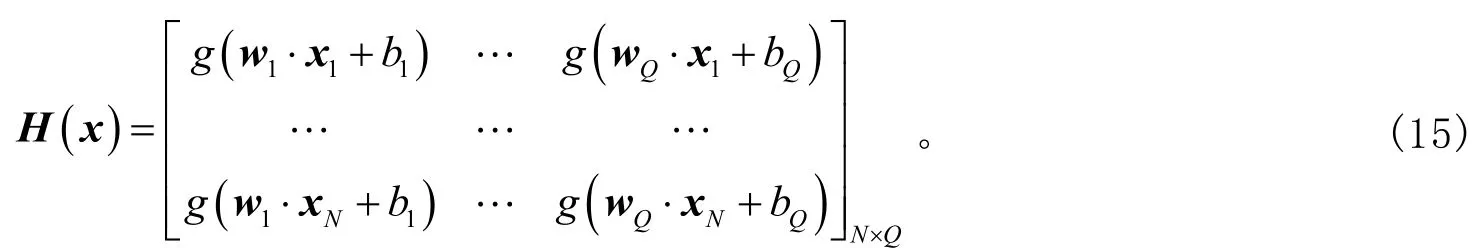
用在模式分类问题中，所采用的ELM最小化目标函数定义为

约束条件为yiβ.h(x)≥1-ξi，ξi≥0(i=1，2，…，N)。式(16)对应的Lagrange函数形式为

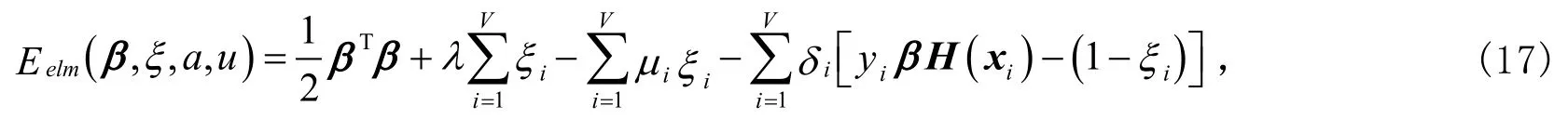
式中μi和δi为Lagrange乘数，均为负数。对β和ξ分别求偏导数，即得到和λ=δi+μi，∀i的对偶问题，则式(17)的最小化问题转化为求解目标函数

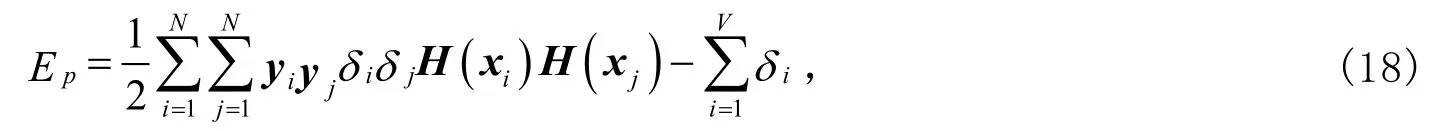
式中0≤δi≤λ(i=1，2，…，N)。根据Karush Kuhn Tucker条件[15]，当δi=0时，yiβ.h(x)＞1；δi=λ时， yiβ.h(x)＜1；0＜δi＜λ时，yiβ.h(x)=1。

4 实验结果与分析

测试中选用香港理工大学提供的PolyU掌纹数据库，该数据库包含100人的共600幅图像，即每人有6幅掌纹图像，每一幅图像被处理为128×128像素。选用每人的前3幅掌纹图像组成训练集合，后3幅掌纹图像组成测试集合。为了减少计算量，对每一幅掌纹图像采用小波变换进行预处理，得到大小为64×64像素的图像。因此，得到的训练集合Xtrain和测试集合Xtest大小均为4 096×300像素。进一步采用主分量分析(principal component analysis，PCA)方法进行降维处理，考虑不同的主分量个数，同时采用距离分类器和ELM分类器对PCA特征进行识别，以确定最佳的主分量个数，从而减少后续MFSC特征识别的计算量。采用上述两种分类器对PCA特征识别的结果，如表1所示。当维数增大时，距离分类器识别效果增强，但是ELM分类结果在主分量大于324时，识别效果相差并不很明显。因此，在考虑计算量和特征识别效果时，本文选择主分量的个数为324。则用于MFSC算法的训练集合大小Vk为300×324，每一行为一幅图像。

在324个主分量特征空间内进行MFSC特征提取学习，设训练得到的特征基矩阵为A，W=A-1，则稀疏特征系数，则测试图像的特征基为Utest=R(WWz)-1，其恢复结果可以由式得到。图1给出了采用MFSC算法训练得到的部分基图像，显然，所得到的基图像同稀疏编码特征基一样，具有局部性和方向性，模拟了人眼初级视觉系统的特性[4-5]。

进一步采用ELM分类器对MFSC特征进行识别，同时与FSC和SC特征识别结果进行对比，所得到的识别结果如表2所示。观察表2中数据，在分类器选定时，基于MFSC特征的分类效果明显优于基于FSC和SC特征的识别结果，而基于SC特征识别的结果最差。在算法选定时，ELM分类器的性能明显优于距离分类器的性能。另外，在测试中采用ELM分类器时，在每一种算法下特征识别的时间相差不明显，均为0.001 5 s左右；而采用距离分类器时，特征识别的时间明显比ELM长。因此，根据实验结果，采用基于MFSC特征的ELM分类器可以快速、有效地实现掌纹图像的识别。

图1 基于MFSC算法的部分特征及图像

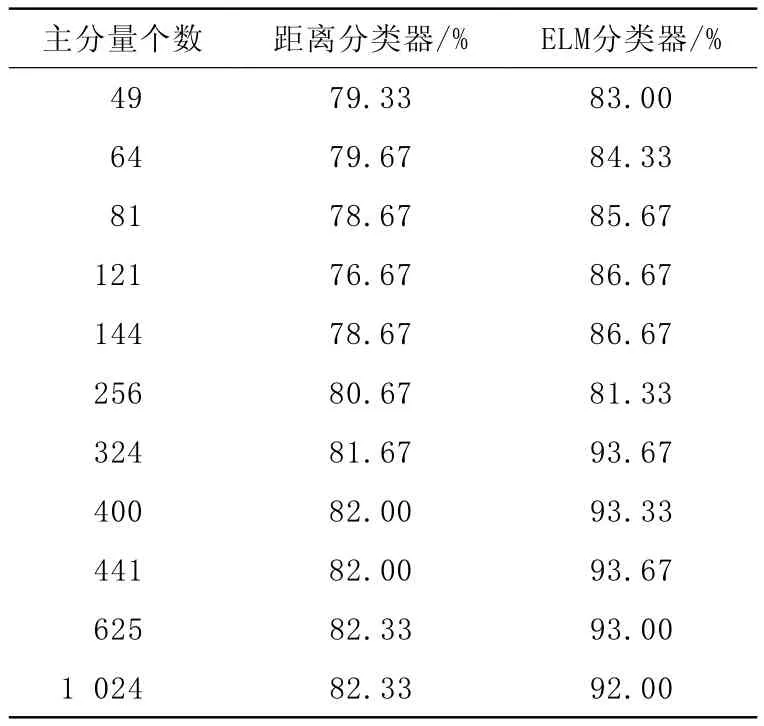
表1 PCA特征识别结果

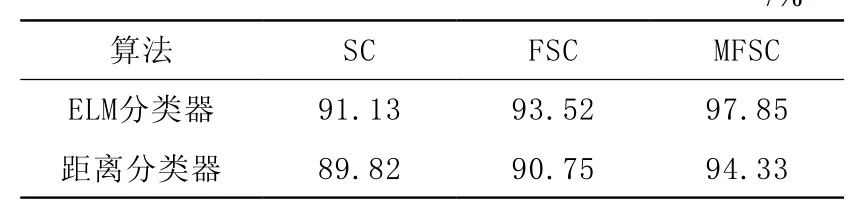
表2 不同算法下得到的识别结果

5 结论

本研究提出了一种改进的快速稀疏编码算法，并有效地应用于图像特征识别。由于该算法考虑了图像特征稀疏系数的最大化和特征基的最大表示性，有利于提高图像特征分类的精度，在应用于掌纹图像特征识别时取得了较好的识别效果。与基于FSC和SC算法的掌纹图像识别方法相比，测试结果表明本文提出的掌纹特征识别方法，具有较高的准确度和快速性，具有一定的实用性和重要的理论研究意义；而且本研究提出的方法，可以扩展应用于其他模式识别领域，具有重要的借鉴意义。

参考文献：

[1]薛延学，刘一杰，刘超，等.一种改进的BDPCA掌纹识别方法[J].计算机工程与应用，2014，50(15)：150-152.

[2]陶筱娇，王晅.基于SURF特征与模糊推理的掌纹识别[J].计算机工程与应用，2016，52(1)：185-189.

[3]MALVIYA R，KUMAR R，DANGI A，et al.Verification of palmprint using Log gabor filter and comparison with ICA[J].International Journal of Computer Applications in Engineering Sciences，2011(S)：222-227.

[4]SHANG L，HUANG D S，DU J X，et al.Palmprint recognition using FastICA algorithm and radial basis probabilistic neural network[J].Neurocomputing，2006，69 (13/14/15)：1782-1786.

[5]OLSHAUSEN B A，FIELD D J.Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J].Nature，1996，381：607-609.

[6]黄宏图，毕笃彦，查宇飞，等.基于笛卡尔乘积字典的稀疏编码跟踪算法[J].电子与信息学报，2015，37(3)：516-521.

[7]SHANG L.Adaptive denoising using a modified sparse coding shrinkage method[J].Neural Processing Letters，2006，24(2)：153-162.

[8]HONGLAK L，ALEXIS B，RAIAT R，et al.Efficient sparse coding algorithms：advance in neural information processing systems (NIPS2006)，Vancouver，B.C.，Canada，December 4-7[C].USA：MIT Press，2007：801-808.

[9]LI Qingyong，LIN Dacheng，SHI Zhongzhi，et al.Task-oriented sparse coding model for pattern classification[C]//WANG L，CHEN K，ONG Y S，et al.Lecture Notes in Computer Science (LNCS)：The 11th International Conference on Natural Computation (ICNC’05).Berlin Heidelberg：Springer-Verlag，2005：903-914.

[10]ZHANG K H，ZHANG L，YANG M H，et al.Fast compressive tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36(10)： 2001-2015.

[11]尚丽，崔鸣，杜吉祥，等.应用非负矩阵分解和RBPNN模型的掌纹识别方法[J].计算机工程与应用，2012，48(4)：199-203.

[12]郭金玉，刘玉芹.鲁棒主元分析在掌纹识别中的应用[J].计算机工程与应用，2012，48(19)：8-10.

[13]HUANG G B，CHEN L.Enhanced random search based incremental extreme learning machine[J].Neurocomputing，2008，71(16)：3460-3468.

[14]陈鸿星.基于ELM-LSSVM的网络流量预测[J].计算机工程与应用，2015，51(24)：73-77.

[15]张敏，曾新苗，马长春，等.一种基于簇的极限学习机的在线学习算法[J].计算机工程与应用，2014，50(11)：188-191，266.

[16]王梦珍，刘立，王建，等.基于Kmean和ELM的乳腺肿块检测方法[J].计算机工程与应用，2015，51(12)：171-175.