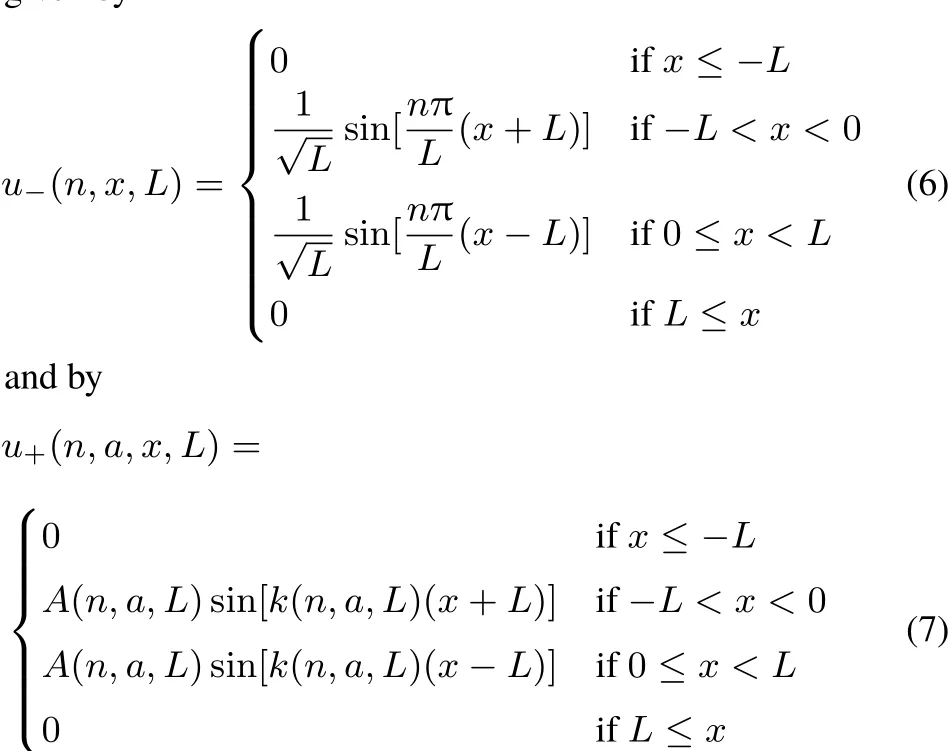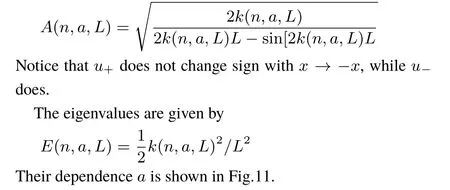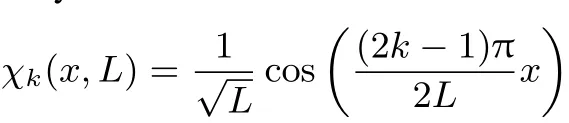Chem ical Bond ing and In terp retation of Tim e-Dependen t Elec tronic Processes w ith Maxim um Probability Dom ains
2018-05-25SAVINAndreas
SAVIN Andreas
Laboratoire de Chim ie Théorique,CNRS,and Sorbonne Université,UPMC Univ Paris 06,4 place Jussieu,F 75252 Paris cedex 05,France.
1 Introduction
Many tools have been developed to describe chem ical bonding using quantum mechanics.But chemical bonding changes during structuralmodificationsof themolecules.Does assigning spatial domains to electron pairs(the Lew is perspective)survive in time-dependent processes?Usual chemical routineuses curved arrows,suggesting that this is the case.Quantum chemical calculations performed along the reaction path tend to confi rm it.But is this adiabatic picture correct?
This paper uses a simple model,of two independent particles of the same spin,in a one-dimensional box.(As the formation of the Lew is pairs is mainly due to the Pauli principle,and only independent particles are discussed in this paper,the treatmentof two electrons of the same spin is easily transposed to the treatmentof two electron pairs.)Atstart,each of the the particles is confined to a half-box.Thewallbetween boxes becomes transparentw ith time,allow ing the particle to pass from one half-box to the other.A fter some time,τ,the wall completely disappears.
Using a “reasonable” definition,one can attribute a spatial domain to one of the electrons,the other one being in the remaining space available.This evidently workswhen thewall is impenetrable.One may naively believe that making the separation wall vanish does not qualitatively change the situation,that the Pauli principle forces the two electron pairs to remain as such,whether they are separated by awall,or not.However,aswe consider amodel for a chem ical reaction,we should look at the influence of time on the electron localization domain,and whether it aあects our perception of electron localization.
The timeevolution is computed using
(1)theadiabatic approximation,validwhen the Ham iltonian changes very slow ly w ith time,
(2)the sudden approximation,valid when the change of the Hamiltonian is fast,
(3)an explicit solution of the time-dependent Schrödinger equation,for a finite basis set,and given parameters of the system.
For amore precise definition of“slow”and “fast”,see,e.g.1,Section XVII.
The calculations below show that w ith the last two approaches,for certain time intervals,electrons are not essentially confined to the half-boxes,in contrast to a Lew is-like concept.One can find thatone electron(or electron pair)is located in the center of the box,while the other is delocalized over the remaining leftand rightparts.
The simplicity of themodel allows presenting the detailed structure of the wave function.Pictures are presented using other interpretative tools that can also be used for more complicated systems(localized orbitals,the density,and its second derivative,the electron localization function,and the maximum probability domains).It is concluded that the latter method is preferable to describe time-dependent processes,although one should keep inm ind that the present calculations are far from being representative for realsystems.
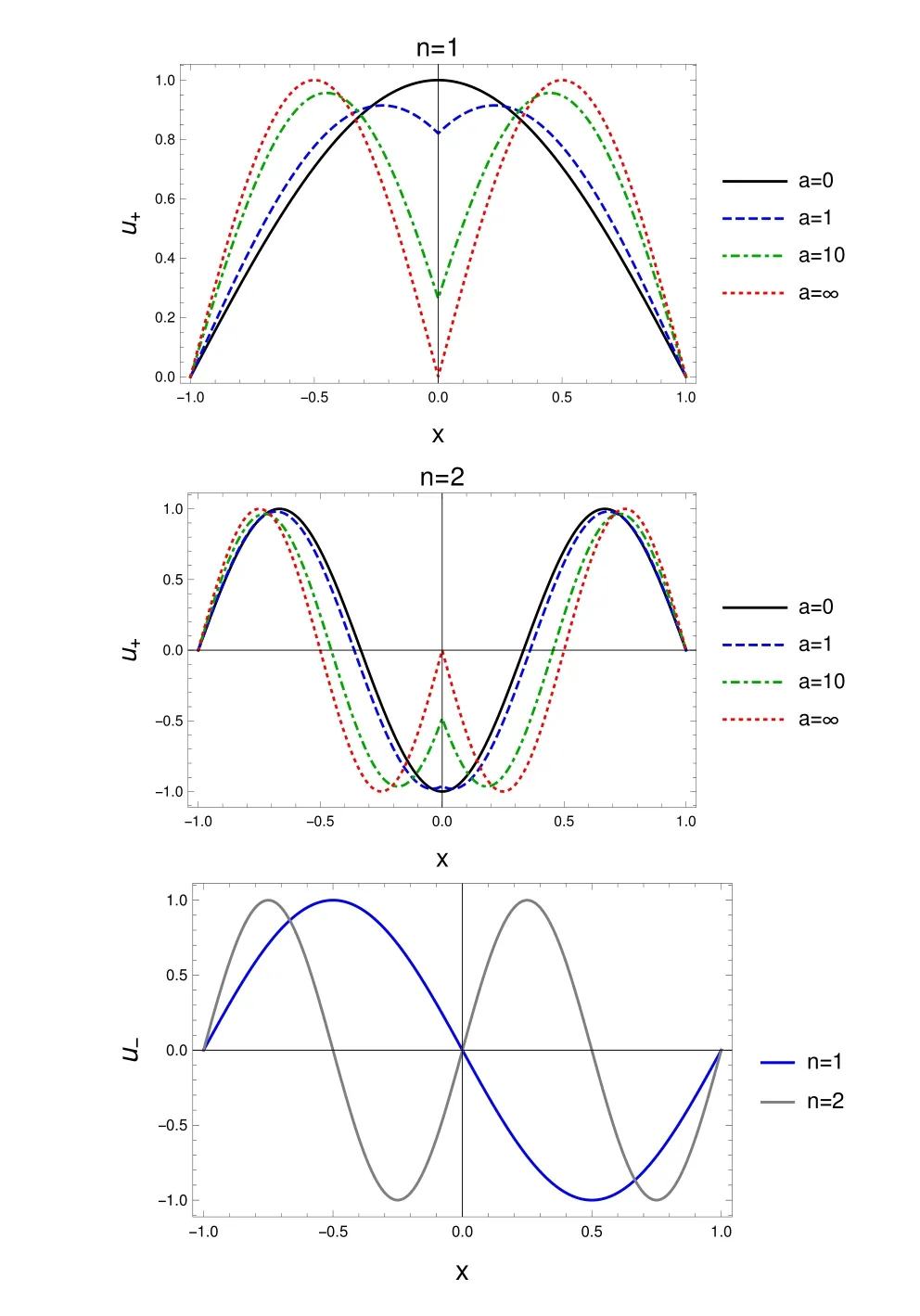
Fig.1 One-particleeigenfunctionsof the stationary Schrödinger equation for a particle in a box w ith an opaquewall;symmetric solutions u+,for n=1(top),for n=2(center),for diあerent valuesof theopacity param eter a,and antisymm etric solutions u−(bottom),for n=1,2.
2 System
2.1 Ham iltonian
A one-dimensionalbox stretching from−L to L isseparated at x=0 by an opaquewall(see,e.g.2,problems19,20).The potential isgiven by:
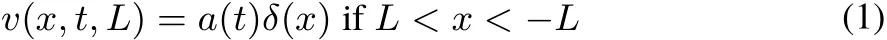
and is infinite outside this interval.The parameter a defines the “opacity” of the wall.For a=0 there is no separation between the two half-boxes(corresponding to x<0,and x>0,respectively).For a=∞there is no communication between them:the wall at x=0 is impenetrable,and each electron is confined to itshalf-box.In thispaperweconsiderthattheopacity parameter a can changew ith time,t.To simplify notation,L is dropped when equal to 1.
2.2 Stationary so lutions
The solution of the stationary Schrödinger equation for this potentialisanalytically known.By thesymmetry of thepotential v(x),there are two typesof solutions,
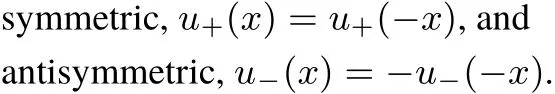
The antisymmetric solutions have a node at x=0,and are thus notaあected by the term aδ(x)appearing in v(x),Eq.(1).The explicit formsof u±are given in Appendix A.Fig.1 shows u+(n=1,x,a),and u+(n=2,x,a)for diあerent values of the parameter a,aswell as u−for n=1,2.Please notice the notch in u+produced by aδ(x)becom ingmore pronounced as a increases(atgiven n).
2.3 A trip let non-in terac ting tw o partic le system
Themodel system studied in this paper consists of two noninteracting ferm ions,in a triplet state.In fact,it stands for a system for two non-interacting electron pairs in a singletstate.Having another two electronsw ith opposite spin changes little to theproblem,as theanti-symmetrization needs to bedoneonly among particles of the same spin.The properties of this noninteracting system can be computed from awave function that is a product of two identical two-by-two Slater determ inants,one for each spin(see,e.g.3).It is thus suきcient to analyze only one of them,the properties of the four-electron system beingunderstood easily from thoseof thesame-spin twoelectron system.For example,ifwe have the density of the system w ith two spin-up electronsin the tripletstate,we justhave tomultiply itby two to obtain thatof the four-electron system.
The repulsion between electronshasbeen neglected because the formation of electron pairs isnotdue to electron repulsion.The intuition of Lew iswas that Coulomb’s law is not valid at shortdistances,and that“each pairofelectronshasa tendency to be drawn together”4.Although theexplanation given by Lew is is not correct,such an eあect is seen inmean-fieldmodels like Hartree-Fock;localized orbitalsw ith diあerentspin are pairw ise identical in the spatial part.It is the Pauli principle that keeps the electronsw ith same spin apart,and it actswhether or not they interact.Opposite spin electronscan share the same spatial domain,and can form thepairsdescribed by Lew is.In fact,many of the tools used to analyze the chem icalbond only exploit the Pauliprinciple.
Another reason not to introduce repulsion in the present calculations is that there is not a clear way how repulsion should be treated in one dimension.The Coulomb interaction in one dimension,1/|x1−x2|producesa severe singularity at x1=x2,and the volume elementdoesnotmake itvanish,as it does in three dimensions.Softened Coulomb repulsion has to be used(see,e.g.5).Physically,this is easy to understand:electrons can better avoid each other in three dimensions than in one dimension.
2.4 Analogies
In order to see a connection to chemistry,we can imagine someanalogue.Forexample,one could consider two Heatoms getting closer.From the Lew is pairing perspective,nothing interesting can be expected:even for He2,the electron pairs stay on each of the atoms.
In analogy to amolecule formation in time,we startw ith the particles separated by an infinitewall,a=∞(or,w ith a very large value).As time evolves the opacity parameter a goes to zero so that the particles finally do notsee awallat x=0,and canmove freely in thewhole box,from−L to L.
3 Too ls to analyze the electron d istribution
Therearemany tools to analyze theelectronic structure.Just a few areused below,and arenow shortly described.
3.1 Wave func tion
Onecananalyzethewave function.Ingeneral,ithasatoohigh dimension.For our example,it is only in two dimensions(the coordinate of each of the particles),and can be easily plotted.
In order to avoid the dimensionality problem,Artmann6proposed to locate themaxima of thewave function.This is a very appealing proposal,welladapted tomethod like Quantum Monte Carlo7.Ithas the disadvantage that thewave function can presentseveralmaxima,and onehas to chooseamong them.This can be avoided inmany practical situationsby choosing a domain around them8.
3.2 Maxim um p robability dom ains
Oneway to definea spatialdomain is to consider theone that maxim izes the probability to have a given number of particles,ν,in it9,the “maximum probability domains”(MPDs).In our example,we search fora domainΩ,such that the probability tofind one(and only one)particlein it

ismaximal.Ωmeans that the integration is performed only overΩthatmay,butmust not be spatially disconnected;the prefactor N,the numberof particles in the system,is due to the indistinguishably ofelectrons.
3.3 Density
A simple three-dimensional quantity is the electron density,ρ,
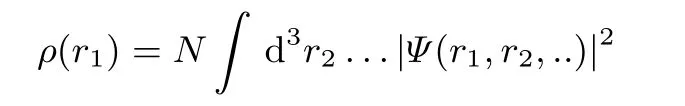
Itsanalysisand use hasbeenmuch promoted by Bader10.The particle density should not be confused with a probability densZi t y,as
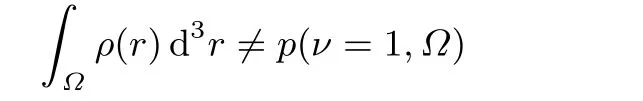
This integral over the density gives the average number of particles inΩ.
3.4 Second density derivative
Themaxima of−∇2ρare used to indicate where electron pairs localize(see,e.g.10,Section 7.1.4).Here,asoursystem is in one dimension,−isused.
3.5 Elec tron localization func tion
Another popular quantity to detect the Lew is pairs is the electron localization function(ELF)11.It isa function defined in each pointofspace,takig valuesbetween0 and 1.For regions where electrons localize,the values of ELF should be large.It has been generalized to time-dependent processes,TDELF12.In this paper,we use a formula that ismodified for particles in one dimension.The explicit expression of ELF is given in the Appendix B.
As we deal w ith independent particles,we do not have to worry aboutgeneralizations of ELF forwave functions beyond a single Slater determ inant.
3.6 Localized orbitals
Localizedorbitalsprovideasimpleinterpretation tool,andare also beused below.Forexample,for thestationary lowestenergy solution,the localized orbitalsare just the linear combination of thetwo lowestenergy canonicalorbitalswith diあerentsymmetry,[u+(n=1,x,a)±u−(n=1,x,a)]/2.Inversion,x→−x,transformsone localized orbital into the other.
4 Resu lts
4.1 Ham iltonian changes s low ly w ith tim e
Letus fi rstconsider systemswhere the Ham iltonian changes slow ly w ith time.In this case,one can simply use the solutions of the stationary Schrödinger equation,ateachmoment t.This is themostw idely used treatment.For example,one solves the Schrödinger equation on points on the reaction path,and uses oneof thebonding interpretation toolsavailable.
Corresponding to thisimage,itissuきcientto presentpictures obtained for diあerentvalues of the opacity parameter a.To get an order-of-magnitude idea of how a changes w ith time,see Appendix C.
As expected,our system turns out to be uninteresting.All themethodsmentioned above give the same result that can be summarized as “one electron in each of the half-boxes”,atall times.Of course,this statement is strictwhen a=∞,and is only qualitatively validwhen a is finite.Fig.2 showsthatonly the extreme cases,when there isan impenetrablewallseparating the half-boxes(a=∞),and when there is no separation(a=0).A discussion of this figure follows,in order to prepare that of the follow ing section,when a new situation showsup.
Thewave function,for a=∞,isstrictly localized in each of the half-boxes(it is zero when x1is in one half-box,and x2in theother).When thewallis removed,thewave function slightly extendsover the otherhalf-box(Fig.2a).
In accordancew ith it,the perfectly localized orbitals for a=∞,slightly delocalize,even for a down to 0(Fig.2b).
The density shows two peaks,each centered in a half-box;−ρ(x)hasalso suchmaxima(Fig.2c and Fig.2d).
ELF takes the maximal value(=1)when the half-boxes are separated,and each of the electrons is localized in one of them(Fig.2e).When a=0,ELF decreases,but only in the wall region,show ing again the localization of particles in the half-boxes.
Fig.2f shows the probability of finding one electron between x
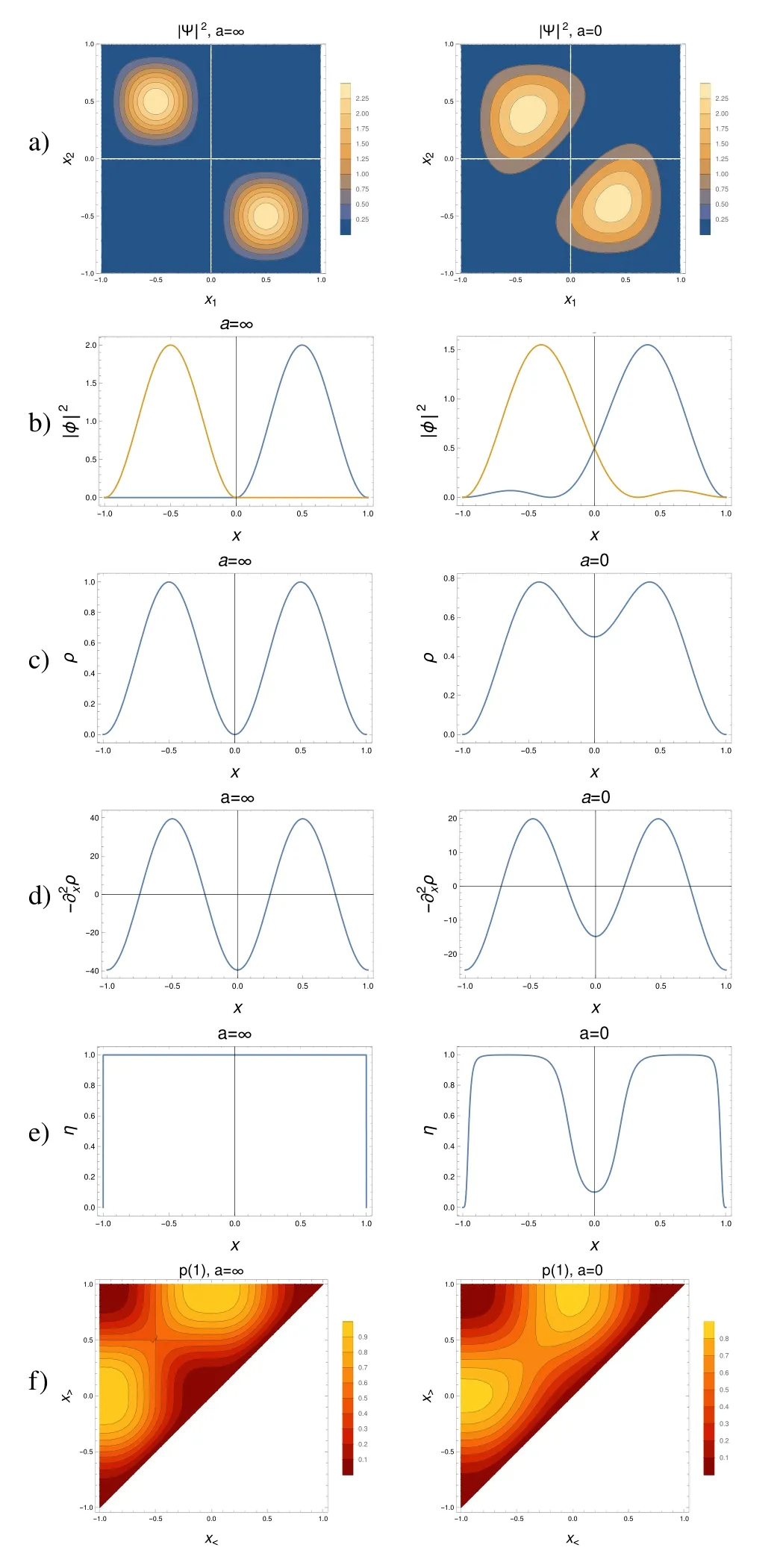
Fig.2 Slow changeof the Ham iltonian w ith time.From top to bottom:a)absolute valueof thewave function squared,as function of the coordinatesof the particles,x 1,x 2,b)localizedmolecular orbitals,c)density,d)m inus the second derivativeof the density,e)theelectron localization function,f)the probability tofind one,and only oneelectron between x
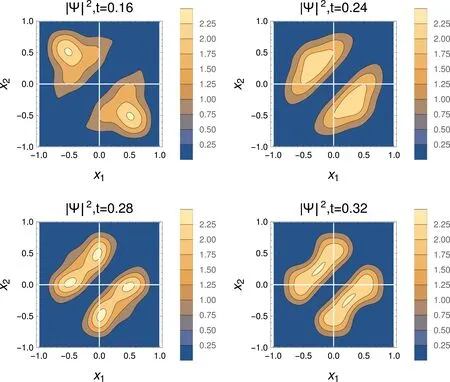
Fig.3 Absolute valueof thewave function squared,for a sudden changeof the Ham iltonian asa function of the coordinatesof the particles,x 1,x 2.The tim eafter the changeof the Ham iltonian is given in atom ic units(1 a.u.≈24 attoseconds),for L=1.
4.2 Sudden change of the Ham iltonian
4.2.1 Mathematicaldescription
Weconsidernow theoppositeextreme,when themodification in time occurs w ith a jump,from the Hamiltonian w ith a=∞ to that w ith a=0.We recall that all the u−states are unaあected by theperturbation(thatispresentonly atthenodeof these functions).After the Hamiltonian has changed,u+(n=1,x,a=∞,L)is not the ground state anymore.We expand the initial state,u+(n=1,x,a=∞,L)on the final states,u+(k,x,a=0,L),
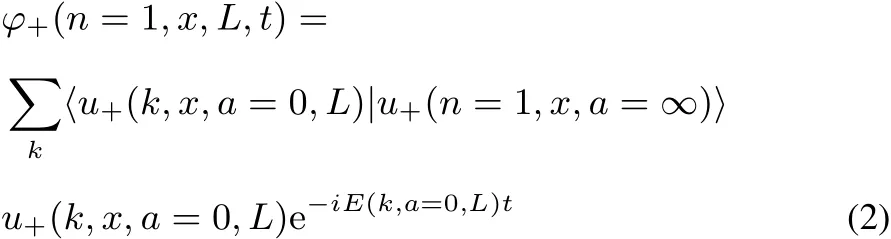
This expression shows how excited states of the stationary Schrödinger equation for the final Hamiltonian participate to thewave functionϕ+.
4.2.2 Wave function
Theevolution of the squareof the two-particlewave function w ith time ispresented in Fig.3.The starting point(t=0)is that shown for a=∞in Fig.2.At the very beginning of the process each of the particle remains highly localized in its half-box.However,the particles “realize” that they havemore space at theirdisposal,and starttoexpand(t=0.16).A broadmaximum appears later(t=0.24),and its nature is understood a short time later(t=0.28).Thewave function hasmaximaat x1=0,x2≈0.5,etc.:while one of the particles is in the center of the box,the other particle can be in eitherof the half boxes.This is followed,by another broad maximum(t=0.32),followed by again a situation as for t=0.28,etc.,until the particles retract to the initialhalf-boxes,and the processstartsagain.
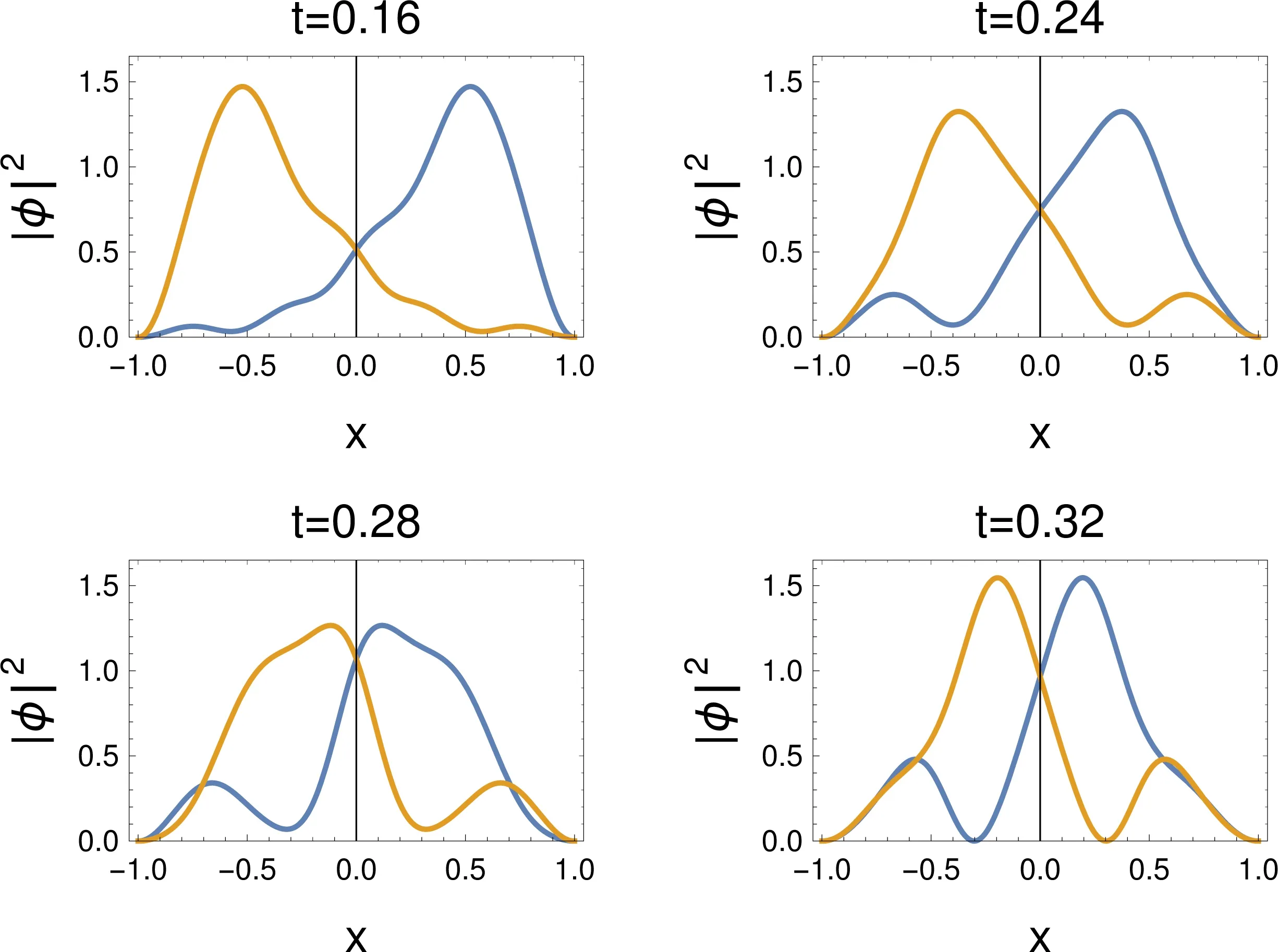
Fig.4 Absolute valueof the squareof the localized orbitals,for a sudden changeof the Ham iltonian.The tim eafter the changeof the Ham iltonian isgiven in atom ic units(1 a.u.≈24 attoseconds),for L=1.
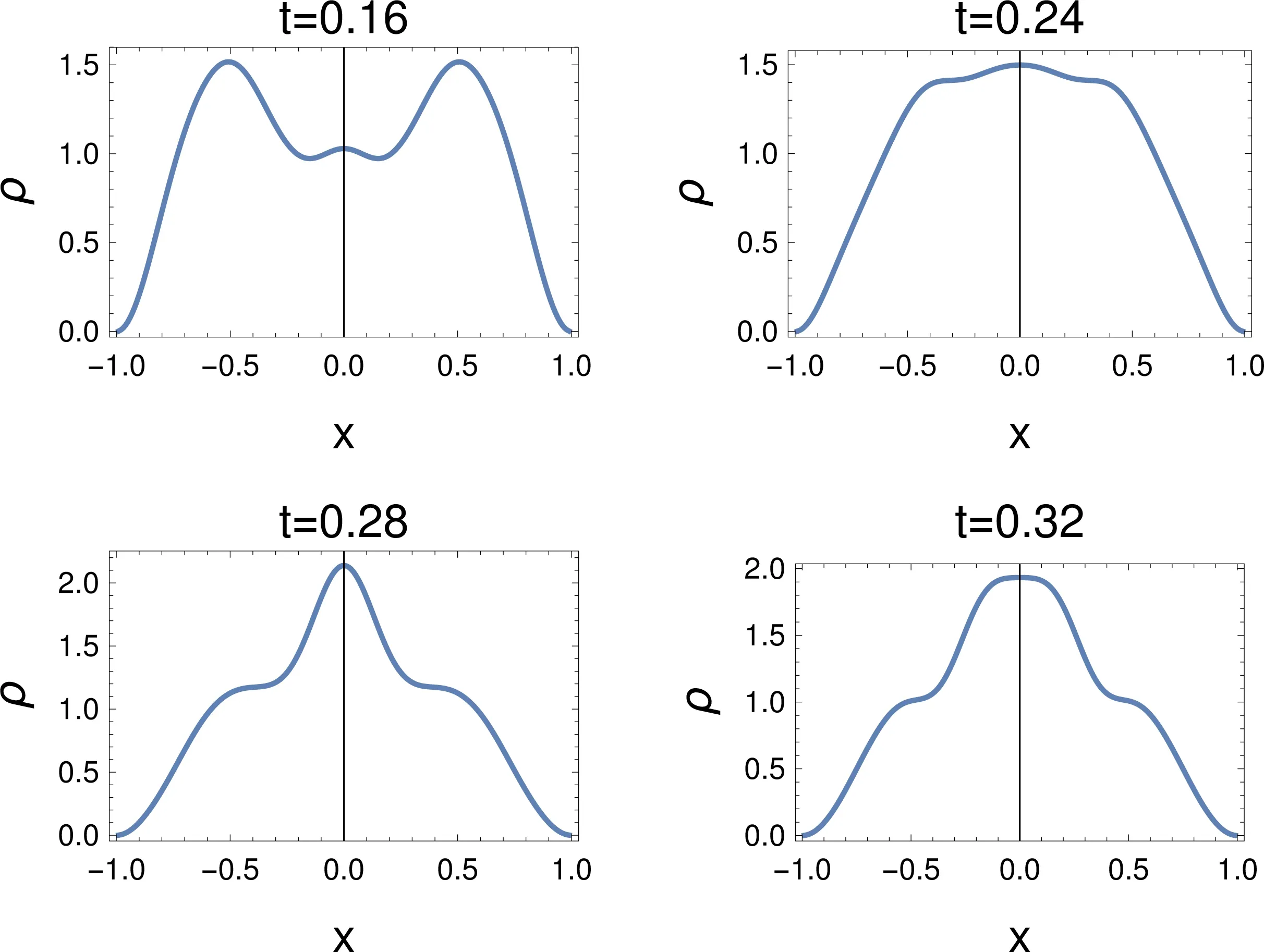
Fig.5 Density,ρ,for a sudden changeof the Ham iltonian.The tim eafter the changeof the Ham iltonian isgiven in atom ic units(1 a.u.≈24 attoseconds),for L=1.
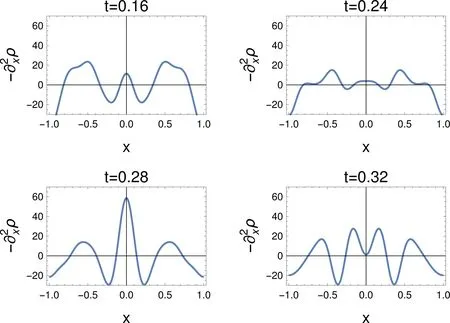
Fig.6 −ρ,for a sudden changeof the Ham iltonian.The tim e after the changeof the Ham iltonian isgiven in atom ic units(1 a.u.≈24 attoseconds),for L=1.
4.2.3 Localized orbitals
Localized orbitals for this process are shown in Fig.4.The orbitalsdelocalizeinto theotherhalf-box(t=0.24).During this process the orbitals getvery close to each other(t=0.28,t=0.32),before reversing themovement,going back to theoriginal half-box,and restarting the cycle.It isworth to remark that in the“unconventional”,intermediatestep(t≈ 0.3),the centroids of chargesof the two localized orbitals getmuch closer than at the start:the localization is only poorly realized.Wew ill later comeback to thispoint.
4.2.4 Density
The change of the density compresseswhat has been seen above,and some information can be lost,cf.Fig.5.At t=0.16 the density presents two importantpeaks,as could be expected,but a new smallmaximum shows up in between.The latter rem inds of the so-called “non-nuclear attractors” that are associated tometallic systems(see,e.g.10,Section E2.1.1).At t=0.24,in accordancew ith the broadmaximum in thewave function,there is a broad maximum in the density.At later times(t=0.28,0.32),the density hasa centralmaximum,and shoulders appear instead of the outer maxima.Plots of the density are notexpected to show such features in the stationary case.
4.2.5 “Lap lacian”of the density
Instead of the Laplacian of the densitywe consideragain,as suited to theone-dimensionalproblem,−.The problems in interpreting the density getmagnified,cf.Fig.6.For example,the smallmaximum in the density at t=0.16 gets sim ilar importance to theother two.At t=0.24 the diあerencebetween maxima fades.At t=0.32,four maxima show up.Should one relate them to the two maxima in each of the localized orbitals?Asw ith the density,one can speculateabouttheorigin of thesemaxima,once we havemore information,but can we interpret−ρ w ithout having it?The problem of having too manymaxima rem indsofoneknown for the CC bond in ethane,see,e.g.10,Section3.2.4).There,although there is justonebond and onewould expecta singlemaximum,the Laplacian of the density shows twomaxima.
4.2.6 Electron localization function
Theelectron localization functionbringsin information thatis consistentw ith the information theψ(x1,x2)gives.Thegraphs show more clearly what is happening than −ρ,as for all t shown,atmost threemaxima show up(see,Fig.7).One is very weak at t=0.16,is weakly distinguishable from the others at t=0.24,while three clearmaxima show up clearly at t=0.28,0.32.However,as for−ρ,it ishard to guesswhat three maximamean,when only two electrons are present,because ELF is used to attribute a domain to each of the electrons(or electron pairs).Know ing that one electron is delocalized over two spatial regions solves the problem.However,one should know that the two basins(on the left,and on the right)have to be grouped together.One could integrate the density over these regions(thesebasins),and get≈3/4 electronsin it.Oneshould note,however,that,oscillations occur(see below),and some further criteria to unify the new ly appeared basinsare needed.
4.2.7 Maximum probability domain
Forinterpretation reasons,themaximum probability domains seem tohave thesimpleststructure.Fig.8 showstheprobabilities tofind one electron between x
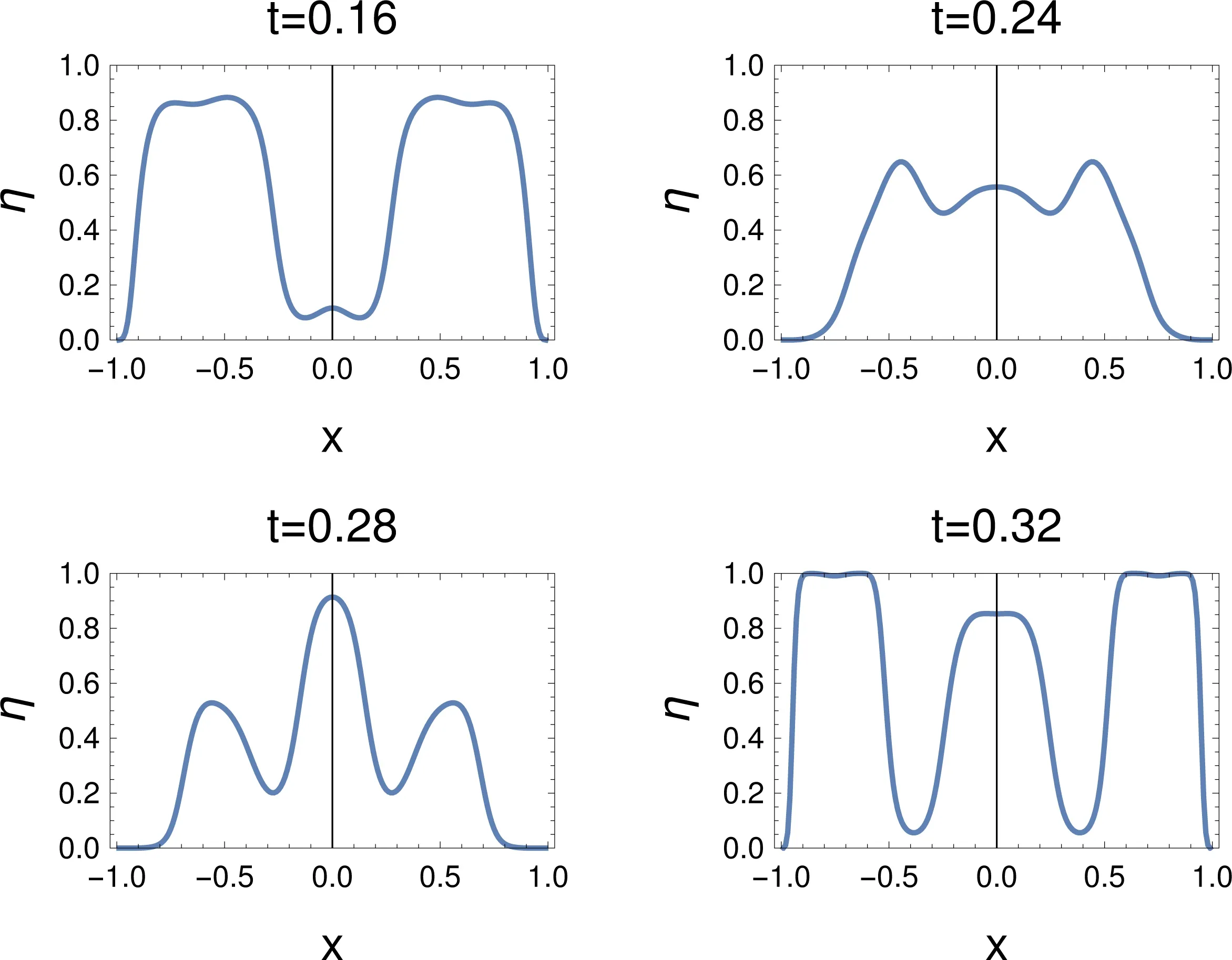
Fig.7 Electron localization function,η,for a sudden changeof the Ham iltonian.The tim eafter the changeof the Ham iltonian is given in atom ic units(1 a.u.≈24 attoseconds),for L=1.
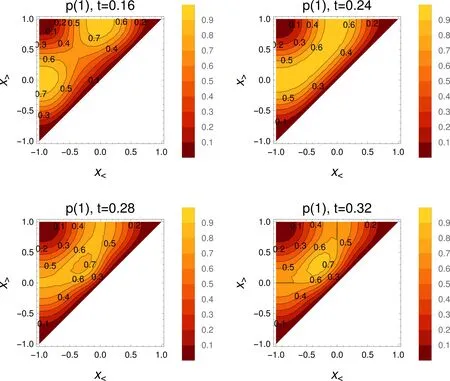
Fig.8 Probability tofind one,and only oneelectron between x
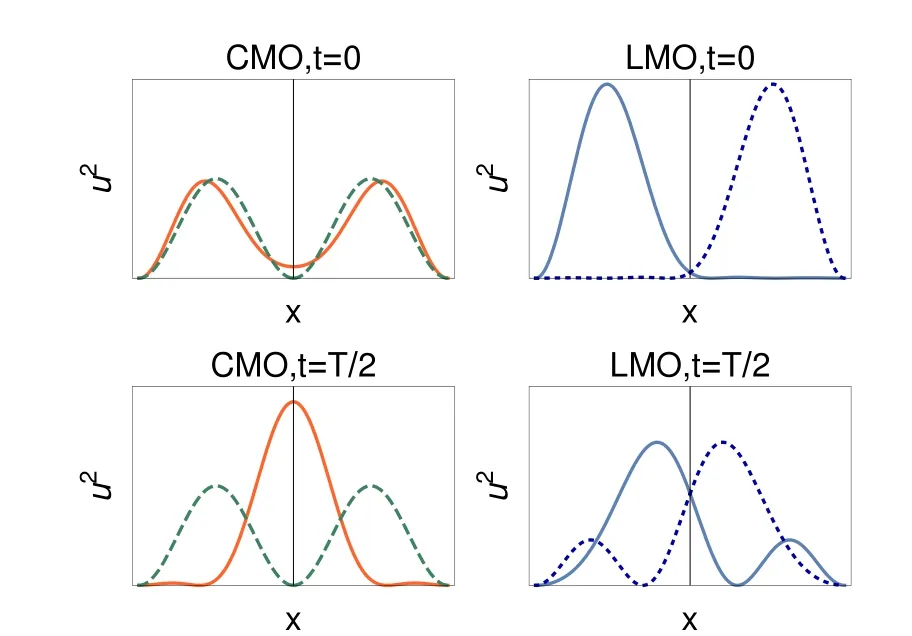
Fig.9 Tim e-dependent orbitalssquared,reduced to the n=1,2components,at tim es t=0,T,...(upper panels),and t=T/2,3T/2,...(lower panels);left for symm etry-adapted orbitals(full lines:u+,dashed lines:u−),right for localized orbitals;sam e scale in allpanels.
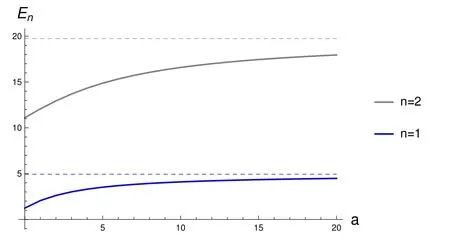
At t= 0.16,the two half-boxes are the maximum probability domains.However,at t=0.24,a diあerence to the adiabatic picture is clear.Forany fixed x 4.2.8 Physical interpretation Eq.(2)is valid when the change of the Hamiltonian is sofast that the wave function does not have the time to change.After the change,the wave functionϕevolvesw ith time,and to 98 percent is amixture of the u+(n=1,a=0,x)and u+(n=2,a=0,x)states(Rabioscillationsare produced): where uk=u+(n=k,x,a=0),ΔE= π2is the diあerence between the energies of the n=2 and n=1 states,c1=8/(3π),c2=8/(5π).Theextreme casesoccurwhen the cosine function equals plus or m inus one,i.e.,at t=jT and t=(j+1/2)T where j isan integernumber,T=2π/ΔE=2/π. Fig.9 shows the squares of the orbitals for times equal to even or for odd numbersof T/2.One notices thatat t=0,the occupied canonical orbitals squared are similar.The diあerence between them comesmainly from the sign in one of the halfboxes.This allows an almost perfect localization by linearly combining the canonicalorbitals.In contrast to it,at t=T/2,the symmetric orbital iswell localized at the center of the box,while theantisymmetricone,u−,isunchanged.The localization obtainedby linearly combining thecanonicalorbitalsispoor:the centroids of the orbitals are close,the delocalization is strong.The total wave functionψ(x1,x2,t=T/2)is given by the Slater determ inant built from ϕ+and u−.It hasmaxima for x1=0,and x2= ±0.5.ψis not shown,as it resembles the one of Fig.3.One can understand it by noticing that u−=0 whereϕ+has amaximum,andϕ+almostvanisheswhere u−hasextrema.Thepictureproduced by the canonicalorbitals(one strongly localized orbital,and one delocalized orbital)is closer to theoneobtained by looking directly to the totalwave function than theone produced by the two poorly localized orbitals. The maximum probability domains do not start from an orbital“prejudice”,but analyze the total wave function.A fter the separating wall has vanished,for certain intervals of time,there is a maximum probability domain around the position where thewallhas been.A lso,by perm itting the spatial region to be spatially disconnected,they allow for the description of the quantum phenomenon that a particle can be found in two diあerentdisconnected domains. 4.2.9 Comparison to stationary states The bestdescription of the chem icalbond is notnecessarily given by a single localized solution even when considering the time-independent case.The simplest example is themolecule,where a localized solution does not exist.Onemay have a localized picture by using resonance structures.In the case of,one can describe itas H...H+↔H+...H.For the system considered in this paper,one can imagine the state at t=T/2 as where◦denotes an unoccupied site.One electron stays at the center,while the other can be either in the left,or in the right half-box.(Of course,as stated before,the single electron↑can be replaced by apair↑↓.The leftor right locationof theelectron pair rem indsof the ionic resonantstateofH2,or thecharge-shift(resonating)bond13.) Another example is given by particles in a ring,ormetals,where the localization is not considered to give the best description.Let us assume that for particles in a ring we have found some region,defined by the points x Onemore example isgiven by atom ic shells.A lthough,e.g.,in an atom like Ne thereare fourelectron pairs,due to spherical symmetry a spatial region defining an electron pair can be oriented in any direction:there are infinitely many equivalent“pair domains”.In this case,we consider atom ic shells,and only destroying the symmetry fixes the orientation of the pairs. Itisworth to stress thatin the time-dependentcase discussed in this paper,it is not the symmetry that produces equivalent solutions,but them ixingw ith excited eigenstates thatgenerates diあerent localization patterns. Interestingly,Lew is4had the intuition of the failure of taking hismodel rigidly.Although desiring to explain polarity,and not the quantum eあects discussed here,he w rites about“tautomerism,where two ormore forms of themolecule pass readily into one another and exist together in a condition of mobileequilibrium”. 4.2.10 Period of the cycle For L=1,the symmetric orbitalϕ+changesw ith a period T≈0.64 atom ic units,or≈15 attoseconds.Thismainly due to the separation between the two lowest energy levels,E(n=1,a=0),and E(n=2,a=0),of the symmetric states u+.As E(k,a=0,L)=E(k,a=0,L=1)/L2,the time evolution for L /= 1 is easily recovered via the transformation t → tL2.The diあerence between E(n=2,a=0)and E(n=1,a=0)thatdeterm ines the period of the oscillations,is unrealistically large for L=1(≈10 hartree).This can be corrected by choosing a larger box.For example,by choosing L=10,it is brought down to≈0.1 hartree,or≈ 3 eV.This way,the period of the cycle is of 1.5 fem toseconds. 4.2.11 Spatialoscillations Up to now,an important technical detail was hidden from the discussion,viz.,the number of functions u+(k,x,a=0)used in Eq.(2).As the process analyzed above is determined mainly by the two lowest energy symmetric states,the figures were produced by limiting the sum to k≤5.We can analyze the eあect of increasing the number of functions,e.g.,up to k=10.ELF,and evenmore importantly−∂2xρemphasize the rapid oscillations produced by adding these higher frequency components.These rapid oscillations producemany maxima,and this makes any analysis based on counting the maxima useless.However,almostno eあect is seen on the probabilities.This can be understood by the need of taking derivatives for obtaining −∂2xρ ,while integration used for generating the probabilitieshasa smoothing eあect. 4.3.1 Mathematicaldescription Up to now,we have obtained results in two lim iting cases.Wewould like to know whether the sudden approximationmay be relevant.For this,letusconsiderexpand the time-dependent,spatially symmetricwave function as After substitution ofφ+into the time-dependent Schrödinger equation,and projection onχm(x),wehave where the dot above the letter represents the derivative w ith respect to t. Detailson solving thisequation aregiven in Appendix D. In contrast to the treatmentbefore,we cannotstartat t=∞,because we would need infinite time tofollow the evolution.Furthermore,wehave to decideabouthow theopacity parameter a changesw ith time.a is uniform ly sw itched oあfrom a large value,inτ≈10 fem toseconds.For t>τ,theHamiltoniandoes notchangew ith timeanymore,but thewave function continues toevolveaccording to theSchrödingerequation,havingasinitial wave function φ+(τ,x).Detailson thechoiceof theparameters can be found in Appendix C. 4.3.2 Probability evolution If the change of the opacity parameter a w ith timewere very slow,one would see essentially the same images as in Fig.2.However,for the choice of the parameters just described,the results look sim ilar to thosegiven for thesudden approximation.It is thusnotnecessary to show and analyze in detail the results again.The calculation has only shown that the regime of the sudden approximation isnotunrealistic. Nevertheless,we discuss how the probabilities evolve w ith time(see Fig.10).One of the curves corresponds to the probability of finding one electron in a half-box.The other,to that of finding one electron in the center(equal to that of finding one electron in the disconnected domain thatexcludes this central region).In Fig.10,when follow ing the evolution in the central region,x<= −x>was arbitrarily set to a time-independent constant.The optimization of x<,x>increases the probability,andmovesup the curve in the figure. Although the probability tofind a centralMPD is not large at themomentτ,when the Hamiltonian hasarrived at the final form,one notices that the probabilities continues to change in time,w ith periods of≈ 64 a.u.(≈ 1.5 fem toseconds).Furthermore,the variation w ith time is important.For≈1/6 of the cycle,around the the probability of finding one electron in the central region is larger than that of finding one in a half-box.The duration where the two probabilities are comparable isevenmore important. Fig.10 Probability tofind one,and only oneelectron in a half-box(between x<=0 and x>=L),dashed curve,and that for x<=0.3L and x>=0.3L(full curve),asa function of tim e after the Ham iltonian stopped changing(given in atom ic units,1 a.u.≈24 attoseconds;for L=10,and the thewallm ade transparent inτ≈10 fem toseconds). The example of two electronsw ith the same spin shows that when the Ham iltonian changes electron localizationmay look,for certain time intervals,qualitatively diあerent from what the adiabatic picture presents.In our example,the latter follows that of Lew is,while time dependence brings in quantum delocalization eあects.It gives a significant probability of finding an electron in two spatially disconnected regions. An analogue to the spatially disconnected regions exists for thewave function solving the stationary Schrödinger equation,e.g.,when resonant structures are needed to describe the bonding.It can be speculated that phenomena like this play a role,e.g.,in charge transfer,in transport properties,also in nano and biologicalsystems. One should not forget that two particles in a box w ith an opaquewall do not represent reality,and thatno choice of the parameters of themodel can compensate for it.However,the simplicity of themodelallows us to look at thewave function,and understand betterhow well,orhow badly,the interpretation toolswork.Thus,the paper has only two objectives,namely to encourage •the study of time-dependent processes,as they disclose unexpected situations for chemicalbond description,and •theuseof themaximum probability domains thatseem well suited for such time-dependentprocesses. We finallymention that latter isclose towhatisalready used in time-dependentcontext,see,e.g.14,and that lim itationsof ELF in time-dependentcaseshasalso been noted before5. Thispaper is dedicated to DebashisMukherjee,who reached his seventies birthday.During themany years of our friendship wespenta long timeindiscussionsonvarioussubjects,including thatof the presentpaper. Append ix A So lu tions of the stationary Sch rödinger equation fo r a partic le in a box w ith an opaque wall As given in Ref.2(problems 19,20),the expressions of the one-particle wave functions,solutions of the stationary Schrödinger equation w ith potential v(x)given in Eq.(1),are given by where k(n,a,L)is the solution of k(n,a,L)cot[k(n,a,L)L]=−a lying between(n − 1/2)π/L and nπ/L.The normalization constant is Fig.11 Eigenvaluesof the stationary Schrödinger equation for a particle in a box w ith awallhaving an opacity increasingw ith a;for n=1,2;those corresponding to the symmetric eigen functions u+are shown w ith fu ll lines;thoseof theantisymm etric eigen functions u−do not depend on a and are shown as horizontaldashed lines. B The exp ression of the elec tron localization func tion for a sing le Slater determ inant Aswe are discussing one-dimensional systems,the formula of ELF is slightly diあerent from thatgenerally used.A lso,we consider the fully polarized systems,while usually the closed-shell formula is given.We follow the initial choice of the interpretation of ELF11,viz.related to the curvature of the Ferm i hole.It also includes the current contribution15,as needed when orbitals are complex,as is the case in time-dependent theory12.For a single Slater determ inant,the explicitexpression of ELF is C Connec ting the opacity param eter a w ith tim e In order to associate time to the opacity parameter a,letus fi rstdefine the rangeof theopacity parameter,a,takes.Wewant to reach afinal=0 starting from a large ainitial=a(t=0)in a timeτ.Forsimplicity,weassumea lineardependenceon time We can define a constantυ=˙a(t)=ainitial/τ.We see that ainitial= ∞is not an acceptable choice if we wantτto be finite.We now choose ainitialsuch that the particles in the two half-boxesare just in contact,i.e.,the density isof the order of 0.001 atomic units.Thisvaluewas taken to delimit the shapeof themolecules(cf.10,Section 1.1).For a size of the box given by L=10 bohr,chosen to give a reasonable fi rstexcited state,thisgives ainitial≈40 atomic units. We have the freedom to chooseτ.For Fig.10,υ =0.1,i.e.,τ=400 atomic units≈ 10 fem toseconds. D So lving the tim e-dependen t Sch röd inger equation In order to solve Eq.(5)abasishas to be chosen.Thebasis is given by the functions that correspond to the symmetric eigenfunctions u+at a=0.Thesystem ofdiあerentialequationswassolved numericallyw ith Mathematica16. Theexpansion in a fixed basis iscomplicated by the presence of the time-dependent cusp in u+(x=0),as shown in Fig.1.However,thisdoesnotseem toaあectthediscussionof theresults. Re ferences (1) Messiah,A.Quantum Mechanics;North Holland Publishing Company:Amsterdam,The Netherlands,1967. (2) Flügge,S.PracticalQuantum Mechanics;Springer:Berlin,Germany,1999;p.14. (3) W igner,E.Phys.Rev.1934,46,1002.doi:10.1103/PhysRev.46.1002 (4) Lewis,G.N.J.Am.Chem.Soc.1916,38,762.doi:10.1021/ja02261a002 (5) Durrant,T.R.;Hodgson,M.J.P.;Ramsden,J.D.;Godby,R.W.arXiv 2015,1505.07687. (6) Artmann,K.Z.Naturforschg.1946,1,426. (7) Scemama,A.;Caあarel,M.;Savin,A.J.Comput.Chem.2007,28,442.doi:10.1002/jcc.20526 (8) Lüchow,A.;Petz,R.J.Comput.Chem.2011,32,2619.doi:10.1002/jcc.21841 (9) Savin,A.ReviewsofModern Quantum Chemistry:ACelebration of the ContributionsofRobertG.Parr;Sen,K.D.Ed.;World Scientific:Singapore,2002;p.43. (10) Bader,R.F.W.AtomsinMolecules:AQuantum Theory;Oxford University Press:Oxford,UK,1990. (11) Becke,A.D.;Edgecombe,K.E.J.Chem.Phys.1990,92,5397.doi:10.1063/1.458517 (12) Burnus,T.;Marques,M.A.L.;Gross,E.K.U.Phys.Rev.A 2005,71,010501.doi:10.1103/PhysRevA.71.010501 (13) Sini,G.;Maitre,P.;Hiberty,P.C.;Shaik,S.S.J.Mol.Struct.THEOCHEM 1991,229,163. (14) Petersilka,M.;Gross,E.Laser Physics1999,9,1. (15) Dobson,J.F.J.Chem.Phys.1993,98,8870.doi:10.1063/1.464444 (16) Wolfram,S.Mathematica Edition,Version 11.1;Wolfram Research,Inc.:Champaign,Illinois,USA,2017.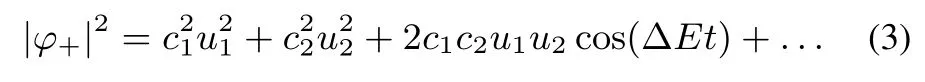
4.3 Exp licit so lu tion of the tim e-dependen t Sch rödinger equation



5 Perspectives
6 Ded ication