双缝干涉测量超声波声速

骆 敏，骆泽如，余观夏，林杨帆

(1.南京林业大学 物理教学实验中心，江苏 南京 210037；2.南京市第一中学，江苏 南京 210001)

声波是在弹性媒质中传播的机械纵波，频率大于20kHz的声波称为超声波. 目前声速测量一般采用驻波法和相位法[1-3]. 声波的波长、频率和传播速度是声波的基本特征量. 双缝干涉实验是验证波动性的经典实验，利用双缝干涉原理测量声速的波长，进而求出声速. 该方法扩展了声速测量的研究途径和方法，深化了学生对波动学规律和基本概念的理解.

1 双缝干涉实验原理

双缝干涉原理如图1所示，缝宽为a,双缝间距d=a+b,对于不同的θ角，干涉极大产生的条件是双缝到屏的波程差等于波长的整数倍，产生干涉极小的条件为波程差等于半波长的奇数倍，即

dsinθ=±kλ,

(1)

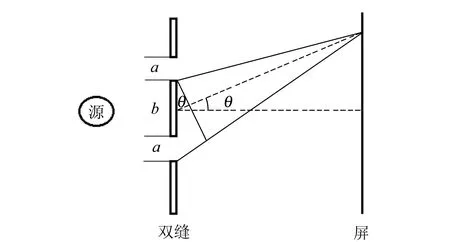
图1 双缝干涉原理图

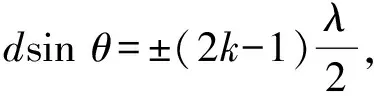
(2)

式中k=0,1,…,n.

2 实验装置和测量方法

2.1 实验装置

实验装置如图2所示，由超声接收换能器、发射换能器、双游标读数转盘、超声信号源，双踪示波器组成. 双缝的缝宽[4-5]为4.00 mm，双缝间距为24.00 mm.

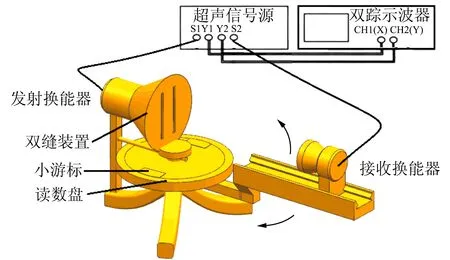
图2 实验装置图

2.2 测量方法

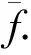
2)测量双缝干涉极大和干涉极小对应的角度θmax和θmin. 转动接收换能器，通过示波器观察正弦波形振幅的变化，当转动到左边的第一极值时(如图3所示)，记录读数盘上2个小游标对应的读数，左边小游标读数为θ1，右边小游标读数为θ2；当转动到右边的第一极值时(如图4所示)，记录读数盘上2个小游标对应的读数，左边小游标读数为θ1′，右边小游标读数为θ2′. 则干涉极大和干涉极小对应的角度为

(3)

图3 双缝干涉左边极值波形图

图4 双缝干涉右边极值波形图

3 实验数据和结果

3.1 谐振频率测量

谐振频率f测量值如表1所示.

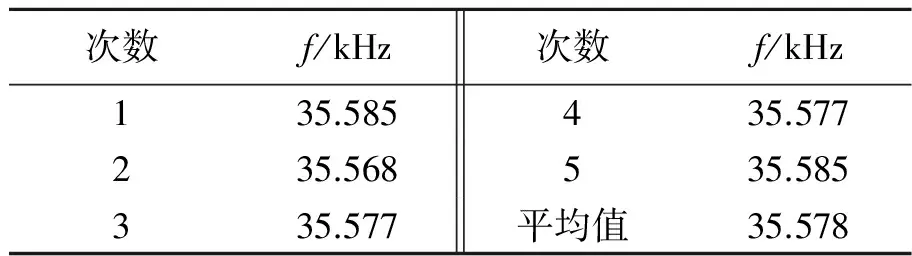
表1 谐振频率测量值

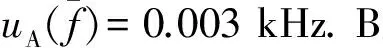
3.2 第一级干涉极小和极大的角度测量

第一级干涉极小角度测量结果如表2所示.

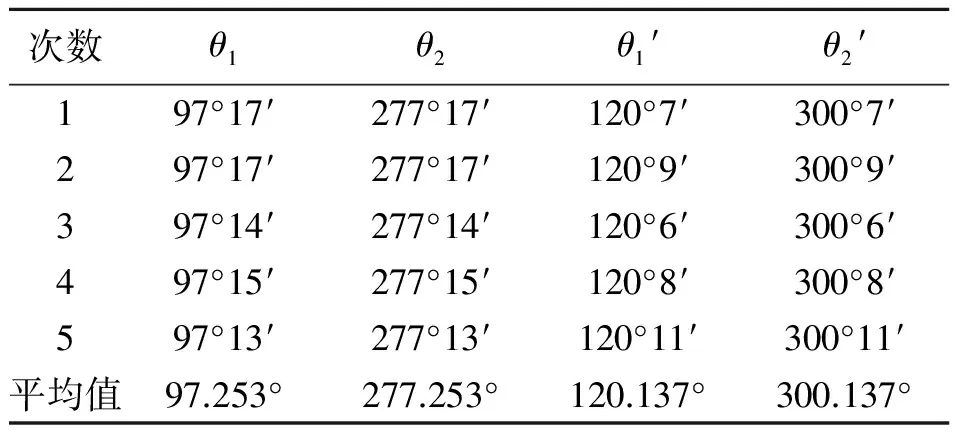
表2 第一级干涉极小角度测量结果

由(3)式得

θmin=11.442°±0.007°.

第一级干涉极大角度测量结果如表3所示.

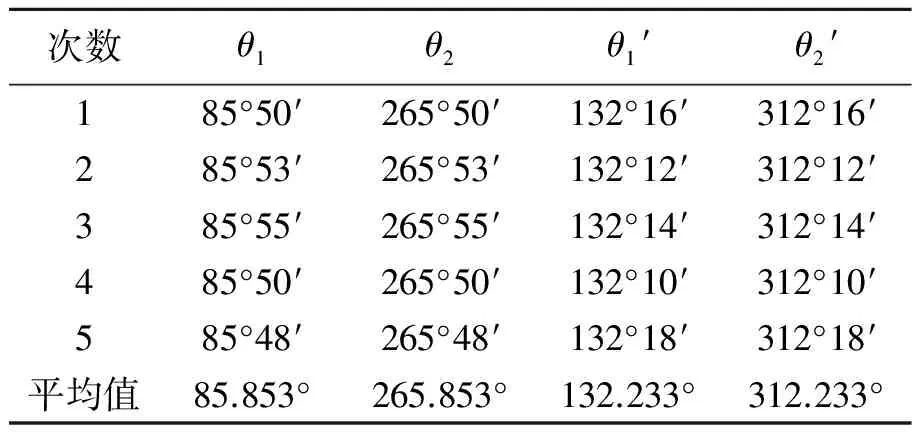
表3 第一级干涉极大角度测量结果

同上可得干涉极大对应角θmax为

θmax=23.190°±0.012°.

3.3 声速的计算

由v=λf，结合式(1)～(2)可得到

v1=fdsinθmax，v2=2fdsinθmin,

代入数据可得

v1=336.239 m/s,v2=338.775 m/s,

进而求得声速的不确定度为[7]

u(v1)=0.334 m/s,u(v2)=0.206 m/s.

因此，测量结果为

v1=(336.2±0.3) m/s,

v2=(338.8±0.2) m/s.

4 实验结果影响因素

1)干涉极大和干涉极小位置具有一定的宽度(角度范围)，在这个角度范围内，示波器的图形都显示极大或极小，所以在记录左右两边(k=±1)的干涉极大或干涉极小对应的角度时，就会产生一定的偏差，这是由实验操作者及系统特有的误差，这种误差不能消除，只可尽可能地减小.

2)声源的发射面积和接收器的面积[8-9]对测量结果也具有一定的影响.

3)声波在介质中传播时，受到吸收、散射等因素的影响，会发生能量的损耗，导致示波器接收波形振幅不稳定而产生微小误差.

4)声速和温度有关，环境温度的稳定性也会给实验测量结果带来一定的误差.

5 结束语

本文提出了不同于运用相位法和驻波法测量声速的方法，方法简单易行，数据测量可靠. 相对应于传统的声速测量方法，叠加的声波的形式复杂，学生不易掌握和理解，而双缝干涉法测量原理和操作简单，可视度好，更有利于学生对波的干涉特性的理解.

参考文献：

[1] 邵维科,赵霞,轩植华. 驻波法测量声速实验的探讨[J]. 物理实验，2017，37(3):48-51.

[2] 花添雨,封维忠,孙成忠. 基于AD8302的相位差法测声速[J]. 物理实验，2017，37(8):10-13.

[3] 周曼. 大学物理实验[M]. 北京:中国农业出版社,2010:112-115.

[4] 张怀广. 双缝衍射缝宽与条纹的关系[J]. 安阳师范学报，1999(2):62-63.

[5] 刘复合. 缝宽及缝间距对双缝干涉衍射条纹的影响[J]. 黑龙江教育学院学报，1995(2):23-23.

[6] 刘勇,张建国,张盛源. 超声波测量声速实验中谐振频率的确定[J]. 高等函授学报(自然科学版)，2012,25(4):75-77.

[7] 朱鹤年. 物理实验研究[M]. 北京: 清华大学出版社,1997:219-233.

[8] 王世平. 光源宽带与干涉条纹可见度的关系[J]. 山东大学学报(理学版)，2005,40(5):85-87.

[9] 吕永生. 光源宽带对干涉条纹可见度的影响[J]. 滁州学院学报，2005(5):94-96.