基于频率配置和解耦率的某风力发电机悬置系统优化
2018-05-25伍保华胡伟辉
伍保华,胡伟辉,岳 涛
(株洲时代新材料科技股份有限公司,湖南 株洲 412000)
0 引言
风能是一种最具有大范围开发和商业化发展前景的洁净可再生能源[1]。风力发电机组是风能利用的核心装备,在双馈型风电机组中,齿轮箱变速机构高速轴通过联轴器和发电机相连接,当机组正常发电时,发电机不可避免地会产生振动和噪声,这些噪声和振动会降低风力发电机组零部件的使用寿命,甚至会造成风机零部件提前失效,影响机组正常运行[2-3]。因此,设计合理的风力发电机悬置系统,减少发电机振动向机架的传递是风力发电机悬置系统研究的重要课题。本文建立某风力发电机悬置系统模型,综合考虑发电机悬置系统固有频率配置和各阶主振动方向的解耦率,优化风力发电机悬置系统刚度参数,并通过实验验证了该优化方法的有效与可行性。
1 悬置系统动力学模型、激励分析与能量法解耦
风力发电机组中,主机架振动远小于发电机振动,发电机的激励频率远小于发电机本身结构频率,因此可将机架和发电机结构本身视为刚体,弹性支撑可以简化为与几何中心三向正交的弹簧阻尼元件[4]。如图1所示,发电机悬置系统采用四点平置式支撑,以发电机质心建立悬置系统坐标系O-XYZ,X轴平行于发电机主轴方向,Z轴垂直于地面,Y轴由右手定位法则确定。A、B、C、D分别表示四个弹性支撑,悬置系统上的点有沿着X、Y、Z轴平动和绕X、Y、Z轴转动6个自由度,即x=[xyzθxθyθz]T。根据拉格朗日方程[5]:
(1)
其中:x为系统广义坐标;T为系统动能;R为系统损耗能量;V为系统弹性势能;F为作用在悬置系统上的广义力矩阵。推导悬置系统六自由度动力学方程为:

(2)
其中:M为系统质量矩阵;C为系统阻尼矩阵;K为系统刚度矩阵。根据动力学方程(2),可以求得系统各个方向的固有频率[6]。

图1 发电机弹性支撑各坐标方向示意图
与传统电动机、发动机不同,发电机主要靠外部输入转矩带动转子切割磁感线发电。发电机主要激励来自于齿轮箱高速轴输入转矩引起的反转矩的波动、发电机转子不平衡质量引起的离心力激励,以及在风机运行过程中紧急制动偏航等极端恶劣条件引起的涡激振动等。因此可以得出发电机主要激励为沿Y、Z轴发电机转子不平衡质量引起的离心力Fz、Fy和绕X轴输入转矩波动Mx。悬置系统激励力F的矩阵表达式为:
F=[0FyFzMx0 0]T.
(3)
根据式(3),在风力发电机悬置系统振动控制中,应重点针对绕X轴和沿Z轴、沿Y轴方向的振动进行控制。
实际运行中,发电机悬置系统的六个自由度是互相耦合的,即六个自由度的运动都不是独立的,某个振动方向多存在一联耦合,引起系统共振的概率就会提高,耦合还会导致系统相邻两阶固有频率重叠,增大振幅,因此,降低重要振动方向的耦合率是十分重要的。能量法是求解系统耦合率的重要方法,系统第i阶固有频率振动时,分布到第k个广义坐标上的能量占系统总能量的百分比Tik为[7]:
(4)
其中:M(k,j)为系统质量矩阵M的第k行j列元素;φ(k,i)、φ(j,i)分别为第i阶振型的第k、j个元素。当第k到第i阶模态自由度完全解耦时,则Tik=100%,发电机悬置系统设计应尽可能提高系统解耦率Tik。
2 风力发电机悬置系统优化建模
2.1 悬置系统优化目标函数
悬置系统目标函数应以系统固有频率合理配置和各个自由度方向高解耦率为目标。在系统设计时,应重点关注悬置系统固有频率配置,然后尽可能地提高系统解耦率,因此要建立各阶固有频率达到最优频率和系统解耦率最大化的多目标函数。合理配置固有频率就是先设定系统各阶频率的最佳频率,频率配置的目标函数为:
(5)
其中:i为固有频率阶数;ωi为系统第i阶固有频率;ωopt为系统第i阶设置的最优频率;α1i为加权因子,在绕X轴和沿Z轴、沿Y轴方向加权因子取3,其余取1。
从提高解耦率方面,可以构造目标函数:
(6)
其中:i、k均为固有频率阶数;α2i为加权因子,在绕X轴和沿Z轴、沿Y轴方向加权因子取3,其余取1。
2.2 设计变量
发电机悬置系统隔振性能、解耦率与系统固有频率和各阶振型、弹性支撑安装位置有关。由于风机空间尺寸的限制,一般采用将弹性支撑布置在发电机底部的形式,弹性支撑安装位置一般在发电机制造过程中已经确定,而发电机型号一旦选定,其惯性参数便已经确定,因此,设计变量应重点从弹性支撑动刚度考虑。为方便弹性支撑加工制造,设定悬置系统4个弹性支撑型号相同,将弹性支撑三向动态刚度kx、ky、kz作为设计变量。
2.3 约束条件
2.3.1 位移约束
为了保证弹性支撑达到设计规定的寿命,弹性支撑在工作时,位移不能太大,刚度不宜过小,设定弹性支撑垂向位移在±5 mm以内、横向位移在±3 mm以内。
2.3.2 频率约束
3 优化实例分析
3.1 风力发电机悬置系统初始状况
以某2 MW风力发电机为例,采用相同的弹性支撑布置在发电机底部,发电机惯性参数如表1所示。

表1 发电机及弹性支撑参数
在ADAMS中建立六自由度悬置系统虚拟样机模型,如图2所示,可利用ADAMS/vibration或者公式(2)和公式(4)得出系统的固有频率和能量坐标解耦率,见表2。表2中,X、Y、Z为沿坐标系轴X、Y、Z平移振动,Rx、Ry、Rz依次为绕坐标轴X、Y、Z的扭转振动。

图2 发电机悬置系统虚拟样机模型
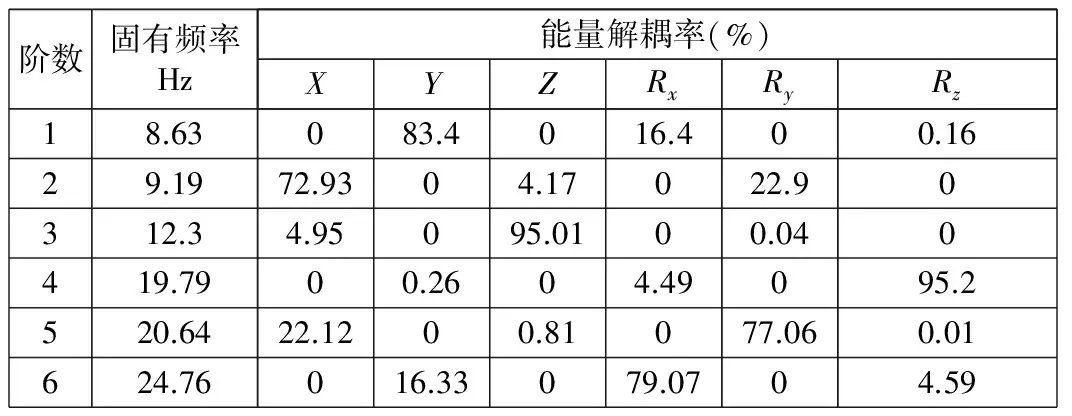
阶数固有频率Hz能量解耦率(%)XYZRxRyRz18.63083.4016.400.1629.1972.9304.17022.90312.34.95095.0100.040419.7900.2604.49095.2520.6422.1200.81077.060.01624.76016.33079.0704.59
由模态分析结果可以知道:该发电机悬置系统初始刚度不合理,发电机激振频率为23.3 Hz~30 Hz,重要方向固有频率已经落在激振范围内,在发电机主要的激励方向沿Y轴、Z轴和绕X轴方向上,对应主振型能量解耦率分布为83.4%、95.01%、79.07%。因此,系统频率需重新配置,沿Y轴和绕X轴能量解耦率也需提高。
3.2 悬置系统模型优化
根据前面分析可知:发电机悬置系统固有频率应小于16.6 Hz才能起到减振效果,设定目标函数F1在重要方向X转动、Y向、Z向最优频率ωopt分别为5 Hz~16.6 Hz的任意数值,目标函数F2设定在重要方向绕X转动、Y向、Z向方向要求为85%以上。利用ADAMS/vibration对悬置系统初始模型进行优化。优化后系统弹性支撑X、Y向刚度为4 kN/mm,Z向刚度为8 kN/mm。其固有频率和能量解耦率见表3。
将优化前、后数据进行对比分析,优化后悬置系统频率得到了合理的配置,最大固有频率为16.2 Hz,满足了频率配置要求。另外,在重要激励方向绕X转动、Y向、Z向能量解耦率均达到了90%,其余方向解耦率均在85%以上,系统解耦得到了很大改善。

表3 优化后悬置系统各个坐标上的能量解耦率与各阶频率
4 试验验证
为进一步验证优化后参数的有效性,本文进行了发电机-弹性支撑系统振动测试实验,见图3。通过振动测试仪测出不同转速下发电机轴承驱动端部的速度响应。优化前、后悬置系统驱动轴承端部Y向、X向、Z向速度响应曲线对比分别如图4所示。

图3 某发电机悬置系统振动测试
从图4中可以看出:当发电机处于低转速(1 300 r/min)运行时,优化前、后悬置系统驱动端轴承三向振动速度均小于2 mm/s,幅度较小;当发电机转速大于1 300 r/min,优化后悬置系统驱动端轴承三向振动速度明显得到改善,特别是Y向,最大振动速度由8 mm/s降低至2 mm/s以内,效果明显,进一步验证了上述优化过程的正确性。
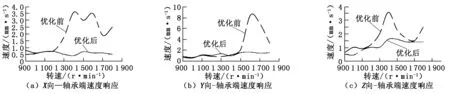
图4 优化前、后悬置系统驱动端轴承速度响应
5 结论
(1) 建立了发电机-弹性支撑悬置系统刚体动力学模型,对悬置系统激励特性进行了详细分析。确定了主要方向的激励力,同时建立了系统能量解耦方程,为悬置系统仿真和优化设计奠定了理论基础。
(2) 建立了以频率和解耦率为目标的悬置系统优化设计模型,对某风力发电机悬置系统进行了优化设计,改善了系统的频率配置,提高了系统解耦率。
(3) 对改善前后的某发电机悬置系统进行系统驱动轴承端的速度响应对比测试,测试结果表明优化后悬置系统隔振性能得到了提高。
参考文献:
[1] 苏竣眭,纪刚.中国政府资助的可再生能源技术创新[J].中国软科学,2008(11):34-44.
[2] 刘建勋,胡伟辉,林胜,等.双馈式风力发电机减振系统的优化[J].噪声与振动控制,2011(3):29-31.
[3] 张登峰,郝伟.风力发电机组的振动测试与诊断[J].大电机技术,2012(1):10-13.
[4] 时培成.汽车动力总成悬置系统隔振分析与优化研究[D].合肥:合肥工业大学,2010:1-5.
[5] 王峰.汽车动力总成悬置系统振动分析及优化设计[D].上海:上海交通大学,2008:1-10.
[6] 屈维德,唐恒铃.机械振动手册[M].北京:机械工业出版社,2000.
[7] 吴飞,胡朝辉,成艾国,等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化[J].汽车工程,2013,35(1):18-22.
