基于遗传算法的冲压车间节能调度优化研究

0 引言

节能减排是当今制造业面临的普遍问题，实施低碳制造的发展战略在世界各国已达成共识。目前，实现制造业的低碳和节能已成为研究的热点。冲压成形是金属加工行业中的重要组成部分，是机械制造业的基础行业，我国制造业所用的钢材，有60%～70%是板材，其中大部分用于冲压加工[1]。同时，由于在金属加工行业中冲压成形能量消耗相对较大，因此，对冲压成形加工开展低碳节能的研究具有重要的现实意义。

为了实现可持续发展，在考虑生产效率的同时降低生产能耗是其重要的一个方面。实际生产中，调度是影响制造业效率、成本、质量的关键因素，不同的调度方案会对企业生产过程中的资源和能源的消耗产生影响，因此在保证效率、成本、质量的同时，还需要合理分配工件在不同设备上加工，最大限度的降低生产过程中的能耗。目前已有不少学者对冲压车间的生产调度进行了研究，但主要侧重于传统的调度目标研究（时间、成本等）而没有考虑能耗对环境及成本的影响。如2004年常剑峰[2,3]等人通过建立虚拟制造系统，对冲压线进行了虚拟计划和调度的研究。2005年张晓东[4]等人针对焊装和涂装等车间的集成调度优化问题，提出了多级车间的集成优化模型，并设计遗传启发混合算法求解该模型。2009年李峥峰[5]等人根据冲压车间生产的无等待并行流水作业特点，建立了基于启发式规则的双向冲压生产线调度模型，并设计了嵌入启发式规则的混合遗传算法来进行求解，使得最大完工时间最小。2012年徐兵[6]等人针对实际冲压生产中缓存区与机器冲突问题，建立了模型并将等待时间作为启发因子利用混合蚁群遗传算法对其进行求解使其生产成本最小。2017年Sayak Roychowdhury[7]等人针对汽车冲压车间，提出了基于启发式的遗传算法，利用该算法优化使得最大完工时间最小，最后证明该算法要优于遗传算法。

此外，近年来不少学者对节能调度优化做了大量研究，但主要侧重在机加工车间，成形车间的研究仍不足。如2014年Fadi Shrouf[8]等人基于实时电价，建立了调度模型并利用遗传算法优化使之生产过程中能耗成本最小，结果表明通过避免能源价格较高的时间段可以大幅度降低能源成本。2015年Wenwen Lin[9]等人利用基于教与学的多目标优化算法优化车削加工调度使得最大完工时间和碳排放最小，此外采用了三种碳足迹减排策略通过减少机器的空闲时间和搜索空间大大改善了优化结果的性能。2016年何彦[10]等人针对机械车间任务柔性工艺路线对机械车间调度能耗的影响特性，提出一种面向机械车间柔性工艺路线的节能调度方法并建立了节能调度模型，以加工总能耗、加工完成时间、机床负载为目标采用改进的Q学习算法对模型进行求解获得其Pareto解。

本文通过分析某企业的冲压生产车间的实际情况，对其冲压过程中的能耗特性进行详细研究，并建立多目标节能调度优化模型，该模型可以通过优化工序与机器的选择获得最优的生产调度方案，以达到节约加工总能耗。该模型的优化目标包括最大完工时间（TC）、加工总成本（CT）和加工总能耗（ET），并采用基于多层编码的遗传算法进行求解。最后通过案例研究，验证了建立的优化模型和设计的求解算法能够有效解决冲压车间调度问题并可获得更加节能的生产调度方案，同时能够在保证最大完工时间和加工总成本的前提下节约加工总能耗。

1 冲压车间多目标节能调度模型

1.1 模型描述

常见的生产调度模型一般有两种：作业车间调度模型与流水作业车间调度模型，冲压车间属于作业车间，但因其生产特殊性，它有很多类似流水车间的特性[11]。在冲压车间的生产调度中，冲压车间的生产计划一般是将具有不同批量的n种不同种类的冲压件安排到m台冲压机组成的生产线上进行冲压，不同工序有不同的可选设备集，具有一定的柔性。同一种类的冲压件工序数和每道工序的加工时间、成本和能耗已知，但不同种类的冲压机工序数各不相同。

由于冲压车间生产的冲压件种类众多，各冲压设备的型号不同，每个冲压件的工艺数不一，而且其加工路径具有较高的柔性，所以在时间、成本和能耗较优的情况下，为冲压件选择合理的冲压机进行加工，显得尤为复杂。目前不少学者对冲压车间生产调度问题进行了研究，但考虑尚不够全面或研究目标未包含能耗。本文的研究是针对不同种类不同批量的冲压件在冲压生产线上的调度，使其最大完工时间，加工总成本和加工总能耗最优。

在建立冲压车间多目标节能调度优化模型时，必须考虑以下基本条件：

1）每个冲压件的加工工序及在每道工序上的加工时间、成本和加工能耗已知；

2）每道工序有多台设备可供选择并且已知；

3）不同批次冲压件工序之间没有先后约束，同一批次冲压件工序之间有先后约束；

4）开始加工之前，冲压件的批量、型号和工序数都是已知的且都可以被加工；

5）某一种冲压件的某个工序不能同时在多台冲压件上加工；

6）同一批次冲压件在同一时间只能加工一道工序；

7）同一批不同冲压件之间的空载时间都计入加工时间。

1.2 冲压过程的能耗特性分布曲线

冲压成形过程根据压力机设备的状态分为快下、压制、快上和空载四个状态，不同状态的能耗特征不同，一般压力机加工时的状态能耗特性分布曲线如图1所示。

图1 设备能耗特性曲线

图1是在满负荷下加工某工序的能耗特性分布曲线图，根据实际测量多数工序能耗特性分布情况可知，压制过程所需能耗远小于满负荷情况下所需能耗，冲压机与工序分配不协调，导致有用功比例过小、能量利用率低，在完成最终加工任务的基础上，若希望加工总能耗越小，必须通过合理的调度优化，使得不同批次的工序选择合适的冲压机进行加工。

1.3 模型构建

1.3.1 参数定义及约束条件

假设某冲压车间在一定生产周期内计划生产n种不同冲压件，有m台冲压机供生产使用，在冲压车间内，由于各个时间都会安排不同类型的冲压件生产，每种类型的冲压件都有着不同的工序路线和工序数，在能耗、成本和最大完工时间约束条件下，建立冲压生产车间能耗调度模型，相关参数如表1所示。

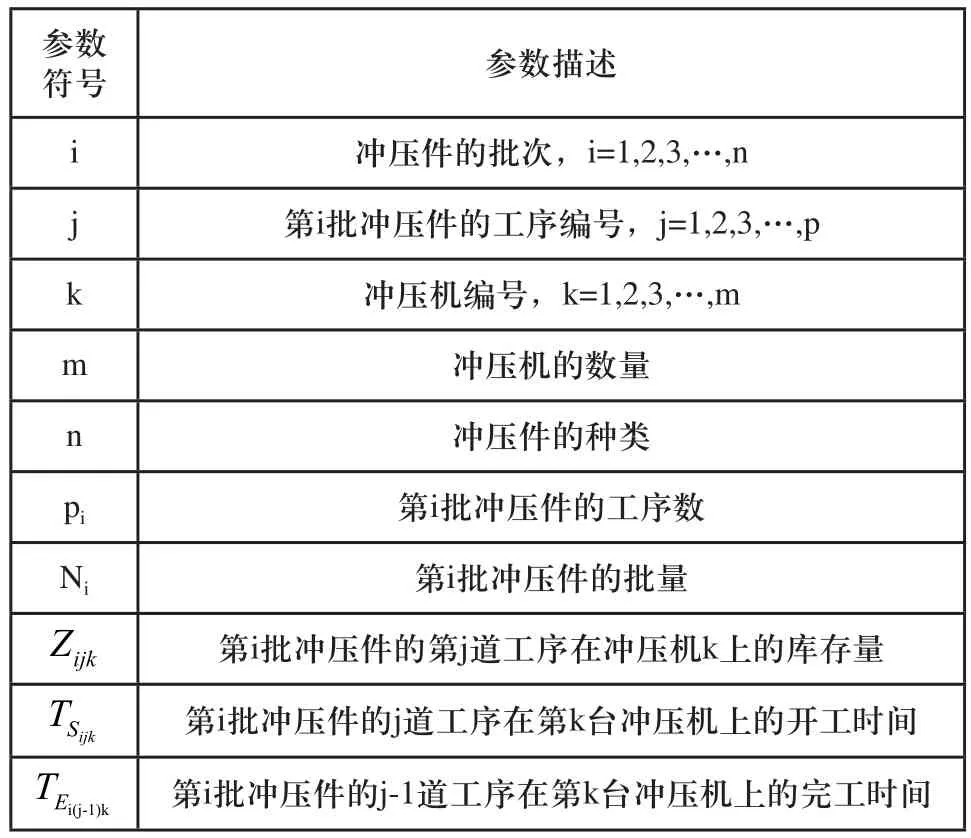
表1 模型相关参数符号及描述

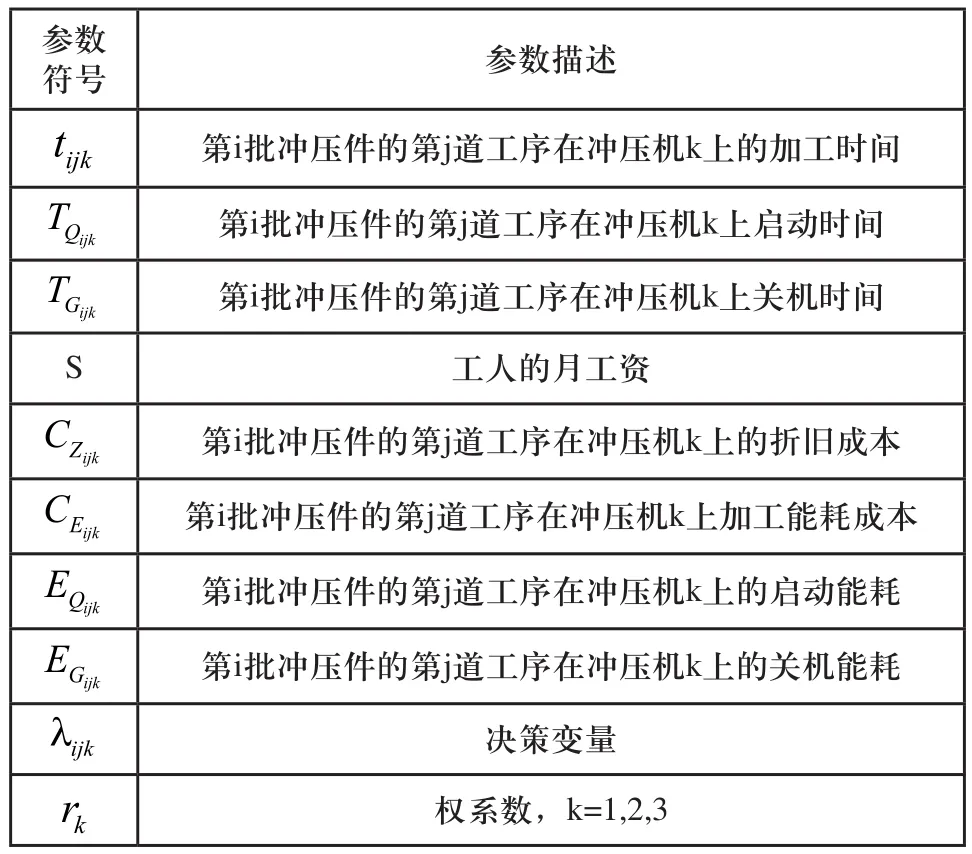
续（表1）

在有限约束条件情况下，本模型主要考虑以下三个方面的约束：

1）资源约束

在一个生产周期内，对于同一批次冲压件而言，不能同时在不同冲压机上加工，对于冲压机而言，不能同时加工不同工序，约束如下：

2）工序约束

在一个生产周期内，不同冲压件工序之间不存在约束，但同一冲压件各工序之间存在先后约束，约束如下：

式(1)表示第i批冲压件的j道工序在第k台冲压机上的开工时间-第i批冲压件的j-1道工序在第k台冲压机上的完工时间≥0。

3）库存约束

在一个生产周期内，同一冲压件的某一工序在某一设备上的库存量小于等于该冲压件的批量。

式(2)表示冲压件i的第j道工序在设备k上的库存量小于等于冲压件i的批量。

1.3.2 目标函数建立

在冲压车间调度研究中，大多数学者主要以考虑完工时间、设备负载率和生产成本为主，根据不同的生产情况，考虑的目标不尽相同。本文从节能角度出发，基于某企业冲压生产车间的实际生产情况，以最小化最大完工时间、加工总成本和加工总能耗为目标分别建立如下优化函数。

1）最小化最大完工时间：

2）最小化加工总成本

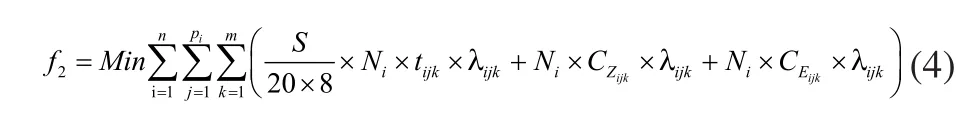
3）加工总能耗最小

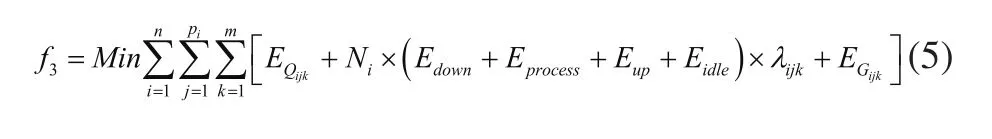
式(5)中Edown、Eproess、Eup和Eidle分别表示第i批冲压件第j道工序在冲压机k上的快下能耗、压制能耗，快上能耗和空闲能耗。

1.3.3 模型的多目标处理

由于上述模型存在三个目标函数，属于多目标决策模型。一般情况下，多目标优化模型不存在最优解，而将存在的最优解称为非劣解。求解非劣解最常用的方法是线性加权法[12]。

根据某企业生产实际情况确定三个优化目标的权重rk，即TC、ET、CT的权重rT、rE、rC分别为0.3,0.5,0.2。并采用以下公式计算各个体的适应度值（Fi），最后以Fi为目标进行最优化求解，即对Fi进行选择、交叉和变异操作。

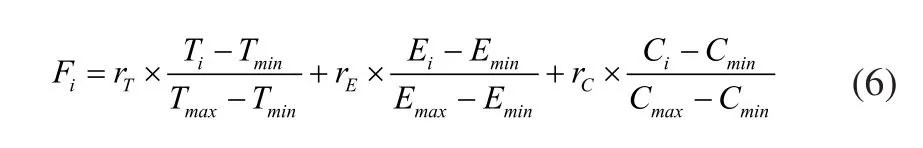
式(6)中Tmax、Tmin，Emax、Emin，Cmax、Cmin分别表示单目标优化时最大完工时间，加工总能耗和加工总成本可行解的最大值与最小值。

2 冲压车间节能调度模型的算法实现

自从1985年，Davis[13]首次将遗传算法引入生产调度算法以来，在生产调度研究领域获得广泛的应用并取得较好的效果。将遗传算法用于作业车间调度问题的关键是采用有效的编码和解码方式以及适当的交叉、变异操作，对种群重复地进行选择、交叉、变异等基本遗传操作，不断产生出比父代更适应环境的新一代种群，直到满足要求条件为止[14]。其基本流程如图2所示。针对作业车间调度问题用遗传算法求解已有不少研究[15～17]，目前编码普遍采用基于工序的编码方式，为了有效地解决柔性作业车间不同工序有不同可选设备集的问题，本文的编码方式采用双层编码，即前半部分表示工件的加工工序，后半部分表示对应的加工机器。

图2 遗传算法流程图

2.1 个体的编码

染色体编码方式为整数编码，每一个染色体表示全部冲压件的加工顺序，当待加工的冲压件种类为n，冲压件的批次为i，第i批冲压件的工序数为pi，则染色体个体长度为其中，染色体的前半部分表示所有冲压件在冲压机上的加工顺序，后半部分表示冲压件每道工序的加工冲压机编号，如图3所示。

图3 基于工序和机器的双层编码

图3的编码表示加工工序分别为4,2,3,3的四种冲压件在七台冲压机上加工时的编码。

2.2 适应度值计算

单目标优化时，染色体的适应度值分别为最大完工时间（TC）、加工总成本（CT）、加工总能耗（ET）。多目标优化时，染色体的适应度值为式(6)的Fi。

2.3 选择操作

选择操作采用轮盘赌法选择法，其基本思想是各个个体被选中的概率与其适应度大小成正比，具体操作如下：

1）计算出种群中每个个体的适应度Fi（i=1，2，…，M），M为群体大小；

2）计算出每个个体被遗传到下一代群体中的概率；

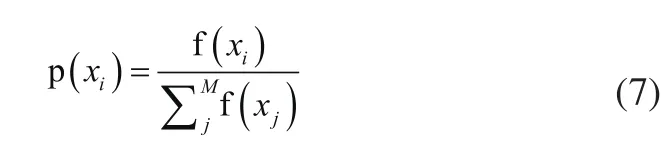
3）计算出每个个体的累积概率；

qi称为染色体xi（i=1，2，…，n）的累积概率；

4）在[0,1]区间内产生一个均匀分布的伪随机数r；

5）若则选择个体1，否则，选择个体σ，使得成立；

6）重复4）、5）共M次。

2.4 交叉操作

种群通过交叉操作获得新的染色体，从而推动整个种群的进化，本文采用整数交叉法，首先从种群中随机取两个个体，并取出每个染色体的前位，然后随机选择交叉位置进行交叉操作，操作方法如图4所示，交叉位置为6。

图4 交叉操作

交叉后某些工件的工序多余，如个体1中的工件2的第一道工序和第二道工序，某些工件的工序缺失，如个体1中的工件1和工件3的第一道工序，因此把工件工序多余操作变为工件工序缺失的操作，并按交叉前个体的操作机器来调整个体到为如图5所示。

图5 调整操作

2.5 变异操作

种群通过变异操作获得新的个体，从而推动整个种群进化。变异算子首先从种群中随机选取变异个体，然后选择变异位置pos1和pos2，最后把个体中pos1和pos2位的加工工序和与之对应的加工机器编号对换，如图6所示，交叉位置为1和5。

图6 变异操作

3 案例研究

为验证节能调度优化模型和求解算法的可行性及有效性，选取某企业冲压车间加工一批包含四种冲压件（内燃机罩体、筋板、围板、水箱盖板）的任务进行调度试验研究，四种冲压件的工序和批量如表2所示，车间所含冲压机吨位信息如表3所示，各批冲压件的各工序加工时间TCi、成本CPi和能耗EPi信息如表4所示。遗传算法参数设置为：个体数目NNID=40，最大遗传代数MAXGEN=100，交叉率XVOR=0.9，变异率MUTR=0.1。

为了验证基于工序和机器多层编码的柔性冲压车间节能调度优化模型的有效性及优势，设定了基于MATLAB的4种案例进行仿真试验，案例1为考虑优化目标为最大完工时间（TC）的单目标调度。案例2为考虑优化目标为加工总成本（CT）的单目标调度。案例3为考虑优化目标为加工总能耗（ET）的单目标调度。案例4为考虑优化目标为最大完工时间（TC）、加工总成本（CT）和加工总能耗（ET）的多目标调度。

表2 冲压件工序和批量表

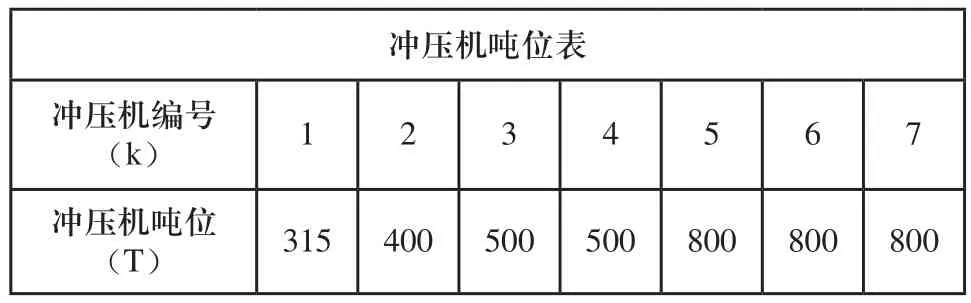
表3 冲压机吨位表

根据第2节建立的调度优化模型和第3节提出的优化算法，可求解出某冲压车间4种冲压件的12道工序在7台冲压机上的生产调度最优化方案，如表5所示。迭代过程中，适应度值Fi的变化如图7所示，随着代数的增加，目标函数的最优值随之不断优化，说明所设计的优化算法具有良好的收敛性。最优化调度方案的甘特图如图8所示。

表4 冲压件各工序的加工时间、成本和能耗

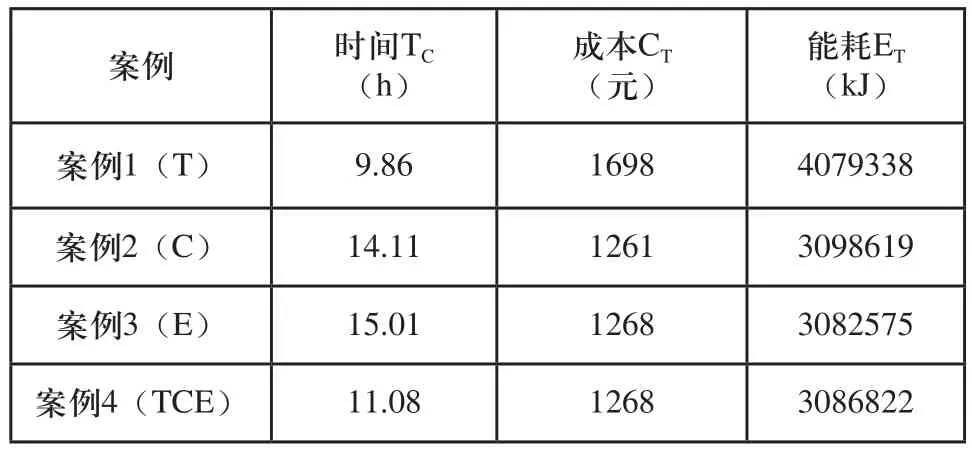
表5 各案例的优化结果

图7 目标函数最优值的进化过程

图8 最优化调度方案甘特图

通过对比分析4种案例的优化结果可知，针对4种不同冲压件的12道工序在7台冲压机上进行加工的生产调度，多目标节能调度（案例4）的最大完工时间要比传统的调度（案例1）增加了12.4%，而相对于案例2和案例3又分别减少了21.5%和26.2%。同时，多目标节能调度的成本要比传统的调度减少了25.3%，但比单目标优化（案例2）的成本增加了0.5%。而多目标节能调度的能耗要比传统的调度减少了24.3%，比单目标优化（案例3）的能耗增加了0.14%，如图9所示。

图9 四种案例的优化结果

由此可见，所设计的基于多层编码的遗传算法在冲压车间的节能调度可在最大完工时间增加较少的情况下，较大程度地降低能耗、减少成本，验证了冲压车间多目标节能调度优化模型的有效性和实用性。

4 结论

1）本文结合某企业冲压车间实际生产过程中设备的能耗特性分布曲线建立了以最大完工时间、加工总成本和加工总能耗为目标的多目标节能调度模型。

2）采用基于多层编码的遗传算法对冲压车间多目标节能调度模型进行求解，得到了最优化调度方案。

3）将多目标节能调度结果与传统的以最大完工时间为目标的调度方案进行对比，证明了所提基于多层编码的遗传算法在冲压车间的节能调度可在最大完工时间增加较少的情况下较大程度地降低能耗、减少成本，验证了冲压车间多目标节能调度模型的有效性和实用性。

通过案例研究的对比分析，冲压车间多目标节能调度优化模型在一定程度上可降低冲压车间加工总能耗，同时使得最大完工时间和成本较优。在金属加工中，冲压成形又是消耗能耗相对较大，所以对冲压成形开展节能调度有着重要的意义。然而本文的案例研究并未考虑辅助能耗和批量划分且调度规模较小，接下来的研究重点将集中于当调度规模不断扩大后，不同求解算法的对比分析以及考虑辅助能耗的调度模型的构建方法研究和基于批量划分的调度。

参考文献：

[1]鄂大辛.成形工艺与模具设计[M].北京:机械工业出版社,2014.

[2]常剑峰,钟约先,韩赞东.轿车车身冲压生产线虚拟制造系统的研究[J].塑性工程学报,2004,11(4):61-66.

[3]常剑峰,钟约先,韩赞东.虚拟环境下汽车冲压车间动态调度的研究[J].塑性工程学报,2004,11(6):84-88.

[4]张晓东,严洪森.多级车间生产计划和调度的集成优化[J].机械工程学报,2005,41(9):98-105.

[5]李峥峰,喻道远,杨超英,等.基于启发规则的双向冲压生产线调度研究[J].华中科技大学学报(自然科学版),2009(6):60-63.

[6]徐兵,李建军.基于混合蚁群遗传算法的冲压生产调度研究[J].计算机工程,2012,38(13):215-217.

[7]Roychowdhury S, Allen T T,Allen N B. A Genetic Algorithm with an Earliest Due Date Encoding for Scheduling Automotive Stamping Operations[J].Computers & Industrial Engineering,2017,105:201-209.

[8]Shrouf F, Ordieres-Meré J,García-Sánchez A, et al. Optimizing the production scheduling of a single machine to minimize total energy consumption costs[J].Journal of Cleaner Production, 2014,67(6):197-207.

[9]Lin W, Yu D Y, Zhang C, et al.A multi-objective teaching learning-based optimization algorithm to scheduling in turning

【】【】processes for minimizing makespan and carbon footprint[J].Journal of Cleaner Production,2015,101:337-347.

[10]何彦,王乐祥,李育锋,等.一种面向机械车间柔性工艺路线的加工任务节能调度方法[J].机械工程学报,2016,52(19):168-179.

[11]王万良,吴启迪.生产调度智能算法及其应用[M].北京:科学出版社,2007.

[12]蒋增强,左乐.低碳策略下的多目标柔性作业车间调度[J].计算机集成制造系统,2015,21(4):1023-1031.

[13]Davis L. Job Shop Scheduling with Genetic Algorithms[A].International Conference on Genetic Algorithms[C].L.Erlbaum Associates Inc.1985:136-140.

[14]周辉仁,郑丕谔,宗蕴,等.基于遗传算法的作业车间调度优化求解方法[J].计算机应用研究,2008,25(10):2991-2994.

[15]Pezzella F, Morganti G,Ciaschetti G. A genetic algorithm for the Flexible Job-shop Scheduling Problem[M].Advanced Research on Computer Science and Information Engineering.Springer Berlin Heidelberg,2011:3202-3212.

[16]Driss I, Mouss K N, Laggoun A. A new genetic algorithm for flexible job-shop scheduling problems[J].Journal of Mechanical Science & Technology,2015,29(3):1273-1281.

[17]赵诗奎,方水良.基于工序编码和邻域搜索策略的遗传算法优化作业车间调度[J].机械工程学报,2013,49(16):160-169.