基于MIDAS-GTS的钢板桩围堰整体抗滑稳定分析

彭 渊 ，于世松 ，刘 刚 ，邓成发 ，刘勇林

（1.浙江省水利河口研究院，浙江 杭州 310020；2.浙江广川工程咨询有限公司，浙江 杭州 310020）

1 问题的提出

浙江省沿海地区软土地基深厚、土质软弱，因此在临江、临海水闸工程建设中，围堰设计的优劣制约着整个工程建设的投资和进度。随着国家海洋战略的实施，水利工程建设由高滩涂对围堰的要求越来越高，传统的围堰如土石围堰、草土围堰、木板桩围堰和木笼围堰，已经不能满足现代工程建设的要求。

随着技术的发展，钢板桩围堰成为最常用的一种围堰型式。钢板桩是带有锁口的一种型钢，其截面有直板形、槽形及Z形等，有各种大小尺寸及联锁形式。常见的有拉尔森式、拉克万纳式等。其优点为：强度高，容易打入坚硬土层；可在深水中施工，必要时加斜支撑成为一个围笼；施工速度快；能按需要组成各种外形的围堰，并可多次重复使用。但目前钢板桩围堰的设计无针对性的规范依据，实际工程多凭经验确定设计参数[1-7]。本文以温州市某钢板桩围堰工程为背景，借助先进的岩土专用软件Midas GTS对实际工程案例进行安全复核，并对围堰进行优化设计。在数值分析过程中，采用渗流 — 应力 — 边坡模块[8]，考虑渗流 — 应力耦合作用，探讨围堰整体稳定安全系数，为钢板桩长度的选取提供参考。

2 工程概况

温州市某拟建钢板桩围堰结构型式见图1。堰宽9.0 m，堰顶高程为5.50 m，外海侧涂面高程为-2.50 m，基坑侧开挖后基底高程为-4.50 m。设计水位为20 a一遇高潮位5.30 m。外海侧钢板桩采用U型热轧钢板桩，桩顶高程为6.80 m。基坑侧钢板桩采用U型冷轧钢板桩，顶高程为6.00 m。采用D2型钢拉杆，布置间距1.4 m。表层地基采用4.0 m厚吹填砂置换，围堰两侧采用抛石镇压，外海侧镇压层长度27.0 m，基坑侧镇压层长度为22.0 m，镇压层一级平台高程为0.00 m，二级平台高程为-1.00 m。

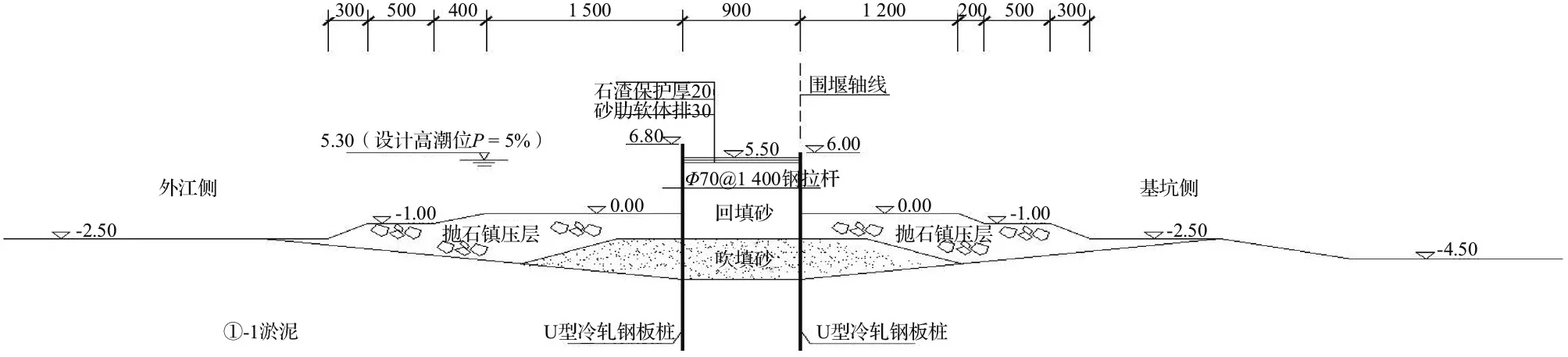
图1 拟建钢板桩围堰典型断面图 单位：cm

钢板桩围堰施工过程为：①地基表层吹填砂置换；②钢板桩打入设计深度；③拉杆、围檩的安装；④钢板桩间回填砂与围堰两侧抛石镇压层交替回填；⑤基坑侧抽水排干[9]。

3 强度折减系数法

目前，研究边坡稳定性的传统方法主要有：极限平衡法、极限分析法、滑移线场法等。这些建立在极限平衡理论基础上的各种稳定性分析方法没有考虑土体内部的应力应变关系，无法分析边坡破坏的发生和发展过程，没有考虑土体与支挡结构的共同作用及其变形协调，在计算安全系数时通常需要假定滑裂面形状为折线、圆弧、对数螺旋线等。而有限单元法不但满足力的平衡条件，而且考虑材料的应力应变关系，使得计算结果更加精确合理。本文引用有限元折减系数法[10]，通过计算发现求得的安全系数大小与程序采用的屈服准则密切相关，不同的准则得出不同的安全系数。π平面上不同α、k的屈服曲线见图2。

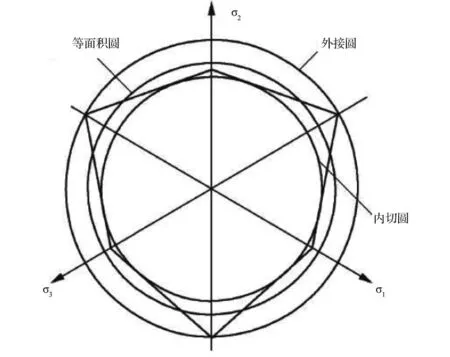
图2 π平面上不同α、k的屈服曲线图

传统的极限平衡法采用莫尔 — 库伦准则，但因莫尔 —库伦准则的屈服面为不规则的六角形截面的角椎体表面，存在尖顶和棱角，给数值计算带来困难。本文采用徐干成、郑颖人（1990）提出的莫尔 — 库伦等面积圆屈服准则代替莫尔 — 库伦准则，并导出各准则间的换算系数η，由此可将求得的安全系数折算成莫尔 — 库伦等面积圆屈服准则下的安全系数[11-12]，不同摩擦角时的的换算系数η见表1。

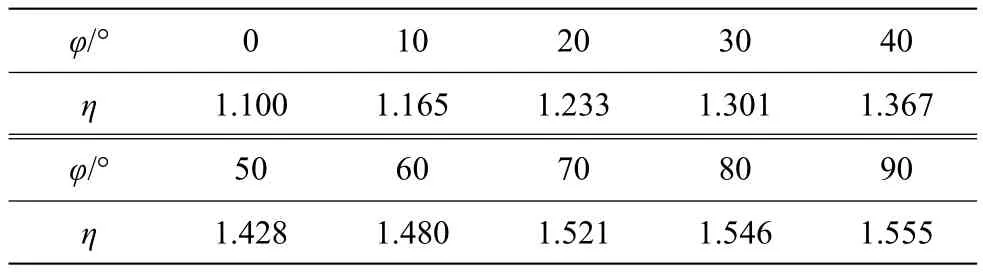
表1 不同摩擦角时的η值

4 有限元计算模型

按照平面应变问题建立模型[13]（见图3 ～ 4）。为控制计算精度并节约计算时间，围堰基本采用四边形平面应变网格划分，围堰及其附近网格采用细密网格划分。钢板桩、钢拉杆设为线弹性模型，弹性模量为210 GPa，泊松比为0.30。根据以往经验，围堰的刚度按复合桩墙的刚度折减50%与实际情况比较吻合，因此将钢板桩的弹性模量取为原来的1/2[14]，即为105 GPa。拉森IV钢板桩设计应力容许值为200 MPa，内支撑采用Q235B钢材，设计应力容许值为145 MPa。土体数值参数见表2。

图3 整体有限元模型图

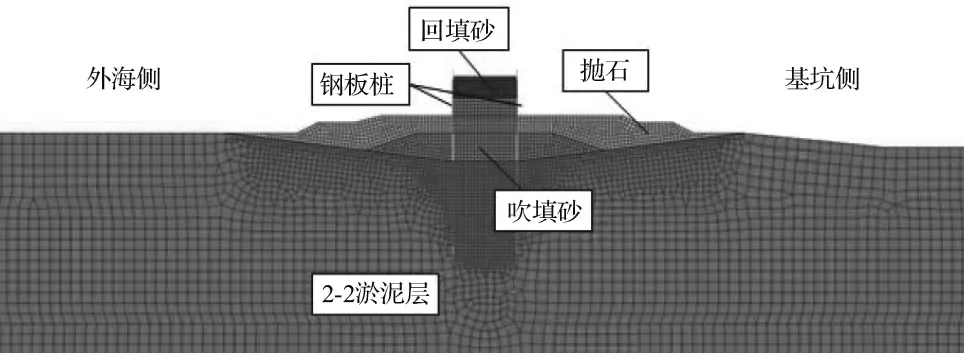
图4 围堰有限元模型图

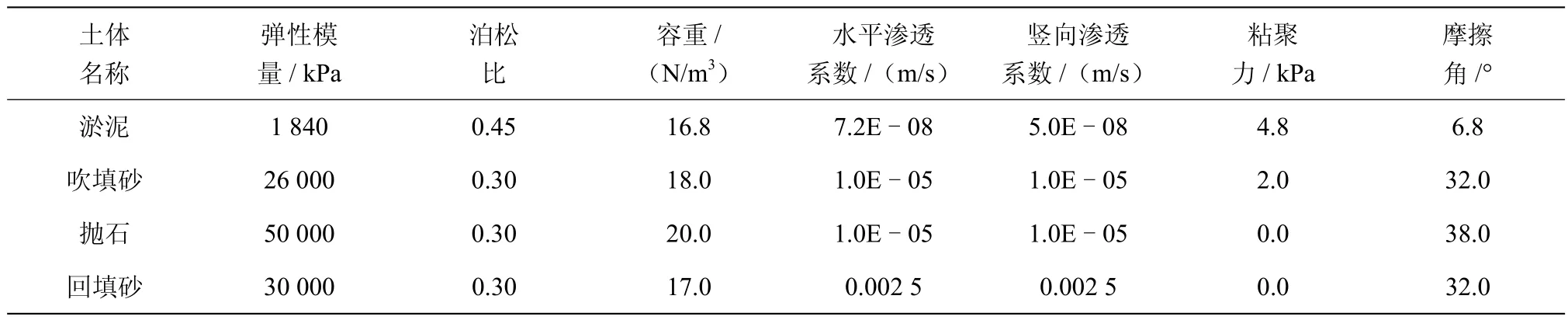
表2 土体数值参数表

考虑到桩土作用的影响范围，板桩围堰左右边缘向两侧延伸150.0 m，土层深度取80.0 m。在模型两侧添加水平约束，底边界添加固定约束，模型上表面为自由边界。外海侧添加8.0 m总水头，基坑侧设置0.0 m总水头。

本次主要针对钢板桩最不利工况进行模拟计算，即外水位为20 a一遇高潮位，基坑内侧施工区域为少水（按无水考虑）的最不利工况。按施工过程分阶段依次加载模拟[15-16]。即初始地应力→吹填砂（第1工序）→钢板桩、钢拉杆（第2工序）→钢板桩内侧回填砂（第3工序、三步回填）→钢板桩外侧抛石（第4工序）→施工区抽水排干（第5工序，外海侧水头8.0 m，基坑侧无水）的过程进行施工步加载模拟。采用Midas GTS特有的渗流 — 应力 — 边坡分析功能，通过模拟不同的钢板桩长度L（L分别取17.0 ，19.0，21.0，23.0，25.0，27.0 m），围堰宽度B = 9.0 m，探讨在堰宽一定的情况下合理的桩长。

5 计算结果

5.1 整体稳定分析

本次钢板桩围堰的整体稳定系数依据SL 645 — 2013《水利水电工程围堰设计规范》6.1.5条规定，采用简化毕肖普法计算时，4、5级围堰的最小稳定安全系数为1.15。

围堰最不利工况整体稳定计算结果见表3及图5。桩长17.0 m时，SRM法计算的稳定系数为1.06，对应的施工区抽水排干工况最危险滑弧面比较明显，滑弧几乎贯串上下游（见图5 a），故不能满足稳定计算要求。桩长增加为19.0 m时，SRM法计算的稳定系数为1.09，下游侧滑弧面明显变淡（见图5 b）。随着桩长的增加，桩长为21.0，23.0，25.0，27.0 m对应的稳定系数分别为1.10、1.14、1.18、1.20。稳定系数与桩长呈非线性的正相关关系。

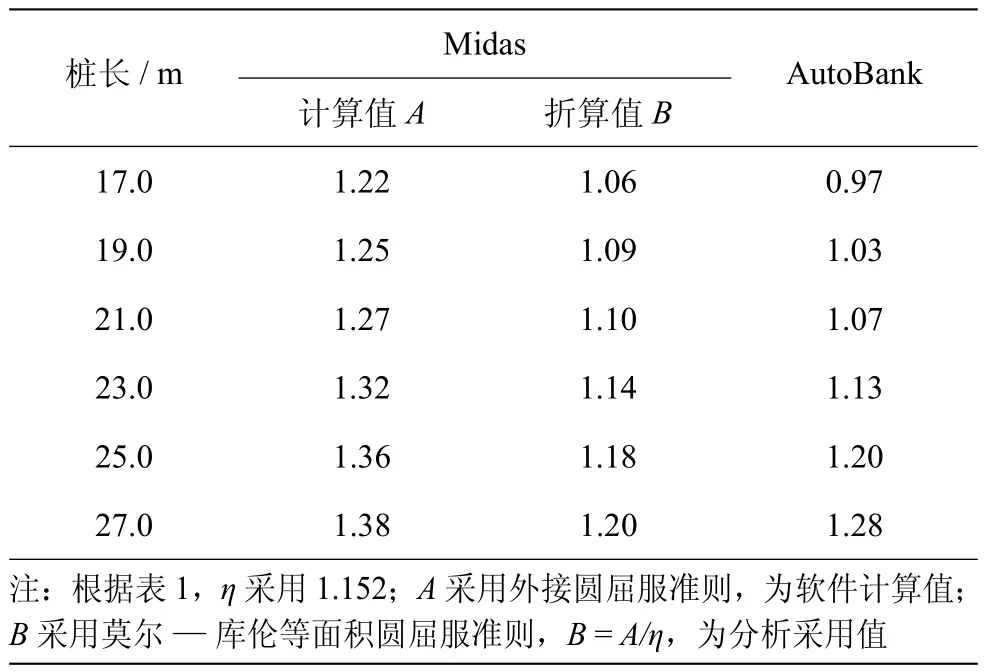
表3 安全系数计算结果表

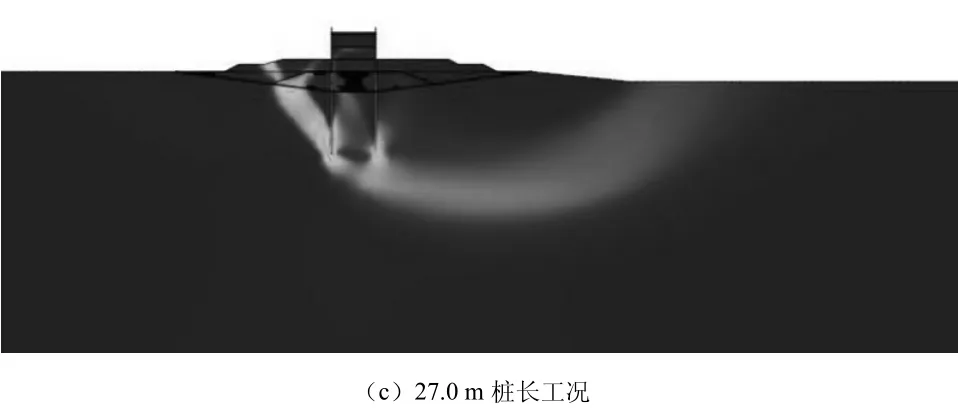
图5 围堰的最危险滑弧面(采用Midas)图

围堰的典型最危险滑弧面见图6。

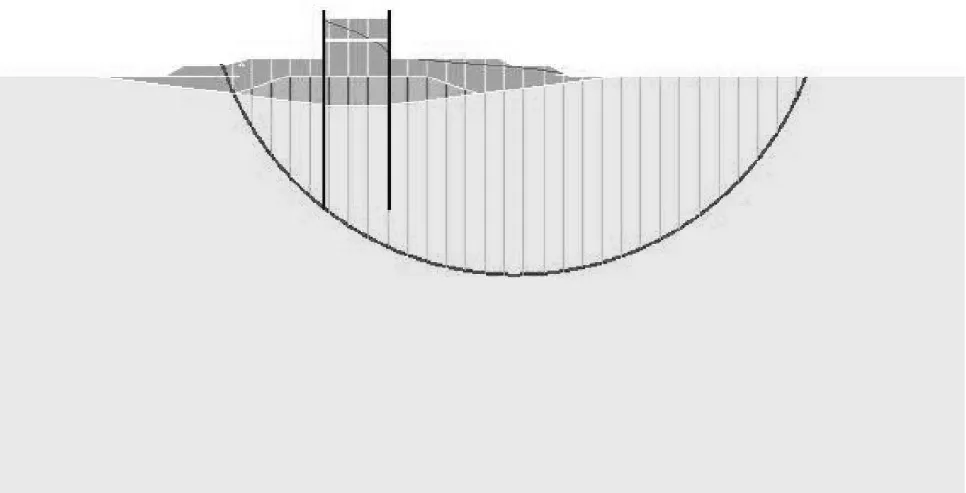
图6 围堰的典型最危险滑弧面 (采用AutoBank) 图

由表3可知，Midas与AutoBank（简化Bishop法）计算的数值结果相近。对比图6可知，2种软件计算的最危险滑弧面位置也相近。

由表3可知，25.0 m桩长的稳定系数为1.18＞1.15，已满足规范要求（经验算，抗倾覆稳定等也满足规范要求）。考虑到工程投资等因素影响，围堰宽度为9.0 m时，推荐采用25.0 m桩长方案。

6 结论与建议

本文以实际工程为基础，采用MIDAS GTS和AutoBank两种软件对钢板桩围堰进行计算，探讨在最不利工况下桩长的变化对围堰整体抗滑稳定的影响，并得到如下结论：

（1）采用Midas GTS与传统的毕肖普法计算结果相近，变化规律一致；钢板桩围堰整体抗滑稳定系数与桩长呈非线性的正相关关系。

（2）整体抗滑稳定分析为钢板桩围堰设计应考虑的一个主要因素。尚需考虑其他安全因素，包括抗倾覆稳定、抗渗透破坏等，计算方法可参照相关规范，本文不再赘述。

参考文献：

[1] 张海通，张红秀.钢板桩施工质量控制[J].人民长江，2000，31(11)：5 - 7.

[2] 孙昕.“U”型钢板桩施工技术分析[J].人民长江，2001，32(1)：21 - 23.

[3] 马明，熊跃飞.钢板桩施工组织设计及技术控制[J].人民长江，2000，31(11)：3 - 4.

[4] 向道明.刚板桩围堰的设计和施工[J].桥梁建设，2003(3)：64 - 66.

[5] 夏颂军.深厚软弱地质条件下钢板桩围堰设计[J].世界桥梁，2016，44(6)：17 - 21.

[6] 姚安军.水利工程中钢板桩围堰施工技术实例[J].黑龙江水利科技，2011，39(6)：46 - 47.

[7] 徐卫军，马水山.长江堤防钢板桩防渗工程安全监测[J].人民长江，2001，32(4)：6 - 9.

[8] 王海涛，易富民，涂兵雄，等.MIDAS/GTS岩土工程数值分析与设计[M].大连：大连理工大学出版社，2015.

[9]张凯.钢板桩围堰应用与受力分析[J].山西建筑，2015，41(4)：180 - 181.

[10] Griffiths D V，Lane P A.Slope stability analysis by finite elements[J].Geotechnique，1999，49(3)：387 - 403.

[11] 郑颖人，赵尚毅，李安洪，等.有限元极限分析法及其在边坡中的应用[M].北京：人民交通出版社，2011.

[12] 赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002，24(3)：343 - 346.

[13] 江杰.船坞双排刚板桩围堰施工工程的数值模拟分析[J].水运工程，2011(8)：24 - 27.

[14] 潘鸿，王加利，曹洪，等.刚板桩围堰在不同施工工序下的变形及内力特性研究[J].岩石力学与工程学报，2013，32(11)：2318.

[15] 杜闯，丁红岩，张浦阳，等.钢板桩围堰有限元分析[J].岩土工程学报，2014，36(2)：159 - 163.

[16] 吴清，尹浩辉.模拟施工过程的官洲河特大桥钢板桩围堰分析计算[J].铁道建筑，2010(5)：8 - 11.