水文测站上下游辅助水位对推流的影响分析
2018-05-25伍远康金辉明
伍远康,金辉明
(浙江省水文局,浙江 杭州 310009)
1 问题的提出
流量作为河道行洪能力大小的直接指标,对洪水预警和防洪调度减灾关系极大。由于流量要素的实时自动监测受到河段条件和测流技术等的制约,只有在为数较少的水文站能够实现。多数水文站只能依靠传统的流速仪渡河方式施测流量,由于其测流时间长、时效性差,难以满足防汛调度和洪水预警的要求。河道流量除由流速仪法实测外,对于水位流量关系单一的水文站,可以根据历年或上年水位流量关系,用本站遥测水位较为准确地推求实时流量,但多数水文站的水位流量关系由于受到洪水涨落、下游水位顶托、河床冲淤变化等的影响,水位流量关系散乱,用本站水位难以满足推流精度要求,对于这一类水文站,能否借助上下游辅助水位进一步提高推流精度。本文以西苕溪港口水文站2015年实测资料为例,分析增加上下游辅助水位在提高推流精度中的作用。
2 港口水文站概况
港口水文站是西苕溪流域控制站,水文站以上控制面积1 970 km2,下游距太湖29 km。西苕溪是浙江北部水系,发源于湖州市安吉县杭垓镇高村,流经赋石水库后由西南向东北经递铺、安城、梅溪后进入平原,至小溪口后分2支,北支经旄儿港,在白雀塘桥汇入长兜港入太湖;南支经西苕溪古道至湖州,汇入东苕溪后,经湖州环城河在白雀塘桥与旄儿港汇合后经长兜港入太湖[1]。西苕溪以梅溪为界,上游为山区性河道,河床坡陡,下游为平原河道,水流平缓。港口水文站以上32 km设有横塘村水文站,上游19 km设有梅溪水位站,下游15 km设有杨家埠水文站,下游18 km设有杭长桥水文站,入湖河口设有小梅口水位站(见图1)。
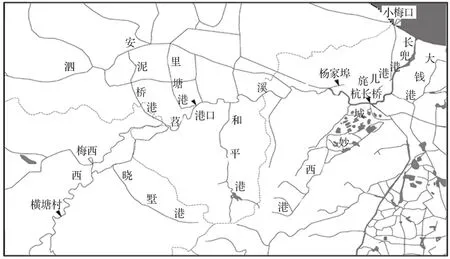
图1 西苕溪水文站点分布图
3 分析思路和方法
港口水文站地处平原河流,受太湖水位、东苕溪来水等复杂因素影响,水位流量关系点据散乱,常年采用连实测流量法推求水文站控制断面月年径流量,要求测次多,测验任务十分繁重。能否利用现有上下游辅助水位,提高港口水文站推流精度,从而减少全年流量测次,本文进行了有益的尝试。分析以港口水文站实测流量为因变量,逐一加入本站和上下游同时水位,建立多站水位与港口站流量的回归推流模型,针对非正态非线性高维数据空间的统计回归问题,引入了投影寻踪回归非线性方法,以推算流量与实测流量之差的方差最小为目标函数,进行模型参数寻优,并对推算流量与实测流量相关关系进行检验。
3.1 投影寻踪回归模型
投影寻踪回归模型(Projection Pursuit Regression简称PPR)[2]是国际统计界于20世纪70年代中期发展起来的新技术,是统计学、应用数学和计算机技术的交叉学科,属于当今前沿领域,用来分析、处理高维观测数据,尤其是非正态非线性高维数据的一种新兴统计方法。通过把高维数据投影到低维子空间上,寻找出能够反映原高维数据结构或特征的投影,以解决高维空间中的回归问题。目前,常用回归方法有线性回归、多项式回归等,但当这些方法用于高维空间时,无法克服随着维数增加计算量成指数倍增长的“维数灾难”问题,投影寻踪回归是解决该问题的有效途径。同时,由于各个预测因子之间存在各种相关关系,其相关关系并不是一致的线性或非线性,因此采用统一的线性或非线性形式建立回归模型不能真实反映流量与水位之间的回归关系。为此,投影寻踪回归方法引入了加权思想,用若干个岭函数加权和的形式来逼近回归函数。投影寻踪回归模型表示为:

式中:m为输入空间维数;p为逼近的子函数个数(个);αk= [αk1,αk2,…αkm]T为m 维空间的第k个投影方向,并要求为观测向量(x1,x2…xm)在第k个投影方向上的投影量;fk为第k个方向上的岭函数,反映了第k个投影量与因变量y之间的关系;βk为权重,表示第k个岭函数fk对输出的贡献大小;ε为残差。为了提高回归计算精度,将计算残差作为因变量,再与观测向量xj建立多元回归方程,回加入式(1),即:
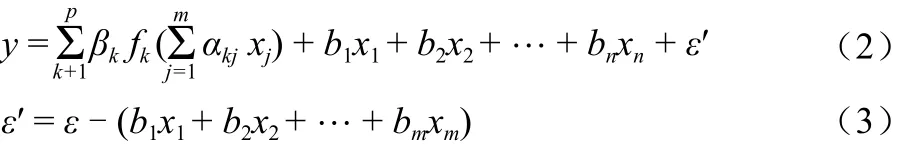
3.2 数据归一化
由于水位、流量在量纲上的差异,会影响数据分析的结果。在建模分析之前需进行归一化处理,将水位、流量化为无量纲的标量,原始变量经过数据归一化处理后,各变量处于同一数量级,便于进行综合对比评价,计算结果再反向还原为原始变量。由于不同的归一化计算方法,会有不同的投影回归计算效果,在分析比较后统一采用偏差变换法,这种方法利用原始变量的均值和标准差进行数据标准化[3]。经过处理的数据符合标准正态分布,转换函数为:

式中:X*为经归一化处理后的新样本(无量纲),X为原有样本,μ为原有样本数据的均值,σ为原有样本数据的标准差(m3/s)。
3.3 参数最优化方法
投影寻踪回归模型的n维参数向量为:

系统的目标函数记为:
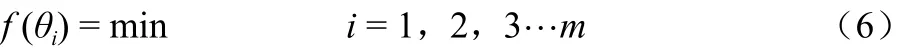
以推算流量与实测流量之差的离差标准差最小为目标函数,采用模式搜索法寻优[4],即假定一个岭函数阶数、最佳投影方向数和遗传种群规模数初值,由该初始点向四周探索,找到一个离差标准差比初始点低得多的方向,就向下前进一步。通过反复这种步骤,总能找到一个离差标准差不能再小的点,该点即为最优点。
4 分析结果
2015年,港口水文站全年用流速仪共测流383次,水位、流量变化范围分别为1.06 ~ 5.30 m和-20.30 ~ 584.00 m3/s,实测水位流量关系见图2,散点明显分布成带状。为了充分利用已有上、下游水位以提高定线推流的精度,以港口站流量为因变量,本站和上、下游水位为自变量,利用投影寻踪回归分析方法建立推流模型推求流量,建模方案见表1。
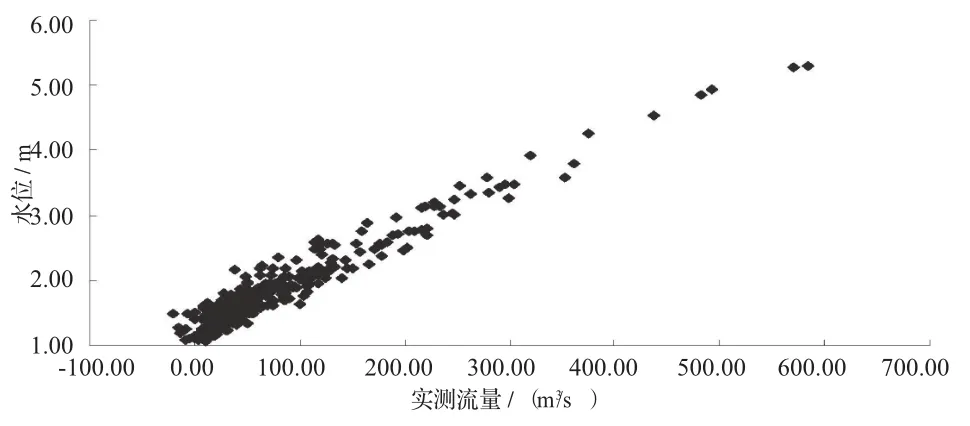
图2 2015年港口水文站水位流量关系图

表1 建模方案表
统计实测流量与计算流量系列的均值、相关系数和离差标准差,并进行符号检验、适线检验和偏离数值检验(见表2),点绘实测流量与推算流量相关图(见图3 ~ 8)。可见,随着上下游水位的逐一加入,相关点据带宽缩小、相关系数增大、离差标准差减小;进一步分析还发现,在港口本站水位流量关系基础上,逐一加入邻近的上下游水位时推流精度提高最为明显,再继续加入上下游更远处水位时,推流精度在统计意义上虽有改进,但并不显著,说明更远处的水位对推流控制断面流量的影响变小。因此,对于受洪水涨落、下游水位顶托等复杂因素影响,水位流量关系散乱的水文站,特别是水面比降较小的平原地区的水文站,只要在水文站上、下游合适位置设置1个或2个辅助水位站,采用本文推荐的方法推流,可以达到减少流量测次,提高推流精度的目标。同时,在本站水位流量关系的基础上,加入上、下游辅助水位,相当于增加了测验河段水面比降因子,更能综合反映河道过水能力的变化。众多影响河流过水能力的因素,如洪水涨落、回水顶托、河床冲淤、水草兴衰、人为分流等也会在水面比降上有所反映,因此,推流关系也会更稳定,这就为类似的水文站借用上一年的推流关系,用遥测水位推求实时流量,实现流量自动监测和预警提供了可能。

表2 各方案推流精度统计表
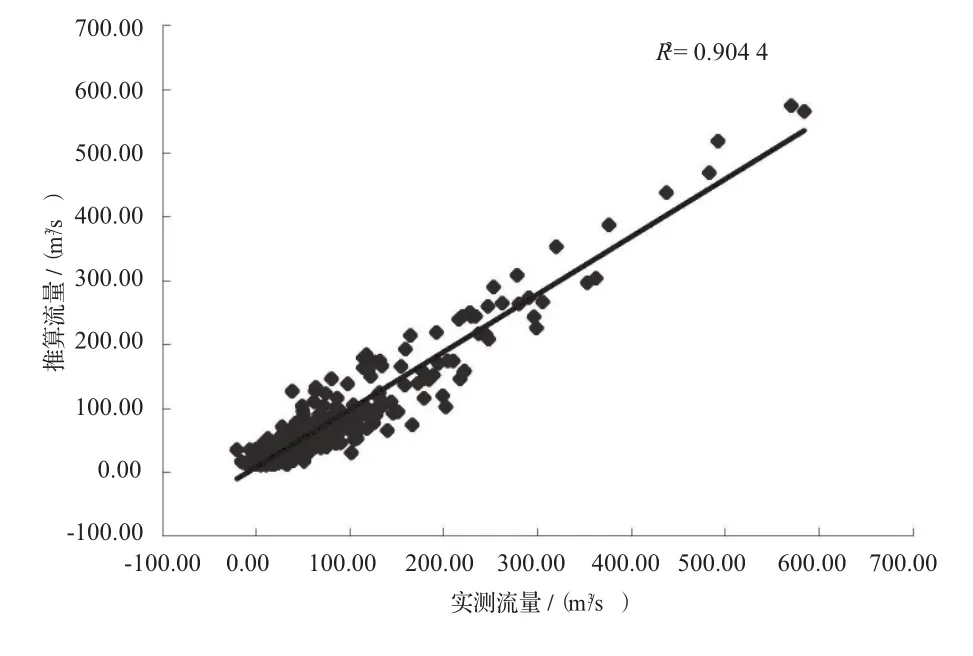
图3 港口水位与港口站流量的回归计算与实测流量关系图
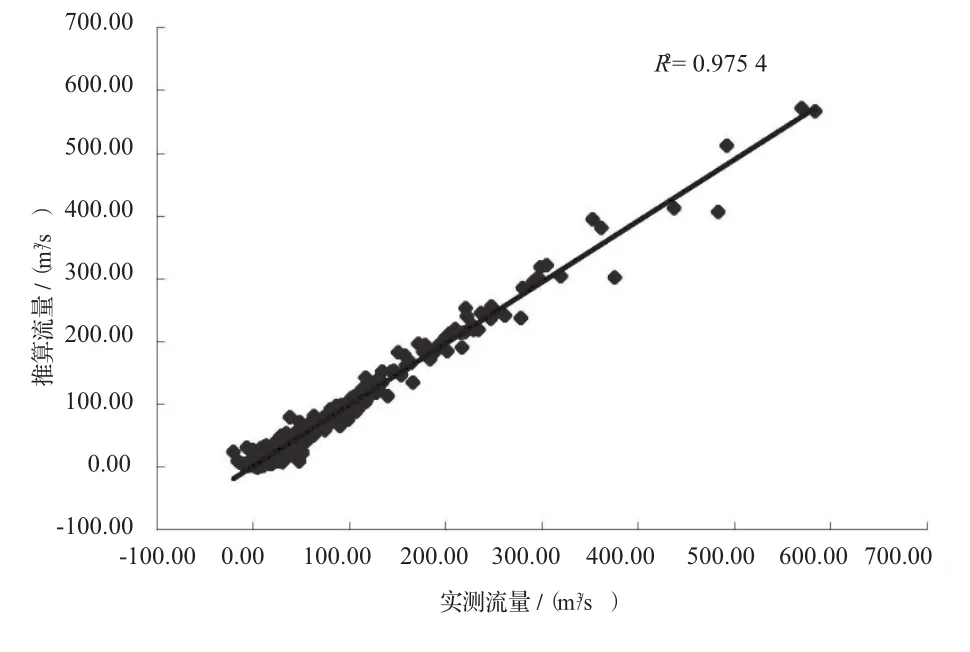
图4 港口、梅溪水位与港口站流量回归计算与实测流量关系图
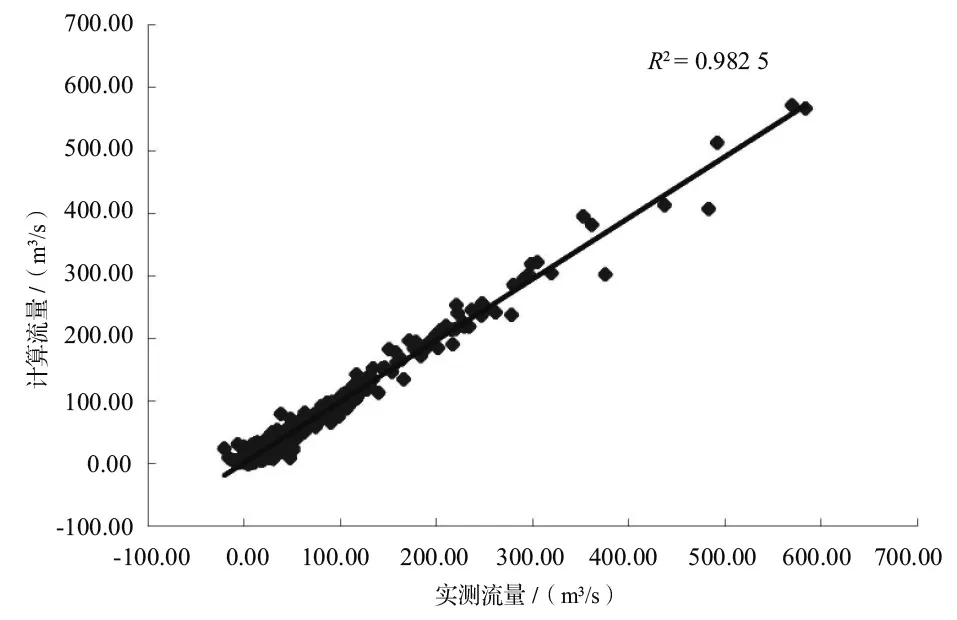
图5 港口、梅溪、杨家埠水位与港口流量回归计算与实测流量关系图

图6 港口、横塘村、梅溪、杨家埠水位与站港口站流量回归计算与实测流量关系图

图7 港口、横塘村、梅溪、杨家埠、杭长桥水位与港口站流量回归计算与实测流量关系图
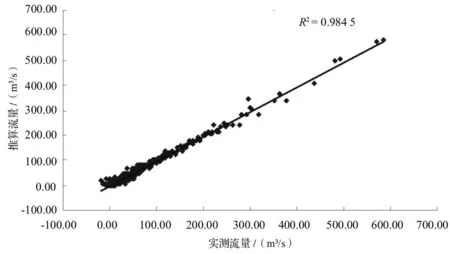
图8 港口、横塘村、梅溪、杨家埠、杭长桥、小梅口水位与港口站流量回归计算与实测流量关系图
5 结论和建议
(1)利用水文站实测水位、流量与上下游辅助水位,按投影寻踪回归分析方法建立水位推流模型推流,可以有效减少流量测次,提高推流精度,实现流量自动监测和预警。
(2)水面比降更能综合反映河道行洪能力的变化,特别是一些受洪水涨落、回水顶托等影响的水文站,都可以在测验断面上下游合适河段设立辅助水位,从而优化、调整已有流量监测策略。
(3)河道行洪能力受人类活动、断面冲淤变化等复杂因素影响,借用上一年的水位、流量关系推求本年河道实时流量,仍存在一定程度的不确定性。因此,在推流过程中需进行适当次数的实测流量校验,一经发现推流成果与实测流量有明显偏离,应加入当年实测成果,重新修正推流模型。
参考文献:
[1] 浙江省水利厅.浙江省河流手册[M].北京:水利水电出版社,2016.
[2] 伍远康,王红英,陶永格,等.浙江省无资料流域洪水预报方法研究[J].水文,2015,35(6):24 - 29.
[3] 刘慧敏,王宏强,黎湘.基于RPROP算法目标识别的数据归一化研究[J].现代雷达,2009,31(5):55 - 60.
[4] 葛守西.现代洪水预报技术[M].北京:水利水电出版社,1999.
