2015年华南区域模式贵州区域2 m气温预报偏差分析

2018-05-25朱文达刘彦华

中低纬山地气象 2018年2期

朱文达，张媛，杨静,刘彦华

(1.贵州省气象台，贵州贵阳 550002；2.民航贵州空管分局，贵州贵阳 550012)

1 引言

伴随互联网云技术的发展，数值预报云使得区域气象中心的数值预报产品实现共享。在数值预报云的支持下，贵州实现对华南区域模式的图形和数据快速共享。为更好的应用该模式，有必要对其在贵州的预报偏差进行分析，从而了解华南区域模式在贵州的预报能力。贵州具有地势高差悬殊，垂直方向差异大，各地气候差别大，天气变化剧烈，天气系统复杂的特点，这导致气温预报成为贵州区域天气预报的最困难的问题之一。

对于模式气温预报偏差的原因分析和订正方法研究一直被学术界和数值模式应用部门热衷探讨。目前用于评估模式气温预报偏差的统计方法较为成熟，智协飞[1]等对模式气温进行贝叶斯模式平均试验，对模式采用均方根误差、距平相关系数、连续等级概率评分等统计量从年际年代际上进行检验、评估。除多[2]等通过地面观测站资料，运用偏差、标准偏差和相关系数等统计量评估了Modem-Era Retrospective Analysis for Research and Applications(简称：MERRA)在分析资料地面气温产品在青藏高原的适用性,指出MERRA资料在青藏高原地面气温表达方面有一定优势。贾佳[3]等基于观测资料分析了高温热浪发生的时空变化特征，对高温热浪进行了分级，运用滑动t检验、Mann-Kendall(MK)方法分析其变化趋势中的突变特征。张寅[4]等利用美国大气辐射测量项目(ARM)制作的“气候模拟最佳估计”观测数据集，检验National Centers for Environment Prediction(美国环境预报中心，NCEP)Global Forecast System(全球预报系统，GFS)2001—2008年在ARM Southern Great Plains站点预报的大气温度、相对湿度和云量的垂直分布，通过模式预报的气温每6 h时间演变对比，得出NCEP GFS能较好地预报出温度垂直分布的季节变化。影响模拟气温预报的因素众多，何光碧[5]等分析了复杂下垫面和降水对气温预报的影响，得出复杂地形对模式预报的影响较大。姜燕敏[6]等从模式水平分辨率角度评估了模式气温预报的能力，发现模式分辨率的提高，能够更好的模式气温和各热通量，尤其是在东亚地区年平均气温的模拟中表现出一定的优势。武敬峰[7]等对青藏高原东侧复杂地形下的中央台精细化气温预报进行了检验，指出造成气温偏差的主要原因是降水、冷暖平流和天气系统强弱。在模式气温偏差分析和产生原因研究的基础上，出现2种改进模式气温预报偏差的方法。一种是模式改进，万子为[8]等通过改进模式积云对流参数化方案中的浅对流触发函数，改进模式2m气温的预报偏差。另一种是统计订正，以吴启树[9]等提出的准对称混合滑动训练期方法和国家气象中心的MOS(Model Output Statistics)系统[10]为代表，能够对模式产品有较大的提高；同时，赵声蓉[11]评估多模式温度集成预报发现，其能够有效避免系统误差，有着较高的预报精度。此外，针对影响模式性能评估的观测数据的质量控制和模式数据插值到站点的插值方法也有专家和学者进行了研究。张颖超[12]等基于粒子群改进的相空间重构法和极限学习机的集成学习算法，对地面气温观测质量控制方法进行了改进。赵滨[13]等建立了新的近地面要素三维插值方法，确保预报和观测在三维空间上保持一致，以减少因垂直方向的一致性问题导致的2 m气温评估偏差。

针对华南区域模式气温的预报结果，本文对2015年模式预报和实况偏差进行分析，研究其时间演变特征和空间分布规律；同时分析2 m气温预报偏差的空间分布特点。从而客观评价华南区域模式在贵州的气温预报能力，为预报员制作智能网格气温预报主观订正和模式客观释用设计提供依据和支撑。

2 资料和方法

2.1 资料选取

模式资料选取2015年华南区域模式GRAPES (Global/ Regional Assimilation and Prediction System)[14]08 h起报的2 m气温预报结果，时间间隔为6 h。其中，最大预报时效为48 h的样本有155个，集中在1—6月；最大预报时效为24 h的样本有152个，集中在7—12月(表1)。实况资料采用贵州区域84个国家站2 m气温观测资料，台站分布(图1)能够表征贵州复杂下垫面环境和海拔差异。同时在分析中选用了5个指标站，分别为贵阳、威宁、汇川、兴义和铜仁站。实况观测数据和模式数据中存在部分数据的缺测，计算时从样本数中剔除，不参与统计量的计算和主分量的分析。

2.2 方法介绍

模式预报2 m气温的偏差计算，首先采用双线性插值方案[15]将模式结果格点场插值到站点，然后采用模式站点结果减实况的方式得到气温预报偏差。针对偏差场，选用统计量方差、相关系数等，进行时间演变特征分析；同时在季节内进行Principal Component Analysis(主分量分析,简称PCA)[16]，主分量个数的选取采用χ2检验的方法[16-17]。

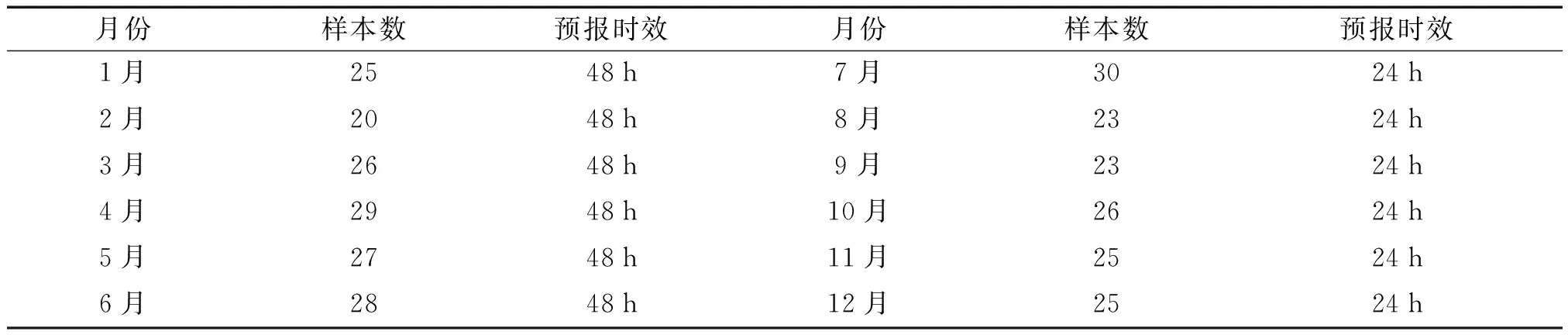
表1 模式数据样本数逐月分布Tab.1 The number of model samples per month

图1 实况站点分布(填色为站点海拔高度，单位：m)Fig 1 The distribution of observation stations(shaded for altitude,unit:m)

设已选取k个主分量，对应的特征值为λ1,λ2,...,λk，余下的特征值为λk+1,...,λp,则统计量

χ2=-F0[ln(λk+1...λp)-(p-k)ln(θ)]

是遵从自由度为(p-k+2)(p-k+1)/2的χ2分布。其中

3 偏差时间特征分析

3.1 时间平均特征

运用2015年全年的模式预报结果减去相对应的实况观测值，得到全年307个起报场84个观测站48 h(24 h)预报时效内逐6 h的偏差。对偏差场做时间平均，得到全年84站48 h(24 h)预报时效内逐6 h的平均偏差情况(图2a)，对偏差场求绝对值后做时间平均，得到平均绝对误差(图2b)。

图2 84个国家站2 m气温偏差全年时间平均特征,(a)全年时间平均偏差，(b)全年时间平均绝对误差(x坐标为模式预报时间，y坐标为偏差或绝对误差，单位：℃)Fig.2 The annual mean temperature bias of 84 observation stations,a:The annual mean temperature bias,b:The annual mean temperature absolute bias(X-axis:model forecast time,Y-axis:temperature bias/,temperature absolute bias unit:℃)

84个站的全年平均的偏差各预报时次间存在明显差异，尤其是06 h、12 h、30 h和36 h的负偏差更为明显。总体平均偏差水平在-3～4 ℃之间，最大正平均偏差出现在06 h，最大的负平均偏差出现在30 h。大部分站点的平均偏差以24 h为周期变化。年平均的绝对误差反映的06 h和30 h平均绝对误差最大的信号更为显著，平均绝对误差的大小同样呈现以24 h为周期变化。总体平均绝对误差的大小能控制在4 ℃以内。无论是年平均偏差还是年平均绝对误差，在00时都有0～2 ℃左右，这表明模式的初始场与观测实况仍存在偏差。

模式结果与实况相减得到的偏差按季节进行时间平均处理，其中冬季为12—次年2月，春季为3—5月，夏季为6—8月，秋季为9—11月。得到基于84个站的季节平均的偏差(图3a、3c、3e、3g)，同时计算得到了季节平均的绝对误差(图3b、3d、3f、3h)。季节平均的偏差表明模式偏差在冬季(图3a)大部分站点为正偏差，而夏季(图3e)大部分站点为负偏差，春季(图3c)和秋季(图3g)为过渡阶段。大部分站点最大季节平均偏差同样出现在30 h和36 h的预报时效(秋季除外)，次大的季节平均偏差出现在06 h和12 h，这与年平均的结果一致。各季节的平均绝对误差，在冬季(图3b)和夏季(图3f)大部分站点的绝对误差在3 ℃左右，个别站点接近4 ℃，对应的在春季(图3d) 和秋季(图3h)大部分站点的绝对误差在3 ℃以内。

图3 84个国家站2 m气温偏差季节平均特征,a(c、e、g)、冬季(春季、夏季、秋季)平均偏差,b(d、f、h)、冬季(春季、夏季、秋季)平均绝对误差(x坐标为模式预报时间，y坐标为偏差或绝对误差，单位：℃)Fig.3 The seasonal average temperature bias of 84 observation stations,a ( c,e,g):The seasonal average temperature bias in Winter(Spring,Summer,Autumn),b ( d,f,h):The seasonal average temperature absolute bias in Winter (Spring,Summer,Autumn)(X-axis:model forecast time,Y-axis:temperature bias/temperature absolute bias unit:℃)

无论是年平均还是季节平均，2 m气温偏差都在06 h、12 h、30 h和36 h(即午后到傍晚时段)更为显著，以24 h为周期演变，最大平均绝对误差在4 ℃左右。同时季节平均还反映出冬季偏高、夏季偏低；春秋季节相对较为平稳的，且为冬季与夏季两种位相的过渡期。针对于此，对于模式订正设计，在模式在预报时效上，订正权重以24 h为周期变化，且06 h、12 h、30 h和36 h订正权重相对更大；在季节变化上，冬季减小，夏季增加，春秋季节周期变化为主。

3.2 指标站时间特征分析

选取了贵阳、威宁、铜仁、兴义和汇川5个指标站,给出对应的逐月的模式2 m气温偏差演变情况(图4)，图4中x坐标为模式起报时间，填色序列为模式预报时效内各个预报时次的气温偏差分布情况。受篇幅限制，选取各个季节的中间月为代表。季节中间月的选取能有效减少季节变化信号对偏差分析的影响。

5个站1月(图4 a1、b1、c1、d1、e1)气温偏差反映的情况与年平均和季节平均的结论一致，在1月，模式预报气温存在明显偏高，个别时次偏高超过10 ℃。4月(图4 a2、b2、c2、d2、e2)气温偏差出现明显波动，负偏差开始增多；受副热带系统影响的兴义站(图4 d2)出现较多时次的偏低，其它4站偏高和偏低的时次基本相当。进入贵州易发高温天气的7月(图4 a3、b3、c3、d3、e3)，除威宁站(图4 b3)和汇川站(图4 e3)外，其余3站大部分预报时段都表现出明显的偏低，尤其是常年气温较高的铜仁站(图4 c3)在7月中下旬模式预报出现长时间的偏低。进入秋季的10月(图4 a4、b4、c4、d4、e4)，偏差开始向偏高位相转换，5站中除兴义站(图4 d4)外大部分时段都出现了明显的偏高，兴义站的偏差由偏低向偏高转换发生在11月中旬(图略)，落后于其它站点2周左右，这与兴义站所在的纬度存在较大关系。

图4 5个指标站2 m气温偏差时间演变特征,a、贵阳站，b、威宁站，c、铜仁站，d、兴义站，e、汇川站,a1、1月，a2、4月，a3、7月，a4、10月(b、c、d、e同a，只是站点有差别)(x坐标为模式时间，y坐标为偏差，单位：℃)Fig.4 The temperature bias of 5 observation stations,a:Guiyang,b:Weining,c:Tongren,d:Xingyi,e:Huichuan,a1:Jan,a2:Apr,a3:July,a4:Oct (b,c,d,e same as a except for stations),(X-axis:model forecast time,Y-axis:temperature bias,unit:℃)

指标站的偏差数值大小与年平均和季节平均结果存在差异，指标站偏差最小值的时间出现在夏季，偏差波动幅度较为平缓。反而在年平均和季节平均中偏差小的冬季和转换季节中的春季、秋季在指标站中有着较大的偏差振幅。指标站的偏差时间演变规律和全部站点的年平均和季节平均结果在冬季偏高、夏季偏低的结论上保持一致，但偏差大小上存在一定差异，指标站的偏差明显大于全部站点的年平均和季节平均；指标站的最大偏差出现在偏差位相转化的春季和秋季中，反而在夏季最为平缓。不同站点间气温偏差时间演变存在明显差异，海拔、纬度、天气系统都会影响模式的气温预报，从而影响偏差时间演变规律。在模式气温订正中，需要考虑海拔差异、纬度高低、季节变化、大气环流转换、天气尺度系统等因素的影响。

4 多统计量集成图分析

Karl E.Taylor[18-20]等针对多统计量的集成问题，设计了Taylor(泰勒)分析。图中经过标准化的参考场，其自相关、标准差为1，均方根误差(Root-Mean-Square Error，简写RMSE)为0。RMSE表示对比场和参考场的相似性；相对参考场的标准差表征对比场与参考场中心振幅的对比情况[21-22]。

此处选用年平均2 m气温偏差场作为参考场，月平均2 m气温偏差场作为对比场，对各场求距平标准化后，进行Taylor(图 5)分析。图中填色点代表了1—12月的月平均场相对于年平均场的对比情况，标记1～9代表模式预报的00～48 h时效，参考点REF为年平均结果；月平均到原点距离表示气温偏差月平均相对于参考点的标准差；月平均的方位角余弦表示其与参考点的相关系数；月平均结果到参考点的距离代表其均方根误差。其中7—12月的30～48 h预报时效作为缺测数据，不计入计算。

月平均的2 m气温偏差相对于年平均，大部分月份和预报时效有较好的相关性，在0.6以上，仅有个别月的预报时效相关在0.5以下。同样，从标准差可以反映出，28.6%落在距离1外，3.6%落在均方根比为1.75的距离外；月平均偏差标准差有71.4%小于全年平局，尤其是夏季的JJA(6—8月)的标准差在0.75内，6—7月的标准差基本落在0.5以内，这与年平均和季节平均及指标站的结论一致。3.6%标准差位于1.75距离外的主要集中在季节转换和强对流频发的春季；28.6%位于1距离外多集中出现在冬春季节。同时RMSE大多分布在0.3～0.75的范围内。在天气环流形势稳定、无明显冷空气活动的夏季，月平均的偏差波动幅度较小；对于受频繁活动冷空气影响的冬季和环流转换的春季，月平均的偏差波动幅度较大。

图5 多统计量集成图(泰勒图)Fig.5 The Taylor diagram

5 PCA特征

对偏差场求距平标准化后，利用PCA算法[16]，得到季节内特征向量和对应的时间函数。考虑去除季节变化因素影响，采用季节内经验正交函数分解，同时基于样本预报时效的统一性，仅对0～24 h预报时效进行经验正交函数分解。根据所得PCA结果，基于χ2大于0.05显著水平标准[16-17]，前9个主分量达到截留标准。受篇幅限制，同时基于前文春季处于转换季节和夏季较为平稳的结论，此处仅对12 h预报场的春季和夏季第1和第2特征向量进行分析(图6)。春季12 h预报场的第1和第2特征向量对应的特征值累计方差贡献率[23-24]为73.9%，其中第1特征向量的特征值占66.7%；对应的夏季的为49.4%和40.7%。

对于第1特征向量，春季(图6 a)和夏季(图6 e)都表现出同位相特征，春季都为负，夏季都为正，所有站点随时间函数保持同性变化。第2特征向量(图6 b、6 f)则出现显著的位相差异，基本以贵州中部为分界线，以南以西为正位相，其余则为负位相。

春季的第1特征向量对应的时间函数(图6 c)在3—4月波动幅度较大，呈10～20 d周期振荡，进入5月后逐渐平缓；结合第1特征向量的位相特征，可以得出在3—4月全省的气温偏差数值和波动幅度较大。春季的第2特征向量对应的时间函数(图6 d)呈10～20 d振荡，波动幅度较小；结合第2特征向量的位相特征，以贵州中部为界，南、北气温偏差呈现10～20 d反位相振荡特征。

图6 PCA 12 h预报时效的特征向量和时间函数,a春季第1特征向量，b春季第2特征向量,e、f同a、b但季节为夏季,c春季第1特征向量对应的时间函数，d春季第2特征向量对应的时间函数，g、h同c、d但季节为夏季(a、b、e、f的x坐标为经度，y坐标为纬度，单位：°c、d、g、h的x坐标为时间变量，单位：d，y坐标为特征向量对应的时间函数)Fig.6 Eigenvectors and time series of principal component analysis at forecast time 12h,a:The first eigenvector in Spring,b:The second eigenvector in Spring,e,f same as a,b but in Summer,c:Time series of the first eigenvector in Spring,d:Time series of the second eigenvector in Spring,g,h same as c,d but in Summer,(a,b,c,d X-axis:longitude,Y-axis:latitude,unit:°c,d,g,h X-axis:time series,unit:day,Y-axis:The time function of eigenvector)

夏季的第1特征向量对应的时间函数(图6 g)在6—8月整体振幅相对较小，6、8月波动幅度相对7月较为明显，表明在夏季气温偏差较小；7月的时间函数以负值为主，结合夏季第1特征向量位相特征，得出7月的气温偏差以偏低为主，这与指标站和Taylor diagram 得出的结论一致。第2特征向量对应的时间函数(图6 h)大部为负值，8月逐渐转为正值，结合第2特征向量位相特征，贵州中南部在6、7月以偏低为主，北部以偏高为主，进入8月后偏差的符号开始南北对调。

第1特征向量反映的是偏差空间分布的平均状况，从冬季(图略)到秋季(图略)第1特征向量都为同一位相，全部站点气温偏差表现为相同的变化趋势和同位相的空间分布特征，这表明模式预报偏差同位相变化占主导，即全部偏高或偏低的趋势占主导。从第2特征向量开始出现位相的分化，刻画偏差变化趋势和空间分布特征更突出细节；春季贵州西部地区静止锋影响和强对流展对气温偏差的影响、夏季贵州南部地区副热带高压和强降水[25]影响等都在第2～5特征向量(图略)中体现。第1、2特征向量对应的时间函数存在低频振荡特征，周期为10～20 d，这与东亚地区低频冷空气的活动周期和东亚季风的振荡周期一致[26]，可以得出冷空气的低频振荡和东亚季风的低频活动是导致气温偏差周期变化的重要原因之一。

6 结论与讨论

通过对华南区域模式GRAPES 08h预报场的2m气温进行双线性插值到84个国家站后的到的结果与实况观测相减得到偏差，对偏差进行年平均、季节平均、指标站时间演变特征分析、Taylor diagram分析和PCA，得出以下结论：

①年平均和季节平均得出气温偏差在不同模式预报时次存在差异，以06 h、12 h、30 h和36 h(即午后到傍晚时段)最为显著，并且以24 h为周期演变；最大平均绝对误差在4 ℃左右。同时季节平均还反映出冬季偏高、夏季偏低；春秋季节相对较为平稳，且为冬季与夏季两种位相的过度期。

针对于此，对于模式订正设计，在模式在预报时效上，订正权重以24 h为周期变化，且06 h、12 h、30 h和36 h订正权重相对更大；在季节变化上，冬季减小，夏季增加，春秋季节周期变化为主。

②指标站的偏差时间演变规律与年平均和季节平均的结论基本一致，但偏差值明显大于年平均和季节平均；指标站的最大偏差出现在偏差位相转化的春季和秋季中，夏季最为平缓。不同站点间气温偏差时间演变存在明显差异，海拔、纬度、天气系统都会影响模式的气温预报，从而影响偏差时间演变规律。在模式气温订正中，需要考虑海拔差异、纬度高低、季节变化、大气环流转换、天气尺度系统等因素的影响。模式气温偏差的出现不是单一条件导致的，模式后处理订正需要统筹考虑诸因素。

③Taylor diagram 反映出季节间的气温偏差在天气环流形势稳定、无明显冷空气活动的夏季，月平均的偏差波动幅度较小；对于受频繁活动冷空气影响的冬季和环流转换的春季，月平均的偏差波动幅度较大。环流转换、季节变化、冷空气活动可能是导致此特征的重要原因；同时同一起报时次的不同预报时次间的气温偏差也存在明显差异。

④PCA得出方差比占绝对的第1特征向量反映的是偏差空间分布的平均状况，第1特征向量都为同一位相，全部站点气温偏差表现为相同的变化趋势和同位相的空间分布特征，这表明模式预报偏差同位相变化占主导，即全部偏高或偏低的趋势占主导。从第2特征向量开始出现位相的分化，刻画偏差变化趋势和空间分布特征更突出细节，不同季节的天气系统和环流特征的影响表现也更为明显。第1、2特征向量对应的时间函数存在低频振荡特征，周期为10～20 d，与东亚地区低频冷空气的活动周期和东亚季风的低频振荡周一致，冷空气的低频振荡和东亚季风的低频活动可能是导致气温偏差周期变化的重要原因之一。

本文分析了华南区域模式2 m气温的时间演变规律和空间分布特征，运用多种统计方法对偏差进行了分析，得出偏差不同预报时效之间的周期变化规律，不同季节的偏差振幅差异，空间站点分布的特征；偏差对于天气系统活动的响应，偏差与冷空气及东亚季风低频振荡的关系。以上结论是下一步模式客观释用订正工作方案设计的基础，方案要遵循预报时效内的周期变化规律，订正权重需有季节变化，影响因子包含空间分布和海拔差异。同时方案还需考虑冷空气和东亚季风活动的低频振荡特征，不同系统的影响率要依据PCA特征值方差贡献率分布，主要影响系统的选取依据χ2检验结果。此外，在面对环流转换、季节变化、转折天气时，预报员的主观订正尤为重要，需参考偏差Taylor diagram反映的振幅变化特征，选取适当订正量度。对于导致偏差产生的数值模式动力框架、参数化方案等模式本身的问题仍需要后期开展大量工作研究。

参考文献

[1] 智协飞,王晶,林春泽,等.CMIP5多模式资料中气温的BMA预测方法研究[J].气象科学,2015,35(4)：405-412.

[2] 除多,杨勇,罗布坚参,等.MERRA再分析地面气温产品在青藏高原的适用性分析[J].高原气象,2016,35(2)：337- 350.

[3] 贾佳,胡泽勇.中国不同等级高温热浪的时空分布特征及趋势[J].地球科学进展,2017,32( 5) :546- 559.

[4] 张寅,罗亚丽,管兆勇.NCEP 全球预报系统在ARM SGP站点预报大气温度、湿度和云量的检验[J].大气科学,2012,36(1):170- 184.

[5] 何光碧,肖玉华,张利红,等.GRAPES-Mesov3.1在西南地区2011年汛期的预报检验分析[J].成都信息工程学院学报,2015,30(1):63 -71.

[6] 姜燕敏,黄安宁,吴昊旻.不同水平分辨率BCC_CSM模式对中亚地面气温模拟能力评估[J].大气科学,2015,39 (3):535-547.

[7] 武敬峰,黄超,陈茂强.川西高原地区SCMOC温度精细化指导预报质量检验及影响因子分析[J].高原山地气象研究，2017,37(1):41- 48.

[8] 万子为,王建捷,黄丽萍,等.GRAPES-MESO模式浅对流参数化的改进与试验[J].气象学报,2015,73( 6):1 066-1 079.

[9] 吴启树,韩美,郭弘,等.MOS温度预报中最优训练期方案[J].应用气象学报,2016,27(4):426-434.

[10]刘还珠,赵声蓉,陆志善,等.国家气象中心气象要素的客观预报—MOS系统[J].应用气象学报,2004,15(2):181-191.

[11]赵声蓉.多模式温度集成预报[J].应用气象学报,2006,17(1):52- 58.