Perturbation Theory of Fractional Lagrangian System and Fractional Birkhoffian System

，

1．School of Mathematics and Physics，Suzhou University of Science and Technology，Suzhou 215009，P．R．China；

2．College of Science，Nanjing University of Science and Technology，Nanjing 210094，P．R．China；

3．College of Civil Engineering，Suzhou University of Science and Technology，Suzhou 215011，P．R．China

［STHZ］0 Introduction［ST］

In 1917，adiabatic invariant was first proposed by Burgers［1］．A certain physical quantity is called adiabatic invariant of a system if it varies more slowly than the parameters which change very slowly．In fact，the parameter changing very slowly can be expressed as the action of small disturbance．Under the action of small disturbance，the original symmetry and conserved quantity may change．At the same time，because perturbation to symmetry and adiabatic invariant concern the integrability of the equations of motion of mechanical systems，they were studied by many scientists，and many important results were obtained［2－9］．However，almost all of those results about adiabatic invariant referred to only integer order derivatives of the variables．Therefore，there is still much to do on the aspect of the noninteger order derivatives of the variables．Hence，in this paper，we intend to study perturbation to symmetry and adiabatic invariant in terms of fractional calculus．

Fractional calculus has been studied for more than 300years by many famous mathematicians，and many significant results about fractional calculus have been obtained［10－17］．Besides，based on the fractional calculus，Riewe［18－19］investigated the version of the Euler－Lagrange equations for the problem of the calculus of variations with fractional derivatives under the conservative and non－conservative cases respectively．Since then，many further studies on fractional problems can be found［20－38］．For example，in 2002，Agrawal［20］proved a formulation for the variational problem in the sense of Riemann－Liouville derivatives．Then Baleanu and Avkar［26］used those Euler－Lagrange equations to study the problem with Lagrangian which is linear on the velocities．Frederico and Torres［27］used the notion of the Euler－Lagrange fractional extremal［20］to prove a Noethertype theorem．Using the similar method adopted in Ref．［27］，Zhou［39］studied the fractional Pfaff－Birkhoff principle in terms of Riemann－Liouville derivatives，and obtained the fractional Birkhoff equations，the corresponding transversality conditions and the fractional－conserved quantities．Based on the results of Refs．［27，39］，we intend to study the adiabatic invariant of the fractional calculus of variations．

1 Preliminaries

In this section，some relevant knowledge would be recalled．

Definition 1［14］Letfbe a continuous and integrable function in the interval［t1，t2］，for allt∈［t1，t2］，the left Riemann－Liouville fractional derivativet1Dαtf（t）of orderα，and the right Rie－mann－Liouville fractional derivative（t）of orderβ，are defined as follows

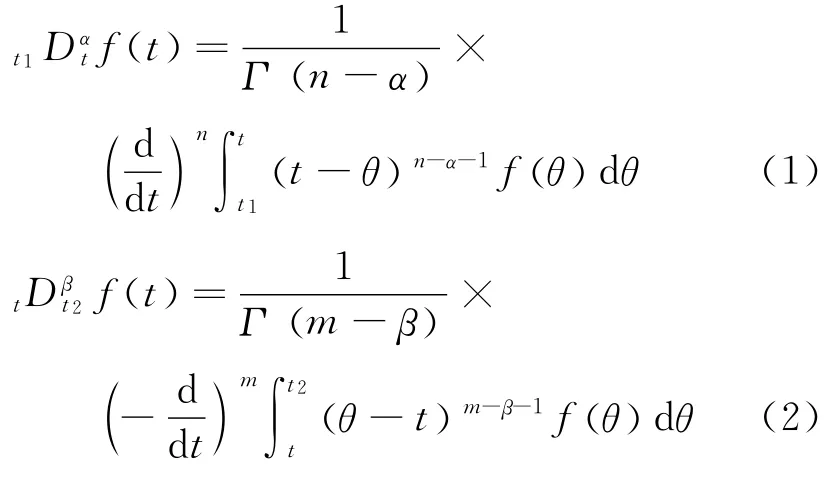
whereΓ（·）is the Euler Gamma function，α，βare the orders of the derivatives satisfyingn－1≤α＜n，m－ 1 ≤β＜m，m，n∈［WTHZ］N［WTBX］．Ifα，βare integers，those derivatives are defined in the usual sense，that is

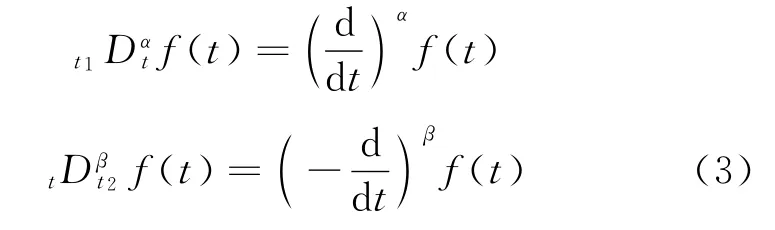
In this paper，we assume that 0＜α＜1，0＜β＜1．

In Ref．［20］，Agrawal considered the functional

whereq（a）＝qa，q（b）＝qband the LagrangianL：［WTHZ］R［WTBX］is aC2function with respect to all its arguments．And he got the following fractional Euler－Lagrange equation in terms of Riemann－Liouville derivatives

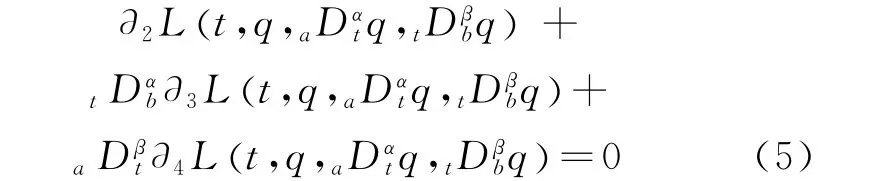
In Ref．［39］，Zhou and Zhang studied the extremum for the following functional

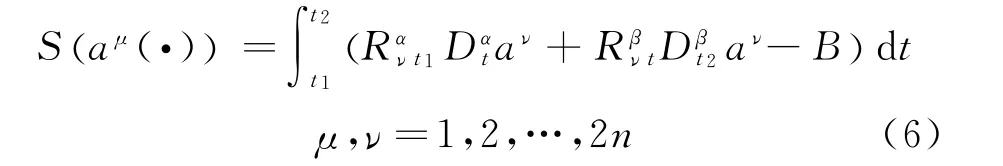
whereare the Birk－hoff′s functions，B＝B（t，aμ）is the Birkhoffian，and they are bothC2functions with respect to all their arguments．And they obtained the following fractional Birkhoff equations

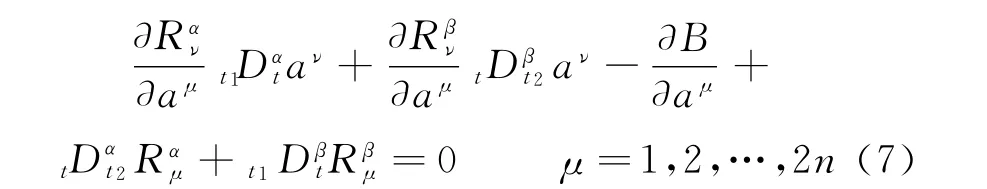
Definition 2［27］Given two functionsf，g∈C1［a，b］，we introduce the following notation

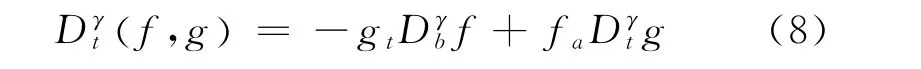
wheret∈ ［a，b］，and．

The linearity of the operatorsaandtimplies the linearity of the operator

Ifγ＝1，the operatorreduces to

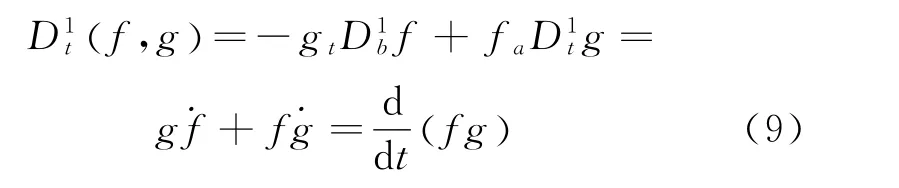
2 Fractional Adiabatic Invariants

In this section，we study adiabatic invariants under the general and special infinitesimal transformations for the fractional Lagrangian system and the fractional Birkhoffian system．

2．1 Adiabatic invariants for the fractional Lagrangian system

Firstly，let′s consider only the infinitesimal transformation forq

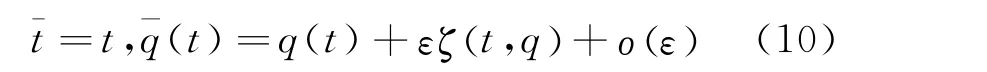
whereζis called the infinitesimal generator．

Theorem 1［27］Under the infinitesimal transformation（10），if the condition

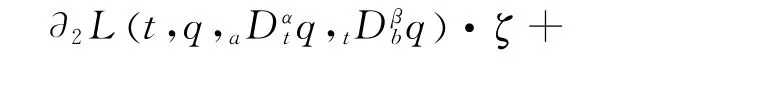
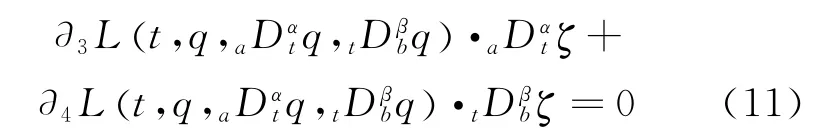
holds，then

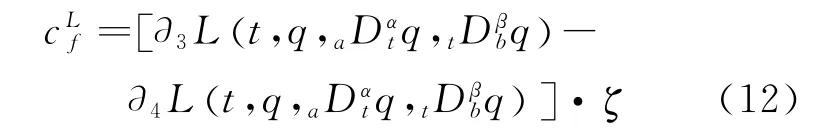
is a fractional－conserved quantity．

Theorem 2［27］Under the infinitesimal transformations

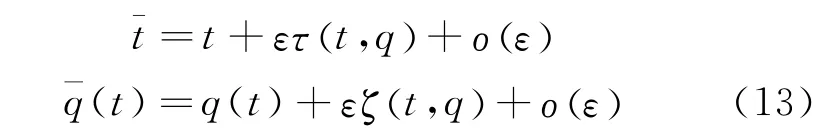
if functional（4）is invariant，i．e．

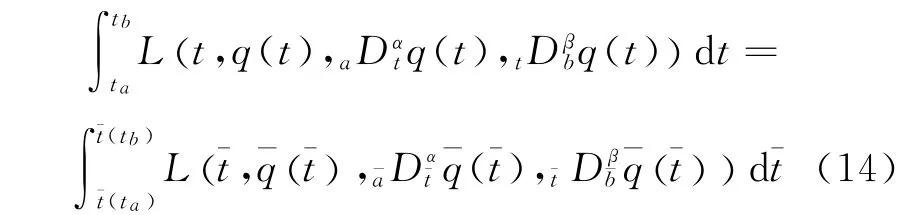
for any subinterval ［ta，tb］ ［a，b］

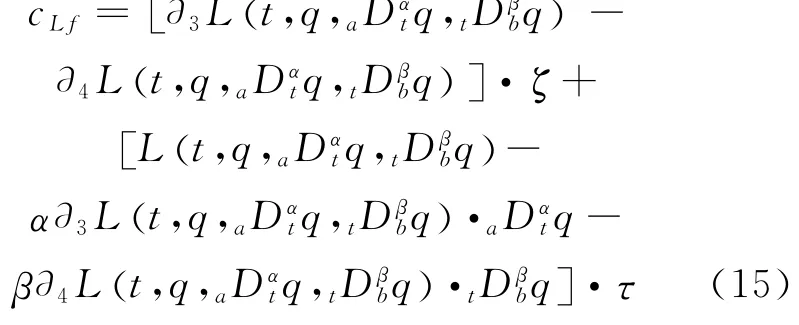
is a fractional－conserved quantity．

Definition 3 If

is in direct proportion toεz＋1

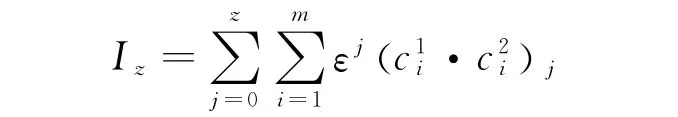
is called az－th order adiabatic invariant of a fractional order dynamical system．

For the fractional Lagrangian system （Eq．（5）），ifζ0satisfies Eq．（11），the following exact invariant exists

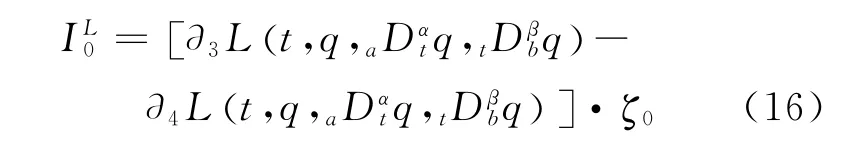
Similarly，ifτ0，ζ0satisfy Eq．（14），the exact invariant exists as follows

Suppose the fractional Lagrangian system（Eq．（5））is disturbed by small quantityεQ，then we can get the disturbed fractional Euler－La－grange equation

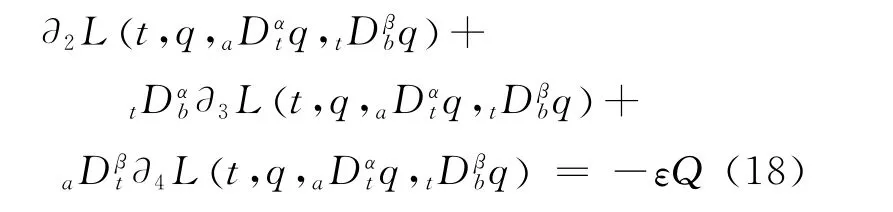
Under the action of small force of perturbationεQ，the invariant of the system may vary．Suppose that the disturbed infinitesimal generatorζcan be expressed as

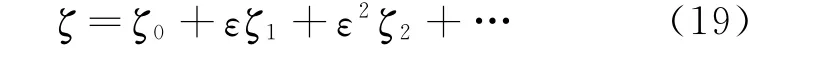
we have Theorem 3as follow．

Theorem 3 For the disturbed fractional Lagrangian system （Eq．（18）），if the infinitesimal generatorsζjj＝0，1，2，…（

）satisfy

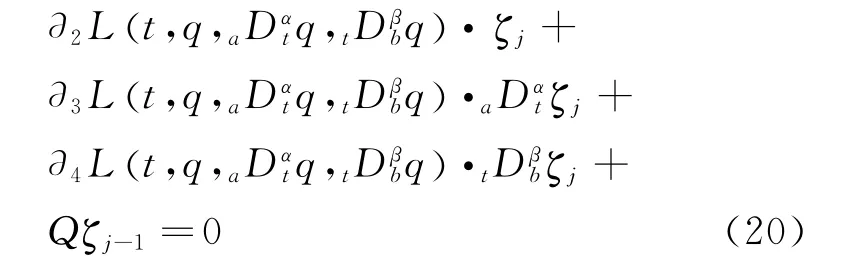
the disturbed fractional Lagrangian system has az－th order adiabatic invariant

where we setζj－1＝0，whenj＝0．

Proof From the disturbed fractional Euler－Lagrange equation and the condition，we have

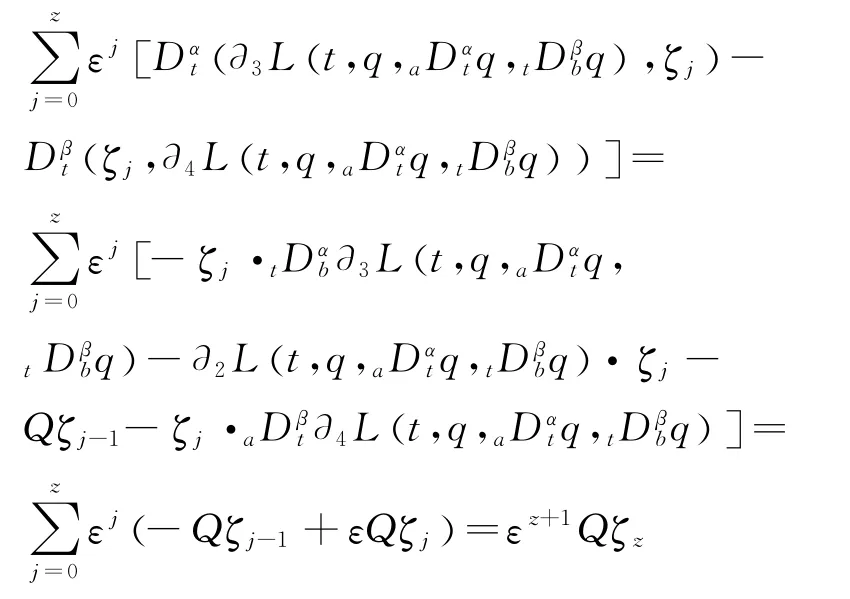
Hence，the proof is completed．

Theorem 4 Under the infinitesimal transformations

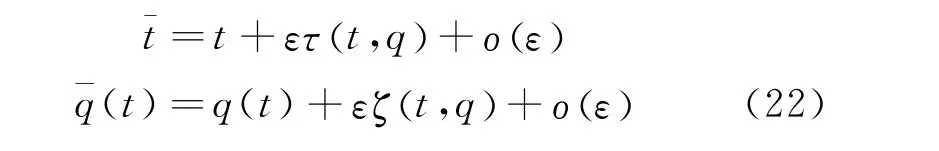
where

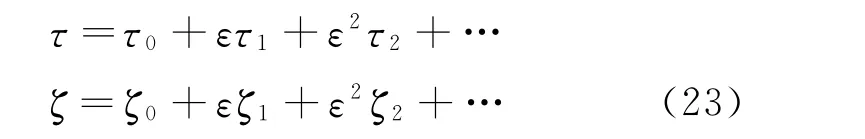
the disturbed fractional Lagrangian system （Eq．（18））has az－th order adiabatic invariant

Proof In order to considertas a dependent variable，we use a Lipschitzian one－to－one transformation

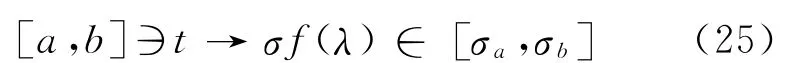
which satisfiest′σ＝f（λ）＝1whenλ＝0，t（σa）＝a，t（σb）＝b．

From the definitions of the right Riemann－Liouville fractional derivative and the left Riemann－Liouville fractional derivative，we have

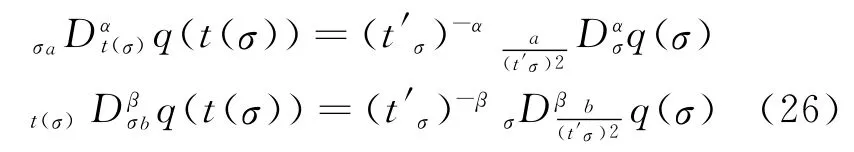
Hence

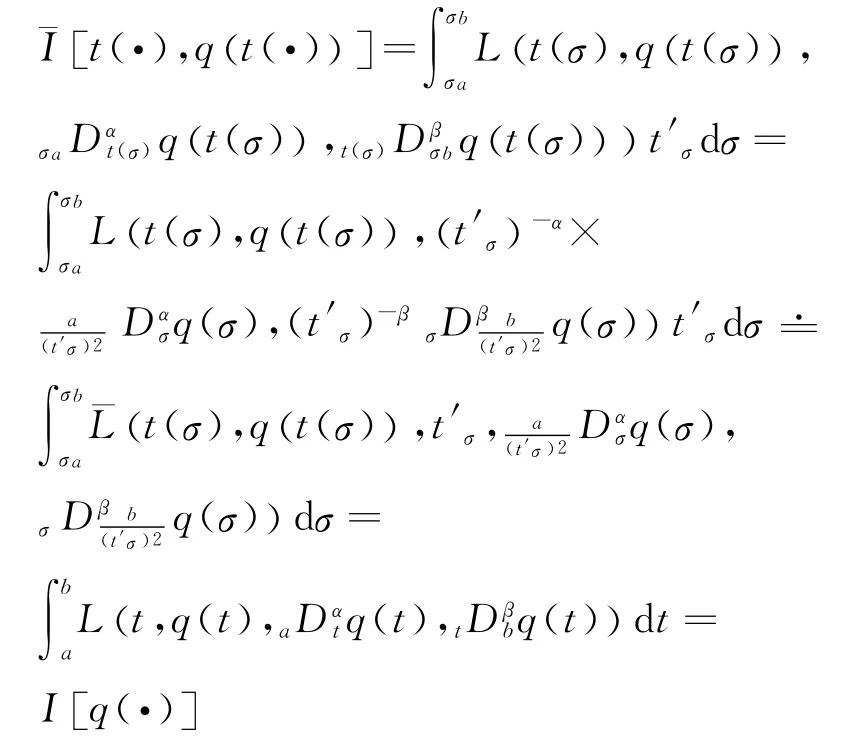
From Theorem 3，we can obtain

Ifλ＝0，we can get

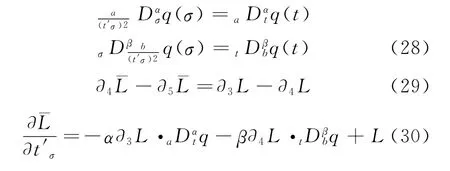
Therefore，whenλ＝0，we have

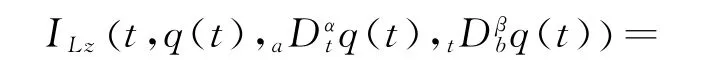
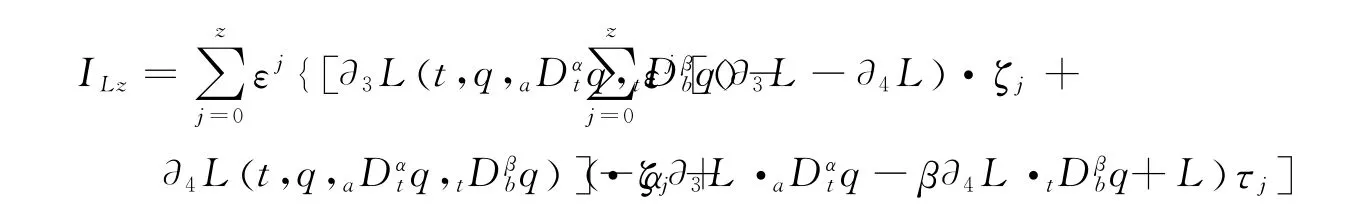
The proof is completed．

2．2 Adiabatic invariants for the fractional Birkhoffian system

We consider only the infinitesimal transformations foraμ

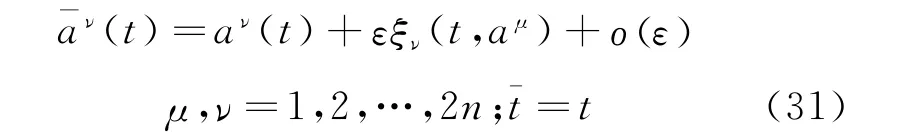
whereξνν＝1，2，…，2n（）are called the infinitesimal generators．

Theorem 5［39］Under the infinitesimal transformations（Eq．（31）），if

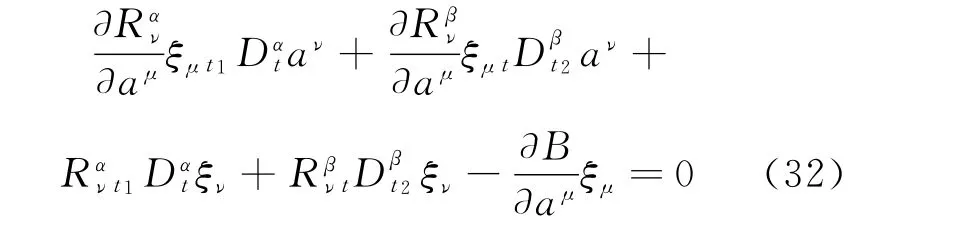
we have

is a fractional－conserved quantity．

Therefore，for the fractional Birkhoffian system（Eq．（7）），ifsatisfies Eq．（32），exact invariant exists as follows

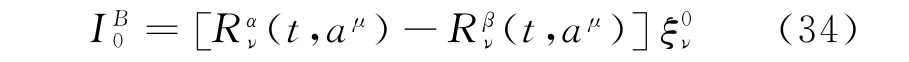
Theorem 6［39］Under the infinitesimal transformations

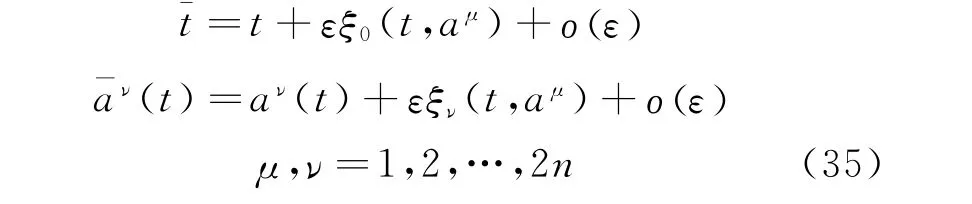
if functional（6）is invariant，i．e．

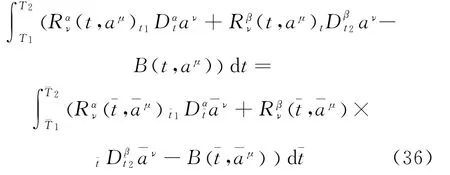
for any［T1，T2］［t1，t2］

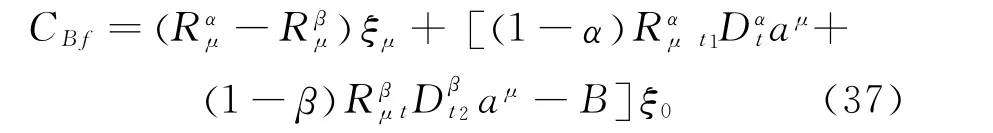
is a fractional conserved quantity for the fractional Birkhoffian system （Eq．（7））．

Therefore，for the fractional Birkhoffian system（Eq．（7）），ifsatisfy Eq．（36），there ex－ists exact invariant

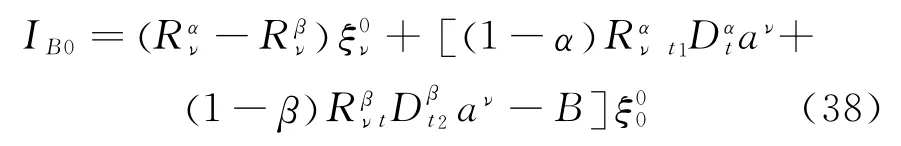
Suppose the fractional Birkhoffian system（Eq．（7））is disturbed by small quantitiesεQμ（μ＝1，2，…，2n），then we can get the disturbed fractional Birkhoff equations

Under the action of small forces of perturbationεQμ，the invariant of the system may vary．Suppose that the disturbed infinitesimal genera－torscan be expressed as

Then we have Theorem 7as follow．

Theorem 7 For the disturbed fractional Birkhoffian system （Eq．（39）），if the infinitesimal generatorsξjμj＝0，1，2，…（

）satisfy

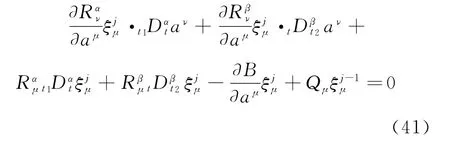
the disturbed fractional Birkhoff system has azth order adiabatic invariant

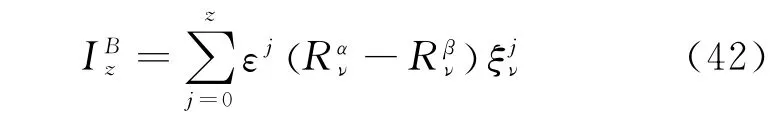
where we set

Proof From the disturbed fractional Birkhoff equations and the condition，we have

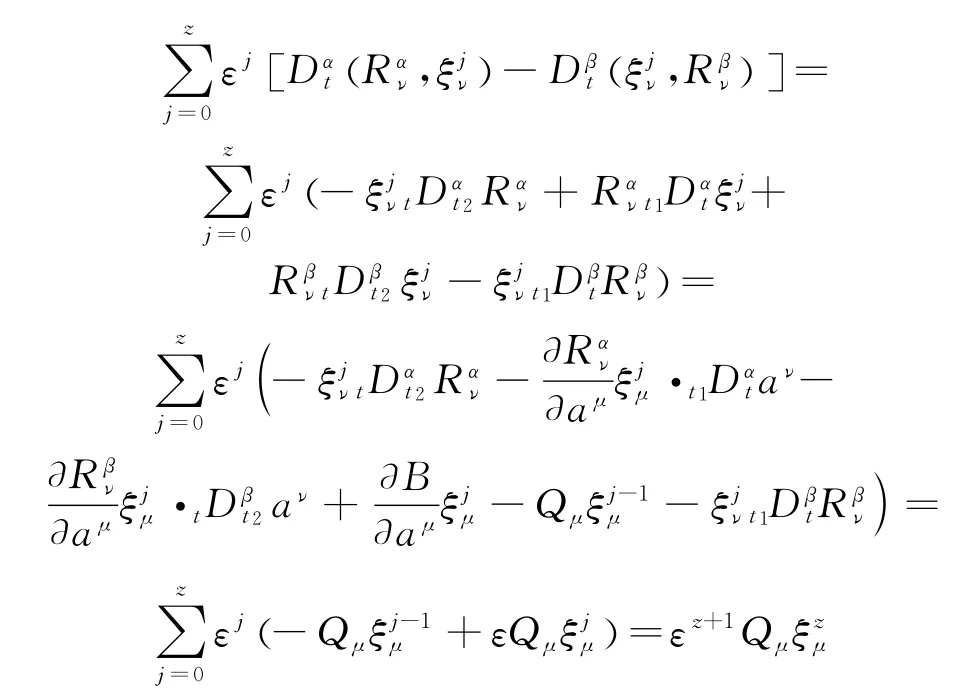
The proof is completed．

Theorem 8 Under the infinitesimal transformations

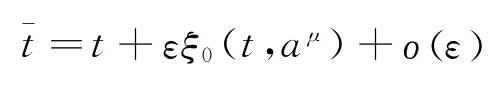
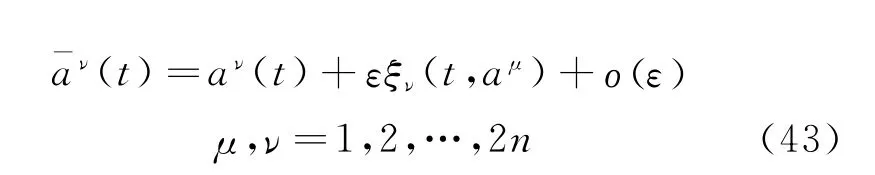
where

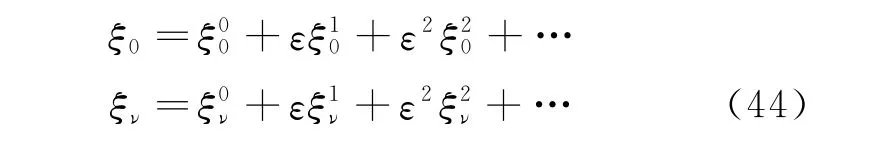
the disturbed fractional Birkhoffian system （Eq．（39））has az－th order adiabatic invariant

Proof Consider a one to one transformation

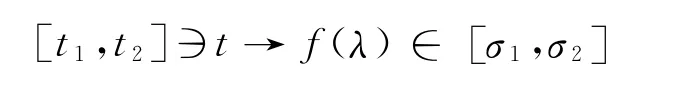
which satisfiest（σ1）＝t1，t（σ2）＝t2andt′σ＝dt（σ）／dσ＝f（λ）＝1，whenλ＝0．

From the definitions of the right Riemann－Liouville fractional derivative and the left Riemann－Liouville fractional derivative，we can get

Forλ＝0，we have

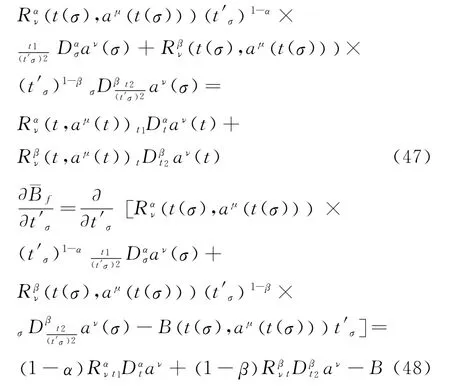
Hence，using the similar method adopted for Theorem 4，from Theorem 7，forλ＝0，we can get

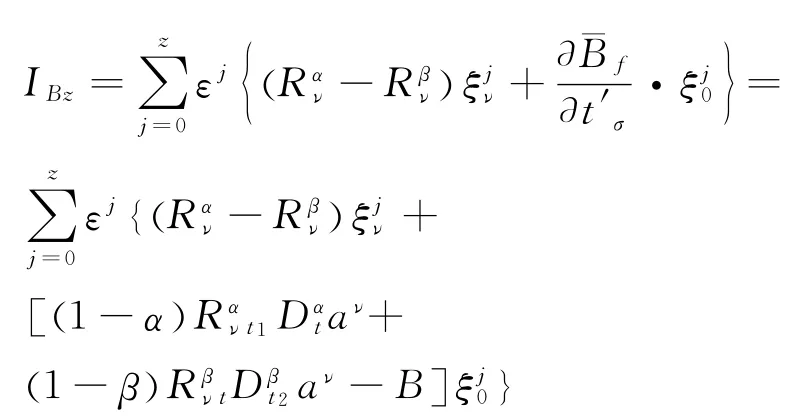
The proof is completed．

3 Two Illustrative Examples

In this section，we give two examples to illustrate the results obtained above．

Example 1 Let us consider the following fractional Lagrangian system

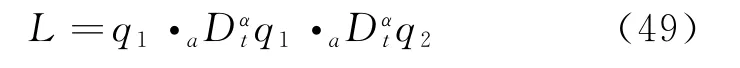
We can verify that

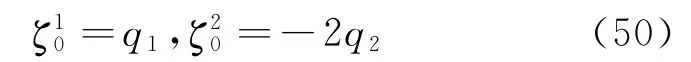
satisfy the condition （11）．Then we can obtain from Eq．（16）that

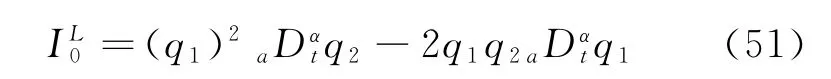
Suppose the system （Eq．（5））is disturbed by the following small quantities

By calculating，the following solutions

satisfy Eq．（20）．Therefore，from Theorem 3，we get

Of course，we can also obtain the higher－order adiabatic invariants．

Example 2 Let us consider the extreme value for the following fractional problem of the calculus of variations

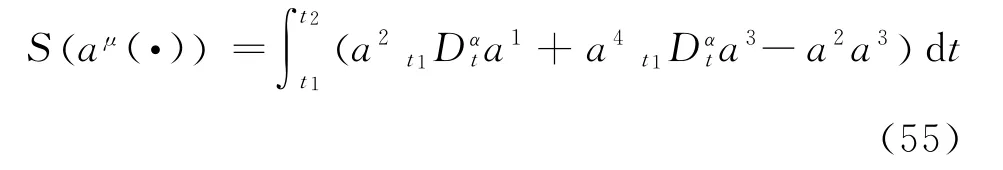
The problem （Eq．（55））is a fourth order Pfaff－Birkhoff fractional problem of the calculus of variations in terms of Riemann－Liouville derivatives．From Eq．（55），we obtain that

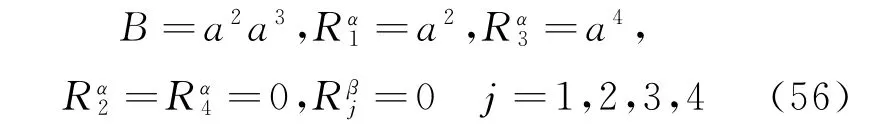
Obviously，the following solutions

satisfy the condition （32）．Then we can get the exact invariant from Eq．（34）that

Suppose the system （Eq．（7））is disturbed by the following small quantities

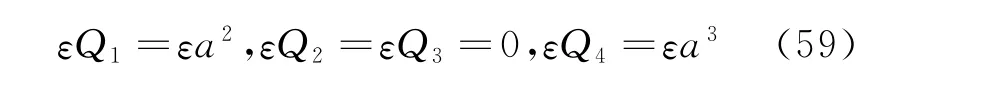
By some calculations，the following solutions

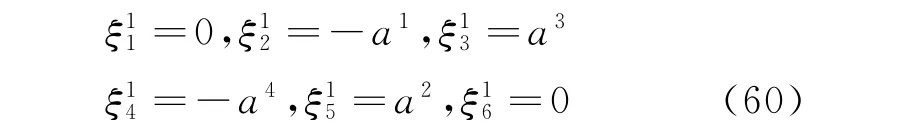
satisfy Eq．（41）．Hence，from Theorem 7，we get

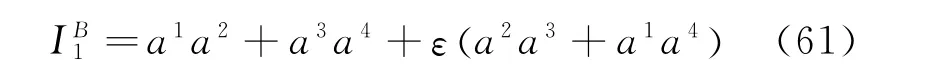
Of course，we can also obtain the higher－order adiabatic invariants．

4 Conclusions

In this paper，adiabatic invariants are studied for the fractional Lagrangian system and the fractional Birkhoffian system in the sense of Riemann－Liouville derivatives under the special and general infinitesimal transformations．We can also get adiabatic invariants in the sense of Caputo derivatives，Riesz－Caputo derivatives， Riesz－Riemann－Liouville derivatives and so on．Besides，much work deserves to do since adiabatic invariant and fractional variational problems are still in their early days．

Acknowledgements

This work was supported by the National Natural Science Foundation of China （Nos．11272227，11572212）and the Innovation Program for Postgraduate in Higher Education Institutions of Jiangsu Province（No．KYLX15＿0405）．

［1］ BURGERS J M．Die adiabatischen invarianten bedingt periodischer systems［J］．Annals of Physics，1917，357（2）：195－202．

［2］ ZHANG Y．A new type of adiabatic invariants for nonconservative systems of generalized classical mechanics［J］．Chinese Physics，2006，15（9）：1935－1940．

［3］ ZHANG Y，FAN C X．Perturbation of symmetries and Hojman adiabatic invariants for mechanical systems with unilateral holonomic constraints［J］．Communications in Theoretical Physics，2007，47（4）：607－610．

［4］ LUO S K．Lie symmetrical perturbation and adiabatic invariants of generalized Hojman type for disturbed nonholonomic systems［J］．Chinese Physics Letter，2007，24（24）：3017－3020．

［5］ JIANG W A，LUO S K．A new type of non－Noether exact invariants and adiabatic invariants of generalized Hamiltonian systems［J］．Nonlinear Dynamics，2012，67（1）：475－482．

［6］ JIANG W A，LI L，LI Z J，et al．Lie symmetrical perturbation and a new type of non－Noether adiabatic invariants for disturbed generalized Birkhoffian systems［J］．Nonlinear Dynamics，2012，67（2）：1075－1081．

［7］ ZHANG Y．Perturbation to Noether symmetries and adiabatic invariants for generalized Birkhoffian systems［J］．Bulletin of Science and Technology，2010，26（4）：477－481．（in Chinese）

［8］ CHEN J，ZHANG Y．Perturbation to Noether symmetries and adiabatic invariants for Birkhoffian systems based on El－Nabulsi dynamical models［J］．Acta Physica Sinica，2014，63（10）：104501．（in Chinese）

［9］ ZHANG Yi．Method of Jacobi last multiplier for solving dynamics equations integration of generalized classical mechanics system［J］．Journal of Nanjing U－niversity of Aeronautics ＆ Astronautics，2012，44（2）：262－265．（in Chinese）

［10］HILFER R．Applications of fractional calculus in physics［M］．Singapore：World Scientific，2000．

［11］MILLER K S，ROSS B．An introduction to the fractional integrals and derivatives－theory and applications［M］．New York：Wiley Inc，1993．

［12］SAMKO S G，KILBAS A A，MARICHEV O I．Fractional integrals and derivatives－theory and applications［M］．Yverdon：Gordon and Breach，1993．

［13］KILBAS A A，SRIVASTAVA H M，TRUJILLO J J．Theory and applications of fractional differential equations［M］．Amsterdam：Elsevier，2006．

［14］PODLUBNY I．Fractional differential equations［M］．San Diego：Academic Press，1999．

［15］OLDHAM K B，SPANIER J．The fractional calculus［M］．San Diego：Academic Press，1974．

［16］JESUS I S，MACHADO J A T．Fractional control of heat diffusion systems［J］．Nonlinear Dynamics，2008，54（3）：263－282．

［17］CHEN Y Q，VINAGRE B M，PODLUBNY I．Continued fraction expansion approaches to discretizing fractional order derivatives－an expository review［J］．Nonlinear Dynamics，2004，38（1／2／3／4）：155－170．

［18］RIEWE F．Nonconservative Lagrangian and Hamiltonian mechanics［J］．Physical Review E，1996，53（2）：1890－1899．

［19］RIEWE F．Mechanics with fractional derivatives［J］．Physical Review E，1997，55（55）：3581－3592．

［20］AGRAWAL O P．Formulation of Euler－Lagrange equations for fractional variational problems［J］．Journal of Mathematical Analysis and Applications，2002，272（1）：368－379．

［21］AGRAWAL O P．A general formulation and solution scheme for fractional optimal control problems［J］．Nonlinear Dynamics，2004，38（1／2／3／4）：323－337．

［22］AGRAWAL O P．Fractional variational calculus and the transversality conditions［J］．Journal of Physics A：Mathematical and General，2006，39（33）：10375－10384．

［23］AGRAWAL O P．Fractional variational calculus in terms of Riesz fractional derivatives［J］．Journal of Physics A：Mathematical and Theoretical，2007，40（24）：6287－6303．

［24］AGRAWAL O P．Generalized Euler－Lagrange equations and transversality conditions for FVPs in terms of the Caputo derivative［J］．Journal of Vibration and Control，2007，13（9／10）：1217－1237．

［25］AGRAWAL O P，MUSLIH S I，BALEANU D．Generalized variational calculus in terms of multi－parameters fractional derivatives［J］．Communications in Nonlinear Science ＆ Numerical Simulation，2011，16（12）：4756－4767．

［26］BALEANU D，AVKAR T．Lagrangian with linear velocities within Riemann－Liouville fractional derivatives［J］．Nuovo Cimento B，2004，119（1）：73－79．

［27］FREDERICO G S F，TORRE D F M．A formulation of Noether′s theorem for fractional problems of the calculus of variations［J］．Journal of Mathematical A－nalysis and Applications，2007，334（2）：834－846．

［28］MUSLIH S I，BALEANU D．Hamiltonian formulation of systems with linear velocities within Riemann－Liouville fractional derivatives［J］．Journal of Mathematical Analysis and Applications，2005，304（2）：599－606．

［29］ATANACKOVIC T M，KONJIK S，PILIPOVIC S．Variational problems with fractional derivatives：Euler－Lagrange equations［J］．Journal of Physics A：Mathematical and Theoretical，2008，41（9）：095201．

［30］HERZALLAH M A E，BALEANU D．Fractional order Euler－Lagrange equations and formulation of Hamiltonian equations［J］．Nonlinear Dynamics，2009，58（1）：385－391．

［31］JARAD F，ABDELJAWAD T，BALEANU D．Fractional variational optimal control problems with delayed arguments［J］．Nonlinear Dynamics，2010，62（3）：609－614．

［32］ALMEIDA R，TORRES D F M．Necessary and sufficient conditions for the factional calculus of variations with Caputo derivatives［J］．Communications in Nonlinear Science ＆ Numerical Simulation，2011，16（3）：1490－1500．

［33］HERZALLAH M A E，BALEANU D．Fractional Euler－Lagrange equations revisited［J］．Nonlinear Dynamics，2012，69（3）：977－982．

［34］ZHOU S，FU J L，LIU Y S．Lagrange equations of nonholonomic systems with fractional derivatives［J］．Chinese Physics B，2010，19（12）：120301．

［35］ZHOU Y，ZHANG Y．Fractional Pfaff－Birkhoff principle and fractional Birkhoff′s equations in terms of Riemann－Liouville derivative［J］．Bulletin of Science and Technology，2013，29（3）：4－10．（in Chinese）

［36］ZHOU Y，ZHANG Y．Fractional Pfaff－Birkhoff principle and Birkhoff′s equations in terms of Riesz fractional derivatives［J］．Transactions of Nanjing U－niversity of Aeronautics and Astronautics，2014，31（1）：63－69．

［37］SONG C J，ZHANG Y．Perturbation to Noether symmetries and adiabatic invariants for generalized Birkhoff systems based on El－Nabulsi dynamical model［J］．Transactions of Nanjing University of Aeronautics and Astronautics，2015，32（4）：421－427．

［38］ZHANG Y，LONG Z X．Fractional action－like variational problem and its Noether symmetries for a nonholonomic system［J］．Transactions of Nanjing University of Aeronautics and Astronautics，2015，32（4）：380－389．

［39］ZHOU Y，ZHANG Y．Noether′s theorems of a fractional Birkhoffian system within Riemann－Liouville derivatives［J］．Chinese Physics B，2014，23（12）：124502．