Compressive Sensing Sparse Sampling Method for Composite Material Based on Principal Component Analysis
2018-05-25,,1,2,,
, , 1,2,,
1.Jiangsu Engineering Centre of Network Monitoring,Nanjing University of Information Science and Technology,Nanjing 210044,P.R.China;
2.Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology,Nanjing University of Information Science and Technology,Nanjing 210044,P.R.China;
3.School of Computer and Software,Nanjing University of Information Science and Technology,
Nanjing 210044,P.R.China;
4.School of Information and Control,Nanjing University of Information Science and Technology,Nanjing 210044,P.R.China
0 Introduction
Principal component analysis (PCA)is one of the most commonly used multivariate statistical techniques[1]It uses an orthogonal mathematical transformation to convert the observed values of a set of possible dependent variables to principal components,the values that are not linearly related .The number of principal components is less than or equal to the number of original variables.Only when the data is combined with normal distribution,the principal component is independent from each other.PCA is sensitive to the cor-relation level between the original variables.It is also known as Hotelling transform,discrete KLT transform or proper orthogonal decomposition in different fields.
By projecting the data into the low dimensional space and obtaining the most possible features of the original data,PCA can be used to deal with the data of high dimension,noisy and high correlation.So far it has developed into a kind of exploratory data analysis and prediction model in terms of feature extraction using covariance or correlation matrix decomposition or using a set of matrix signal values.In recent decades,scholars have looked into the characteristics of PCA extraction and dimension reduction in different disciplines[2-4].Wold et al.[5]used cross examination to determine the number of PCA principal components,and a PCA-method for model prediction.Ku[6]introduced"time lag transfer"to statistical monitoring,and developed the monitoring method of the previous static PCA to a dynamic PCA method,which was applied to the detection of the disturbance of the dynamic multivariable system.
As long as the signals are sparse,through the sampling rate of compressive sensing (CS)is far lower than that of the traditional Nyquist sampling theorem[7-9].The theory must be premised on the sparsity of the signal,and PCA can be used for data dimensionality reduction.Masiero et al.[10]used PCA to find transformations to sparsify signals for CS to retrieve.They dynamically adapted non-stationary real-world signals through the online estimation on their correlation properties in space and time,and then utilized PCA to to derive the transformations for CS.Li et al.[11]proposed an adaptive block compressive sensing based on edge detection at the encoder,and a smoothed projected Landweber (SPL)reconstruction algorithm based on principal component analysis at the decoder.The reconstruction algorithm used PCA to train a dictionary adapting to image structure with hard thresholding,thus the image blocking effects were eliminated effectively and the reconstructed image quality was improved.Dietz et al.[12]presented a real-time dynamic image reconstruction technique, which combined CS and PCA to achieve real-time adaptive radiotherapy with the use of a linac-magnetic resonance imaging system.Li et al.[13]proposed an efficient image fusion framework for infrared and visible images on the basis of robust principal component analysis(RPCA)and CS.Compared with several popular fusion algorithms,this framework could extract the infrared targets while retaining the background information in the visible images.
Therefore,the compressive sensing method based on PCA is proposed to provide a better so-lution to sparse data representation problem of huge amount of ultrasonic phased array signal.
1 Principal Component Analysis
PCA is to reduce the dimension of the original data space by constructing a new set of latent variables,and then extract statistical features from the mapping space,therefore to understand the spatial characteristics of the original data.The variables of the new mapping space are composed of linear combination of the original data variables,which greatly reduces the dimension of the projection space.The number of new variables is less than that of the original variables,while still carry useful information of the original data as much as possible.Its contents include the definition and acquisition of main elements,as well as the principal component of the data reconstruction.Since the statistical characteristic vectors of the projection space are orthogonal to each other,the correlations between variables are eliminated,and the complexity of the original process characteristic analysis is simplified.Therefore,this method can effectively identify the most important elements and structures in the data,remove the noise and redundancy,reduce the original complex data,and reveal the simple structure behind the complex data.
Given the original datax= (xij)N×M,xis standardized to eliminate the dimensional effects,and the expression is shown as
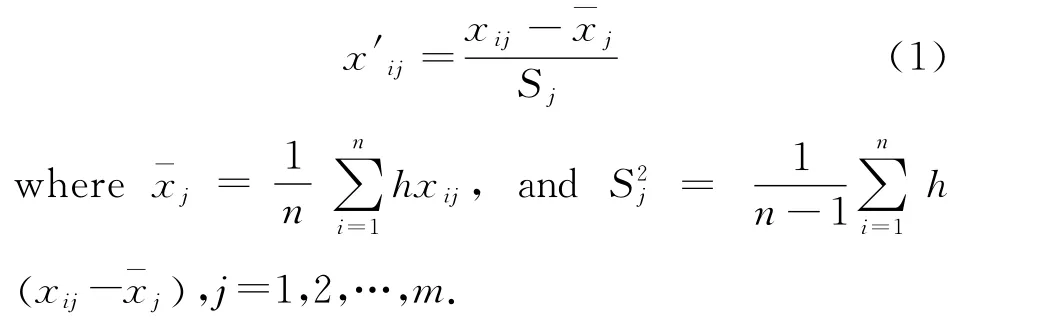
The correlation coefficient matrix is calculated between the data variables after standardized operation,and the covariance matrixRis
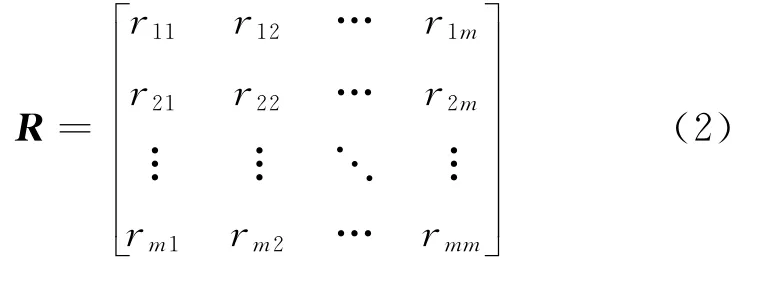
where the elementrjkrepresents the correlation coefficient of the original variablex′jandx′k,andrjk=rkj,shown as

Jacobi method is used to solve the character-istic equationand the eigenvalues of the covariance matrix and the corresponding eigenvectors are obtained.Then it is sorted according to the size of the order,and the characteristic value is recorded as[λ1,λ2,…,λm],and the corresponding feature vector is recorded as[p1,p2,…,pm]
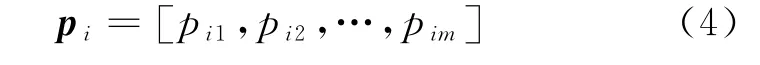
Then the main elements are calculatedti=Xpi,where the principal componenttion behalf of the projection of the data matrixxon the direction of the load vector corresponding to the main element.
The contribution rate of each principal com-ponents is calculated asas well as the cumulative contribution rate1,2,…,m.
In general,the 1th,2th,kth principal component corresponding to the eigenvalues ofλ1,λ2,…,λkwill be selected,where the cumulative contribution rate of eigenvalues is between 85%and 95%.
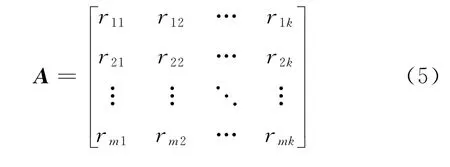
In addition,according to the needs,the corresponding dimension (that is,the number of principal components)is selected to composition of the transformation matrix
Finally,the new data after dimension reduction is calculated as

2 Compressive Sensing Method Based on PCA
CS is a novel theory of sampling and restoration for sparse signal[7-9].As long as the original signals are sparse in the time domain or under some kind of orthogonal transform,the signals can be sampled in a low sampling rate,and the original signals can be reconstructed with high probability.
2.1 Sparse representation of signals
CS is based on the premise that the signal must be sparse.When sparsifying the signals,the appropriate sparse transform base according to the signal characteristics is necessary to be selected.
Suppose an originalxsignal with the length ofN,the number of signal isM,aN×Mdimension matrix can be constructed with the original signal,because there are mutual relationship between the amplitude of each signal in each time point.According to the principal component analysis,the covariance matrix obtained ofN×Ndimension can be used as the sparse transform base for sparse representation of signal.Then,the original signalxcan be expressed as
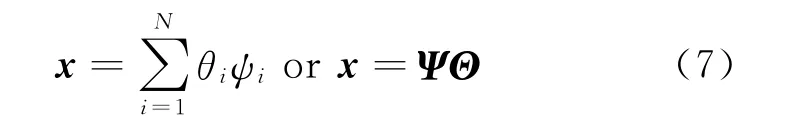
whereΨ= [ψ1,ψ2,…,ψN]is the transformation matrix ofN×Ndimension,Θthe sparse coefficient vector obtained byxaccording to the principal component analysis,and must meet the following formula
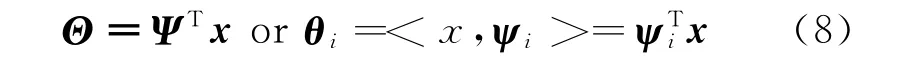
PCA reduces a kind of high dimensional data to low dimensional data.Then,a set of new variables in low dimensional replace the original variables in high dimension satisfies the conditions associated with the original ones.Therefore,the new variables can carry the maximum information of the original ones.PCA can be used to make sparse representation of the signals.Compared with the commonly used sparse representation method,the sparse signals obtained by the proposed method is more closely related to the original signals.
According to Section 1,the sparse coefficient vector of original signal is calculated as

whereΨis the transformation of matrixAin Section 1.
2.2 Projection observation of signals
The core of the compressive sensing theory is to design the measurement matrix,and directly determine whether the compressive sensing can be implemented successfully.If the signalxhas a sparse representation under an orthogonal transformΨ,a measurement matrixΦ,Ψ∈RM×N,which is not related to the transform baseΨ,and a linear measurement ofMdimension can be obtained

Suppose the production measurement vector isy=[y1,y2,...,yM],then
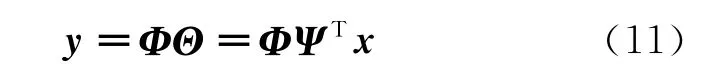
In order to restore the original signal with high probability,the production measurement matrixΦ,which is not related to the sparse transform baseΨand satisfied with the restricted isometry property,is needed to be constructed to make production transformation of the signal.Gauss random measurement matrix is not related to the majority of the fixed orthogonal base and satisfies the restricted isometry property,so the Gauss matrix can be used as the projection observation matrix[14-16].For the ultrasonic phased array signal,the Gauss random measurement matrix is multiplied with the sparse coefficient of the phased array signal,and the observation vector of the signal can be obtained.
Suppose the measurement matrixΦisM×Ndimension,andΦ∈RM×N,then the general term
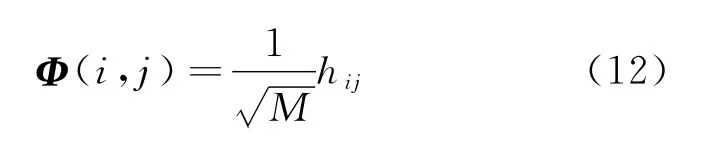
Each element in the matrix is independent to the Gauss distribution with the mean value of 0,and the varianceThis matrix is not relat-ed to the vast majority of sparse signals,and requires less measurement values in the reconstruction.Gauss random measurement matrix is a matrix with very strong randomicity but high uncertainty.For a signal with a length ofNand a sparse degree ofK,onlyM≥cKlogmeas-ured values are needed to recover the original signal with high probability,wherecis a very small constant.
2.3 Sparse reconstruction of signals
During the process of compressive sensing,reconstructing the signalxfrom the observationsyis the inverse problem related to compression sampling,and is called signal reconstruction.By solving Eq.(11),the reconstructed signal can be obtained.This problem is underdetermined with infinite solutions.Candes et al.proved that the underdetermined problem can be solved by solving the minimuml0-norm[13],that is,
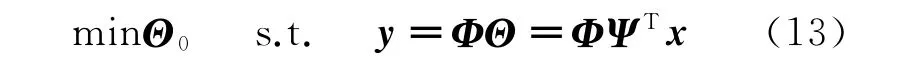
Eq.(13)is a linear programming problem,and is also a convex optimization problem.Taking the reconstruction error into account,it is converted into a minimuml1-norm problem as

During the process of signal reconstruction,convex optimization algorithm and greedy iterative algorithm are commonly used[17-18].One kind of algorithm is based on convex optimization,mainly by increasing the constraint to obtain the sparsest.And commonly used algorithms are basis pursuit algorithm and gradient projection sparse reconstruction algorithm.The other kind of algorithm is based on greedy iterative algorithm,mainly by the combination of local optimization method to find the non-zero coefficients,in order to approach the original signal.Commonly used algorithms are matching pursuit algorithm and orthogonal matching pursuit algorithm.
3 Experiment and Results
A composite plate is the experimental object.There are nine piezoelectric elements in the linear array arranged on the plate with an equal interval of 12mm.In signal acquisition,data collection points are 1 024,and sampling frequency isfs=1 000 000Hz.
One array element is set as a drive to transmit signal,and the other eight elements as the sensor to receive the reflection signal.Each array element stimulates the signal in turns,then each degree corresponds to 9×8signals,and 9×8×181sets of data can be obtained.The 90°direction of the data emitted by No.0array element and received by No.1array element is selected as the experimental data,and the processing method of other angles is consistent with this.The time domain waveform of the data set is shown in Fig.1.
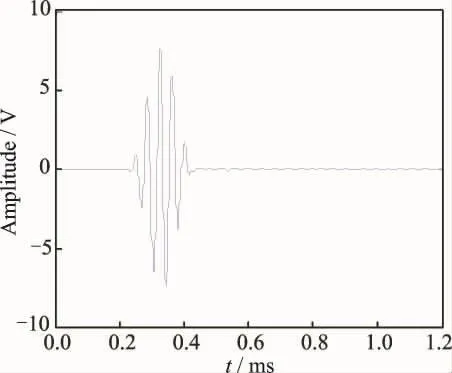
Fig.1 Waveform of original signal in time domain
At first,PCA is used to deal with the waveform obtained by the 90°direction of the phased array signal emitted by No.0array element and received by No.1array element.The sparse representation of the original signal is obtained,as shown in Fig.2.It can be seen that the sparse coefficient of the phased array signal after PCA transform is mostly zero or close to zero,which is consistent with the characteristic of sparse signal.
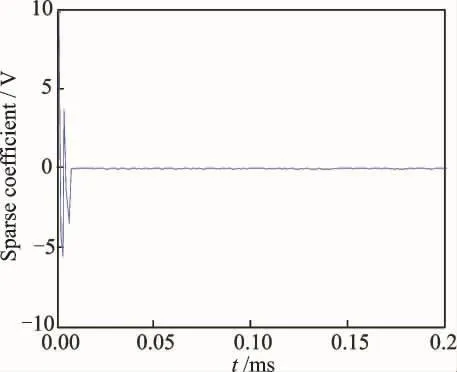
Fig.2 Sparse coefficient after principal component analysis
Then,the length of utrasonic phased array data isN=1 200,and the number of observationsM=400is selected to complete the operation of signal projection observation,and the waveform is shown in Fig.3.
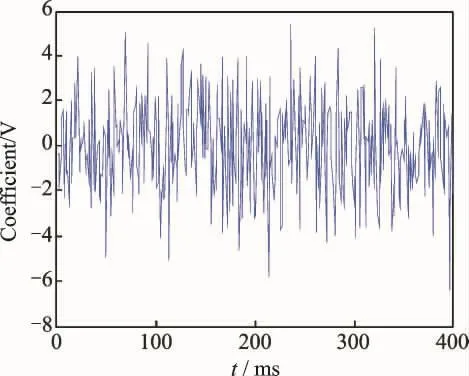
Fig.3 Signal obtained by projection observation
Finally,the basis pursuit algorithm is used to deal with the ultrasonic phased array signal,and the reconstructed signals obtained are shown in Fig.4.
4 Experimental Error Analysis
The reconstructed signal based on orthogonal matching pursuit algorithm has some differences in the signal waveform,compared with the original phased array signal.In order to analyze the effect of the reconstruction algorithm more accurately,the reconstructed error with different reconstruction algorithm is displayed numerically,as shown in Table 1.The absolute errorΔVand the relative errorδare calculated as below
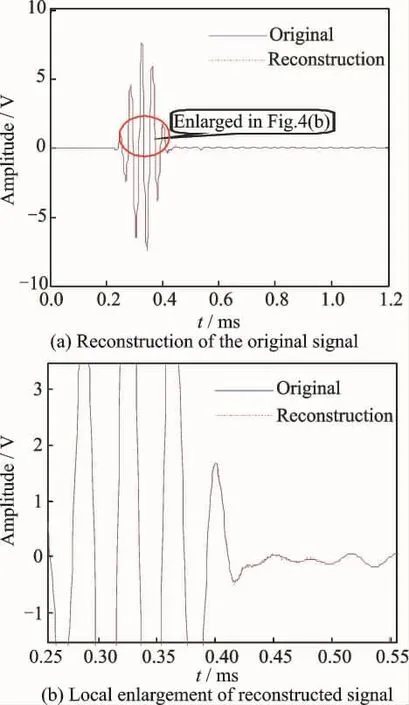
Fig.4 The signal reconstruction based on basis pursuit algorithm
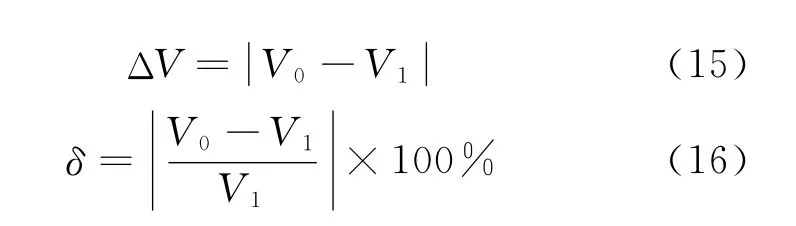
whereV0is the amplitude of reconstructed signal at the point of maximum amplitude deviation,andV1the amplitude of original phased array signal at the same point.
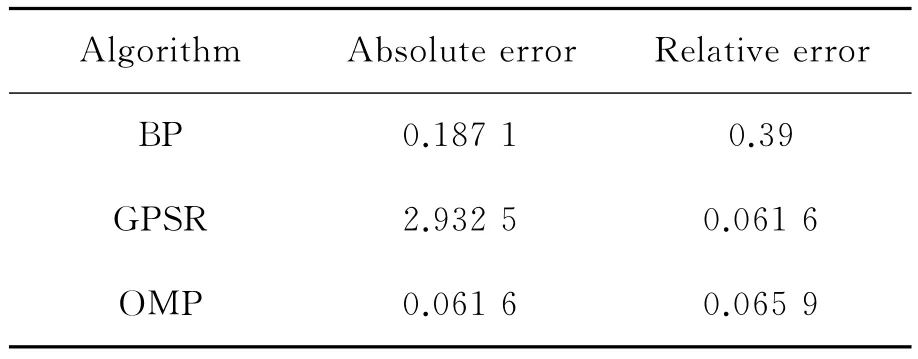
Table 1 Reconstruction error
In Table 1,GPSR is gradient projection for sparse reconstruction algorithm,and OMP is orthogonal matching pursuit algorithm.Fig.5shows the reconstructed signal obtained by BP,GPSR and OMP,respectively.
Table 2shows the error comparison of some common transform base and the principal component analysis method.
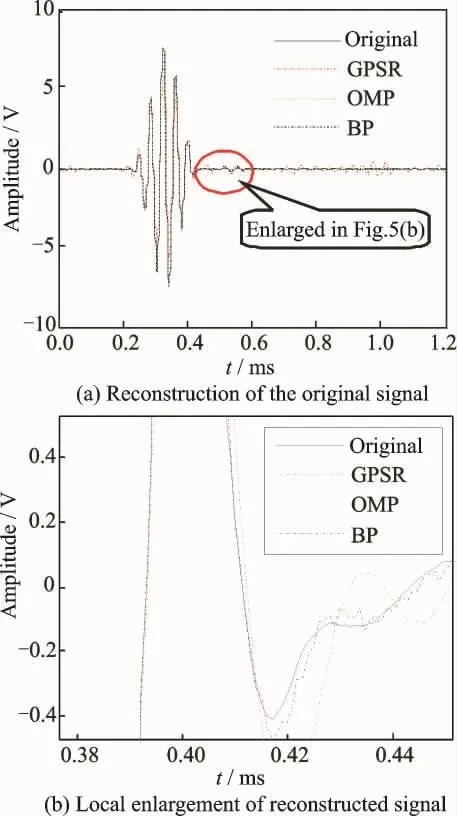
Fig.5 The signal reconstruction based on BP,GPSR and OMP
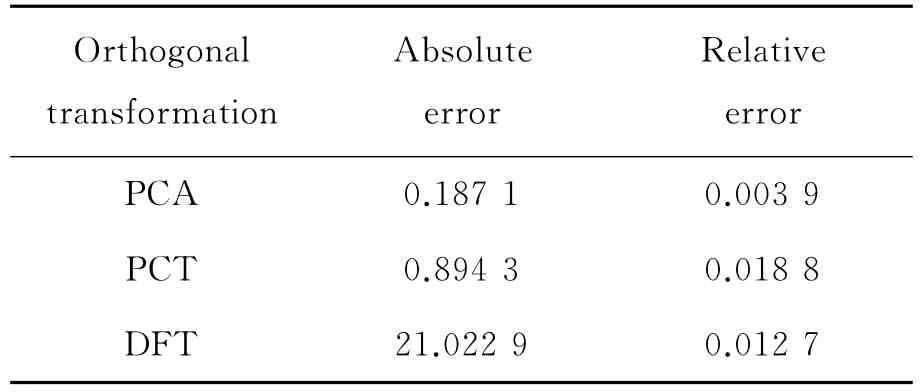
Table 2 The error comparison
In Table 2,DCT is discrete cosine transform,and DFT is discrete fourier transform.
The analysis of experimental error indicates that the relative error is relatively lower than that of commonly used method.That is,the proposed method can be applied to signal sparse representation of compressive sensing.
5 Conclusions
This paper studies the compressive sensing sparse sampling method based on PCA.This method not only solves the difficulty in storage and processing due to the large amount of data obtained by ultrasonic phased array structural health monitoring,but also effectively improves the relationship between the original signal and the signal after sparse representation.And the experimental result shows that PCA can be used to reconstruct the signal obtained from the phased array structure health monitoring after sparse representation of the signal with small reconstruction error.In future research,we can choose more optimized projection observation matrix,and more efficient reconstruction algorithm to reconstruct the ultrasonic phased array signal.
Acknowledgements
This work is supported by the National Natural Science Foundation of China(Nos.51405241,61672290),and the Jiangsu Government Scholarship for Overseas Studies and the PAPD Fund.
[1] LIU S,GU G,ZHANG Q,et al.Principal component analysis algorithm in video compressed sensing[J].International Journal for Light and Electron Optics,2014,125(3):1149-1153.
[2] MASIERO R,QUER G,MUNARETTO D,et al.Data acquisition through joint compressive sensing and principal component analysis[C]∥IEEE Conference on Global Telecommunications.USA:IEEE,2009 :1271-1276
[3] ZHANG Y,XU C,LI C,et al.Wood defect detection method with PCA feature fusion and compressed sensing[J].Journal of Forestry Research,2015,26(3):745-751.
[4] SINGH A,SHARMA L N,DANDAPAT S.Multichannel ECG data compression using compressed sensing in eigenspace[J].Computers in Biology &Medicine,2016,73:24-37.
[5] WOLD S.Cross-validatory estimation of the number of components in factor and principal components models[J].Technometrics,1978,20(4):397-405.
[6] KU W,STORER R H,GEORGAKIS C.Disturbance detection and isolation by dynamic principal component analysis[J].Chemometrics and Intelligent Laboratory Systems,1995,30(1):179-196.
[7] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[8] YIN H,LIU Z.Survey of compressed sensing[J].Control and Decision,2013,28(10):1441-1445.
[9] SUN Y J,GU F H.Compressive sensing of piezoelectric sensor response signal for phased array structural health monitoring[J].International Journal of Sensor Networks,2017,23(4):258-264.
[10]LI Ran, GAN Zongliang, ZHU Liangchang.Smoothed projected Landweber image compressed sensing reconstruction using hard thresholding based on principal components analysis[J].Journal of Image & Graphics,2013(5):504-514.(in Chiense).
[11]DIETZ B,YIP E,YUN J,et al.Real‐time dynamic MR image reconstruction using compressed sensing and principal component analysis(CS-PCA):Demonstration in lung tumor tracking[J].Medical Physics,2017,44(8):3978
[12]LI J,SONG M,PENG Y.Infrared and visible image fusion based on robust principal component analysis and compressed sensing[J].Infrared Physics &Technology,2018,89:129-139.
[13]CANDES E.The restricted isometry property and its implications for compressed sensing[J].C R Math Acad Sci Paris 2008,346(9-10):589-592.
[14]ZHANG B Y,CHEN H H,WANG R C,et al.New random signal generating method of multiple excitation vibration system based on white noises(in chinese)[J].Journal of Nanjing University of Aeronautics & Astronautics,2017,49(6):839-844.
[15]CHEN T,ZHU G,LIU Y.Optimization research of Gauss matrices in compressive sensing[J].Application Research of Computers,2014,31(12):3599-3602.
[16]QI M X,CHEN S J,ZHOU S P,et al.Crack Detection in Pipes with Different Bend Angles Based on Ultrasonic Guided Wave[J].Transactions of Nanjing University of Aeronautics and Astronautics,2017,34(3):318-325.
[17]LI Y,HE S.Blind signal separation algorithm for non-negative matrix factorization based on projected gradient[J].Computer Engineering,2016,42(2):104-107.
[18]ZHU Y,ZHU Y,PENG Y.Adaptive compressive sensing and tracking of dynamic sparse spectrum[J].Journal of Signal Processing,2016,32(3):341-348.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Simulation Tools for a Fiber-Optic Based Structural Health Monitoring System
- Segmentation of Thermographic Sequences in Frequency Modulated Thermal Wave Imaging for NDE of GFRP
- Non-destructive Evaluation of Absolute Stress in Steel Members Using Shear-Wave Spectroscopy
- Quantitative Rectangular Notch Detection of Laser-induced Lamb Waves in Aluminium Plates with Wavenumber Analysis
- Effect of Thermal Treatment on CFRP Parts Before and After Adhesive Bonding
- Full Wavefield Analysis for Damage Assessment in Composite Materials
