DNA折纸术在0-1整数规划问题中的应用
2018-05-25赵鑫月殷志祥巩成艳
赵鑫月,殷志祥, 巩成艳
(安徽理工大学数学与大数据学院,安徽 淮南 232001)
DNA折纸术是一种全新的DNA自组装的方法,与传统的DNA自组装相比,DNA折纸术更容易构造出高度复杂、结构稳定的纳米级结构,并具有可寻址性,是DNA自组装与DNA纳米技术领域的一个重大进展。DNA折纸术的基本原理是将一条较长的DNA单链(脚手架链)与一系列经过特殊设计的短的DNA片段(订书钉链)通过碱基配对原则进行互补,可控地构造出理想的纳米结构或图案。文献[1]首先提出了DNA折纸术这一概念并成功构造出各种相对比较复杂的纳米级形状和图案,包括方形、矩形、五角星、星形、笑脸以及美洲地图等若干种图案。文献[2]基于DNA折纸原理成功构造出中国地图,进一步证明DNA折纸术具有构造几乎任何复杂二维纳米级形状的能力。文献[3-4]研究了可精确调控三维曲面的立体花瓶结构,将DNA折纸术在结构设计与制造方面的研究推向高潮。文献[5]结合DNA纳米折纸术给出了一个用DNA纳米结构组装找出最短哈密顿路径的方法。文献[6]采用DNA纳米折纸结构编码信息,借助纳米结构之间的粘性末端进行自组装,给出了一种非确定性的图着色模型。
0-1规划问题作为整数规划问题的特殊形式,在运筹学中具有广泛的应用。许多NP完全问题也可以都可以转化为0-1规划问题。解决该问题的算法很多,有穷举法、隐枚举法、分支定界法等,但目前为止还没有很好的算法来完全解决该问题。文献[7]首次提出了在基于表面的DNA计算中采用荧光标记策略解决简单0-1规划问题的理论方案,尝试了DNA计算在规划问题中的应用。文献[8-10]分别将DNA芯片技术、DNA链置换技术、分子信标等运用于0-1规划问题,提出了相应的DNA计算模型。本文利用DNA折纸术对0-1规划问题提出了一种新的计算模型,利用杂交后初始数据链的长度的变化来实现对每一个约束条件的判断,求出问题的可行解。
1 0-1整数规划问题的数学模型
0-1整数规划是整数规划的特殊情形,其变量仅取值0或1。文中利用DNA计算解决的0-1整数规划问题,是指派问题的推广。
max(min)z=c1x1+c2x2+…+cnxn
下面讨论所对应的0-1整数规划问题的算法:
步骤1生成给定问题的变量取值为0或1的所有可能组合;
步骤2利用每一约束条件剔除非可行解(保留可行解);
步骤3生成剩余的解;
步骤4重复进行步骤2~3,可排除所有的非解,得到问题的所有可行解;
步骤5比较各可行解对应的目标函数值,进而得到最优解。
2 生物操作
步骤1
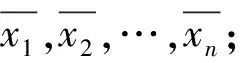
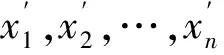
步骤2

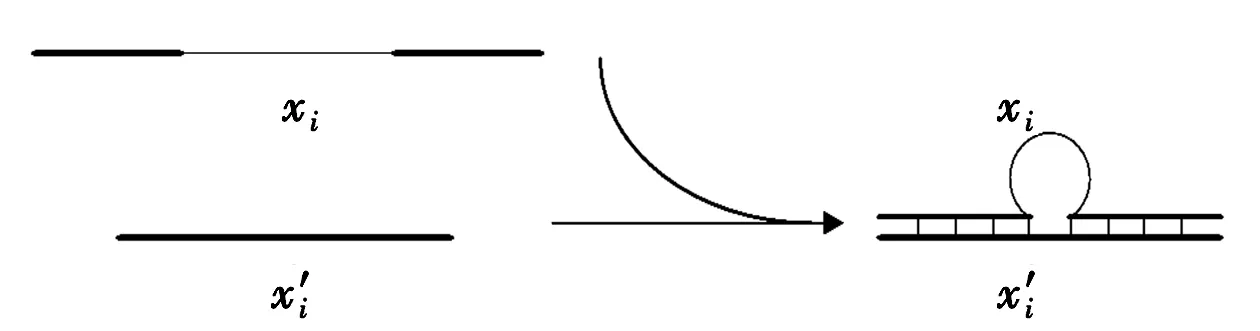
图1 xi和碱基互补形成发夹结构
步骤3
对满足约束方程的DNA链加热二级结构重新打开,再次通过凝胶电泳将短的DNA链分离出去。
步骤4
重复步骤2和步骤3(m-1)次,就可得到满足约束方程的可行解。
步骤5
对可行解所对应的目标函数值加以比较后,即可找到问题的最优解。
3 算法的实例分析
minu=2x+3y+z

步骤1


图2 初始数据池中所有DNA链的组合
2)构造3种分别与x,y,z的第一部分和第三部分互补的短的DNA链记为x′,y′,z′(见图3)。

图3 变量的编码
步骤2
对于第一个约束方程,往溶液中加入足量的x′,y′,z′,短的DNA链x′,y′,z′与8条长的DNA链中含有x,y,z部分的寡聚核苷酸片段发生杂交反应,即x′,y′,z′的前4个碱基对x,y,z的第一部分固定,后4个碱基对x,y,z的第三部分固定形成二级结构(见图4)。通过凝胶电泳分离出长度大于30+2Δx个碱基的DNA链和短的DNA链。得到满足条件的DNA链:1,2,3,5。

图4 加入满足约束方程一中变量的特殊补链
步骤3
加热将短的DNA链和长的DNA链分离,再通过凝胶电泳分离短的DNA链,此时溶液中只含有4种长的DNA链。
步骤4
对于第二个约束方程,在步骤3所得的产物中加x′,z′(见图5),分离出长度小于36+Δx的DNA链和短的DNA链,得到满足该条件的DNA链:2,5。通过加热、凝胶电泳操作,分离出短的DNA链。对于第三个约束方程,再在溶液中加入x′,y′(见图6),分离出长度小于36+Δx的DNA链和短的DNA链,得到满足条件的DNA链:2。

图5 加入满足约束方程二中变量的特殊补链

图6 加入满足约束方程三中变量的特殊补链
步骤5
对于本问题可行解仅有DNA链2,对应的编码变量值(1,1,0)也是最优解,目标函数的最小值为5。
4 结论
0-1规划问题有着广泛的应用和研究意义,本文用DNA折纸术的方法求解了0-1整数规划问题,通过构造订书钉链,使其对反应溶液中脚手架链的特定位置固定形成二级结构。根据反应后DNA链构形的变化对每一个约束方程进行判断,删除所有不满足条件的解,得到最优解。由于DNA折纸术的应用该方法能够产生大批量的高质量的纳米结构,并且对脚手架链和订书钉链的相对化学计量要求不高,实验操作简单,具有巨大并行性和高存储量的优点。更重要的是利用凝胶电泳操作使的每一步都可以排除大量非解,进一步降低了计算的时间复杂度和空间复杂度。但是当变量较多时,初始数据池中可能会由于编码问题脚手架链内部形成二级结构。因而,用脚手架链进行自组装,必须进行序列优化。随着分子生物学及生物工程的发展,该方法的进一步扩展有可能解决一般的整数规划问题。
参考文献:
[1] ROTHEMUND P W.Folding DNA to create nanoscale shaps and paterns[J]. Nature, 2006,400(7 082): 297-302.
[2] QIAN L L,WANG Y,ZHANG Z,et al.Analogic China map constructed by DNA[J]. Chines Science Bulletin,2006,51(24): 2 973-2 976.
[3] HAN D,PAL S,NANGREAVE J,et al. DNA origami with complex curvatures in three-dimensional space[J]. Science, 2011, 332(6 027):342-346.
[4] HAN D,PAL S,YANG Y,et al. DNA gridiron nanastructures based on four-arm junctions[J]. Science,2011,339(6 126):1 412-1 415.
[5] 俞洋, 苏邵, 晁杰. 基于DNA折纸术设计哈密特路径问题的解决方案[J].中国科学化学, 2015,45(11): 1 226-1 230.
[6] 俞洋, 苏邵, 晁杰. 基于DNA折纸术设计图着色问题的解决方案[J].南京大学学报,2016,52(4):656-661.
[7] 殷志祥, 张凤月, 许进. 0-1规划问题的DNA计算[J].电子与信息学报,2003,25(1): 62-66.
[8] 殷志祥, 许进. 分子信标芯片计算在0-1整数规划问题中的应用[J]. 生物数学学报, 2007,22(3): 559-564.
[9] 许进, 周康, 覃磊. 0-1规划问题的闭环DNA算法[J]. 系统工程与电子技术, 2009,31(4):947-951.
[10] 任晓玲, 白雪, 刘希玉. 基于三链DNA结构的0-1整数规划改进研究[J]. 计算机应用研究, 2013,30(1):56-59.
[11] 董亚飞.基于DNA链置换和荧光标记的0-1规划问题的计算模型[J].数学的实践与认识,2013,43:153-158.
[12] 张凤月, 殷志祥, 许进. DNA芯片在0-1规划问题中的应用[J]. 生物化学与生物物理进展, 2003, 30(3): 412-415.
[13] 杨进. 基于抗原中介三链DNA结构的0-1整数规划[J]. 计算机工程与应用, 2008,44(2):76-79.
[14] FEI L,JIN X,ZHANG L. DNA computing model based on self-assembled nanoparticle probes for SAT problem [J]. Advanced Materials Research,2012,443-444: 513-517.
[15] DUNN K E,DANNENBERG F,TE OULDRIDGE,et al. Guiding the folding pathway of DNA origami[J].Nature,2015,525(7 567): 82-86.
[16] SHEN X,SONG C,WANG J,et al. Rolling up gold nanoparticle-dressed DNA origami into three-dimensional plasmonic chiral nanostructures[J]. Journal of American Chemical Society,2012,134(1): 146-149.
[17] MARINI M,PIANTANIDA L,MUSETTI R,et al. A revertible,autonomous,self-assembled DNA origami nanoactuator[J]. Nanor letters, 2015,11(12): 5 449-5 454.
[18] CASTRO C E. A primer to scaffolded DNA origami[J]. Nature Methods, 2011,8(3):221-229.
[19] FUNKE J,DIETZ.Placing molecules with Bohr radius resolution use DNA origami[J]. Nature Nanotechnology, 2016,11(1):47-52.
[20] 钱璐璐. DNA自组装在分子计算和纳米技术等方面应用的研究[D]. 上海: 上海交通大学,2007.
