基于修正KMV模型的商业银行信用风险度量研究

王 佳，黎 晗

（东北大学秦皇岛分校 经济学院，河北 秦皇岛 066004）

引言

信用风险是目前我国金融市场面临的主要风险之一。2016年银监会公布的数据显示，到2016年末我国商业银行不良贷款余额高达15123亿元，比上个季度末多了183亿元。导致这一现象的一个重要原因就是，上市公司信用违约风险的增加。因此，引入适用于我国的信贷风险度量方法，对上市公司的信用风险进行系统的度量和预测，及时预防和控制各公司信用违约的发生，进而维护我国整个经济体系的安全，是当前迫切需要解决的问题。

目前，国际上采用的信用风险度量方法主要包括两种：一种是传统度量方法，主要包括5C模型、Z值评分模型和ZETA模型等。研究表明，传统模型主观性较强，风险评估结果的准确性较低，且存在时滞等问题。另一种是现代度量方法，主要包括J.P摩根银行的信用矩阵Credit Metrics模型、CSFP的CreditRisk+模型、麦肯锡公司的信贷组合观点Credit Portfolio View以及KMV公司的KMV模型。其中，由于KMV模型可以直接利用股票市场数据计量信用风险、利用资本市场信息来预测公司违约风险，使得KMV模型的应用最为广泛。Duffie等（2004）认为，在计算预期违约率方面，KMV模型具有很强的预测能力[1]。Kollár等（2015）将 Merton 模型、Credit Metrics模型、KMV模型和Credit Risk+模型进行比较分析，结论表明，KMV模型主要利用股票市场中的资产价值和波动性作为变量，更方便应用于公开交易的公司，且KMV模型考虑了不同的负债种类和违约形式，更符合实际[2～3]。同时，一些学者对KMV模型进行修正研究，主要表现为对KMV参数中的违约点进行改进。Lee（2011）提出一种新的遗传算法，来求解最优KMV模型的违约点[4]。Zhang和Shi（2016）在PSOKMV模型引入模糊聚类思想，改进违约点的设定规则，结果表明，改进后的模型能够找到最优的违约点[5]。

国内学者对现代信用风险度量模型的研究起步较晚，主要集中于检验模型在我国金融市场中的适用性，并对金融机构的信用风险进行度量。较具代表性的有，曹道胜和何明升（2006）分别对 Credit Metrics模型、KMV 模型、Credit Portfolio View模型和Credit Risk+模型在中国商业银行的适用性进行分析，得出四种模型对中国信用风险管理都有一定的借鉴意义[6]。凌江怀和刘燕媚（2013）以10家上市商业银行为研究对象，运用KMV模型度量银行的信用风险，并检验KMV模型在中国商业银行信用风险度量中的适用性[7]。姚德权等（2015）以16家上市商业银行为样本，引入资产价格变结构点非参数检验方法，利用变结构KMV模型对商业银行的信用风险进行度量[8]。蒋彧和高瑜（2015）利用KMV模型，对2014年2月中国全部上市公司的信用风险进行评估[9]。

由于发达国家的市场经济环境和我国经济环境存在很大差异，国外上市公司发生违约的情况与我国的情况也可能存在差别。为了更好地考察KMV模型在我国市场评估上市公司违约风险的能力，本文对KMV模型中违约点的设定方法进行修正，并利用修正的KMV模型分别对处于同一行业的ST股和绩优股的信用风险进行度量。进一步对两类上市公司的信用风险估计结果进行非参数检验，包括Mann-Whitney U检验和双样本Kolmogorov-Smirnov检验，检验在一定显著性水平下，两类公司是否存在显著差别。

一、构建修正的KMV模型

KMV模型认为，一个上市公司的股权价值可以看作一个欧式看涨期权，标的资产是公司的总资产，行权价为公司债务价值。在债务到期日，如果公司的资产价值高于债务价值，则公司股权价值为公司资产价值与债务值之间的差额，公司履行债务；反之，则公司以其资产价值来偿还债务，股权价值变为0，当公司资产价值下降至某一临界值时，企业就会对其债务违约。因此，KMV模型的基本思想是借鉴Black-Scholes定价理论和Merton的期权定价思想，分析公司资产的未来市场价值到违约点的距离和预期违约概率来判断该公司的信用情况，该模型的具体参数（如表1所示）。

表1 KMV模型参数

利用KMV模型度量信用风险的具体步骤为：

第一步，确定上市公司的股权价值VE。中国上市公司股票被分割为流通股和非流通股。而非流通股没有市场交易价格，本文以每股净资产来估算非流通股的价格，即：

第二步，确定上市公司的债务账面价值VD。

第三步，确定上市公司的股权价值波动率δE。利用历史波动率法估计上市的公司股权价值波动率δE。首先，用Si表示第i天股票收盘价格，假设股票价格的对数服从正态分布，那么股票的日收益率为μi=ln（Si/Si-1）；然后，由股票日收益率μi可以求得股票日收益波动率δ，即其中最后，用股票日收益波动率δ计算股票的年收益波动率 δE，即其中，N为股票的年交易天数，N=一年总天数-节假日天数-公休日天数-停牌日天数。

第四步，确定股价年波动率δE与资产波动率δA之间的关系。令Δ为避险比率，存在关系式由伊藤引理得，股价年波动率δE与资产波动率δA之间的关系可以表示为：

第五步，确定公司资产价值VA与公司资产波动率δA。根据B-S期权定价模型，得到在时到期日T时公司市场价值和负债账面价值之间的关系为：

其中

为了计算 VA和 δA，将式（3）和式（4）联立起来：

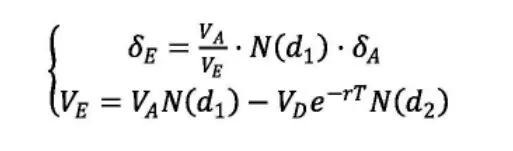
在该方程组中，已知量为 VA、VD、δE、r、T，未知量即需求解的量只有VA和δA，可以用 Matlab软件来求解这个方程组。

第六步，求违约点DPT。KMV公司提出违约点的设定表达式为DPT=STD+0.5LTD。为了更好地考察KMV模型在我国市场评估上市公司违约风险的能力，本文在借鉴KMV公司的研究经验基础上，结合国内学者的研究成果，对违约点的设定方法进行改进，表达式为：

第七步，求解违约距离DD。违约距离表示违约点和公司资产价值之间的距离，表达式为：

第八步，通过理论公式计算预期违约率EDF。在连续时间下，公司资产价值的对数遵循布朗运动，假设当t=0的时公司资产的市场价值为VA，则在t时刻公司资产的价值可以表示为：

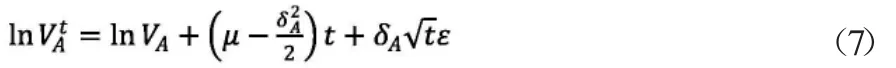
其中，μ为公司资产收益率的期望值，ε为该收益率的随机因子。

则公司的预期违约概率为：

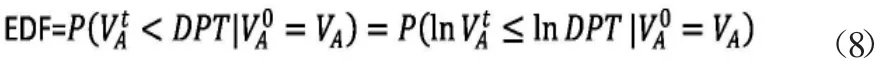
联立式（7）和式（8）两式可得：

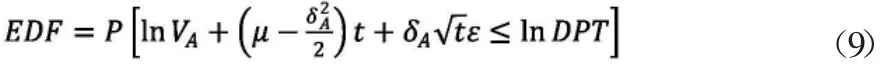
经过推导，得到：

二、实证研究

利用修正KMV模型，对不同行业上市公司ST股和绩优股的信贷风险分别进行度量，以KMV模型中违约距离指标来分析贷款质量。进一步对两类上市公司的信用风险估计结果进行非参数检验，包括Mann-Whitney U检验和双样本Kolmogorov-Smirnov检验，检验在一定显著性水平下，两类公司是否存在显著差别。

（一）样本和数据选取

为了使实证结果更加使人信服，排除不同交易市场（如H股市场）可能会对最后的实证结果产生的影响，本文将选择在我国A股市场选取样本上市公司，且选取来自不同行业上市公司的ST股和绩优股，使数据在不同行业的ST股与绩优股之间可以进行对比。根据以上选取样本原则，选取的上市公司样本（见表2）。

本文将选取以上10家上市公司股票在2016年10月10日至2017年1月20日（其中去掉因节假日停牌的天数）连续100个交易日的开盘价、最高价、最低价以及收盘价数据，上市公司的流通股和非流通股股数，上市公司的短期流动负债和长期非流动负债数据。数据来源于万德数据库和同花顺交易软件。

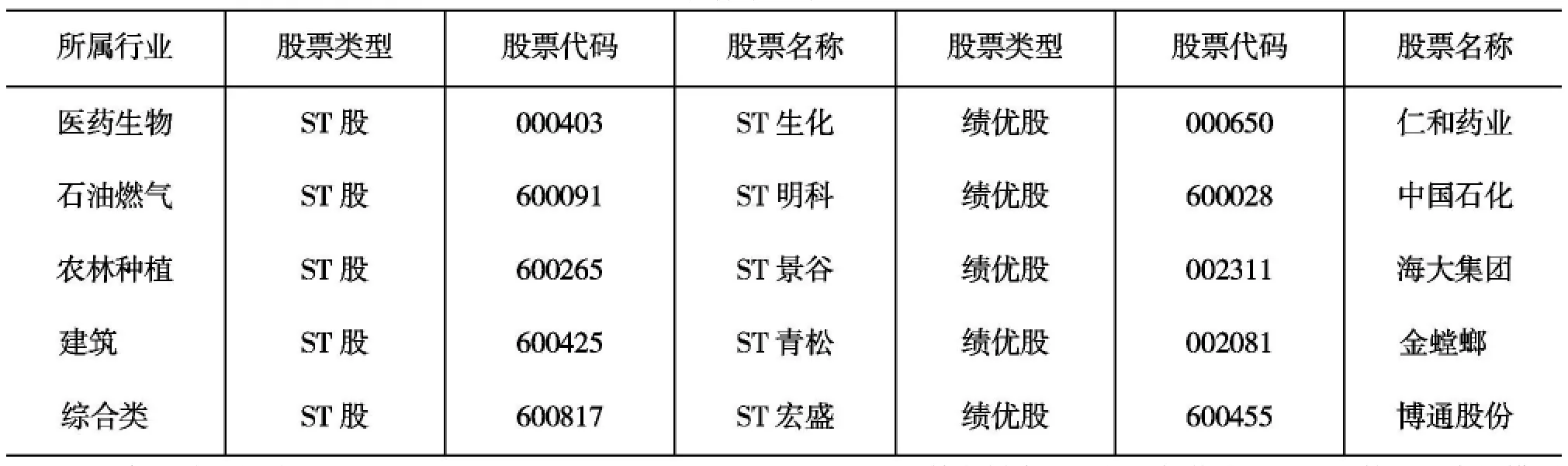
表2 各样本上市公司

（二）实证过程与结果

设各样本公司的债务期限取值为一年，即T=1，无风险利率为央行制定的一年期定期存款利率，即r=1.5%。按照第二节构建修正的KMV模型中的模型步骤，得到以下实证过程及结果。

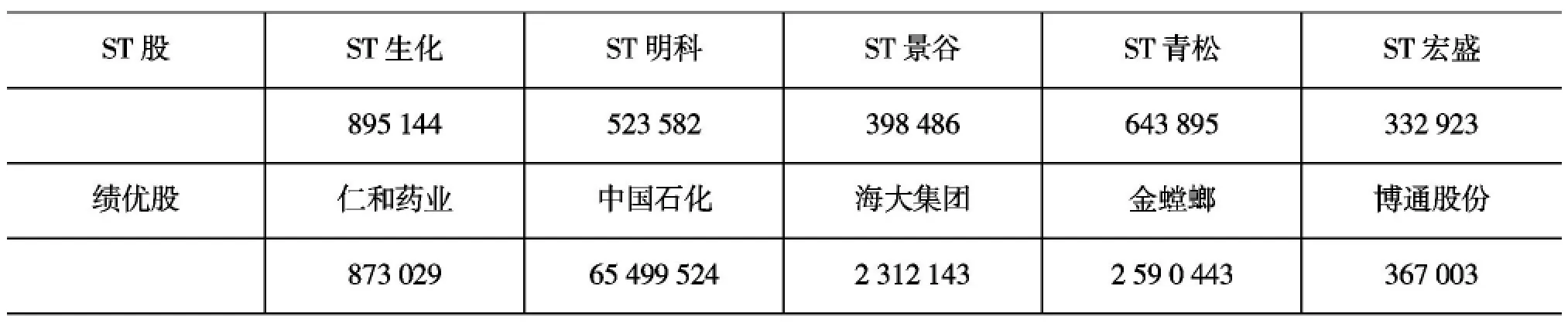
表3 样本公司股权市值 （单位：万元）

1.计算各样本公司的股权价值VE。根据第二节中的模型步骤1，假定流通股价格=非流通股价格=加权收盘价=（最高价+最低价+收盘价×2）/4。通过计算得到各样本公司的股权价值VE，结果（如表3所示）。

2.计算各样本公司的债务价值VD。根据第二节中的模型步骤2中的式（2）计算上市公司的债务价值VD，结果（如下页表4所示）。

3.计算上市公司股票价格年收益波动率δE。根据第二节中的模型步骤3，计算各样本公司的股票价格年收益波动率δE，结果（如下页表5所示）。

4.计算各样本公司的资产价值VA与资产波动率δA。根据第二节中的模型步骤5中的式（3）和式（4），利用Matlab软件，计算各样本公司的资产价值VA与资产波动率δA，结果（见下页表6）。

5.求各样本公司的违约点DPT。根据第二节中的模型步骤6中违约点的设定公式（5），得到各样本公司的违约点，结果（如下页表7所示）。

6.计算各样本公司的违约距离DD。将已求得的各样本公司的DPT、VA和δA值，代入第二节步骤7中的式（6），得到各样本公司的违约距离结果（见下页表8）。

根据上述实证结果，利用Excel软件做出样本公司的违约距离折线图（如本文图所示）。

7.计算各样本公司的预期违约率EDF。根据第二节步骤8中的式（10），得到各样本公司的预期违约率，结果（如下页表9所示）。

8.实证结果的显著性检验。分别对绩优股和ST股的违约距离和预期违约率结果进行非参数检验，包括Mann-Whitney U检验和双样本Kolmogorov-Smirnov检验。检验在5%的显著性水平下，两种上市公司的违约距离和预期违约率是否均具有显著差别，检验结果（见下页表10）。

表4 样本公司债务价值 （单位：万元）

表5 样本公司股票价格年收益波动率

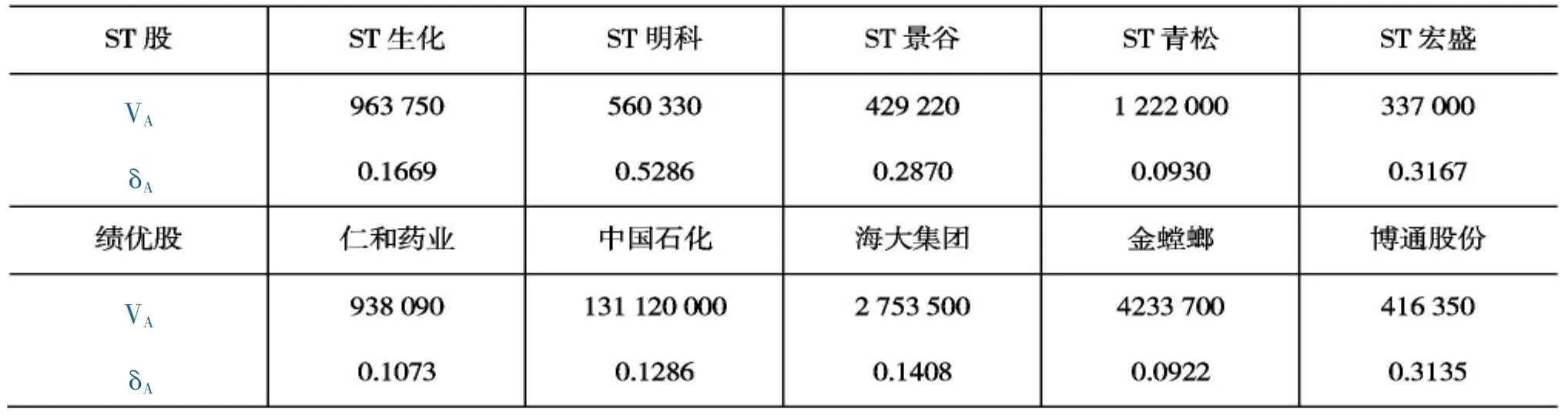
表6 样本公司的资产价值与资产波动率 （单位：万元）

表7 样本公司的违约点 （单位：万元）

表8 样本公司的违约距离

（三）结果分析

1.ST股和绩优股间的违约情况分析。从表6、表8和表9可以看出，在行业相同的条件下，五支ST股的股权波动率都明显大于绩优股的股权波动率，ST股的违约距离均小于绩优股的违约距离，同时ST股的预期违约率均大于绩优股的预期违约率。因此，绩优股在借贷资金过程中的违约风险小，ST股的违约风险大，得出的这个实证分析结果与事实是相符合的。由此可以得出结论，KMV模型度量信贷风险在我国的商业银行业是可行的，可以利用KMV模型通过一系列的计算得出上市公司的违约距离DD，通过分析违约距离来预测上市公司违约可能性，以此提高商业银行贷款质量。

2.行业间的违约情况分析。从下页图可以看出，医药生物和农林种植这两个行业下的两只上市公司股票的DD值之间的垂直距离比较大，而石油燃气、建筑和综合类这三个行业的股票违约距离之间的垂直距离相对来说比较小。通常，同一行业下的不同上市公司股票之间的DD值垂直距离越大，整个行业越景气，说明该行业下公司的运营好、业绩佳、利润高，一般就不太会发生违约。反之，违约的发生的概率就会比较高。因此，可以得出结论，某一行业的整体景气度在一定程度上会影响行业下所属上市公司的发展，商业银行在度量信贷风险时应该将借款企业所属行业景不景气这一点充分考虑进去，通常行业越景气，行业下所属企业的盈利能力越强，违约发生的概率就越小。

3.实证结果的非参数检验。从表10可以看出：（1）违约距离方面，Mann-Whitney U检验中，绩优股和ST股违约距离的Z值分别为2.456和2.657，且渐进显著性P值均为0。双样本Kolmogorov-Smirnov检验中，绩优股和ST股违约距离的Z值分别为2.789和2.754，且渐进显著性P值均为0。这说明，在5%的显著性水平下，绩优股和ST股的违约距离之间具有显著差别。（2）预期违约率方面，Mann-Whitney U检验中，绩优股和ST股违约距离的Z值分别为2.287和2.372，且渐进显著性P值分别为0.022和0.018，均小于显著性水平0.05。双样本Kolmogorov-Smirnov检验中，绩优股和ST股违约距离的Z值分别为2.441和2.247，且渐进显著性P值均为0。这说明，在5%的显著性水平下，绩优股和ST股的预期违约率之间具有显著差别。

各样本公司的违约距离图

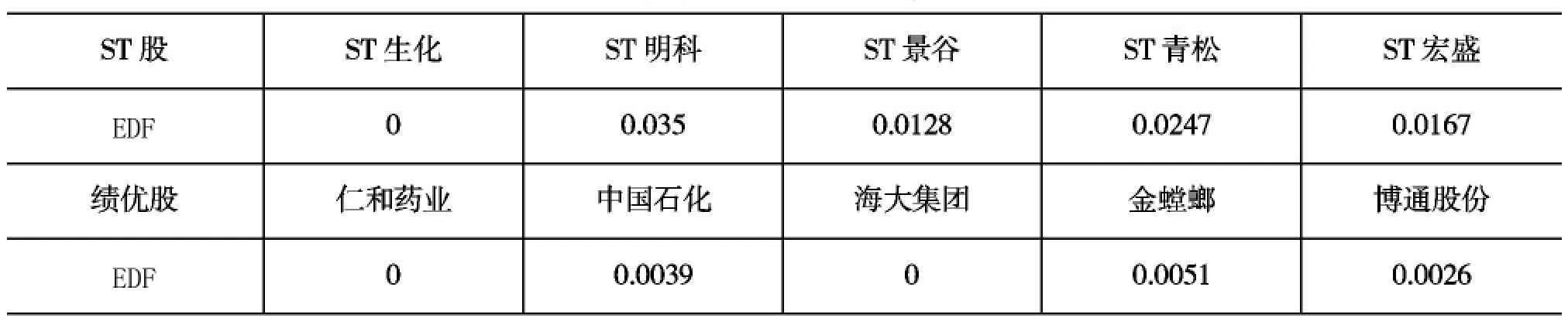
表9 样本公司的预期违约率

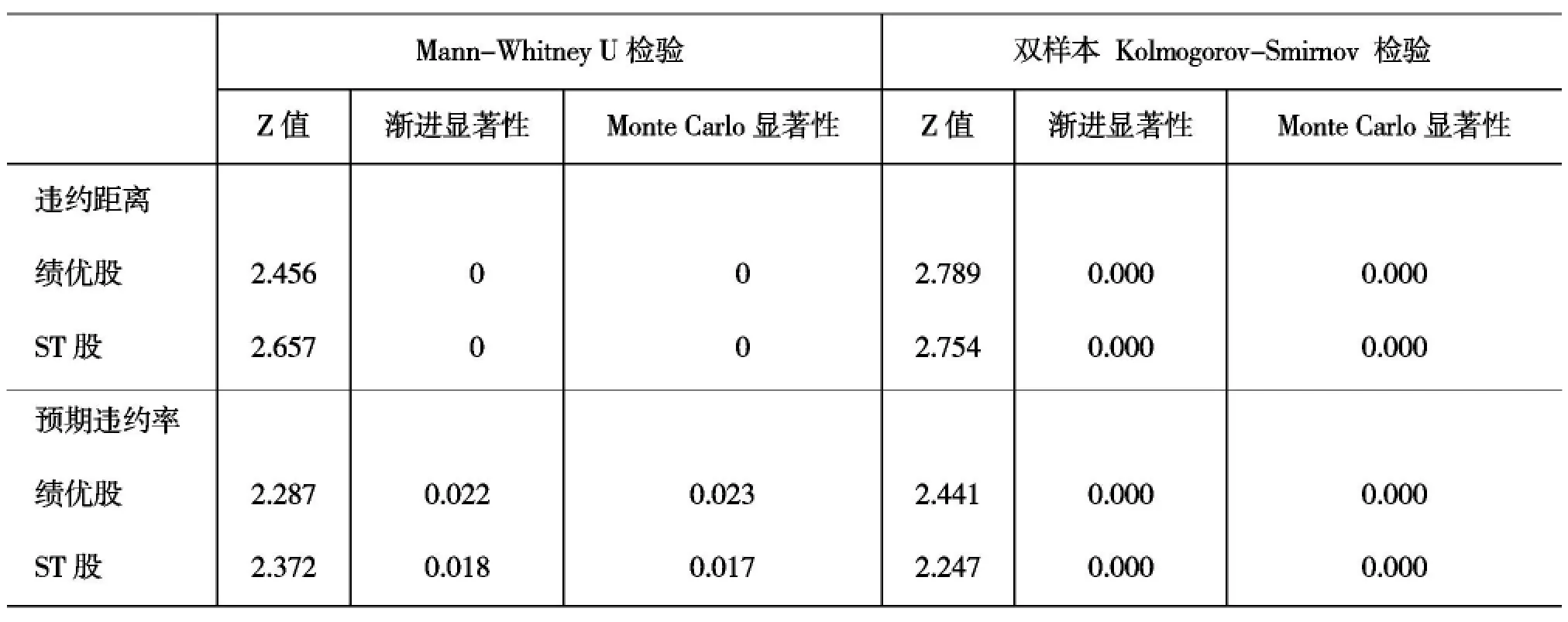
表10 绩优股和ST股违约距离和预期违约率的非参数检验结果

结语

本文根据中国金融市场的特点，对KMV模型中违约点的设定方法进行修正，利用修正后的KMV模型，对10家上市公司的信用风险进行评估，并对模型识别和预测信用风险的能力进行检验。得出结论：（1）相同行业下，ST股的违约距离均小于绩优股的违约距离，ST股的预期违约率均大于绩优股的预期违约率。同时，分别对绩优股和ST股的违约距离和预期违约率结果在5%的显著性水平下进行Mann-Whitney U检验和双样本Kolmogorov-Smirnov检验。结果表明，两种上市公司的违约距离和预期违约率均具有显著差别。这说明，修正后的KMV模型能够有效地评估中国上市公司的信用风险。（2）不同行业的发展景气程度不同，商业银行在度量信贷风险时应该将借款企业所属行业景不景气这一点充分考虑进去。通常，行业越景气，行业下所属企业的盈利能力越强，违约发生的概率就越小。

参考文献：

[1]Duffie D.，Wang K.Multi-period corporate failure prediction with stochastic covariates[J].Ssrn Electronic Journal，2010，(3)：635-666.

[2]Kollár B.，Weissová I.，Siekelová A.Comparative analysis of theoretical aspects in credit risk models[J].Procedia Economics and Finance，2015，(1)：331-338.

[3]Kollár B.，Gond?árová B.Comparison of Current Credit Risk Models[J].Procedia Economics and Finance，2015，(1)：341-347.

[4]Lee W.C.Redefinition of the KMV model’s optimal default point based on genetic algorithms—Evidence from Taiwan[J].Expert Systems with Applications，2011，(8)：107-113.

[5]Zhang Y.，Shi B.Non-tradable shares pricing and optimal default point based on hybrid KMV models：Evidence from China[J].Knowledge-Based Systems，2016，(1)：202-209.

[6]曹道胜，何明升.商业银行信用风险模型的比较及其借鉴[J].金融研究，2006，(10)：90-97.

[7]凌江怀，刘燕媚.基于KMV模型的中国商业银行信用风险实证分析——以10家上市商业银行为例[J].华南师范大学学报：社会科学版，2013，(5)：142-148.

[8]姚德权，张宏亮，黄学军.基于变结构KMV模型的商业银行风险承担度量研究[J].中国软科学，2015，(11)：109-122.

[9]蒋 ，高瑜.基于KMV模型的中国上市公司信用风险评估研究[J].中央财经大学学报，2015，(9)：38-45.