仿人体出汗比例的Walter暖体假人皮肤制备

师云龙， 钱晓明， 梁肖肖， 张文欢， 邓 辉， 王立晶， 范金土，2

(1. 天津工业大学 纺织学院， 天津 300387； 2. 康奈尔大学 人类生态学院， 纽约 14850)

暖体假人是一种从20世纪40年代逐步发展起来的生态学实验器械，到目前已经历了4代更新，最新一代暖体假人可模拟人体行走，攀爬等动作和出汗、呼吸等生理活动[1]。某些极端测试条件下不适合使用真人测试，同时由于个体差异的存在，真人测试的可重复性并不理想，因此暖体假人作为真人模拟器逐渐成为服装工效学研究中常见的一种设备[2]。

Walter出汗暖体假人是一款典型的第4代暖体假人，优势在于可同时测算出服装的热阻与湿阻2个在服装舒适性研究中极其重要的参数[3]。该假人全身出汗皮肤由具有相同透湿率的面料制成，即该假人全身各部位具有相同的出汗率，但是真实人体各部位的出汗率并不相同。为了使Walter出汗暖体假人实现人体出汗比例的目的，本文采用液体加成型硅胶，使用刮涂法制备出硅胶涂层，通过对涂层的透湿性能分析确定最佳涂层工艺，利用分形原理和硅胶涂层的热阻，湿阻，确定涂层的最佳涂覆方式，并制备非均匀出汗皮肤；之后对Walter暖体假人裸态与着装情况下采用2种出汗皮肤的整体热阻与湿阻测量结果进行比较分析。

1 实验部分

1.1 实验材料

加成型液体硅胶由东莞鸿风硅胶公司提供，由A、B 2种组分构成，将2种组分混合即可制得硅胶液。

Walter出汗暖体假人皮肤由天津戴米诺服装公司提供的面料制成，面密度为190 g/m2。

1.2 实验仪器

YG(B)216-Ⅱ型透湿箱(温州大荣纺织仪器有限公司)，YG606G型纺织品热阻湿阻测试仪(中国宁波纺织设备有限公司)，CP4202C型电子天平(上海奥豪斯有限公司)，DW-2型电动搅拌器(巩义英峪高科仪器厂)，DZF-6020型真空干燥箱(巩义市英峪高科仪器厂)。

1.3 硅胶涂层的制备

将液体加成型硅胶的A、B组分按照不同比例混合，搅拌10 min，混合均匀后置于真空干燥箱进行抽真空脱泡处理，脱泡完毕后使用刮辊将液体硅胶涂覆至皮肤面料内侧，静置于室温2 h，硅胶固化后涂层制备完成。通过调节硅胶组分的配比和刮涂的厚度，制备了质量比为1∶1,1∶3,1∶5和1∶7，涂层厚度分别为0.15、0.3、0.5、1 mm的涂层样品。

1.4 实验方法

通过对不同厚度和不同硅胶组分配比制备得到的硅胶涂层布进行透湿测试，确定涂层工艺。采用此涂层工艺制备具有分形结构的涂层布块，通过对比具有不同分形维数的涂层布块的热湿舒适性，确定最优涂层方式。使用该涂层方式按照真实人体出汗分布对Walter暖体假人原始皮肤进行刮涂，制得非均匀出汗皮肤，并对2款皮肤进行实验对比。

2 结果与讨论

2.1 硅胶涂层工艺的确定

本文实验采用YG(B)216-Ⅱ型透湿箱对硅胶样品的透湿性能进行测试，依据GB/T 12704.2—2009《纺织品 织物透湿性试验方法 第2部分：蒸发法》，设定箱内温度为(40±0.5)℃，相对湿度为(50±5)%。根据不同质量配比和不同涂层厚度制得的硅胶涂层布的透湿性能如表1所示。

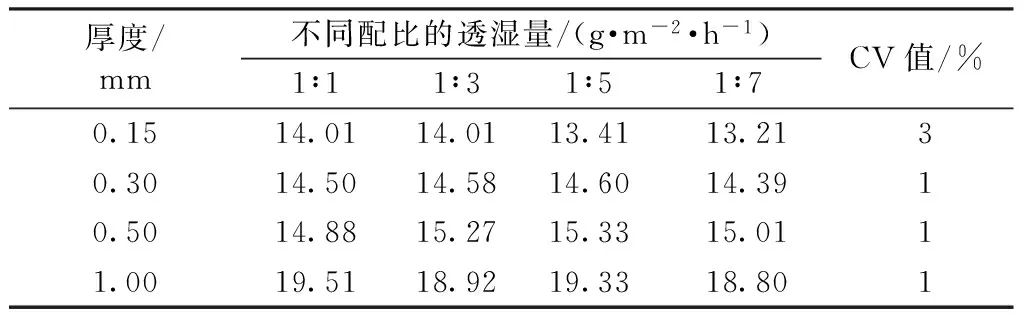
表1 不同质量配比和厚度的硅胶涂层透湿量Tab.1 Water vapor permeability of silicone coated samples of different mass ratios and thicknesses

由表1可知，在同一涂层厚度情况下，不同硅胶组分配比试样的透湿量变异系数均在5%以下，即硅胶涂层的透湿量与不同硅胶组分的配比无显著关系。在同一硅胶组分配比的条件下，随涂层厚度的增加，样品的透湿量均呈现增加的趋势。这是因为经脱泡处理的硅胶液内仍存在少量空气，在刮涂完毕等待固化的过程中，这部分空气从硅胶层中析出，形成孔洞，随硅胶层厚度的增加，孔洞的数量也在增多，直至形成允许水蒸气透过的通路，从而增加了硅胶层的透湿量。在本文实验中，硅胶层的作用是覆盖一部分皮肤的面积，减少被覆盖区域出汗量，以实现暖体假人皮肤的非均匀出汗，因此，硅胶涂层的透湿率应尽量小。故通过此透湿实验确定了硅胶涂层的工艺参数为：液体硅胶的A、B 2种组分的质量配比1∶1，硅胶层厚度0.15 mm。

2.2 硅胶涂层的分形结构

通过确定的硅胶层涂覆工艺，本文实验制备了3种具有分形结构的硅胶涂层布块，如图1所示。

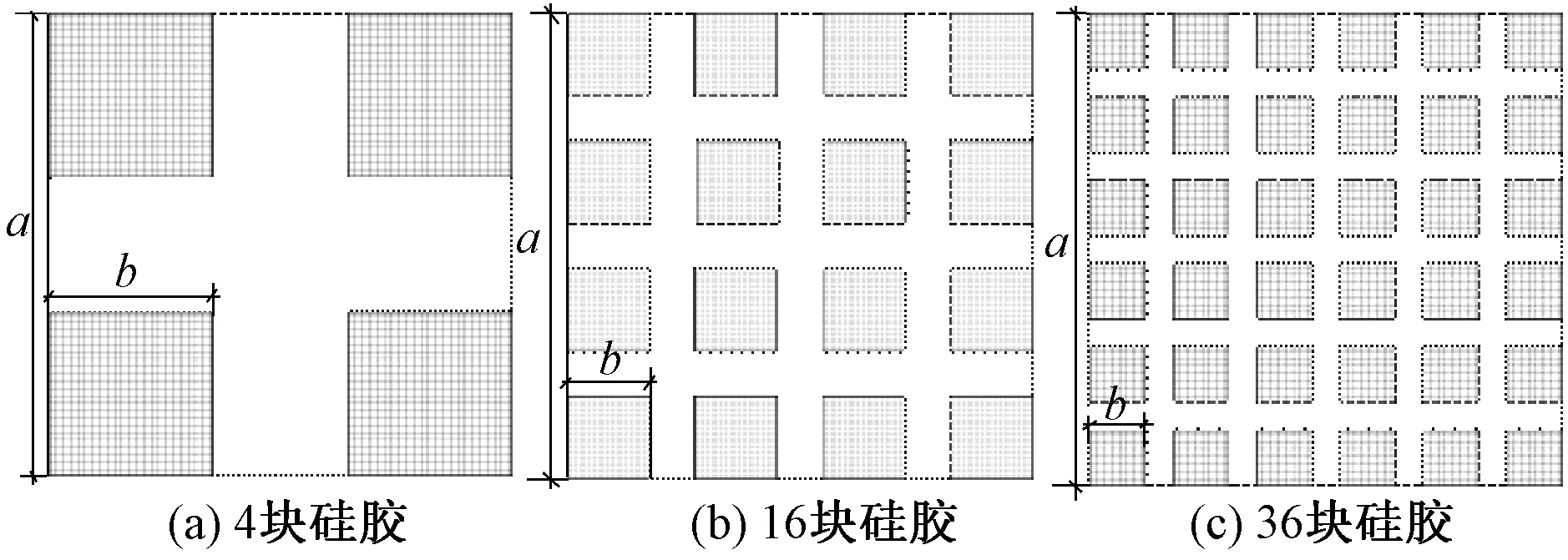
图1 硅胶块在面料上分布的示意图Fig.1 Distribution of silicone blocks on fabric. (a) 4 Silicone blocks; (b) 16 Silicone blocks; (c) 36 Silicone blocks

图1中，边长a为布块整体边长；b为硅胶块边长。3种涂覆方法的硅胶块总面积均为该布块总面积的50%。可看到，这3种面料样品均具有自相似结构，不同的自相似结构往往具有不同的分形维数，研究物体的分形维数有助于分析不同自相似结构物体的特殊性质。其分形维数为

Df=lgM/lgN

式中：M为某个试样上硅胶块的数量；N为布块边长与硅胶块边长之商。

图1(a)中，布块边长为32 cm，硅胶块边长为11.314 cm，布块边长与硅胶块边长之比N为2.828，根据公式计算，图1(a)中所示涂覆方法的分形维数为1.335。同理，图1(b)所示涂覆方法的分形维数为1,599；图1(c)所示涂覆方法的分形维数为1.675。

2.3 硅胶涂层的均匀性

本文实验对布面进行硅胶涂覆采用手工刮辊进行涂覆，由于人为用力可能存在不均匀，因此需要对涂覆完成的硅胶布块整体质量进行测量，以排除因硅胶涂覆质量不同带来的后续试验结果的不同。实验采用电子天平进行测量。其中，涂有4块硅胶块的面料质量为49.51 g，涂有16块硅胶块的面料质量为50.83 g，涂有36块硅胶块的面料质量为46.83 g，3种试样的变异系数为3.39%，处于合理误差范围之内，证明数据可信，说明在刮涂过程中不同试样上涂覆的硅胶量接近，质量因素对后续试样结果的影响可排除。

2.4 硅胶涂层布的热湿舒适性

面料的热阻(It)与湿阻(Re)是衡量面料热湿舒适性最重要的2个指标[5]。本文实验采用纺织品热阻湿阻测试仪对3种具有分形结构的硅胶涂层布的热阻与湿阻进行了测量，测试结果如表2所示。

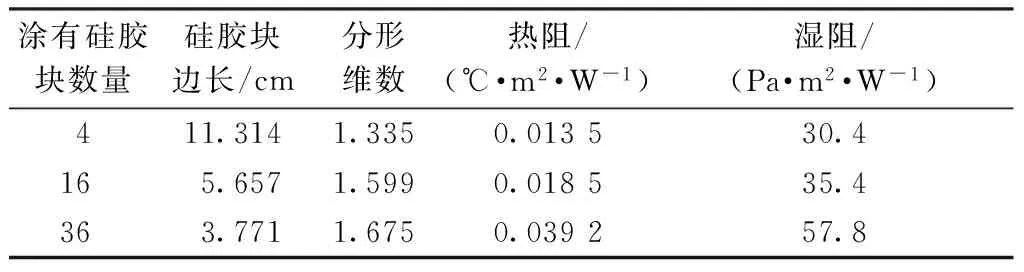
表2 不同硅胶涂层样品的热湿舒适性Tab.2 It and Re of different silicone coated samples

由表2可知，随硅胶块数量的增多，样品的热阻与湿阻均呈现出增加的趋势。热阻的增加表明出经处理的面料的保暖能力得到提升，提高了面料的热舒适性；同时湿阻的增加则降低了面料排湿的能力，降低了面料的湿舒适性，因此，在热阻与湿阻均呈现上升趋势的情况下，需在硅胶涂层面料的保暖性能与排湿性能之间取得平衡。根据ISO 9920—2007 《热环境下的人体工效学：服装整体热阻与湿阻》的评估，日常穿着服装的湿阻通常低于40 Pa·m2/W。湿阻过高时，面料内侧不能及时扩散至服装外环境的水汽会出现冷凝，导致服装微环境的湿度增加，破坏服装与人体的热湿平衡，给穿着者闷热的感觉，降低服装的穿着舒适性。本文实验中，涂有16块硅胶的涂覆方法可满足湿阻不高于40 Pa·m2/W同时热阻尽量高的需求，因此将涂有16块硅胶的涂覆方法确定为Walter出汗暖体假人非均匀皮肤的硅胶涂覆方法。

从表2中同样可看出，随硅胶块数量的增多，单个硅胶块的边长随之减少，同时，硅胶涂层的分形维数也在增加。前文确定的Walter出汗暖体假人非均匀出汗皮肤的最佳涂覆方法的分形维数为1.599，非常接近黄金分割数，1.618[6-7]。FAN[8]研究了羊毛的分型结构，发现羊毛的分形维数为1.595，非常接近黄金分割数。当羊毛的分形维数降低时，意味着羊毛趋向于实心而无法在高温环境中提供足够的散热能力；同时当羊毛的分形维数升高时则意味着羊毛趋向于空心，羊则会因羊毛无法提供足够的保暖能力而无法在低温环境生存。在本文实验中，硅胶涂层的分形维数理论上也有2个极端：0和2。当分形维数趋近于0时，意味着硅胶涂层不再具有分型结构，保暖能力不再有任何提升；当分形维数趋向于2时，说明在相同涂覆面积下，布面上的硅胶块数量也趋向于无穷大，同时面料的湿阻也随之增加，降低面料的湿舒适性。图1(b)所示的涂覆方法既可提升面料部分热舒适性，又可满足湿舒适性的要求，其分型维数接近于黄金分割数，也再一次证明了黄金分割数在现实生活中具有的丰富内涵。

2.5 非均匀与均匀出汗皮肤的比较

Walter出汗暖体假人非均匀皮肤的设计参考了Weiner提出的相对出汗强度的定义[9]。其定义相对出汗强度为身体某一部位出汗占人体全部出汗量的比例与该身体部位面积占人体全部表面积的比例之比。人体各部位出汗量参考了Havenith提出的人体出汗分布图[10]。本文实验将Walter的皮肤分为6部分，各部位的相对出汗强度如表3所示。

在本文实验中采用硅胶涂层的目的是隔绝出汗，在表1中可看出按照0.15 mm厚度进行涂层涂覆后硅胶涂层仍存在少量透湿量，但是在实际计算中，这部分透湿量是忽略不计的，也就是在后续计算时，按照硅胶涂层完全没有出汗量进行计算。

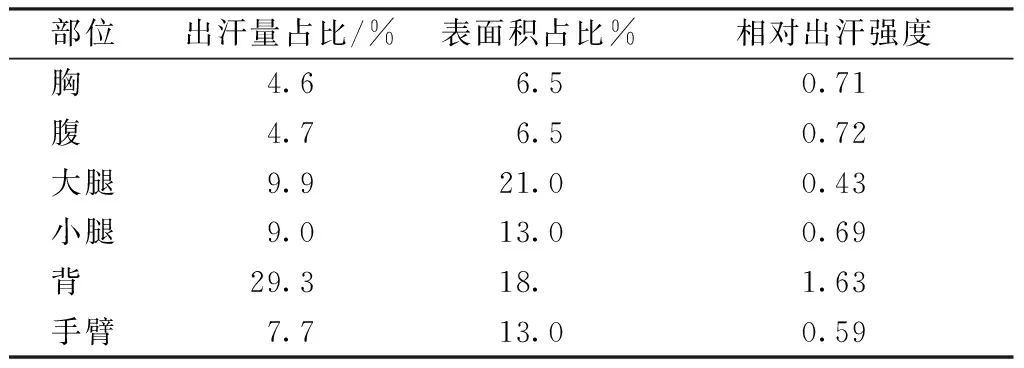
表3 Walter不同部位的出汗量、表面积及相对出汗强度Tab.3 Amount of sweat, surface area and relative sweating intensity of weating of different parts of Walter

由表3可看出，背部相对出汗强度最高，为1.63。为了方便计算，本文实验将背部相对出汗强度换算为1，其他部位的相对出汗强度则相应转换为：胸部，0.43；腹部，0.44；大腿，0.26；小腿，0.42；手臂，0.36。以胸部为例，其相对出汗强度为0.43，则意味着相对于背部，胸部的出汗强度为背部的43%，因此，在非均匀出汗的暖体假人皮肤上，假人的胸部部位的出汗强度应减少57%。胸部部位按照之前确定的硅胶涂覆工艺和刮涂方法，应该有57%的面积涂覆硅胶层。同理，假人腹部涂覆硅胶的面积为66%；大腿部位涂覆硅胶的面积为74%；小腿部位涂覆硅胶的面积为58%，手臂部位涂覆硅胶的面积为64%。

使用此涂覆规则制得的Walter出汗暖体假人的非均匀出汗皮肤与原始均匀出汗皮肤分别对Walter的裸态和着装状态的整体热阻与湿阻进行了测试。

暖体假人实验在人工气候室中进行，环境设定为温度为(20±0.5)℃，相对湿度为(65±5)%，风速为(0.3±0.1)m/s。着装测试前将整体服装放置于气候室内24 h进行调湿处理，测试时每次测量完毕都将服装脱下再穿上，重复测试3次。服装为普通工装套装，包含内衣，100%棉，205.21 g；长裤，100%棉，436.91 g；上装，100%棉，421.42 g。暖体假人裸态与着装状态热阻与湿阻的测量结果如表4、5所示。

表4 2种皮肤条件下的暖体假人裸态与着装热阻Tab.4 It of nude manikin and dressed manikin under two kinds of skin

由表4可看出，非均匀出汗皮肤装备状态下的测量结果与原始均匀出汗皮肤相比，热阻值均有提高。跟ISTM标准规定，整体式暖体假人裸态热阻值应在0.08～0.11 ℃·m2/W之间，因此，本文实验制备的非均匀出汗皮肤符合标准要求，测试结果可信。QIAN[11]在2004年使用完全不出汗的假人与正常出汗的暖体假人进行对比测试，结果显示2种状态下的假人裸态热阻值相差2%，这说明出汗量的变化对假人的干热损失没有影响。在本文实验中，均匀出汗皮肤与非均匀出汗皮肤的干热损失亦没有明显区别，在非均匀出汗皮肤的测试上出现了热阻值高于均匀皮肤的原因是非均匀皮肤内侧涂覆的硅胶层减少了皮肤的散热能力，增加了热阻，同时硅胶层的涂覆也阻止了部分水汽传递，较低的水汽蒸发减少了假人整体的湿热损失，这点也可从2种皮肤测试过程中不同的出汗量反应出来。2种皮肤测试过程中的出汗量如图2所示。

表5 2种皮肤的裸态与着装湿阻Tab.5 Re of nude manikin and dressed manikin under two kinds of skin

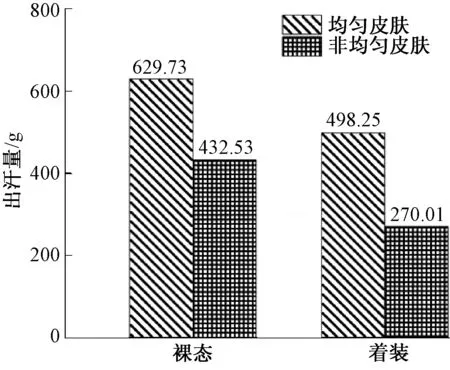
图2 不同状态的暖体假人使用不同皮肤的出汗量Fig.2 Sweat amount of two kinds of skin of Walter under different states

由图2可知，在裸态和着装状态下，非均匀出汗皮肤的出汗量均低于均匀出汗皮肤，这显然是因为非均匀出汗皮肤上涂覆的硅胶层阻碍了水蒸气的蒸发导致，这也验证了涂覆了硅胶的皮肤可实现暖体假人Walter的非均匀出汗。

由表5可知，在使用非均匀出汗皮肤的情况下，Walter暖体假人的裸态湿阻和着装状态湿阻均高于使用均匀出汗皮肤的状况。这种现象也与图2所示2种皮肤的出汗量变化有关。

根据湿阻的计算方法，出汗量的变化会极大改变假人的湿热损失，而湿热损失是影响湿阻计算的一个重要变量。从图2可看出，均匀出汗皮肤的出汗量均大于非均匀出汗皮肤，因此相同测试条件下，非均匀出汗皮肤情况下的湿热损失均低于均匀出汗皮肤，导致裸态和着装状态下的湿阻结果均大于均匀出汗皮肤。

3 结 论

1)采用不同组分配比制备的硅胶涂层透湿性能没有显著差异，硅胶涂层的厚度是决定其透湿率的关键因素，增加涂层厚度会增加涂层的透湿率，在本文实验中选择了0.15 mm作为涂层厚度。

2)具有不同分形维数的硅胶涂层在相同涂覆面积的前提下具有不同的热湿性能，分形维数越大，涂层布的热阻和湿阻都会增加。具有最接近黄金分割数的分形维数的涂覆方式可使硅胶涂层具有最佳热湿性能。

3)利用0.15 mm厚度和涂覆16块硅胶的方式制成的Walter出汗暖体假人非均匀出汗皮肤的裸态和着装状态的热阻与湿阻测量结果均大于原始均匀出汗皮肤。热阻增加的原因是硅胶涂层的存在降低了皮肤的散热能力；而湿阻增加的原因则是因为硅胶层降低了假人整体的湿热损失。

参考文献：

[1] FAN J, CHEN Y. Measurement of clothing thermal insulation and moisture vapor resistance using a novel perspiring fabric thermal manikin[J].Measurement Science and Technology, 2002, 13: 1115．

[2] HOLMÉR I. Thermal manikin history and appli-cations [J]. European Journal of Applied Physiology, 2004,92: 614-618.

[3] FAN J T, QIAN X M. New functions and applications of Walter, the sweating fabric manikin[J].European Journal of Applied Physiology, 2004, 92:41-644.

[4] MANDELBROT B B, WHEELER J A. The fractal geometry of nature[J]. Journal of the Royal Statistical Society, 1982, 147(4):468.

[5] WANG L J, QIAN X M. Engineering of High Performance Textiles [M]. Duxford, United Kingdom: Woodhead Publishing, 2017:217-299.

[6] WANG G, CHEN H, LV S, et al. Research on permeability of satin fabrics based on fractal theory[J]. Journal of Reinforced Plastics and Composites, 2015, 34(5): 377-387.

[7] WANG J Z,XI Z P, TANG H P, et al. Fractal dimension for porous metal materials of FeCrAl fiber[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(4): 1046-1051.

[8] FAN J, LIU J F, HE J H. Hierarchy of wool fibers and fractal dimensions[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2008, 9(3):293-296.

[9] WEINER J. The regional distribution of sweating[J]. The Journal of Physiology, 1945, 104:32-40.

[10] SMITH C J, HAVENITH G. Body mapping of sweating patterns in male athletes in mild exercise-induced hyperthermia[J]. European Journal of Applied Physiology, 2011, 111(7):1391-404.

[11] QIAN X M, FAN J T. Interactions of the surface heat and moisture transfer from the human body under varying climatic conditions and walking speeds[J]. Applied Ergonomics, 2006, 37: 685-693.