全要素生产率视角下供给侧结构性改革的经济增长效应——基于DSGE模型与PSTR模型的分析

刘金全, 张 龙

(1.吉林大学 数量经济研究中心, 吉林 长春 130012; 2.吉林大学 商学院, 吉林 长春 130012)

我国经济历经多年持续高速增长,目前已由“结构性加速”进入“结构性减速”阶段,原因可能在于我国长期沿用凯恩斯主义的“需求管理”宏观调控政策,造成投入的生产要素越多,经济运行效率越低的“供给结构”问题,长此以往,经济可能陷入“中等收入陷阱”,而跨越“中等收入陷阱”的关键是转换经济增长动力,使技术、创新、制度创造等为代表的新生产力要素成为我国经济跨越“中等收入陷阱”的主导力量。同时,2008年世界金融危机的爆发及事后影响迫使人们对宏观调控“需求管理”为主的经济思想展开反思,新常态下,面对复杂多变的国际经济形势,我国经济增长速度明显趋缓,经济结构调整处于攻坚阶段,如何更好地选择我国经济增长转型路径,顺利推进经济新常态发展是理论界和实务界需要攻关的课题。2015年末召开的中央经济工作会议为我国经济结构调整和发展动力转换指明了方向,供给侧结构性改革成为突破增长瓶颈的正确路径和跨越“中等收入陷阱”的有效保证,理论界和决策层对“供给管理”的宏观经济调控政策前所未有地重视。

一、文献综述和研究进展

从19世纪初“萨伊定律”的提出开始,“供给侧”经济学派大致经历了“萨伊定律→凯恩斯革命→供给学派→凯恩斯主义复辟→供给管理”这样的“螺旋式”历史演进过程,直至2008年金融危机爆发,“理性供给管理”的求真务实宏观调控思想得以确立经济地位,“供给侧结构性改革”是2015年末以来我国经济的热词,供给侧结构性改革的实施使学术界开始关注经济贡献供给侧思考改革与经济增长间的关系并试图分析改革的具体经济增长效应,大量学者对相关问题展开理论讨论与实证研究。

关于供给侧结构性改革与经济增长的理论分析:汪红驹等[1]认为结构性改革能显著提高全要素生产率,改善我国宏观经济运行状况,新常态下,结构性矛盾“倒逼”供给侧结构性改革。贾康等[2]通过对宏观经济调控“需求管理”为主的管理方式的反思,认为支撑我国经济长久发展的主要动力不在需求侧而在供给侧。洪银兴[3]认为拉动经济增长需要供给侧和需求侧协同发力,当下经济矛盾的主要方面来源于供给侧。刘伟[4]认为进入新常态的我国经济具有新变化、新挑战,使得经济失衡有了新特征,需求管理的宏观调控方式具有一定局限性,这种局限性要求引入供给侧结构性改革。金碚[5]的研究表明“三去一降一补”最终体现为劳动生产率的提高,供给侧结构性改革可以提高供给体系的协调性、高效性和高质性,促进实体经济增长。冯俏彬等[6]认为衡量我国供给侧结构性改革成功与否的主要标志是劳动力、资本、创新等要素形成的经济增长动力机制。方福前[7]的研究证实我国经济目前面临经济增速下行和通货紧缩并存的压力,表现为全要素生产率负增长、产能大面积过剩、库存增加,结构性改革方案是解决我国经济问题症结的有效途径。总体来看,关于供给侧结构性改革与经济增长的理论分析,学者大都在梳理我国经济运行态势尤其是新常态以来我国经济呈现出的一些“典型化”特征基础上,总结“需求管理”为主宏观调控方式的不足之处,提出供给侧结构性改革是改善我国宏观经济运行状况和解决“三期叠加”阵痛效应的有效途径。

关于供给侧结构性改革与经济增长的实证分析:徐朝阳[8]通过一个多部门的动态随机一般均衡模型(DSGE模型)理论推演与实证模拟得出一些经济领域存在的供给抑制政策是我国经济增速下滑的主要原因。王海军等[9]通过总需求-总供给模型(AD-AS模型)分析当下我国经济的主要矛盾,得出提高全要素生产率(TEP)、深化供给侧结构性改革可以实现经济长期稳定增长。余泳泽[10]通过对我国省际TEP进行再估算,得出考虑产能利用率后的纯化TFP得到明显提升,供给侧结构性改革可以解决由于TEP低下带来的产能过剩问题。马彪等[11]基于包含家庭、厂商、商业银行和中央银行四部门的DSGE模型分析我国企业产能水平和经济波动问题,得出供给结构失衡条件下的技术进步将引发过剩产能和经济失调,供给侧结构性改革对于去除过剩产能、产业转型升级至关重要。徐晋[12]通过构建供给侧结构方程,指出技术创新、制度供给价值是维持经济增长的有效保证,全面解析了经济增长、要素投入与供给侧结构性改革。从上述文献的研究视角和模型方法看,关于供给侧结构性改革与经济增长的实证分析,多数学者基于供给侧结构性改革的内涵,使用AD-AS和DSGE模型等方法分析供给侧结构性改革的经济增长效应,得出供给侧结构性改革能够有效改善投资结构并提高要素生产率,解决我国经济产能过剩、要素使用效率低下等问题,供给侧结构性改革有利于我国经济持续稳定发展。

梳理已有文献发现,理论界与学术界普遍认同经济的结构性改革能促进经济增长,但多数文献为理论或实证的单一论证,实证研究较少且缺乏理论基础,分析其原因可能是供给侧结构性改革的实施时间尚短,时间跨度不足以实证分析供给侧结构性改革的长期经济增长效应,有鉴于此,本文在总结前人研究成果的基础上,结合供给侧结构性改革内涵,运用改进索洛模型理论推演供给侧结构性改革的经济增长效应,并通过构建包括家庭、厂商和中央银行等行为主体的DSGE模型,实证模拟供给侧结构性改革的经济增长效应,进一步运用面板平滑转移模型(PSTR模型)对供给侧结构性改革的经济增长效应进行实证检验。

二、供给侧结构性改革经济增长效应理论推演与模拟

(一)全要素生产率视角下供给侧结构性改革经济增长效应理论推演

索洛模型主要用来说明储蓄、资本存量和经济增长之间的相关关系,模型的基本假设前提为:(1)生产函数满足规模报酬不变,要素边际报酬递减,劳动和资本是经济中仅有的相互替代的两种生产要素,技术虽然在模型中有所体现,但它不作为投入要素进入生产函数对产量产生影响,劳动增长率为n,技术增长率为g;(2)f(0)=0,f′(k)>0,f″(k)<0;(3)生产函数满足稻田条件。在具有技术进步的索洛模型中,生产函数具体公式为:

Y(t)=F[K(t),A(t)L(t)]

(1)

式(1)中,Y(t)表示总产出,K(t)表示资本投入,A(t)表示技术投入,L(t)表示劳动投入,A(t)L(t)表示有效劳动投入。结合供给侧结构性改革*供给侧结构性改革涉及劳动力、土地、资本、制度创造、创新等要素,索洛模型包含劳动、资本,技术被看作是非体现的,而技术通过影响资本和劳动要素影响产出,技术应该被看作是体现的,创新多数指技术上的创新,同时,随着城市化进程的加快,土地在经济中扮演的角色越来越重要,一国的制度创造会对产出产生影响,但它并非生产要素,通常以间接的方式作用于经济增长。并参照内托(Neto)等[13-14]关于索洛模型扩展的研究,本文构建如下包含资本、劳动、土地等要素的改进索洛模型:

Y=F[K,BN,DL]

(2)

式(2)中,B表示劳动有效性,N表示劳动投入,BN表示有效劳动投入,D表示土地有效性,L表示土地投入,DL表示有效土地投入。为了检验供给侧结构性改革的经济增长效应,对式(2)求导并整理得:

g=aKgK+aBgB+aNgN+aDgD+aLgL

(3)

其中,aK=K∂Y/Y∂K表示产出资本弹性,aB=B∂Y/Y∂B表示产出劳动有效性弹性,aN=N∂Y/Y∂N表示产出劳动弹性,aD=D∂Y/Y∂D表示产出的土地有效性弹性,aL=L∂Y/Y∂L表示产出土地弹性,由于aK+aB+aN+aD+aL=1,且0≤aj≤1,j=K,B,N,D,L,由式(3)可知,经济稳态增长时,产出增长率与资本增长率、技术增长率、劳动增长率等成正向关系,理论验证了供给侧结构性改革具有一定经济增长效应,技术创新、资本积累、劳动生产率提高和土地利用效率提升等举措能促进我国经济增长。

(二)全要素生产率视角下供给侧结构性改革经济增长效应模拟分析

参考杰森(Giesen)等[15-16]的研究,本文构建符合我国经济实际经济状况的包括家庭、最终厂商、中间厂商和中央银行等行为主体的DSGE模型,实证模拟供给侧结构性改革的经济增长效应。

1.模型构建

(1)家庭。假设经济中存在连续的家庭,满足无限存活、同质特征,家庭效用受消费、实际货币持有量与劳动供给量影响。同时,考虑我国居民具有较强的消费惯性,家庭效用函数中消费项应包含习惯消费;我国居民的劳动供给弹性较低,家庭效用函数劳动供给项应设定为线性形式,代表性家庭的跨期效用函数为:

(4)

Ct+Bt/PtRt+Mt/Pt≤(Mt-1+Bt-1+WtLt+

Dt+Tt)/Pt

(5)

式(5)中,Bt表示家庭持有的名义债券期末余额,Rt表示名义债券利率,Wt表示名义工资,Dt表示家庭获得的利润,Tt表示家庭获得的转移支付。代表性家庭在式(5)约束下最大化其效用现值,得到一阶条件:

λt=ut/(Ct-hCt-1)-βhEt[ut+1/(Ct+1-hCt)]

(6)

ut=λtWt/Pt

(7)

λt=βRtEt[Ptλt+1/Pt+1]

(8)

Mt/Pt=utRt/λt(Rt-1)

(9)

式(6)为家庭关于Ct的一阶条件,λt表示消费的边际效用,式(6)表明一单位正向的偏好冲击会增加家庭消费的边际效用;式(7)为家庭关于Lt的一阶条件,较低的劳动供给弹性决定劳动的稳定的边际效用,式(7)不含Lt;式(8)为家庭关于Bt的一阶条件,家庭放弃一单位当期消费引起的效用损失在数值上等于放弃那一单位消费的货币价值用来购买债券并进行下期消费带来的效用贴现值;式(9)为家庭关于Mt/Pt的一阶条件,表示代表性家庭的实际货币余额需求,名义债券利率越高,家庭愿意持有更多的债券资产,家庭的实际货币余额持有意愿降低。

(2)最终产品厂商。最终产品厂商利用中间产品生产最终产品,对中间产品Yt(i)进行加总得最终产品厂商的生产函数:

(10)

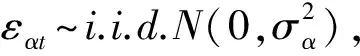
(11)

式(11)中,Pt(i)表示中间产品价格,由式(10)与(11)得中间产品Yt(i)需求函数:

(12)

由于最终产品厂商面临的是完全竞争市场,由零利润原则可得Pt的表达式:

(13)

(3)中间产品厂商。假定中间产品的市场结构为垄断竞争,中间产品厂商生产异质性产品,中间产品厂商的生产函数:

Yt(i)=ZtLt(i)

(14)

(15)

式(15)中,Dt(i)/Pt表示中间产品厂商i分配给家庭的实际利润,水平加总可得Dt,中间产品厂商i面临的约束条件:

(16)

式(16)中,π表示稳态通货膨胀率,[Pt(i)/Pt]-αtWtYt/ZtPt表示实际劳动成本,Wt/Zt表示边际成本,(φ/2)[Pt(i)/πPt-1(i)-1]2Yt表示厂商调整成本,φ表示价格粘性,由式(15)与式(16)得中间产品厂商的一阶条件:

(17)

由式(17)可知,当φ=0时,Pt(i)=Wαt/Zt(αt-1),即中间产品价格为考虑价格加成的边际成本。

(4)产出缺口。本文参考埃尔兰(Ireland)[17]的研究,定义产出缺口xt=Yt/Qt,社会计划者通过选择潜在产出以及分配家庭劳动最大化其社会福利,社会计划者的社会福利函数:

(18)

式(18)中,Qt表示潜在产出,由式(10)与式(14)得社会计划者的约束条件:

(19)

根据式(18)(19)可得社会计划者的一阶条件:

ηt=ut/(Qt-hQt-1)-βhEt[ut+1/(Qt+1-hQt)]

(20)

ut=ηtZt

(21)

根据式(20)与式(21)可以得到潜在产出社会计划者的福利最大化一阶条件:

1/Zt=1/(Qt-hQt-1)-βhEt[ut+1/ut(Qt-

hQt-1)]

(22)

(5)中央银行。中央银行根据“泰勒规则”执行货币政策,名义利率对通货膨胀率与稳态通货膨胀的偏离、产出增长率与稳态产出增长率的偏离做出反应,具体反应系数分别为ρπ和ρg,货币政策的反应系数影响政策冲击持续时间,泰勒规则的具体表达形式:

ln(rt/r)=ρrln(rt-1/r)+ρπln(πt/π)+

ρgln(gt/g)+εrt

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

2.数据选取与参数校准

本文研究区间为1992第1季度至2017第3季度,选取市场利率、通货膨胀率和产出增长率为观测变量,并利用银行间同业拆借利率衡量市场利率(1996年以前数据参考上海融资中心同业拆借利率)、居民消费价格指数(CPI)数据衡量通货膨胀率、国民生产总值(GDP)增长率衡量产出增长率,市场利率、CPI和GDP数据来源于中经网统计数据库和Wind数据库,所有变量数据使用前均经过Tramo-Seats季节调整、HP滤波去趋势,并且通过平稳性检验。

在进行数据分析之前,需要对模型中的参数进行估计或校准,将贴现因子β校准为0.99(β=1/(1+r));参考仝冰[18]的研究将价格调整成本参数φ校准为0.19;参考刘金全等[19]的研究将消费惯性参数h校准为0.7;利用1992—2017年季度通货膨胀率、利率、产出增长率数据校准通货膨胀率稳态值为0.013、利率稳态值0.032、产出增长率稳态值0.024;针对偏好冲击系数ρu、偏好冲击系数标准差σu、全要素生产率冲击标准差σz、价格加成冲击系数ρα、价格加成冲击系数标准差σα、利率平滑系数ρr、货币政策冲击标准差σr、通货膨胀反应系数ρπ、产出缺口反应系数ρx、产出增长率反应系数ρg,鉴于贝叶斯估计相对于普通最小二乘法(OLS)和高斯混合模型(GMM)估计是基于先验分布特征对参数进行事后估计和修正,一定程度上使参数估计更加有效,本文参考巴勃罗(Pablo)等[20]的研究,通过Matlab2017a对模型参数进行贝叶斯估计,通过参数先验分布和卡尔曼滤波估计的似然函数获取参数后验分布后,进一步使用Metropolis-Hastings算法得到整个后验分布,具体估计与校准结果如表1所示。

表1 模型参数校准

3.脉冲响应分析

鉴于本文的研究需要,本文重点观测:(1)全要素生产率冲击、价格加成冲击、偏好冲击和货币政策冲击对产出增长率的动态影响;(2)全要素生产率冲击对产出增长率、通货膨胀率、利率、产出缺口的动态影响。相关冲击及脉冲响应函数如图1所示,其中,横轴表示冲击滞后期,纵轴表示被冲击变量。(a)—(d)显示了1单位的各个冲击对产出增长率的动态影响,(A)—(D)显示了1单位全要素生产率冲击对产出增长率、通货膨胀率、利率、产出缺口的动态影响。

由图1(a)—(d)可知:(1)正向的全要素生产率冲击会提高产出增长率,表现为“陡升缓降”的“正向”冲击特征,产出增长率在第6个季度冲击影响衰减为零*DSGE模型分析的是研究区间内被冲击变量对冲击变量的脉冲响应,文中“产出增长率在第6个季度冲击影响衰减为零”是指一次性全要素生产率冲击发生后,对产出增长率的冲击效应在冲击发生后的第6个季度衰减为零,这不同于时变参数因子增强向量自回归模型(SV-TVP-FAVAR模型)的时点脉冲冲击,下文不再解释。,全要素生产率的提升带来要素使用效率的提升,进而带来产业增长率的上升;(2)正向的价格加成冲击使产出增长率出现正负交替,表现为“陡升陡降”的“正向→负向”冲击特征,短期内由于存在信息不对称,正向的价格加成冲会使中间厂商获利增多,加大中间产品的生产,进而带来产出增长率的上升,随后的信息公开会带来中间产品厂商的低效率生产,进而带来产出增长率的迅速下降,产出增长率在第2个季度使产出增长率迅速下降至负值,并在第10个季度冲击影响衰减为零;(3)正向的偏好冲击短期内会使产出增长率出现负正交替,表现出“陡降陡升”的“负向→正向”冲击特征,正向的偏好冲击会使消费者极短时间内找不到合适的产品进行消费,带来产出增长率的下降,但在中长期内,正向偏好冲击会使家庭当期消费边际效用提高,且家庭会对下期可能发生的冲击有一定预期,家庭增加当期的消费有益于提高家庭效用,进而带来产出增长率的上升,产出增长率在第2个季度使产出增长率迅速上升至正值,并在第5个季度冲击影响衰减为零;(4)正向的货币政策冲击会降低产出增长率,表现出“陡降陡升”的“负向→零”冲击特征,正向的货币政策冲击会使利率水平上升,激励家庭减少当期消费,增加未来消费,进而带来产出增长率的下降,但长期内货币政策冲击对产出增长率的影响效果不明显,产出增长率在第2个季度使产出增长率迅速上升至零。

(a)全要素生产率冲击 (b)价格加成冲击 (c)偏好冲击 (d)货币政策冲击

(A)产出增长率 (B)通货膨胀率 (C)利率 (D)产出缺口图1 相应冲击与脉冲反应函数

由图1(A)—(D)可知:(1)正向的全要素生产率冲击会提高使产出增长率,影响周期相对较长;(2)正向的全要素生产率冲击可以降低通货膨胀率,正向的全要素生产率冲击通过提高产品生产效率提高了中间产品厂商的生产能力和最终产品的供给能力,进而带来物价水平的下降,达到降低通货膨胀率的目的;(3)正向的全要素生产率冲击会降低市场利率,正向的全要素生产率冲击通过降低产品的生产成本降低市场货币需求,进而带来银行间同业拆借利率的下降;(4)正向的全要素生产率冲击能够减小产出缺口,通过增加经济社会的产出水平,缩小实际产出水平与潜在产出水平的偏离。

通过比较全要素生产率冲击、价格加成冲击、偏好冲击、货币政策冲击对产出增长率的动态影响及其影响周期与全要素生产率冲击对产出增长率、通货膨胀率、利率、产出缺口的动态影响及其影响周期可知,全要素生产率冲击更利于提高产出增长率,且全要素生产率在提高产出增长率的同时,带来了“低通胀、低利率、低产出缺口”的溢出效应,并未带来“外部不经济”,因此,基于全要素生产率视角下的供给侧结构性改革成为经济稳态运行的“帕累托最优”,提高全要素生产率有利于我国经济健康、持续发展。

三、供给侧结构性改革经济增长效应实证检验

为了进一步验证供给侧结构性改革的经济增长效应,本文基于全要素生产率视角,运用面板平滑转移模型(PSTR模型)实证检验供给侧结构性改革的经济增长效用。

(一)全要素生产率视角下的最优储蓄率

新常态下,消费作为拉动经济增长的主要动力,正向驱动作用明显,在经济增长动力转换过程中发挥着不可替代的作用,由新古典经济增长理论下储蓄率的传导渠道可知,储蓄率通过影响有效人均消费影响实体经济,储蓄率成为治理消费需求不足、促进经济增长的有效途径,由式(1)可得公式:

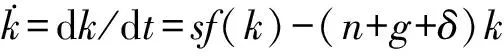
(34)

sf(k)=(n+g+δ)k

(35)

由式(35)可知,不同储蓄率对应不同的稳态均衡点,提高储蓄率会带来经济增速短暂上升和经济永久性增长,同时,有效人均消费经过瞬时下降后迅速上升,直到达到新的稳态消费,为了分析储蓄率变动后有效人均消费的变化情况,构建公式:

c=(1-s)f(k)=f(k)-(n+g+δ)k

(36)

式(36)中,c表示有效人均消费,将式(36)进一步微分得公式:

dc/ds={f′[k(s,n,g,δ)]-

(n+g+δ)}∂k(s,n,g,δ)/∂s

(37)

当经济达到稳态时,∂k*(s,n,g,δ)/∂s>0,由式(37)可知,储蓄率与有效人均消费之间的关系取决于f′[k*(s,n,g,δ)]-(n+g+δ)的正负。具体来说:当f′[k*(s,n,g,δ)]-(n+g+δ)<0时,提高储蓄率,有效人均消费减小;当f′[k*(s,n,g,δ)]-(n+g+δ)>0时,提高储蓄率,有效人均消费增加。

针对“储蓄率→有效人均消费→实体经济”传导渠道,以提高储蓄率为例,上述传导渠道具体为:

传导渠道a:“提高储蓄率→有效人均消费减小→经济增长”;

传导渠道b:“提高储蓄率→有效人均消费增加→经济增长”。

传导渠道a和传导渠道b为新古典经济增长理论下储蓄率的传导渠道,即提高储蓄率会带来经济增长,考虑到我国经济可能存在不满足新古典经济增长理论的情形,现实经济可能存在另外两个传导渠道:

传导渠道c:“提高储蓄率→有效人均消费减小→经济衰退”;

传导渠道d:“提高储蓄率→有效人均消费增加→经济衰退”。

在a、b、c、d四种传导渠道下,储蓄率的提高对实体经济的影响是不同的,具体影响取决于f′[k*(s,n,g,δ)]-(n+g+δ)的正负,而f′[k*(s,n,g,δ)]-(n+g+δ)的正负由n、g和δ的数值决定,全要素生产率参数通过影响储蓄率传导渠道进而影响实体经济,储蓄率处于什么水平更利于经济增长?该状态下的储蓄率要求全要素生产率参数满足什么条件?为了解决上述问题,本文进一步将式(2)具体化为:

Y=F[K,VEN,HWL]

(38)

式(38)中,V表示技术分配促进劳动的体现技术进步,E表示技术分配促进劳动的非体现技术进步,H表示技术分配促进土地的体现技术进步,W表示技术分配促进土地的非体现技术进步,由式(38)得公式:

(gl+gh+ξ+ζ+δ2)k

(39)

式(39)中,f1(k)表示有效人均资本产出,gv表示技术分配促进劳动的体现技术进步增长率,ω和ψ分别表示技术分配促进劳动的非体现技术进步增加的资本增长率和劳动增长率,δ1表示劳动资本折旧率,f2(k)表示有效地均资本产出,gl表示土地增长率,gh表示技术分配促进土地的体现技术进步增长率,ξ和ζ分别表示技术分配促进土地的非体现技术进步增加的资本增长率和土地增长率,δ2表示土地资本折旧率,整理式(39)得公式:

(40)

式(40)中,f(k)表示有效资本产出(f(k)=f1(k)+f2(k)),gb表示劳动有效性增长率(gb=n+gv+ω+ψ),gd表示土地有效性增长率(gd=gl+gh+ξ+ζ),δ表示资本折旧率(δ=δ1+δ2)。经济稳态增长时,最优储蓄率的核算公式:

(41)

式(41)中,s*表示最优储蓄率(本文指供给侧结构性改革下以经济稳态增长为目标的应有储蓄率),g表示产出增长率(g=gb+gd)。运用式(41)可以测算最优储蓄率,其中,资本折旧率参考胡永刚等[21]的δ值(0.1)和范祚军等[22]的δ值(0.05),取两者平均值δ=0.075;资本存量通过公式Kt=It+Kt-1(1-δ)核算;产出增长率g′=(GDPt-GDPt-1)/GDPt-1。经《中国统计年鉴》查询相关数据计算1979—2015年我国最优储蓄率,并与实际储蓄率进行比较,具体情况如图2所示。从中可见,1979—2015年我国实际储蓄率与最优储蓄率走势基本一致,但实际储蓄率长期高于最优储蓄率,我国经济可能存在“高储蓄率之谜”,1979—2015年我国实际储蓄率的峰值、均值和谷值分别为57.96%、40.41%和25.31%,最优储蓄率的峰值、均值和谷值分别为34.20%、29.62%和24.05%。“十二五”以来,我国平均储蓄率维持在45%—55%,最优储蓄率维持在25%—35%,我国实际储蓄率明显偏高。2010年以后,经济增长方式由依靠投资、出口拉动向依靠消费、投资、出口协同拉动的转变使我国实际储蓄率与最优储蓄率呈现趋势性下降。

图2 实际储蓄率与最优储蓄率

图3 储蓄率缺口与产出增长率缺口

(二)最优储蓄率视角下的供给侧结构性改革

为确定全要素生产率视角下的最优储蓄率相较于实际储蓄率是否更利于经济增长,本文运用PSTR模型对我国实际储蓄率与产出增长率之间的关系进行分析。

1.变量选取与数据来源

为了研究实际储蓄率与经济增长之间的关系,本文选取我国31个省份2001—2015年的产出增长率作为被解释变量、实际储蓄率作为解释变量、资本形成率与通货膨胀率作为控制变量、实际储蓄率作为模型中的门限变量。研究所用数据主要来源于《中国统计年鉴》《新中国60年统计资料汇编》及各省统计年鉴。需要说明的是实际储蓄率的核算问题,一般来说,计算储蓄率有支出法与生产法两种方法:一是支出法,通过“储蓄率=1-最终消费率”近似核算;二是生产法,通过资金流量表核算。两种方法各有利弊,针对本文样本的省级数据特征及时间跨度选取,上述两种核算储蓄率的方法均难以实现,为此本文结合各省共性特征与个体特征采用转换法核算省级实际储蓄率。具体来说,可以通过式(41)计算出各省2001—2015年最优储蓄率,进一步转换成各省2001—2015年实际储蓄率,最优储蓄率向实际储蓄率转换的关系式设定为:

(42)

2.模型构建与检验

鉴于经济状态并非跳跃式转换,传统PTR模型的突变特征不合理,为了克服PTR模型存在的转换机制跳跃、离散的问题,使模型转换变量连续平滑转换,且能有效获取数据截面异质性,本文构建PSTR模型如下:

(43)

为避免变量数据出现虚假回归,本文采用LLC检验方法对变量数据进行平稳性检验,平稳性检验结果显示,模型分析的被解释变量、解释变量、门限变量、控制变量数据均在1%的置信水平上拒绝存在单位根的原假设,各个变量数据均表现出良好的平稳性,可以构建面板回归模型。

在使用模型前,需对实际储蓄率与产出增长率之间的非线性关系、转换函数个数和最佳m值进行检验,具体结果如表2所示。(1)模型的非线性检验原假设H0:γ=0(系统只存在一个机制);备择假设H1:γ=1(系统存在两个机制)。检验结果显示:无论m=1或m=2,LM、LMF和LRT统计量均1%的显著性水平上拒绝原假设,可以使用PSTR模型分析我国实际储蓄率与经济增长之间的非线性关系。(2)模型转换函数个数检验的原假设H0:r=1(存在一个非线性转换函数);备择假设H1:r=2(存在两个以上非线性转换函数)。检验结果显示:无论m=1或m=2,均不能拒绝原假设,确定模型只含有一个非线性转换函数。此外,本文采用AIC和BIC准则确定最佳位置参数个数,检验结果显示:m=1的两个转换变量所对应的AIC值(-5.741)和BIC值(-5.670)均小于m=2时的AIC值(-5.735)和BIC值(-5.654),确定模型的位置参数个数m=2。

3.参数估计与结果分析

鉴于PSTR模型的非线性特征,OLS估计不再适用,本文运用非线性最小二乘法(NLS)来对模型参数进行估计,具体变量系数在低区制和高区制下的估计值与t值如表3所示。

表2 模型非线性与转换函数个数检验结果

注:括号内数值为P值,***表示在1%的显著性水平上显著。

表3 参数估计结果

注:***、**和*表示在1%、5%和10%的显著性水平上显著。

图4 平滑转移函数

4.供给侧结构性改革经济增长效应检验

供给侧结构性改革就是从提高供给质量出发,矫正要素配置扭曲,扩大有效供给,提高全要素生产率,供给侧结构性改革涉及劳动力、土地、资本、制度创造、创新等要素。通过我国实际储蓄率与产出增长率相关数据,画出我国实际储蓄率与产出增长率关系图,如图5所示。结合PSTR模型门限值与图5可知,在储蓄率门限值两侧,随着储蓄率的持续降低,我国产出增长率逐步上升。具体来说,在储蓄率高区制下,储蓄率的降低带来产出增长率的缓慢增长;在储蓄率低区制下,储蓄率的降低带来产出增长率的显著增长;储蓄率门限值两侧,储蓄率对产出增长率的影响程度不同,储蓄率由高区制向低区制过渡带来产出增长率的“缓增”向“陡增”过渡,储蓄率门限值为实际储蓄率与产出增长率关系曲线凹凸“拐点”。可以通过以下两个因素理解低区制、高区制下降低储蓄率的经济增长效果:(1)不同区制下拉动产出增长率的主要因素不同;(2)挤出货币的消费投资比不同。以储蓄率高区制为例,假设t时期,维持原有产出增长率的消费投资比为a且拉动产出增长率的主要因素是消费,降低储蓄率会向市场挤出新的货币供给,如果挤出的货币供给在消费和储蓄的分配比例小于a,降低储蓄率就会带来产出增长率的缓慢上升,反之产出增长率会显著上升。

图5 实际储蓄率与产出增长率关系

具体来看,2002—2015年我国实际储蓄率和最优储蓄率均值分别为48.24%和31.44%,储蓄率门限值(35.94%)位于实际储蓄率与最优储蓄率之间,我国实际储蓄率向储蓄率门限值趋近过程中,产出增长率缓慢增长,进一步向最优储蓄率趋近过程中,产出增长率显著增长,适当降低我国储蓄率将成为一个利于经济增长的帕累托改进。但并不是说可以通过持续降低储蓄率的方式来提高产出增长率,除了受国家经济体制、居民消费习惯等因素影响外,家庭、企业和政府的预期交易动机、预期谨慎动机和当期消费动机等因素致使储蓄率存在“储蓄率下限”和“储蓄率上限”,实际储蓄率的下限和上限决定了实际储蓄率与产出增长率关系曲线只存在一个“拐点”(单门限值)而不是存在多个“拐点”(多门限值)。

总结来看,基于全要素生产率视角下的最优储蓄率小于基于PSTR模型分析得出的我国储蓄率门限值,说明我国实际储蓄率向储蓄率门限值进而向最优储蓄率趋近会拉动经济增长,实证检验出供给侧结构性改革具有一定经济增长效应,“十九大”报告中也再次重申我国需要继续深化供给侧结构性改革。

四、结论与讨论

新常态下,我国经济站在新起点的最大特征就是要用新理念和新实践去应对新变化带来的新挑战。本文立足微观视角分析宏观问题,基于全要素生产率视角对供给侧结构性改革的经济增长效应进行理论推演、实证模拟与检验,得出以下主要结论:第一,基于全要素生产率视角下改进索洛模型理论推演显示,提高资本增长率、技术增长率等可以带来经济增长,供给侧结构性改革具有一定经济增长效应,符合政府提出的“供给侧改革”的核心。第二,基于全要素生产率冲击视角的动态随机一般均衡模型模拟分析显示,相较于价格加成冲击、偏好冲击、货币政策冲击,全要素生产率冲击更利于提高产出增长率,且带来了“低通胀、低利率、低产出缺口”的溢出效应,基于全要素生产率视角下的供给侧结构性改革成为经济稳态运行的“帕累托最优”,提高全要素生产率有利于我国经济健康持续发展。第三,基于全要素生产率视角下的面板平滑转移模型实证检验显示,我国最优储蓄率小于储蓄率门限值,实际储蓄率向储蓄率门限值进而向最优储蓄率趋近会带动经济增长,供给侧结构性改革具有一定经济增长效应,新常态下,“三期叠加”阵痛效应成为我国经济最大的特征和挑战,以供给侧结构性改革为主线、推动经济发展质量变革、效率变革、动力变革对于我国经济健康良性发展至关重要。

此外,需要说明的是:(1)封闭的DSGE模型问题。本文通过封闭的DSGE模型模拟分析供给侧结构性改革经济增长效应,并未构建开放的、多行为主体的DSGE模型分析更多冲击对经济增长的影响,主要原因在于本文旨在分析全要素生产率冲击对经济增长的影响,进而分析供给侧结构性改革的经济增长效应,模型复杂与否并不会对分析结果产生本质影响;(2)模糊比较与精准分析问题。本文在分析全要素生产率冲击、价格加成冲击、偏好冲击、货币政策冲击对产出增长率的动态影响与全要素生产率冲击对产出增长率、通货膨胀率、利率、产出缺口的动态影响时,只对其影响趋势进行对比分析,并未对具体效果进行精确数值分析,主要原因在于通过简单的趋势与幅度对比分析便可得出不同冲击对产出增长的影响优劣,达到对比分析的目的;(3)新常态下最优储蓄率确定问题。本文通过分析实际储蓄率、储蓄率门限值与最优储蓄率三者之间的大小关系,得出实际储蓄率向储蓄率门限值和最优储蓄率的逐步趋近会带来经济增长,但考虑到制度因素、消费习惯、预防性储蓄等,我国实际储蓄率下降多少可以实现“多因素”下的“帕累托最优”问题尚未给出答案,主要原因在于本文旨在证明全要素生产率视角下的最优储蓄率更利于经济增长,进而检验供给侧结构性改革具有一定经济增长效应,最优储蓄率作为一个基准概念,本身就是经济稳态增长时的应有储蓄率,只起基准指标的作用。

总之,新常态时期,我国经济面临下行风险,深入贯彻供给侧结构性改革,全面加快技术创新、提高劳动生产率、土地利用率等可以带来我国经济持续稳定增长,供给侧结构性改革具有一定经济增长效应。

[参考文献]

[1] 汪红驹, 汪川. 国际经济周期错配、供给侧改革与中国经济中高速增长[J]. 财贸经济, 2016(2): 5-19.

[2] 贾康, 苏京春. 论供给侧改革[J]. 管理世界, 2016(3): 1-24.

[3] 洪银兴. 准确认识供给侧结构性改革的目标和任务[J]. 中国工业经济, 2016(6): 14-21.

[4] 刘伟. 经济新常态与供给侧结构性改革[J]. 管理世界, 2016(7): 1-9.

[5] 金碚. 基于价值论与供求论范式的供给侧结构性改革研析[J]. 中国工业经济, 2017(4): 5-16.

[6] 冯俏彬, 贾康. 我国供给侧改革的背景、理论模型与实施路径[J]. 经济学动态, 2017(7): 35-43.

[7] 方福前. 寻找供给侧结构性改革的理论源头[J]. 中国社会科学, 2017(7): 49-69+205.

[8] 徐朝阳. 供给抑制政策下的中国经济[J]. 经济研究, 2014(7): 81-93+124.

[9] 王海军, 冯乾. 供给侧结构性改革的经济学理论内涵——基于总供给总需求的分析框架[J]. 西安交通大学学报(社会科学版), 2016(6): 9-15.

[10] 余泳泽. 异质性视角下中国省际全要素生产率再估算: 1978—2012[J]. 经济学(季刊), 2017(3): 1051-1072.

[11] 马彪, 林琳, 吴俊锋. 供给侧结构性改革中产能、金融支持与经济波动关系研究[J]. 产业经济研究, 2017(5): 12-24.

[12] 徐晋. 新解构发展经济学——价值空间、测度体系与供给侧改革结构方程[J]. 西安交通大学学报(社会科学版), 2018(1): 1-14.

[13] NETO J P J, CLAEYSSEN J C R. Capital-induced labor migration in a spatial Solow model[J]. Journal of Economics, 2015(1): 25-47.

[14] PARK J S, SEO Y J. The impact of seaports on the regional economies in South Korea: Panel evidence from the augmented Solow model[J]. Transportation Research Part E, 2016(85): 107-119.

[15] GIESEN S, SCHEUFELE R. Impulse response analysis in a misspecified DSGE model: a comparison of full and limited information techniques[J]. Applied Economics Letters, 2016(3): 162-166.

[16] 郑挺国, 黄佳祥. 中国宏观经济下行区间的冲击来源及其差异性分析[J]. 世界经济, 2016(9): 28-52.

[17] IRELAND P N. Technology Shocks in the New Keynesian Model[J]. The Review of Economics and Statistics, 2004(4): 923-936.

[18] 仝冰. 混频数据、投资冲击与中国宏观经济波动[J]. 经济研究, 2017(6): 60-76.

[19] 刘金全, 徐宁, 刘达禹. 资产价格错位与货币政策规则——基于修正Q理论的重新审视[J]. 国际金融研究, 2017(5): 25-35.

[20] PABLO G Q, ATSUSHI I, LUTZ K. Impulse response matching estimators for DSGE models[J]. Journal of Econometrics, 2017(1): 144-155.

[21] 胡永刚, 郭长林. 财政政策规则、预期与居民消费——基于经济波动的视角[J]. 经济研究, 2013(3): 96-107.

[22] 范祚军, 常雅丽, 黄立群. 国际视野下最优储蓄率及其影响因素测度——基于索洛经济增长模型的研究[J]. 经济研究, 2014(9): 20-33.