提高RTK测量计算精度的方法

（淮河工程集团有限公司 徐州 221009）

随着科学技术的不断创新，施工测量设备也在不断更迭，在大土方量工程和水下土方测量上RTK设备的应用越来越广泛。本文结合淮河某工程施工中RTK设备测量数据，以河道开挖工程测量为例，阐述RTK设备在工程测量中遇到的相关问题及解决问题的方法。

1 RTK设备在工程测量中遇到的问题

河道开挖工程中，设计文件给出了河道断面基点以及设计中心线坐标。断面测量即通过RTK设备在以此两点形成的直线上采集数据，并得到测点的坐标与高程，通过两点间的距离和测点高程进行作图计算。但在实际测量中采集到的部分测点与设计断面线略有偏差:如图1所示基点与中心点所在的直线为设计断面线，n0～nx为实测点，其中部分测点偏离测线。

主要原因有:（1）RTK设备的局限性。当RTK设备上方存在树木等遮挡物时，会影响其信号的接收，不能得到准确的数据。在实际采点时遇到这种情况，只能偏离测点或者设计测线以外寻求信号，保证测点的完整性；（2）设计断面线上的随机测点不具备特征点的性质时不能采用。现场测量时测量员会偏移测点，在其附近寻找合适测点代替原测点，以达到测量数据的合理性；（3）测量人员的业务能力和对设备的操作熟练程度也会影响测量点的选取。

2 通过修正计算消除影响

该方法利用海伦公式计算、处理数据，将偏离的测点投影到设计断面上，通过修正计算得到精确结果。如图2所示n0～nx通过计算修正后得到他们在设计断面线上的投影点o0～ox。

海伦公式是利用三角形的三条边的边长（a、b、c）直接求三角形面积的公式。假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得而公式里的p为半周长:

具体计算过程为:基点坐标为（X基，Y基）、中心点坐标为（X中，Y中）、实测点 n4点坐标为（X4，Y4）（如图 3 所示）。

距离基点距离

图1 设计断面线图

图2 修正后设计断面线图

图3 计算断面线图

表1 采集数据处理表

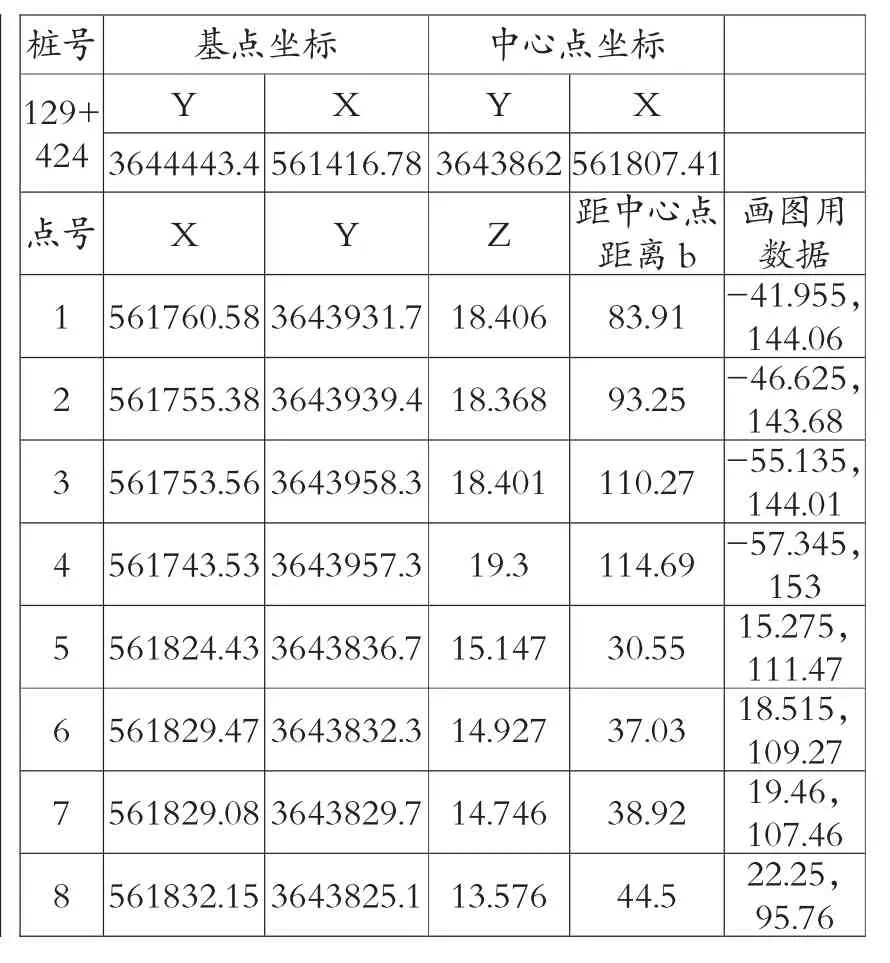
表2 采集数据处理表

图4 修正后计算数据作图

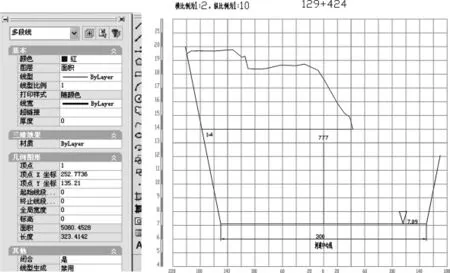
图5 传统数据作图

距离中心点距离

中心点与基点距离:

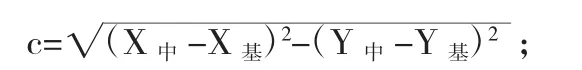
p 为三边和除以 2，既

S 为面积

通过面积求出偏移距离:d=S/c×2，距中心点距离为

l的数值即为n4点在直线上的投影o4点。

o4点即为修正点，最后通过距离和已知高程Z点作图求出面积，计算数据见采集数据处理表1。

采集数据处理表中点号、X、Y、Z为采集的数据，通过上述公式计算得出修正后距离，通过距离和高程的数据作图，并用CAD作图计算，即图4中14.0m高程以上的129+424断面面积为5081.25m2。

3 与传统计算方法的比较

传统的计算方法为采集数据处理表2，通过点号数据与中心点坐标数据计算两点间距离，得出距中心点距离，通过数据在图中的比例尺得出画图用数据栏。通过CAD作图计算，得出图5中129+424断面14m高程以上的面积为5080.45m2。

原数据图上面积为5080.45m2，实际面积为1016.09m2，经过修正计算得到的数据图上面积5081.25m2，实际面积为1016.25m2。通过比较，该计算方法提高了计算精度。

受篇幅限制，此次计算仅列举测点8个。虽然得到修正后的结果看似悬殊不大，但对该工程成千上万个测量点及几千万土方来说影响较大。

4 实际应用结论

（1）该计算方法不仅对陆上测量数据有较好的校正作用，对水下测量数据的校正作用更为明显，因为测量船体摆动幅度比较大，测点偏离设计线的可能性更高。

（2）计算过程中的偏移距离可以复核测量工作的质量，并能精确地找出问题测点，进而复测或修正。

（3）对于无设计资料或者不规则的区域测量，可先进行采点工作，然后在平面图上假设一条设计断面线，把测点校正到此线上进行运算，进而得出相对精确的结果■