探究一道与三角形有关的高考题

□王 娟

2018年高考江苏卷第13 题是一道与三角形有关的最值题.

例1在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为________.

解法1：利用面积拆分相等.

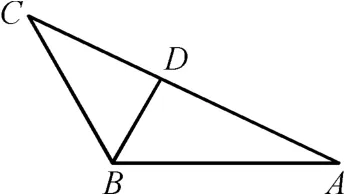
图1

因为S△ABC=S△ABD+S△BCD，

化简得：ac=a+c.

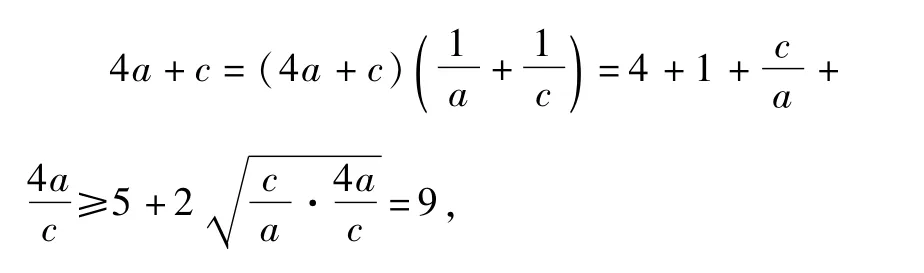
当且仅当c=2a 时等号成立.

解法分析：由于已知夹角的大小，所以直接从面积公式出发，利用面积相等，从而得到边之间的关系式.

解法2：解析几何法.

以点B为坐标原点，BA所在直线为x轴，过点B与BA垂直的直线为y轴，建立如图2所示平面直角坐标系.

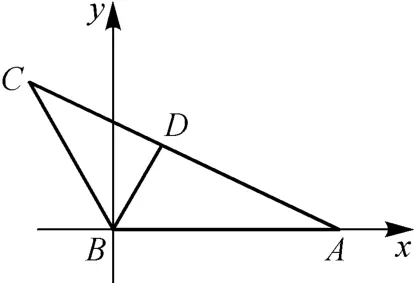
在平面直角坐标系中，B（0，0），A（c，0），

因为A，D，C三点共线，所以kAD=kCD，即

化简得：ac=a+c.

以下同法1.

当然建系有多种建法，我们也可以以点B为坐标原点，BD所在直线为x轴，过点B与BD垂直的直线为y轴，建立如图3所示的平面直角坐标系.

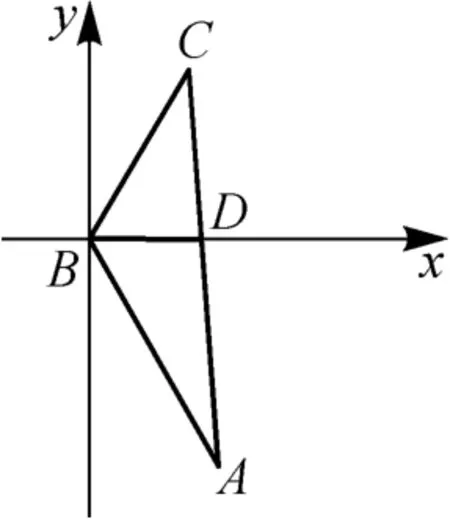
图3

利用三点共线同样可以得到ac=a+c.

本题还有其他解法，这里就不一一详述，主要针对直接运用解三角形的方法和建立直角坐标系的方法来探讨一下关于这类题目的解法.

同样类似的题目有：2011年南通一模第14 题：

例2已知等腰三角形腰上的中线长为则该三角形面积的最大值为________.

解法1：直接利用面积公式.

根据题意画出图形，如图4所示.

图4

设AB=AC=2a，由D是AB的中点，得到AD=DB=a.

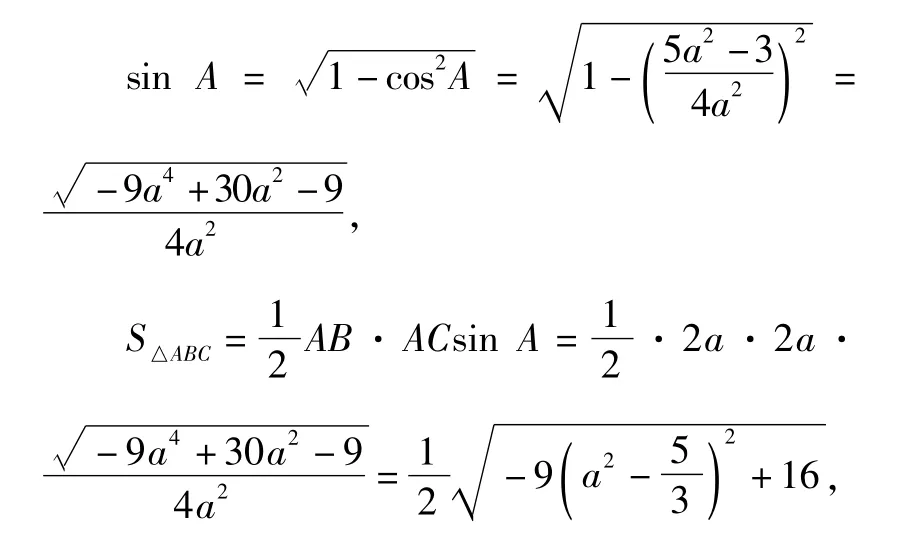
该方法直接从余弦定理出发，结合面积公式，转化为函数问题求最值.

解法2：解析几何法.

以BC中点为坐标原点，BC所在直线为x轴，线段BC的中垂线为y轴，建立如图5所示平面直角坐标系.

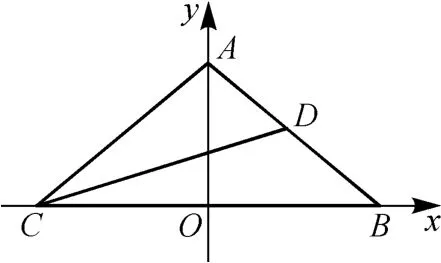
图5

9a2+b2=12，

当且仅当3a=b时，等号成立.

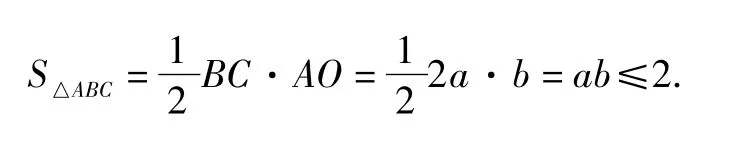
所以当3a=b时，三角形面积最大值为2.

解法探究：由南通联考题到高考题，这样两种思路整体建立在这两个三角形本身有足够特殊的地方，有异曲同工之处.比如例2 是一个等腰三角形，而例1 的三角形中有60°和120°这样的特殊角，所以我们在除了运用最基本的解三角形的思路之外，考虑建立平面直角坐标系，运用解析几何的方法可以更好更快速地解决问题.我们在解三角形的题目时，如果碰到三角形中存在特殊角，适当的时候可以考虑建立平面直角坐标系来解决问题.