膜计算在图像处理领域应用研究综述
2018-05-24袁建英张葛祥郭德全
袁建英,张葛祥,郭德全,蒋 涛
(1. 成都信息工程大学 控制工程学院,四川 成都 610225; 2. 四川汽车关键零部件协同创新中心 博士后创新实践基地,四川 成都 610039; 3.西华大学 机器人研究中心,四川 成都 610039;4.西南交通大学 电气工程学院,四川 成都 610031; 5. 电子科技大学 航空航天学院,四川 成都 610054)
图像作为人类感知世界的视觉基础,是人类获取信息、表达信息和传递信息的重要手段.数字图像处理是信号与信息处理学科的重要组成部分,起源于20世纪20年代,其作为一门学科大约形成于20 世纪 60 年代初期[1].在过去几十年,伴随计算机、集成电路、光学成像、视觉理论等技术的飞速发展,图像处理在算法、系统结构以及应用领域都进入大发展时期,在诸如农业生产、航空航天、通讯交通、医学国防等领域都扮演了重要的角色.然而,伴随高帧率、高分辨率成像器件的成熟应用,图像数据越来越多;与此同时,先进的数学理论不断被引入图像处理领域,图像处理算法越来越复杂.在这种情况下,传统的处理器体系结构在很多情况下已不能提供足够的数据处理能力.海量图像数据、复杂算法与实时性之间的矛盾成为图像处理领域的一大挑战[2].
鉴于传统处理器体系结构对海量图像实时处理存在瓶颈,无论是图像处理理论界还是工程界都迫切需求一种新的计算体系结构.欧洲科学院院士乔治伯恩(George Păun)于1998年在芬兰图尔库计算机中心首次提出膜计算[3](membrane computing),它是自然计算的新分支,旨在模拟生命细胞的结构和功能,创建一种分布式并行计算模型.自膜计算提出后,研究者们已经证明膜计算模型不但具有图灵机一样强大的计算能力,且能有效的解决许多计算困难问题,如NP(non deterministic polynomial)完全问题[7].
在近10年时间里,图像处理对高速并行处理的需求、膜计算天然的并行计算能力得到众多学者的关注.自2011年起,陆续有膜计算在图像处理领域应用的报道,这些研究成果为膜计算的应用研究开辟了一个新的方向,同时也为图像处理领域提供了一种新的研究手段.论文先介绍图像处理和膜计算的基础知识,接着对膜计算在图像低层处理和中层处理领域的研究进行综述,最后展望了膜计算与图像处理相结合的未来研究方向.
1 图像处理简述
早期图像处理以改善人类的视觉效果为目的.从20世纪70年代中期开始,人们开始研究如何用计算机系统理解图像.根据研究方法和抽象程度的不同,图像处理研究内容可分为3个层次[4-5]:低层图像处理、中层图像处理、高层图像处理,分别对应图像处理、图像分析和图像理解,如图1所示.

图1 图像处理3层次
低层图像处理:输入图像,输出也是图像.低层图像处理是图像分析的基础,其目的是改善视觉效果或突出有用信息.常见的低层图像处理算子有:点操作算子(对比度增强)、局部操作算子(图像滤波、边缘检测等)和全局操作算子(图像熵的计算、图像分割阈值计算等).
中层图像处理(图像分析):输入图像,输出数据.在低层处理的基础上,建立图像中感兴趣区域的描述,将以像素描述的图像转变为简洁的符号描述.如图像分割、目标跟踪、立体3维重建等.
高层图像处理(图像理解与表达):输入数据,输出理解.在中层图像处理基础上,进一步研究图像中各目标的性质及相互联系,得出对场景的理解和解释,从而指导和规划行动.如车牌识别、人脸识别、交通信号灯识别等.
需要指出的是,狭义的图像处理指低层操作,主要在像素级上进行处理,因此数据量巨大.经中层特征提取与描述后,把原来以像素构成的图像转变成比较简洁的、非图像形式的描述,数据量减少.图像理解是高层操作,旨在对中层图像抽象出来的符号进行推理,其处理过程和方法与人类的思维推理有许多类似之处[40].
2 膜计算简述
膜计算模型又称为膜系统或P系统,由膜结构、对象多重集和进化规则3要素构成.截至目前,主要有3种类型的膜计算模型:细胞型、组织型和神经型膜系统[6-7].
细胞型膜计算模型模仿细胞的结构和功能,由膜结构、对象和规则组成.膜结构将膜进行分层安排,膜用于划分放置对象多重集的区域.对象通常用字母表中的字符或字符串表示.规则用于处理对象或膜,每条规则明确地指出需要处理的对象或膜以及具体需要执行的操作.细胞型膜系主要包含转移P系统、转运P系统和活性膜P系统.
组织型膜系统将多个细胞自由放置在同一环境中,细胞和环境中均可包含对象、各细胞之间和细胞与环境之间采用转运规则进行通信.典型的组织型膜系统包括:基本组织型P系统、种群P系统和P群.
神经型膜系统中的细胞均采用神经元细胞,是组织型膜系统的拓展模型,主要有两种类型:基本神经型膜系统和脉冲神经型膜系统.
3 膜计算在图像处理中的应用
图像处理包含内容较多,从已有的研究来看,膜计算在图像处理领域的应用主要集中在图像低层和中层处理,膜计算在图像高层处理的应用尚未见报道.
3.1 低层图像处理
3.1.1 图像平滑
传统的诸如均值、中值平滑算法是一种以区域为操作对象的方法,随着图像分辨率增加,传统串行计算时间会急速增加.文献[8]提出了用组织型P系统设计图像平滑算法,设计了度为1的P系统,定义了平滑运算规则:当两个相邻像素灰度差小于设定阈值时,较大灰度值用较小灰度值代替.由于图像上所有相邻像素对可同时执行此规则,因此能在线性时间内完成图像平滑计算.文中分析了平滑算法的计算复杂度,膜系统需要的资源,包括需要字母表的大小、初始细胞数、初始对象数、规则数量,规则长度的上界.文献[9]给出了在CUDA上执行平滑算法的具体步骤,以及计算复杂度分析.图2是文献[8]图像平滑后的结果.
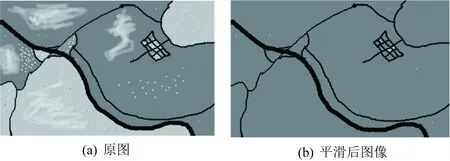
图2 文献[8]图像平滑实验结果
3.1.2 图像骨架提取
图像骨架反映了目标的形状,通过提取图像骨架可以用较小的数据量表示目标形状,有利于目标检测与识别.文献[10]将膜计算、细胞多重集(cell complex)和图像细化算法相结合,设计了一系列有优先次序规则的组织型P系统,实现了文献[11]中的图像细化算法.当输入图像的尺寸是O(nk),系统所需的计算步骤数≤7k(n+1)+3.实验结果如图3所示.

图3 文献[10]图像骨架提取实验结果
3.2 中层图像处理
3.2.1 图像分割
图像分割是将像平面内具有相同或者接近属性(如图像的灰度、颜色、轮廓、纹理等)的区域归类,各区域内像素属性接近,而不同区域像素属性存在较大差异.传统的图像分割算法有基于区域、基于边缘和两者相结合的方法.已有的报道均针对传统分割算法,目前膜计算在较新颖图像分割算法的应用鲜见报道,这些新理论包括:基于模糊理论、神经网络、支持向量机、人工免疫等的分割算法等.分析已有报道可见,膜计算在分割中的应用可分为两大类:一是基于膜计算模型的图像分割方法,该方法主要利用膜计算的并行性,对特定的分割算法设计相应的膜系统,提高图像分割算法执行效率;二是基于膜优化算法的图像分割方法,该方法主要借助膜优化算法强大的优化能力,提高传统分割算法的分割性能.
(1) 基于膜计算模型的图像分割
这方面的研究主要以基于边缘检测的图像分割算法为研究对象,设计相应的膜系统,从理论上分析膜系统图像分割时间复杂度、膜系统所需要的资源.该内容的研究以西班牙塞维利亚大学Díaz等人为主,他们在2011-2014年间共发表了6篇相关论文.现以文献[12]为例说明该类方法的核心思想,其他类似报道见文献[13-17].
在文献[12]中,作者并没有通过传统的差分计算来实现边缘检测,而是直接比较相邻像素大小来检测边缘.假定图像大小为n×m,定义度为2的组织型P系统为
Π1(n,m)=(Γ,Σ,ε,w1,w2,R,iΠ,OΠ),
其中
(a) 系统工作集:Γ=Σ∪ε.
(b) 系统输入集:Σ={aij:a∈C,i∈[1~n],j∈[1~m]}.
(e) 规则R:



图4 规则2所包含的4种位置结构示意图

图5给出了规则3中4条规则对应的4种相邻像素结构,其中:红色表示已被标记为边界的像素,※表示像素a所在的位置,○表示像素b所在的位置.当a的颜色值小于b的颜色值时,将a标记为边界像素.

图5 规则3所包含的4种相邻位置结构示意图
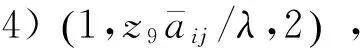
(f) 输入细胞:iΠ=1;输出系统:OΠ=0.
系统执行过程如下:当aij进入细胞1时,首先在细胞1和0之间执行4次规则2,实现2邻域边缘像素的标记;接着在细胞1和0之间执行4次规则3,实现4邻域边缘检测.系统运行8步后,在第9步,将膜1中所有标记的边界对象传输到膜2中,膜2的输出即为最后的边缘.zi用于控制膜计算工作的步骤次数.通过以上9步,实现任意分辨率图像在常数步骤内完成图像分割.文中分割结果如图6所示,其中白色像素为计算出的边缘像素.

图6 文献[17]中的实验结果(左:原始图像;右:分割结果)
除了西班牙塞维利亚大学研究团队外,马来西亚理工大学Rafaa等设计了组织P系统[18]用于图像分割,其设计思想和文献[17-18]类似.在文献[19]中,膜系统被应用于6边形图像的区域分割.文献[20-22]报道了用组织型膜系统实现二值图像上的同名区域计算的问题.在国内,西华大学彭宏等也研究了基于组织型P系统的图像区域分割方法,文献[23-24]中报道了他们设计的度为3的组织型P系统,分别对灰度图像和彩色图像进行了处理,并用多幅真实图像进行了测试.
(2) 基于膜优化算法的图像分割
文献[25]提出了膜优化算法,并将其应用于旅行商求解问题,获得了与模拟退火算法相当的效果.在文献[38]中,膜优化算法概括为两类:层次膜结构和网状膜结构膜优化算法.前者包括嵌套膜结构、单层膜结构、混合膜结构和动态膜结构膜优化算法,后者分为静态膜结构和动态膜结构膜优化算法.大量实验结果表明,膜优化算法比相应的启发式算法具有更好的种群多样性和算法收敛性[39].
在基于阈值的图像分割方法中,阈值的计算过程是一个参数寻优过程.因此,可以将膜优化算法应用于基于阈值的图像分割中,如大津法、最大模糊熵法等.这方面的研究主要以国内西华大学彭宏等为主.2012年,他们将最大模糊熵阈值计算方法用膜系统实现,并和采用遗传算法、粒子群优化算法的分割性能进行了实验对比[26].最大模糊熵图像分割准则为在灰度空间搜索一组参数,经该参数分割后图像信息量最大.为求解该优化问题,作者设计了包含2m+1个膜的3层膜系统,如图7所示.膜内的对象为需要求解的参数.第1~m个膜为进化膜,其作用是实现参数的进化;第m+1~2m个膜是每个进化膜对应的子膜,用于存储对应进化膜计算出的局部最优参数;第2m+1个膜为存储全局最优参数的表层膜.系统初始时刻,在每个进化膜中随机产生n个对象,即n个候选解.n个对象中最优参数被存储于对应的子膜,第m+1~2m个子膜中所有参数的最优值被存储在表层膜中.m个进化膜中,采用遗传算法作为进化规则,同时作者对遗传算法中变异算子进行了改进.m个进化膜同时运行,同时将每个膜的局部最优结果传输至对应的子膜,再将所有子膜中最优参数结果传输至表层膜.整个系统以最大执行步数作为停止条件,当系统停止时,表层膜中的对象作为整个系统的输出.在文献[26]中,分割阈值仅1个,需要优化3个参数.随后,他们分别报道了双阈值[27]、多阈值的图像分割方法[28].文献[27]中,分割阈值有2个,可以将图像分为3类目标,需要优化的变量有5个.该文中采用的膜结构和进化规则同文[26].文献[28]中,膜结构仍同文献[26],只是进化规则改为速度-位移模型.另外,在文献[28-29]中,作者给出了膜系统执行步骤的详细过程,分析了用膜系统并行运算后需要的时间复杂度.
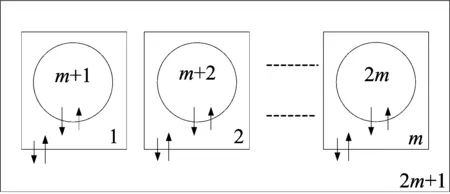
图7 文献[9]设计的膜系统
除此以外,文献[29]给出了一种由教学优化算法启发的膜计算方法(membrane computing inspired teacher-learner-based-optimization,简称MCTLBO),用于求解图像分割中最优的多阈值问题,以4个基准数据库中的图像为测试对象,并与教学优化算法(teacher learner based optimization,简称TLBO)、膜计算方法(membrane computing,简称MC)、粒子群优化算法(particle swarm optimization,简称PSO)进行了实验对比.文献[30]设计了带有混合进化机制的膜系统,用于图像阈值分割.所设计的膜系统采用遗传算法和粒子群算作为进化规则,用通信规则和转运规则实现膜之间的信息交换,从而增强系统种群的多样性,提高算法的收敛性.文献[31]提出了一种基于膜计算的改进遗传算法图像分割方法,设计了一个3层膜的细胞型P系统,各个膜通过运行进化规则和交流规则进行参数寻优.文献[32]提出一种基于P系统的图像阈值分割方法.到目前为止,国内在该方向上已产生了3篇硕士学位论文[33-35].
3.2.2 立体匹配
立体匹配是场景3维重建的基础.立体匹配是指两幅同名图像,对第1幅图像上的每个像素,计算出在第2幅图像上的同名点.由于每个像素对应的搜索区域都在一条极线上,因此,立体匹配算法的时间复杂度随分辨率增加呈多项式增长.文献[36]讨论了P系统实现立体匹配中对称动态规划匹配算法(symmetric dynamic programming,简称SDPS)的能力,设计了SDPS的P系统,给出了系统初始化、进化规则等.
3.2.3 图像配准
图像配准是指将不同时间、不同传感器或不同条件下采集的两幅图像进行匹配叠加的过程.文献[37]提出了基于膜计算的多模态图像配准算法.他们设计一种细胞型P系统的膜结构,细胞膜中1个对象表示1组浮动图像变换参数,每个基本膜采用遗传算法进化对象获得最优变换参数,并将最优对象转运到上层膜中,同时所有基本膜之间随机进行最优对象转运操作.通过以上2种转运操作,上层膜保留本膜中本次进化的全局最优对象,并将其转运到各子膜中,参与各子膜的进化.最终,整个P系统的最优变换参数保留在表层膜中.文献[38]也进行了类似报道.
3.2.4 图像分解与重建
膜算法是元启发式搜索方法、膜系统层次或网状膜结构和进化规则有机结合的混合优化算法.文献[39]设计了量子启发膜算法,将其应用于图像稀疏分解和图像重建,并应用Lena和Cameraman图像测试了算法性能.使用一个非对称原子来构造一个超完整的图像原子字典.通过旋转、平移和缩放基本的非对称原子,得到了原子.背包问题和图像稀疏分解分别是组合和数值优化问题.将膜计算的框架和规则与QIEA(quantum-inspired evolutionary algorithm)的进化机制相结合,被证明是有效的.在MAQIS(membrane algorithm with quantum-inspired subalgorithms)中,二进制字符串对应于问题的候选解决方案.规则的集合负责系统的演变.在膜结构中适当地安排了物体和规则.在此系统中,在表层膜上进行初始化、观察和评价的过程,在几个基本膜中执行生成子代的Q-gate更新过程.对MAQIS来说,适当的组件选择对于算法性能是非常重要的.同时,值得指出的是,MAQIS也可以用其他的元启发式搜索方法来构建,如遗传算法、微分进化、粒子群优化和分布算法的估计等.
4 结束语
自然计算应用于图像处理有着高度并行、可用自然计算的数据结构对图像进行编码的特点[13],近年来受到了大量学者的关注.尽管目前膜计算已成功用于解决图像处理中一些问题,但是仍处于初期的探索阶段,值得进一步深入研究.作者认为未来的研究可以考虑如下几点:
(1) 设计图像处理基础子算法专用的膜系统.目前,研究者需要同时掌握膜系统和图像处理知识才能搭建相应的并行计算平台,如果能设计出相关图像处理子算法的通用膜系统模型,则可大大降低图像处理领域人士应用膜系统的门槛.
(2) 探索复杂图像处理算法膜系统实现方法,如特征提取、特征匹配、三维重建、目标识别等.已有的研究尚集中在用简单的细胞型、组织型膜系统实现简单的低层图像处理算法,未来的研究可以考虑用更复杂的膜系统模型去实现更复杂的图像处理算法.
(3) 构建能运行与评估膜计算方法的平台,研究者仅需要把新提出的方法按照一定的格式或语言要求,把自己模块导入平台,即可给出评估效果.
参考文献:
[1] HARMON L D, KNOWLTON K C. Picture processing by computer[J]. Acm Computing Surveys, 1969, 164 (3875): 19-29.
[2] 王飞宇. 多核图像处理平台及其在夜视图像融合中的应用[D]. 南京: 南京理工大学计算机科学与工程学院, 2015.
[4] 张一栋. 一种新的图像分割算法[D]. 无锡: 江南大学计算机科学与技术学院, 2008.
[5] 章毓晋. 图像处理和分析[M]. 北京: 清华大学出版社, 1999
[6] 张葛祥, 潘林强. 自然计算的新分支-膜计算[J]. 计算机学报, 2010, 33 (2): 208-214.
[7] 张葛祥. 膜计算: 理论与应用[M]. 北京: 科学出版社, 2015.
[10] REINA-MOLINA R, DAZ-PERNIL D, GUTIRREZ-NARANJO M A. Cell complexes and membrane computing for thinning 2D and 3D images[C]//In Proceedings of the Tenth Brainstorming Week on Membrane Computing, 2012: 167-186.
[11] LIU L. 3D thinning on cell complexes for computing curve and surface skeletons[D]. Saint Louis: School of Engineering and Applied Science of Washington University in Saint Louis, 2009.
[12] CHRISTINALH A, DAZ-PERNIL D, REAL P. Region-based segmentation of 2D and 3D images with tissue-like P systems[J]. Pattern Recognition Letters, 2011, 32 (16): 2206-2212.
[14] REINA-MOLINA R, CARNERO J, DAZ -PERNIL D. Image segmentation using tissue-like P systems with multiple auxiliary cells[J]. IMAGE-A, 2011, 2 (4): 25-28.
[16] CARNERO J, DAZ-PERNIL D, MOLINA-ABRIL H, et al. Image segmentation inspired by cellular models using hardware programming[J]. IMAGE-A, 2010 (1): 143-150.
[17] CHRISTINAL H A, BERCIANO A, DAZ-PERNIL D, et al. Searching partially bounded regions with P systems[C]// In Proceedings of the Third International Conference on Soft Computing for Problem Solving, 2014: 45-54.
[18] YAHYA R I, HASAN S, GEORGE L E, et al. Membrane computing for 2D image segmentation[J]. Int J Advance Soft Compu, 2015, 7 (1): 35-50.
[19] ISAWASAN P, VENKAT I, SUBRAMAINIAN K G, et al. Region-based segmentation of Hexagonal digital images using membrane computing[C]//In Proceedings of the 2014 Asian Conference on Membrane Computing (ACMC), 2014: 1-4.
[20] ALSALIBI B, VENKAT I, SUBRAMANIAN K, et al. A bio-inspired software for homology groups of 2D digital images[C] // In Proceedings of the 2015 Asian Conference on Membrane Computing (ACMC), 2015: 1-4.
[22] CHRISTINAL H A, JURADO P R. Using membrane computing for obtaining homology groups of binary 2D digital images[C]// International Workshop on Combinatorial Image Analysis, 2009: 383-396.
[23] PENG H, YANG Y, ZHANG J, et al. A region-based color image segmentationmethod based on P systems[J]. Science and Technology, 2014, 17 (1): 63-75.
[24] 杨雨凡. 基于膜计算的图像区域分割方法研究[D]. 成都: 西华大学计算机与软件工程学院, 2013.
[25] NISHIDA T Y. An approximate algorithm for NP-complete optimization problems exploiting P systems[C]//In Proceedings of the Brainstorming Workshop on Uncertainty in Membrane Computing, 2004: 185-192.
[26] ZHANG Z, PENG H. Object segmentation with membrane computing[J]. Journal of Information & Computational Science, 2012, 9 (9): 5417-5424.
[27] PENG H, SHAO J, LI B, et al. Image thresholding with cell-like P systems[C]// In Proceedings of the Tenth Brainstorming Week on Membrane Computing, 2012: 75-88.
[28] PENG H, WANG J, PREZ-JIMNEZ M J. Optimal multi-level thresholding with membrane computing[J]. Digital Signal Processing, 2015, 37 (1): 53-64.
[29] SINGH V P, PRAKASH T, RATHORE N S, et al. Multilevel thresholding with membrane computing inspired TLBO[J]. International Journal on Artificial Intelligence Tools, 2016, 25 (6): 30-51.
[30] LIU S, ZHOU K, ZENG S, et al. An image threshold segmentation algorithm with hybrid evolutionary mechanisms based on membrane computing[C]// In Proceedings of the Bio-Inspired Computing-Theories and Applications, 2016: 85-94.
[31] 谢佩军. 一种基于膜计算的遗传算法图像分割方法[J]. 工业控制计算机, 2015, 28 (4): 92-94.
[32] 周斌. 一种基于P系统的图像阈值分割方法[J]. 西华大学学报 (自然科学版), 2012, 31 (6): 39-42.
[33] 覃伟明. 基于进化膜计算的图像分割优化方法研究[D]. 绵阳: 西南科技大学计算机科学与技术学院, 2012.
[34] 王浩. 基于膜计算的图像分割方法研究[D]. 成都: 西华大学计算机与软件工程学院, 2012.
[35] 张加容. 由膜计算启发的聚类算法及其在图像分割中的应用[D]. 成都: 西华大学计算机与软件工程学院, 2015.
[36] GIMEL F G, NICOLESCU R, RAGAVAN S. P systems in stereo matching[C]//International Conference on Computer Analysis of Images and Patterns, 2011: 285-292.
[37] 李兆延, 张铖方. 基于膜计算的多模态图像配准算法研究[J]. 西华大学学报 (自然科学版), 2015, 34 (5): 7-15.
[38] 耿龙, 葛丽霞, 张铖方. 基于膜计算的图像配准方法比较研究[J]. 现代计算机, 2016 (23): 69-74.
[39] ZHANG G, GHEORGHE M, LI Y. A membrane algorithm with quantum-inspired subalgorithms and its application to image processing[J]. Natural Computing, 2012, 11 (4): 701-717.
[38] ZHANG G, GHEORGHE M, PAN L, et al. Evolutionary membrane computing: a comprehensive survey and new results[J]. Information Sciences, 2014, 279: 528-551.
[39] ZHANG G, CHENG J, GHEORGHE M. Dynamic behavior analysis of membrane-inspired evolutionary algorithms[J]. International Journal of Computers, Communications & Control, 2014, 9 (2): 227-242.
[40] 冈萨雷斯. 数字图像处理[M]. 北京: 电子工业出版社, 2005.
