基于灰色预测GM（1,1）模型的房地产价格金融分析

文/夏德延，安徽财经大学金融学院

房地产业与人们的生活息息相关，也一直是全社会关注的焦点问题，随着社会的进步和发展，房地产业成为了人们投资和投消费的一大热门[1]，同时也是中国经济的支柱产业。2002年起，中国的房地产价格一直以较快的速度上涨, 到2015年, 全国住宅销售价格上涨了约2倍, 部分大型城市甚至上涨了3—4倍。房地产价格的迅速上涨给我们抛出了一个值得关注的问题，那就是如何准确的衡量房地产价格的变动趋势，这就涉及到模型的建立和对未来的预测。

在对房地产价格的预测上，很多国内外学者都曾采用了不同的方法进行考量。土耳其研究员赛利姆将神经网络以及Hedonic回归模型相结合，选用了土耳其的房地产价格作为样本进行的预测，模型结果表明土耳其的房价仍然体现为上升趋势。哈什米等人认为房地产价格数据是不规则的，处于非线性状态，因此他们放弃了传统的线性方法，将小波神经网络和 BP 神经网络应用于房地产价格指数预测中。中国学者陈娟曾以面板数据非线性平滑转移模型为基础，建立特色的房地产价格指数模型，探讨了房地产价格与影响因素之间的联动性关系。专家袁芳等则运用ARIMA模型，对短期的西安房地产价格做出了精准预测。

不同于以上的方法，本文主要考虑了房地产价格的金融波定性特点，以2002—2015年合肥市房地产价格为原始数据，对房产价格的序列水平值使用灰色模型GM(1,1)模型进行模拟，得以分析合肥房地产价格与各个影响因素之间的灰色关联度，得到未来房产价格的预测值。建立灰色预测模型后，对所得线性方程式进行残差和关联度检验，验证预测的准确性、合理性。本文主要通过灰色预测模型GM（1,1）的运用为合肥市房地产价格走势提供科学合理的分析，并通过所得到的预测数据，对合肥市房地产业的发展提出行之有效的意见和建议。

1 灰色预测模型建立方法

1.1 灰色系统

灰色系统是在1982年由我国专家邓聚龙先生提出的。他提出灰色系统就是指在某个系统里一些信息已知并可以定性或定量分析，但另一些信息却是未知的。灰色系统理论详细的描述了所有的随机过程都可以被当成在一定时空范围内变化的灰色过程,随机变量可看作是灰色量。在灰色系统理论里，无规律的离散数列实际上是有规律序列的一种潜在表现, 通过模型变换可以将无规律的数列转换为满足灰色建模条件的有规律序列。因此，灰色系统理论是从一个整体的角度出发去探讨所有已知和未知信息之间的联动性关系，也就是研究如何使用已知的信息来判定或预测未知的信息。灰色预测方法基于微分方程的建立,它包括系统模型建立、系统数据预测、模型可行性分析等方面。历史研究表明, 在实际使用过程中大多采用一阶灰色模型预测方法, 即GM (1,1)模型。灰色GM(1,1)模型之所以被广泛使用，一方面是因为它所需要的数据很少（一般情况下四个数据就可以建立模型），建模工作量小，同时它的检验结果是非常准确和贴合实际的，同时灰色模型可以进行检验和修正。

1.2 灰色预测GM(1,1)模型简述

灰色GM(1,1)模型是灰色系统理论的核心内容，它通过已知的数据，将系统信息抽象的概念量化，再将量化的概念模型化，最后进行模型优化预测部分未知的数据。模型将系统内已知的数据信息命名为白色，需要进行预测的数据信息命名为灰色，将显化的过程命名为白化过程。灰色预测方法贴合实际，有着非常重要的现实意义，它主要按照如下的步骤进行模拟：

（1）数据的区间检验。使用灰色GM(1,1)模型进行预测时，第一步就是要进行区间检验。一般建模的数据序列的所属区间，要使用覆盖公式来判别。区间合适的数据可以用来建模。

（2）计算一次累加序列。设原始的数据信息为序列代表t时刻的原始数据，一般为非负值。历史信息表明，对原始数据列进行一次累加生成的一次累加序列可以淡化了原始信息数据序列的随机和不平稳性，并且，累加的次数越多，这种淡化的效果也就越显著，数据的随机性也就越小。因此，为了得到随机性小的、规律性强的序列，更好的建立微分方程，我们对原始数据进行一次累加，得到一次累加数列。

（3）平滑性检验。一般大多数的一次累加数据列仍然是稳定性弱的,不一定满足我们的建模要求,因此，在建模之前，需要对数列做平滑性检验。若原始数据列 满足平滑比为减函数的要求，那么原始数列为平滑函数，符合建模条件。

（4）指数规律检验。灰色GM(1,1)模型在本质上是使用指数规律来模拟原始数据序列的变化情况,因此需要对原始数据序列的一次累加序列进行指数规律的检验。设，若序列满足指数规律，可以建模。

（5）建模步骤

给定一个灰色GM(1,1)模型,与之对应的微分方程为:记方程的系数向量为,使用最小二乘法求解可知：

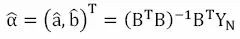
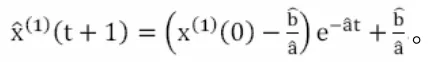
1.3 模型检验

灰色系统GM(1,1)模型的精确性检验，主要包括残差的检验和关联度的检验[2]。一般来说，残差越小，也就表明预测值和实际值之间的差值越小，拟合程度越好；关联度越大，表明模型和原始序列之间的相关性越大，模型越贴合实际。

（1）残差检验

根据上述得到的模型，算出一次累积序列，并将做一次累减生成。同时设为残差，为相对误差，则有：

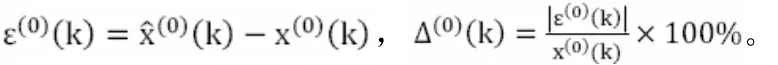
通过观察、的大小，可以很直观的检验模型的准确性。残差和相对误差越小，模型越准确。

（2）关联度检验

关联度检验是指对时间序列数据进行几何关系对比，图像形状越接近，原始数据和预测数据就越贴合，取分辨系数为0.5，记关联系数为C和，关联度为，则：

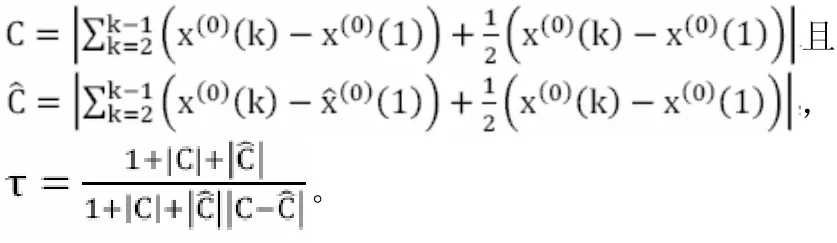
2 合肥市房产价格实证分析

本文采用2002年—2015年的合肥房价数据（所有数据来自中国统计年鉴）[3]，可以得到合肥市房价的原始数据序列为：在建模之前进行如下检验：

（1）进行平滑性检验。平滑比，故，显然平滑函数为减函数，样本满足平滑性。

（2）进行指数检验。，有，当t>3时，，满足指数规律，可建立GM(1,1)模型。

建模步骤如下：

累加矩阵，常数项为，，所以样本数据的GM模型为。

建立好模型以后，需要进行模型的检验。利用模型预测2002—2015年合肥市的房价,并与每年实际价格进行对比得出不超过2 00，维持在0.1%以下，我们可以看出实际结果和预测结果之间的残差和相对误差是非常小的，几乎可以忽略不计，说明模型的拟合程度较优，接下来进行关联度分析。计算可得

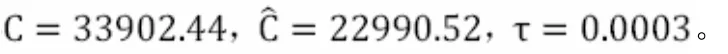
该模型关联系数 符合实际检验要求，因此其预测是稳定且平滑的,证明该模型是显著有效的，可以用于合肥市今后各年房地产价格的中长期预测。

3 总结

根据实证结果, 发现合肥市未来的房价仍然会以一个较快的速度上升，这对政府的发展以及人民的生活产生举足轻重的影响，房地产价格的合理调控成为一个必要的环节。在此基础上,针对目前的房地产的价格调控问题提出以下建议:

第一，进行相关法律的完善。一方面是要从根本上控制贷款的过度投放，以法律的强制性规范目前的贷款制度，合理的调整个人住房贷款政策，提高贷款的条件和首付比例，并保证这一控制措施的有效性。另一方面要控制个人可购住宅数，合理控制“炒房”这一不良现象。

第二，政府应该进一步加大管理，发挥核心领导作用,严控预售环节，对开发商预售价格不实、操控价格、提前预售等行为施行延缓其销售、停售等强制措施。

第三，政府有义务建立住房有效保障体系。政府应继续扩大城乡住宅建设的开发力度, 给予一定的优惠条件来鼓励开发商更多投向这一方面的建设，使购房的门槛得以降低，真正解决很多人“买房难、住房难”的问题，从而缓解中低收入家庭的住房问题，控制开发商的不良抬价行为。

第四，目前，中国的城市化水平仍较为滞后，农村建设与发展水平低，导致大量人员流出，转向城市。这不仅不利于乡镇的发展，更是极大程度的增加了城市流动人口压力。因此，加强农村建设，实行城乡统筹的战略，一方面有利于扩大内需，促进区域经济的发展，一方面减轻住房压力，稳定房价。

【参考文献】

[1]李春吉,孟晓宏.中国房地产市场结构和价格影响因素的实证分析[J].产业经济研究,2005(6):48-56.

[2]张翠莲,张钦礼,何春江.灰色系统理论在河北省居民人均年收入预测中的应用[J].数学实践与认识,2005(4):63-66.