基于模糊推理的无人车路径跟踪算法

焦纪超

（长安大学 汽车学院，陕西 西安 710064）

前言

智能车辆作为一个复杂非线性系统，其运动控制一直是重点和难点，智能车辆的路径跟踪系统是指控制智能车稳定准确地跟踪参考路径。目前在无人车运动控制领域比较成熟的控制算法分为预瞄式和非预瞄式[1]两种，前者是将车辆前方的道路曲率作为输入，以车辆与参考路径的航向偏差作为控制目标，通过各种反馈控制方法如滑模变结构控制、H∞控制方法等算法设计反馈控制；后者是根据期望路径和车辆的动力学参数计算出期望的车辆运动物理量，进而进行跟踪控制。运动控制是整个智能车系统最底层的执行部分，它关系到智能车辆能否准确地执行规划层所给的任务，但智能车辆在运行过程中受到路面、风力等外部影响以及本身系统的不确定性的影响。因此，如何设计鲁棒性强的控制算法一直是智能车领域的研究热点。

1 车辆阿克曼转向模型

当车辆在平直道路上中低速行驶时，忽略轮胎侧偏以及悬架侧倾的影响，可以将车辆的两前轮和两后轮分别合并成一个车轮，这样可以较为简单的分析车辆转向过程中前轮转角和车辆瞬时转弯半径的关系，该简化模型称为自行车模型，简化方式如图1所示。

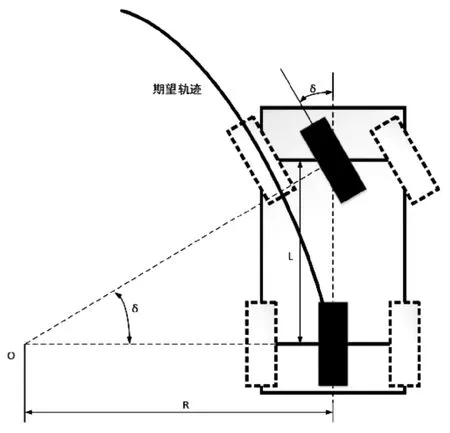
图1 阿克曼转向示意图

图1中δ为前轮转角，R为转弯半径，L为轴距，由图1的几何关系可以得到如下关系式：

式中，k为道路曲率，为半径R的倒数。

2 纯跟踪控制策略

纯跟踪算法是一种经典的路径跟踪算法[2]。图2是传统的纯跟踪控制策略示意图，点P为车辆前方并位于参考路径上的一点，称为预瞄点；该点与车辆后轴中心点距离为 ld，称为预瞄距离；该点距车辆中心线的距离为ed，称为横向预瞄偏差，图中α为预瞄点P与车辆后轴中心点连线与车辆中心线的夹角。该算法的原理是假设车辆在某一时刻为了追踪到点 P，走过了一段圆弧，改短圆弧的半径为 R，则由图 2中的几何关系可得：

结合（1）（2）（3）式可得如下关系：

图2 纯跟踪原理图

纯跟踪算法在实现路径跟踪时简单有效，但也有一定的缺点，即预瞄距离受车速的影响比较大，如果预瞄距离过小，则对道路的曲率变化过于敏感，方向盘转角容易发生突变，在车速较高时车辆稳定性较差，如果预瞄距离过大，跟踪精度就会大大下降，因此本文提出了一种基于模糊推理的可变预瞄距离的智能车辆路径跟踪算法，该算法通过模糊推理机制计算出合理的预瞄距离兼顾了车辆在低速时的跟踪精确性和高速时的车辆稳定性。

3 模糊推理机的建立

模糊推理是一类应用模糊集合将理论的推理和控制方法[3]，模糊推理的优点是不需要考虑车辆实际的结构以及动力学特性，如果规则制定的合理，将会产生很好地控制效果。本文设计了一种二维的模糊推理机，把车速和纵向加速度作为输入，把预瞄距离作为输出，这样在低速时减小预瞄距离，提高路径跟踪的精度，在中高速时增加预瞄距离，防止方向盘转角发生突变，保持车辆在中高速时的稳定性和乘坐舒适性。

选择车速的模糊语言变量为V，由于只考虑中低车速，V的论域为{0,10,20,30,40,50,60}，单位为km/h；车辆纵向加速度模糊语言变量为A，其论域为{-3，-2，-1,0,1,2,3}，单位为m/s2；预瞄距离模糊语言变量为LD，论域为{0，2.5，5，7.5，10，12.5，15}，单位为m。设定三个模糊变量的语言值均为{PB,PM,PS,ZO,NS,NM,NB}共7挡。为了简化算法，采用标准的三角形隶属度函数。确定各变量论域以及隶属度函数以后，再确定模糊推理规则。模糊推理规则的制定原则为：车速越高，加速度越大，预瞄距离就越大，反之则越小。这里共总结了49条模糊推理规则，制定了模糊推理规则表，如表1所示。

表1 模糊推理规则表

由模糊推理机制得出的预瞄距离是一个模糊子集，需要进行解模糊化。本文采用重心法进行解模糊化操作。所谓重心法就是取模糊隶属函数曲线与横坐标围成的面积的重心作为代表点，即计算出范围内一系列连续点的重心，如式5所示。

4 仿真实验

为了验证本文提出的算法的有效性，利用 Simulink/CarSim平台进行联合仿真实验，将本文算法与传统的纯跟踪算法进行对比。实验采用CarSim软件中自带的道路“Alt 3 from FHWA”和自带的车型“E-Class，Sedan”。

图3 0到60km/h车速下两种算法横向偏差对比

图4 50km/h车速下两种算法横摆角速度对比

整个实验过程如下：使车辆速度从0缓慢加速到60km/h，分别在传统算法和本文的改进算法的控制下跟踪参考路径，输出车辆前轴中心点距道路中心线的横向距离，即横向偏差和车速在 50km/h时两种算法的车辆横摆角速度对比，在这里传统算法预瞄距离取得是 6m，实验证明在这个预瞄距离下传统算法路径跟踪效果较好，改进算法在整个过程中模糊控制规则不变，结果如图3和图4所示。

5 结论

有上述仿真结果可以得出以下结论：当车辆从0加速到60km/h过程中，改进算法在车速较低和较高时跟踪精度均优于传统算法，在中等车速下略差于传统算法；在 50km/h的车速下，车辆的横摆角速度小了很多，即增加了车辆的横向稳定性。因此，基于模糊推理的改进纯跟踪算法既能保证跟踪精度，又可以增加车辆的稳定性和舒适性。

参考文献

[1] 赵熙俊,陈慧岩.智能车辆路径跟踪横向控制方法的研究[J].汽车工程,2011,33(05)∶382-387.

[2] Li X, Sun Z, Chen Q, et al. An adaptive preview path tracker for off-road autonomous driving[C]. international conference on control and automation, 2013∶ 1718-1723.

[3] 蔡自兴.智能控制原理与应用[M].北京∶清华大学出版社,2014∶73-96.