基于标签和评分差值信息熵的协同过滤算法
2018-05-23侯继昌陈家琪
侯继昌,陈家琪
(上海理工大学 光电信息与计算机工程学院,上海 200093)
随着信息时代的发展,人们逐渐步入了信息过载的时代,推荐系统应运而生。协同过滤算法[1-3]是推荐系统中最成功的技术,传统的协同过滤算法仅仅考虑到用户之间共同评分项的评分信息,没有考虑到用户的兴趣,此外用户共同评分项目较少,数据稀疏性[4]较大,因此通过传统方法得到相似用户集的准确性和可靠性难以得到保证。
针对上述问题,研究者们提出了很多解决方法。文献[5]提出了基于信息熵的协同过滤算法,利用用户评分信息熵来反映用户评分分布和倾向程度;文献[6]提出基于加权信息熵相似性的协同过滤算法,通过差异值和共同评价数目对信息熵进行加权再进行归一化处理计算项目间的相似度。此外,很多学者开始关注标签,认为标签作为用户兴趣和资源特征的一种表达方式,可以展现出用户兴趣。文献[7]提出基于社会化标签的协同过滤算法,利用群体智慧选择流行标签对用户和资源建模;文献[8]提出基于标签和协同过滤的个性化资源推荐,依据标签计算用户偏好程度和资源特征相似度;文献[9]提出基于标签和协同过滤的个性化推荐算法,通过标签来学习用户对于资源的兴趣以及计算资源的相似度,再预测用户对于其它资源的偏好值,最后实现资源推荐。
鉴于现有相似性度量方法存在的不足,本文探讨一种基于标签和评分差值信息熵的协同过滤算法。从评分差值信息熵和用户标签两个方面来计算用户评分和兴趣相似度,来获得更好的推荐效果,改善数据稀疏问题。
1 相关工作
1.1 基于用户的协同过滤算法
基于用户的协同过滤算法[10]主要是找出目标用户的相似用户集,为目标用户推荐Top-N的相似度用户。
1.1.1 相似度计算
相似度计算是传统协同过滤算法的关键。常见的相似度计算方法[11]有Pearson相似度、Jaccard相似度和Cosine相似度,如式(1) ~式 (3)所示。
(1)
(2)
(3)
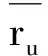
1.1.2 传统评分预测方法
传统的预测目标用户u对未评分项目i的评分公式[12]为
(4)
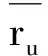
1.2 信息熵定义
信息熵是衡量分布的混乱程度或分散程度的一种度量[13]。分布越分散,信息熵就越大;分布越有序,信息熵就越小。对于给定的样本集X,其信息熵的计算公式为
(5)
其中,n代表样本集X的分类数,p(xq)代表X中第i类元素出现的概率。信息熵越大表明样本集X分类越分散,信息熵越小则表明样本集X分类越集中。当X中n个分类出现的概率一样大时(都是i/n),信息熵取最大值log2n;当X只有一个分类时,信息熵取最小值0。
2 用户标签兴趣遗忘的相似度计算
标签可以作为用户兴趣的体现,可被用户依照个人偏好进行自由资源标注。因此,本文在用户间评分相似度的基础上,把用户标签作为用户兴趣体现点,同时考虑到用户对标签的兴趣会随着时间的变化而漂移的。因此,利用非线性遗忘函数对用户标签向量进行改进,然后利用Cosine相似度计算方法来计算用户标签向量相似度,进而获取用户兴趣相似度。
2.1 引入非线性遗忘函数计算用户标签向量
2.1.1 用户的标签权重向量
用户的标签特征向量是利用用户常使用的标签来表示用户的兴趣特征,记为
(15)
其中,w(u,ti)=TFutiIDFuti,TFuti为用户u对资源使用标签ti进行标注的频率,即用户u对资源标注标签ti的次数除以用户u标注的总次数;IDFuti表示标签ti关于用户的逆向文件频率,即用户总数m除以标注标签ti的用户总数,再对得到的商取对数。
2.1.2 引入的非线性逐步遗忘函数
用户对标签的兴趣不是不变的,根据心理学遗忘规律,用户对标签的兴趣是会随着时间逐步衰减的。此外,人的遗忘过程不是简单的逐步遗忘。遗忘规律表明:在识记后的短时期内遗忘进行得较快,经过足够长的时间间隔后遗忘进行得比较缓慢,即遗忘过程是先快后慢,是非线性的。文献[14]提出非线性逐步遗忘函数,来形容遗忘现象。因此,本文将非线性遗忘函数应用到用户对标签的兴趣中去,来表示用户的兴趣变化。
基于用户标签的非线性逐步遗忘函数为
(16)
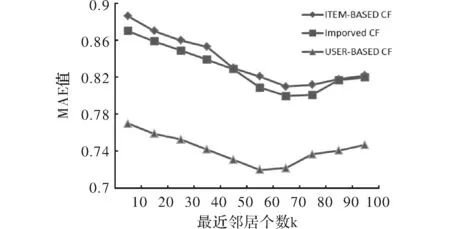
其中,0≤m≤1,0 2.1.3 引入非线性遗忘函数后的用户标签向量 引入非线性遗忘函数,得到修正的用户标签向量 (17) 本文采用余弦相似度来计算用户之间的标签向量相似度如式(18),以此来判断用户兴趣相似度 (18) 传统协同过滤算法仅利用评分数值信息来刻画用户之间的相似性,但是,由于用户评分数据极端稀疏,因此传统的相似度计算对于刻画用户之间的相似性准确度较低。本文提出基于评分信息熵的相似度计算方法,来改善数据稀疏问题并提高推荐质量。首先计算用户评分的信息熵,过滤噪点数据,其次引入Jaccard系数(用户之间共同评分项目所占比)计算用户评分差值信息熵并结合PCC方法来计算用户评分之间相似度。 定义1[13]假设用户u的评分是一个离散的评分集Ru={Ru1,Ru2,Ru3,…,Run},Rui为用户u其中一个评分,在此限定评分范围为1 ~ 5,则用户u上评分为Rui的概率分布函数p(Rui)等于评分为Rui的项目个数占用户u已评分项总个数的比率。 用户评分之间的信息熵 (6) 由式(6)可知,评分的信息熵H(Ru)只与评分值Rui的概率分布有关,而与评分值无关。因此,利用用户评分信息熵过滤评分信息较少的用户,避免噪声数据的干扰,例如:评分为(1,1,… ,1)的用户数据。系统中的用户对推荐引擎的作用效果不同,有的用户提供的评分所含的信息量多有的信息量少,过滤信息量少的用户可以有效提升推荐精度。 为了过滤掉噪声数据,首先确定一个评分信息熵阈值τ,即当H(Ru) <τ时,则可以过滤掉用户u的评分信息。τ需要通过实验验证获得,合理地选择τ可以有效提高推荐精度。 3.2.1 计算两个用户间的评分差值 记用户u和用户v的共同评分项目集合为Iuv={i1,i2,i3,i4,…,in},用户u共同项目评分数据为ru={rui1,rui2,rui3,…,ruin,},用户 共同项目评分数据为rv={rvi1,rvi2,rvi3,…,rvin,}。则这两个用户的评分数据的差值集合D-value(rui,rvi)可以定义为 D-value(rui,rvi)={d1,d2,…,dn} (7) 其中,dk=ruik-rvik。 用户之间评分差值信息熵D-value(rui,rvi)为 (8) 其中,p(dk)代表在D-value(rui,rvi)中dk的概率大小。 信息熵是反映数据分散程度的一种度量,因此,当用户间评分差值信息熵越小时,用户间的评分倾向越一致;反之,若信息熵越高,说明这两个用户评分倾向越不一致。此外,当两个用户共同评分的项目数很小时,即使他们的评分差值信息熵很小,也不代表二者一定相似,即用户之间的相似度也和共同评分项目有关。因此,考虑到用户评分交集的影响,本文引入参数f,计算公式如下 f=1/J(u,v) (9) J(u,v)为用户之间的置信度函数,本文用Jaccard相似度计算公式表示为 (10) 由上式可知,当用户之间的评分项目交集越小时,置信度函数值J(u,v)越小,进而参数f越大,对应的评分差信息熵值应该越大,用户之间的相似性越小。因此,用户之间的评分差信息熵修正为 (11) 3.2.2 将用户间评分差信息熵进行归一化 式(11)计算所得的评分差信息熵值不在零到一之间,为了后续计算用户之间的相似度,本文采用反余切函数转换来做归一化处理,如下 (12) 本文添加对用户间评分分值相似度的计算。本文采用PCC相似度计算方法,如式(13)所示。 (13) 综上,本文最终基于用户评分的相似度计算方法为 (14) 结合基于用户评分的相似度和用户之间的兴趣相似度,得到最终的用户相似度计算公式 (19) 式 (19) 中:入的值在0 ~ 1变化,simend(u,v)代表用户之间的最终相似度。用式 (4) 来预测用户对未评分的项目的评分,产生Top-N推荐。 基于信息熵和标签的协同过滤算法的流程如图1所示。 图1 基于信息熵和标签的协同过滤算法的流程 输入用户的标签信息,用户项目的评分信息。 输出目标用户u对待评分项目i的预测评分。 a) 根据用户项目评分信息利用式 (6) 来计算信息熵,设置阈值τ,来过滤噪点; b) 利用用户u与其他用户v之间的评分差值计算差值信息熵,并结合PCC来获取最终的基于评分的相似度simrate(u,v); c) 利用用户的标签信息,引入非线性遗忘函数来构建用户标签向量; e) 利用式 (19) 计算用户最终的相似度simend(u,v)形成目标用户u的候选邻居集合Su; f) 通过集合Su和式 (4) 计算出目标用户u对项目i的评分,产生Top-N推荐 本文采用GroupLens 站点提供的 MovieLens 10 MB数据集验证基于信息熵和标签的协同过滤的推荐算法。数据集中用户数超过70 000,标签数超过90 000个,评分数据集较大,因此本文抽取其中6 000名用户的评分记录和标签标注记录进行实验。实验中,先计算用户评分信息熵过滤噪点数据,剩余数据随机分为训练集和测试集,其中训练集占90%,测试集占10%。 平均绝对误差(Mean Absolute Error,MAE)[16]。 MAE用项目预测评分和实际评分间的偏差度量算法的准确性,公式为 (20) 其中,Pui计算得出对项目i的预测评分值,tui为用户对项目的实际评分值;N为待测集中的项目总数。 5.3.1 过滤噪点数据 计算出实验数据集中各个用户的评分信息熵,设置阈值过滤噪点[15]。为了更加准确的确定信息熵阈值,合理地选择信息熵阈值,实验统计出不同信息熵值所对应的用户总数如图2所示。横轴为信息熵,竖轴为用户个数。实验发现用户聚集的疏密分界线的信息熵值约为1.0。因此图2信息熵从0.6开始取值,每次递增0.1,直到1.2为止。可以看出信息熵值在0.6~0.9之间,用户数很少,但当信息熵值>0.9时,用户数量明显增多。因此,设置阈值τ为0.9。过滤掉信息熵小于0.9的用户达到过滤噪点数据的目的,过滤后数据集用户总数为5 653。 图2 信息熵对应的用户数 5.3.2 实验结果 将本文算法和传统的基于用户的协同过滤算法进行比较,MAE值越小,推荐质量越高。但是为了能获取更为准确的推荐,首先需要确定用户相似度计算公式中的λ值,然后,使用最优的λ值进行实验,改变相似用户集k的数量,来观察传统基于用户的算法和本文中非线性衰减函数的m值,根据先前研究定为0.6。接下来,用过滤后的数据集进行实验。 首先,确定λ值。通过改变用户相似邻居个数k,来观察不同λ值下的MAE值,MAE值越小,推荐质量就越高。实验在相似邻居集k为10,20,50的情况下进行,如图3横轴为λ取值,范围是从0到1。竖坐标为MAE值。从图中可以看出,随着λ值得增大,MAE值逐渐减小,当λ值为0.80时,不同k值得曲线的MAE值都达到了最小值,之后,λ值在增大,不同曲线对应的MAE值又开始增大。因此,当λ值为0.80时,MAE最小,推荐效果最好,因此,设置λ值为0.80。 图3 k为10、20、50时,不同λ值下MAE比较 在不同k值的情况下,计算传统基于用户的协同过滤算法、基于项目的协同过滤算法和本文改进算法的MAE值的大小,判断相比于传统算法,本文所改进的推荐算法在推荐质量上是否有所提升。如图4所示,横轴代表相似用户集的k值,纵坐标代表MAE值。可以看出,不同k值得情况下,本文改进算法的MAE值均小于传统算法,当k为70时,本文改进算法的MAE值最小,推荐效果最好,但当k值逐渐增大,MAE值逐渐增大,推荐效果变差,但仍比传统算法推荐效果好。 图4 不同算法MAE值比较 通过实验分析得出,本文改进的算法相比传统的协同过滤算法,提高了推荐的精度,具有更好的推荐效果。 本文引入信息熵和用户标签,并考虑用户对标签的兴趣变化,提出一种基于信息熵和标签的协同过滤算法。该算法更深层地挖掘用户评分信息,并且利用用户标签来表示用户的兴趣,通过引入遗忘函数来表示用户兴趣的漂移,充分考虑到了用户评分偏好等多个因素。实验结果表明,该算法在一定程度上改善了数据稀疏的问题,提高了推荐精度。此外,对非线性遗忘函数中的参数对推荐效果的影响本实验并没有做更多探讨,动态选取参数最优值是否能获取更好的推荐效果,这将是下一步的研究工作。 参考文献 [1] 高娜,杨明.一种改进的结合标签和评分的协同过滤推荐算法[J].南京师大学报:自然科学版,2015,38(1):98-103. [2] 毕孝儒.项目子相似度融合的协同过滤推荐算法[J].计算机系统应用,2015,24(1):147-150. [3] 郝立燕,王靖.基于项目流行度的协同过滤 Top-N 推荐算法[J].计算机工程与设计,2013,34(10):3497-3501. [4] 王兴茂,张兴明.基于贡献因子的协同过滤推荐算法[J].计算机应用研究,2015,32(12):3551-3554. [5] 张佳,林耀进,林梦雷,等.基于信息熵的协同过滤算法[J].山东大学学报:工学版,2016(2):43-50. [6] 刘文龙,张桂芸,陈喆,等.基于加权信息熵相似性的协同过滤算法[J].郑州大学学报:工学版,2012(5):118-120. [7] 王宝林,韩帅帅,张德海.一种基于社会化标签的协同过滤推荐算法[J].电子科技,2015,28(7):90-93. [8] 蔡强,韩东梅,李海生,等.基于标签和协同过滤的个性化资源推荐[J].计算机科学,2014(1):69-71. [9] 刘健,张琨,陈旋.基于标签和协同过滤的个性化推荐算法[J].计算机与现代化,2016(2):62-65. [10] Zhao X,Niu Z,Chen W.Interest before liking: two-step recommendation approaches[J]. Knowledge-Based Systems,2013,48(2):46-56. [11] Gan M,Jiang R.Improving accuracy and diversity of personalized recommendation through power law adjustments of user similarities[J].Decision Support Systems,2013,55(3):811-821. [12] Li X,Roth D.Learning question classifiers: the role of semantic information[C].Beijing:International Conference on Design Automation Conference,2002. [13] 郑先荣,汤泽滢,曹先彬.适应用户兴趣变化的非线性逐步遗忘协同过滤算法[J].计算机辅助工程,2007(2):89-95. [14] 刘江冬,梁刚,冯程,等.基于信息熵和时效性的协同过滤推荐[J].计算机应用,2016,36(9):2531-2534. [15] Medo M,Yeung H C.Recommender systems[J].Physics Reports,2012,519(1):1-49.2.2 计算用户标签向量相似度
3 评分信息熵的相似度计算
3.1 计算用户评分信息熵来过滤噪点数据
3.2 计算用户间评分差值信息熵
3.2 引入Jaccard函数改进用户评分差值信息熵
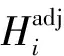
3.3 结合PCC计算用户评分的相似度
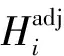
4 基于信息熵和标签的协同过滤算法

5 实验结果与分析
5.1 实验数据
5.2 推荐质量度量标准
5.3 实验结果与分析


6 结束语
