煤与瓦斯突出指标重要性确定及验证方法探究*

鄢朝兴,刘 勇,康向涛,田 燚,韩连昌,冷光海,2

(1.贵州大学 矿业学院， 贵州 贵阳 550025; 2.贵州省盘江精煤股份有限公司土城矿， 贵州 盘州市 553529)

0 引 言

煤与瓦斯突出自煤矿开采以来一直影响和威胁着矿井安全生产，是井下重要灾害之一。随着开采深度不断增加，煤与瓦斯突出现象就愈加明显，而突出的发生与地应力、煤体中瓦斯和煤的物理性质有关。这三个项目又具体表现在地质构造、煤层厚度、煤层中瓦斯压力、煤层埋藏深度、掘进引发的动力现象、煤层倾角、软分层厚度等因素中。如何确定各因素在影响突出上的重要性，国内学者对此各有不同的方法和手段[1]，梁家辉等运用模糊数学法预测煤与瓦斯突出危险性[2]，李成武、许延超等人利用主成分分析法分析了煤与瓦斯突出的主要影响因素[3]。但由于瓦斯突出原理复杂，影响因素较多，各因素之间具有模糊性和不确定性，所以大多数分析不是很理想。本文采用美国运筹学家T. L Satty教授提出的层次分析法，其简单的系统能够较好地将凌乱、看似不相关的数据按照一定原则归类整理成若干层次，然后确定目标进而对各元素采用比较法确定其各指标的重要性。并运用方差分析法检验层次分析法所得结果。

1 层次分析法简介

1.1 层次分析法基本原理

将问题先分解后综合是层次分析法的基本思想。采用定性与定量分析的有机结合来代替主观意识所给出的结果，实现定量化决策。根据结果需求和问题的性质，把需要分析的问题层次化，从上至下分为目标层、中间层和准则层，形成一个类金字塔结构模型，其问题本质归根于最底层相对于最高层重要程度的权值问题[4]。

1.2 APH基本方法与步骤

在运行层次分析法进行决策时，一般分为4个步骤进行[5]。

(1) 分析系统间个因素间的关系，建立系统阶梯层次结构。

(2) 对同一层次的各个元素关于上一层次中某一准则的重要性进行两两比较，构造判断矩阵。

(3) 由判断矩阵算被比较元素对于该准则的相对权重。

(4) 计算各层元素对系统目标的合成权重，并进行排序。

这4个步骤通过以下几点来实现：

(1) 阶梯层次结构的建立。用层次分析法分析问题，首先要明确所要研究的目标，即目标层，将问题层次化，构造阶梯层次结构模型，其中上一层元素对下一层的某些元素起支配作用。这些层次一般可分为3类。目标层：分析问题的预定目标或理想结果，一般只有一个元素。中间层：决策时的备选方案层，实现总目标的中间环节。最底层：实现目标层所要考虑的因素、决策的准则。

(2) 构造判断矩阵。首先进行构造矩阵的方法选择；其次专家进行两两比较判断；再次单个专家对比较元素进行两两比较最后进行综合判断，在层次分析法中为了使决策判断量化，采用九级标度法量化指标，如表1所示。

(3) 对矩阵进行计算，得出矩阵权重并进行一致性检验。

表1 九级标度法

2 层次分析法在确定煤与瓦斯突出因素重要性上的运用

贵州省六盘水市盘县金佳矿是煤与瓦斯突出严重的矿井，自矿井建设以来多次发生过较严重的煤与瓦斯突出事故。全井田基本可采煤层有1， 3， 7， 9， 10， 12， 17， 18八层，均为较稳定煤层；大部分可采煤层有5， 6， 22三层，均为不稳定煤层；部分可采煤层有13， 18-1， 29三层，其中18-1号煤层为较稳定煤层，其它为不稳定煤层。煤层瓦斯含量0.04～22.70 mL/t，各煤层均属高瓦斯煤层。

2.1 影响瓦斯突出的因素

影响煤与瓦斯突出的因素有很多，结合相邻矿井以及历年来经验，选择煤与瓦斯突出具有代表性的因素，如图1所示。

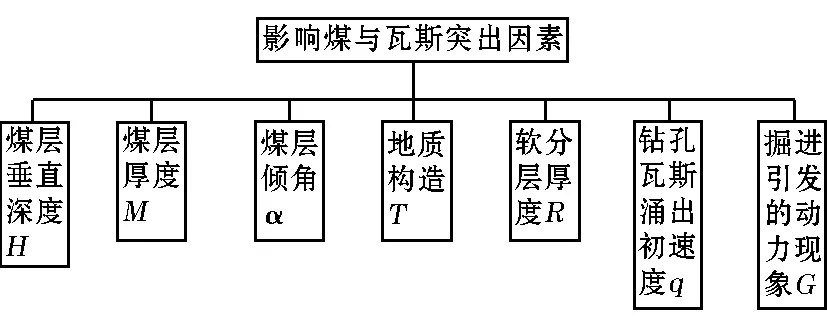
图1 影响煤与瓦斯突出因素

2.2 构造判断矩阵B

构造判断矩阵就是对影响煤与瓦斯突出的因素两两比较，然后根据九级标度法对两因素间重要性进行评定，为了保证评定结果的准确性，一般由相关专家和技术人员完成，经评价比较，金佳矿区煤与瓦斯突出影响因素判断矩阵如表2所示。

求解层次分析法判断矩阵特征值和特征向量的方法有几何平均法、算术平均法、特征向量法等，本文采用算数平均法，其步骤如下：

(1) 计算判断矩阵每一行元素的乘积Mj:

(1)

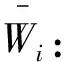
(2)

(4) 最大特征根λmax求解：

(3)

经计算得特征值为λmax=7.6358，特征向量Wi=[0.044,0.0445,0.0619,0.349,0.09,0.096,0.314]。

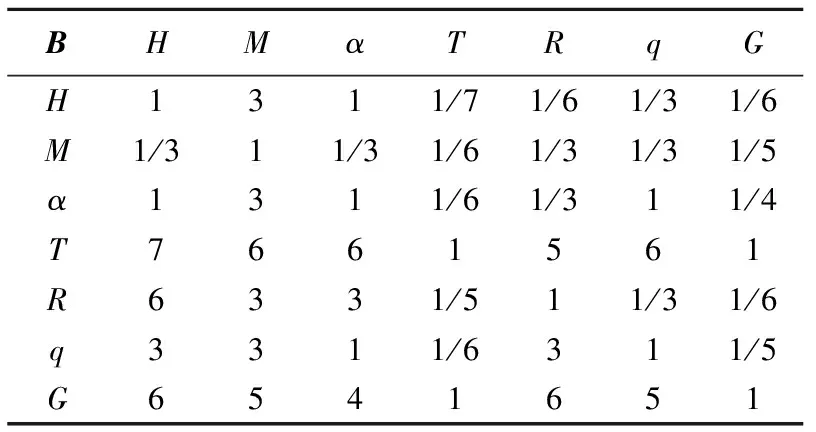
表2 煤与瓦斯突出影响因素判断矩阵

2.3 一致性检验

检验2.2节所求得的向量W是否可以作为特征向量叫作一致性检验，步骤如下：

(1) 平均随机一致性指标RI。平均随机性指标一般来说需要计算，但对于低阶矩阵，平均随机一致性指标可直接查表获得，详情如表3所示。

表3 RI随判断矩阵维数n变化

(2) 计算一致性检验指标CI。

(4)

式中,λmax为判断矩阵特征向量；n为判断矩阵维数。

(3) 求出一致性指标CR。CR作为判断矩阵一致性是否良好的依据，其值大小至关重要，当CR≤0.1时，表明矩阵一致性良好，即矩阵可以作为判断矩阵，如若不然应当对判断矩阵进行适当修正[6-7]。

如上所述，对矩阵一致性进行检验，结果如表4所示。

2.4 权重向量整理排序

由上述分析得知，判断矩阵一致性指标CR为0.08，满足一致性要求，向量W可以作为判断矩阵B的特征向量，即特征向量W里的元素可以作为确定煤与瓦斯突出重要性指标的权重，但权重有大小之分，为了便于观察和分析各因素间的差异性，对权重向量进行排序，如表5所示。

表5 煤与瓦斯突出影响因素权重向量排序

从表5中可以看出，地质构造是造成煤与瓦斯突出的重要原因。

3 层次分析法检验方法探讨

由上述所得，地质构造和采动时的动力现象是影响煤与瓦斯突出的重要指标，本节提出一种确定煤与瓦斯突出指标重要性的方法即方差分析法。

3.1 方差分析法简介

所谓的方差分析法就是设有两因素A、B,A有ɑ个水平：A1，A2，…，Aɑ，B有b个水平：B1，B2，…，Bb为研究交互作用的影响，在每种组合水平(Ai,Bj)下重复做n次(n≥2)试验[8]，每个观察值记为xijk,结果如表6所示。设xijk～N(μij,σ2)，i=1,2,…，a，j=1,2,…，b,k=1,2,…，n,xijk之间相互独立，并设：

xijk=μ+αi+βi+γij+εijk

(5)

式中，μ为总平均值；αi为水平Ai的效应；βi为水平Bi的效应；γij为A和B交互作用的效应。εijk～N(0,σ2)且相互独立。对于这个模型检验下面的假设：

(6)

(7)

(8)

然后计算出各因素、误差以及总平方和SA,SB,SA×B,SE,ST。其中：

(9)

(10)

(11)

(12)

SE=ST-SA-SB-SA×B

(13)

然后列出方差分析表，如表7所示。

表6 试验指标观察值

表7 方差分析

然后再根据已知的α值查出：

Fα(a-1),ab(n-1),Fα(b-1,ab(n-1)),Fα((a-1)(b-1),ab(n-1))。

通过与已求得的F1,F2,F3对比后得出拒绝域，从而得出各因素对实验的重要性以及因素间的交互作用对实验的影响。判断依据如下：

如果F1≥Fα(a-1),ab(n-1),则拒绝HA0,因素A有显著影响。

如果F2≥Fα(b-1,ab(n-1)),则拒绝HB0,因素B有显著影响。

如果F3≥Fα((a-1)(b-1),ab(n-1)),则拒绝HAB0,因素A×B有显著影响。

3.2 方差分析法运用分析

以影响煤与瓦斯突出的因素的其中两个因素(软分层厚度以及煤层倾角)作为方差分析法的运用分析。

专家和有经验的工作人员对不同软分层厚度和煤层倾角对影响煤与瓦斯突出重要性进行评分，评分分为4个等级(Ⅰ，Ⅱ，Ⅲ，Ⅳ分别代表极重要、相对重要、一般重要以及不重要)，评分等级标准划分如表8所示。然后将所得评分做好记录，记录结果见表9。

表8 评分等级划分

表9 数据观察记录

这是一个双因素考虑交互作用的实验。设因素评分得分为：

xijk=μ+αi+βi+γij+εijk

原假设：

HA0:α1=α2=α3=α4=0

HB0:β1=β2=β3=0

HAB0:γij=0i=1,2,3,4j=1,2,3,4

备择假设：

HA1:αi≠0至少一个i

HB1:βj≠0至少一个j

HAB1:γij≠0至少一对ij

根据自由度分别计算出SA,SB,SA×B,SE,ST。然后做出方差分析表，如表10所示。

表10 方差分析

然后再根据已知的α值查出:

Fα(a-1),ab(n-1),Fα(b-1,ab(n-1)),Fα((a-1)(b-1),ab(n-1))。

通过与已求得的F1,F2,F3对比后得出拒绝域，从而得出倾角以及软分层厚度对实验的重要性以及因素间的交互作用对实验的影响。

如果F1≥Fα(a-1),ab(n-1),则拒绝HA0,倾角有显著影响。

如果F2≥Fα(b-1,ab(n-1)),则拒绝HB0,软分层有显著影响。

如果F3≥Fα((a-1)(b-1),ab(n-1)),则拒绝HAB0,倾角与软分层交互作用有显著影响。

4 结 论

(1) 通过层次分析法分析计算得出，对于贵州盘县金佳矿来说，地质构造是造成煤与瓦斯突出的重要原因，为该矿瓦斯防治提供方向，具有一定参考意义。

(2) 运用方差分析法来检验层次分析法得出的结果，并给出方差分析法分析结果判断依据：如果F1≥Fα(a-1),ab(n-1),则拒绝HA0,因素A有显著影响；如果F2≥Fα(b-1,ab(n-1)),则拒绝HB0,因素B有显著影响；如果F3≥Fα((a-1)(b-1),ab(n-1)),则拒绝HAB0,因素A×B有显著影响。

参考文献：

[1]窦林名，高明仕，张 农.巷道围岩的强弱强结构效应及防冲机理探讨[A].2008全国冲击地压研讨会论文集[C]//徐州:中国矿业大学出版社，2008．

[2]梁家辉,王 凯,田 进,等.基于模糊数学法的煤与瓦斯突出危险性预测[J].华北科技学院学报,2017,14(01):40-43.

[3]李成武,许延超.煤与瓦斯突出主要影响因素主成分分析[J].煤矿安全,2007,38(07):14-18.

[4]王莲芬，许树柏.层次分析法引论[M].北京：中国人民大学出版社,1990:2-9.

[5]孙宏才，田 平，王莲芬.网络层次分析法[M].北京：国防工业出版社,2011:6-10.

[6]范金志,郭德勇,张建国.层次分析法确定煤与瓦斯突出影响因素的权重[J].矿业安全与环保,2004,31(3):4-5,8.

[7]陈治宏,卢国明,吴晓华等.基于AHP的群决策风险评估方法[J].计算机应用,2009,29(S1):125-127，145.

[8]徐 坤,牟春友.运用方差分析法分析白城市月亮湖水库水质[J].中国环境监测,2009,25(02):67-68.