巧用中心对称解决问题

袁 勇

对于图形的中心对称性，许多同学虽然能掌握，但并不能灵活运用.本文通过一些例子来说明平行四边形的中心对称性在几何题中的应用.

一、旋转对称的性质

【例1】如图1所示，在正方形ABCD中，E、F分别是AD、CD中点，CE、BF相交于点M，请你说明AM和AB的关系.

图1

【分析】要确定AB和AM的关系，只要将△EDC绕点E旋转180°到△EAN的位置，并说明△MNB为直角三角形且MA为其斜边中线即可.

【解】∵E为AD中点，在正方形ABCD中，∠D=∠BAD=90°，∴将Rt△EDC绕点E 旋转 180°后得Rt△EAN，则Rt△EDC≌Rt△EAN.∴AN=CD=AB.∴A为NB中点.又∵F是CD中点，∴DF=CF,∠D=∠BCD=90°，BC=CD.∴ Rt△ EDC≌Rt△ FCB，∴∠CBF=∠DCE.又∵∠CBF+∠MFC=90°，∴∠DCE+∠MFC=90°.∴∠FMC=90°，即△NMB为直角三角形.∵A是NB中点，∴AM=AB.

二、中心对称图形的性质

【例2】如图2所示，在梯形ABCD中，DC∥AB，M、N分别为对角线AC和BD的中点（.1）判断MN、AB、DC的位置关系；（2）简述MN=（AB-DC）的理由.

图2

【分析】解决中点问题，常利用中点作中心对称图形，进而构造全等三角形.

【解】（1）连接CN并延长，交AB于点E.∵N为BD 中 点 ，∴DN=BN，∠DNC=∠ENB.∵DC∥AB，∴∠1=∠2.∴△DCN≌△BEN.∴CN=EN，DC=BE.在△CAE中，CN=EN，CM=AM，∴MN∥AB.（2）∵AE=

三、平行四边形的中心对称性

【例3】过▱ABCD对角线AC、BD的交点O作两条相互垂直的直线EF、GH，分别与▱ABCD四条边交于E、F和G、H，如图3所示.试判断四边形EGFH的形状，简述理由.

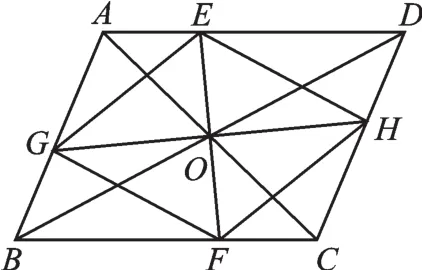
图3

【分析】由题意可知，四边形EGFH首先为平行四边形，又因为EF⊥GH，故为菱形.

【解】四边形EGFH是菱形，理由是：∵四边形ABCD的对角线AC、BD交于点O，∴O是ABCD的对称中心.∵GH过点O，交CD于H点，交AB于点G，∴G、H是以O为对称中心的对称点.∴OG=OH.同理OE=OF，∴四边形EGFH为平行四边形.又∵EF⊥GH，∴▱EGFH为菱形.

以上几例是最为常见的几种对称变换，具有一定的代表性.“对称变换，变而不变”，所谓变，是因为把某个图形或其某一部分转换到了一个新的位置；所谓不变，是指在变化中，被转化部分的内部结构未变，而且与其他对象的内在关系未变.