机床热误差神经网络建模对比实验研究

刘 康，余 玲，杨大志

（四川理工学院机械工程学院，四川 自贡 643000）

引言

目前，减小机床热误差的方法主要有两种：误差防止法和误差补偿法。在误差补偿法中，影响补偿精度和性能的主要因素为热误差模型［1］。近年来，几种用于热误差模型构建的主要方法包括基于多元回归分析、基于灰色系统、基于时间序列分析，以及基于人工神经网络的建模等［2-6］。鉴于机床热误差影响因素的复杂性和非线性特征与人工神经网络建模的特点比较吻合，因此，基于人工神经网络的机床热误差建模得到了较为广泛的应用［7-10］。但各种方法用于热误差模型有何特点，有必要对其进行更多的研究。针对这一问题，本文在同一机床的相同测试数据基础上，采用几种常用的人工神经网络进行热误差建模，从而进行比较性研究。

1 实验方案及关键温度点选择

对一台立式加工中心KVC650E的主轴轴向热误差进行相应的测试实验，以获取有对比研究价值的实际数据。测量包括主轴电机、主轴上轴承、主轴下轴承、主轴中部、环境温度、以及主轴的轴向误差。为了考察不同的环境影响，在不同时间进行了多次测量，见表1。

表1 实验测量数据

在热误差模型构建中，对于多个温度点，如何确定合适的用于模型构建的温度点是需要仔细考虑的。不失一般性，采用模糊聚类法对温度测点进行分类，再根据温度与误差之间的灰色综合关联度确定关键温度点。

表2是对1＃实验数据的8个温度测点进行模糊聚类分类的结果，其中，T1为主轴顶部，T2为主轴电机，T3、T6为主轴上轴承的侧面和正面，T4为主轴下轴承，T5、T7为主轴中部的侧面和正面，T8为环境温度。表3是对1＃实验数据的温度变量与轴向热误差灰色综合系数排序结果。

表2 温度测点模糊聚类分类结果

表3 温度变量与轴向热误差灰色综合关联系数

根据模糊聚类结果，可以在每类中选择一个代表温度点。在表3给出的关联系数中，选择每类中最大的一个作为代表温度点，即为 T1、T2、T6、T8。由表3可知，T1的关联系数最小，不应该选择，故选择T2、T6、T8（主轴电机、主轴上轴承、环境温度）作为温度关键点。另外，T4的主轴下轴承的关联系数也很大，事实上，上下轴承也是主轴主要热源，因此，最终选择主轴电机、主轴上下轴承、环境温度四个关键温度点。为网络输出，从而构建出网络热误差模型。

BP网络和级联网络隐含层选取节点数为2，神经元函数为隐含的正切S型函数1。输出层神

2 模型建立与对比

2.1 几种神经网络热误差模型建立

基于Matlab工具箱，选择热误差模型建模中常用的BP网络newff、级联神经网络newcf、径向基网络newrb、广义回归神经网络newgrnn进行对比建模研究。

本文选择的四个关键温度点中，环境温度作为对不同时间和季节环境的关键温度，可以作为模型的一个独立输入，也可以将其他温度减去环境温度。不失一般性，为了更好地标定不同时间环境的特点，采用其他温度减去环境温度的增量温度，这样，获得了三个增量温度。将增量温度作为网络输入，而将主轴轴向热误差作经元函数为线性函数y＝x。网络训练采用Levenberg－Marquardt学习规则。

径向基网络在构造时可以调整的参数有两个，一个是训练的均方差，一个是平滑参数。广义回归神经网络的平滑参数是构造时能够设置的唯一参数，采用均方差法来确定该参数。

2.2 自预测性能实验

自预测性能是将实测数据用来进行网络训练建模，训练结束建模完成后，将模型用于训练数据自身的热误差预测，考察预测效果与实际测量误差的准确性。为了较准确地考察预测性能，采用两种方式进行：（1）将一组实验数据全部用于网络训练建模，然后再对该组数据进行预测验证；（2）将一组实验数据按照1、3、5……点和2、4、6……点进行抽点后分为新的两组，第一组用于训练建模，第二组用于预测验证。网络构造和训练时的相关参数见表4与表5。

表4 BP网络和级联网络构造训练参数

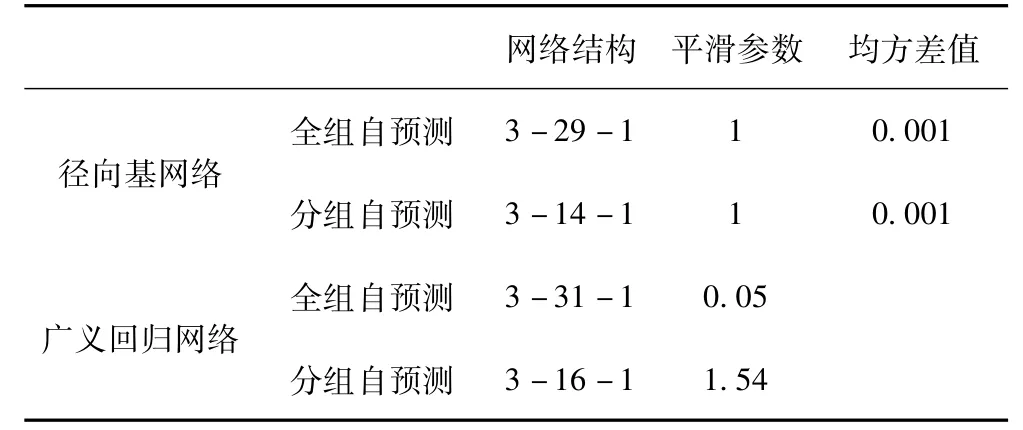
表5 径向基网络和广义回归网络构造训练参数

图1和图2是BP网络和径向基网络对1＃数据进行全组和分组自预测的结果。其中图1（a）与图2（a）为全组自预测结果，图1（b）与图2（b）为分组的自预测结果。1＃数据的全组和分组自预测对比研究结果见表6。

图1 1＃数据BP网络预测结果

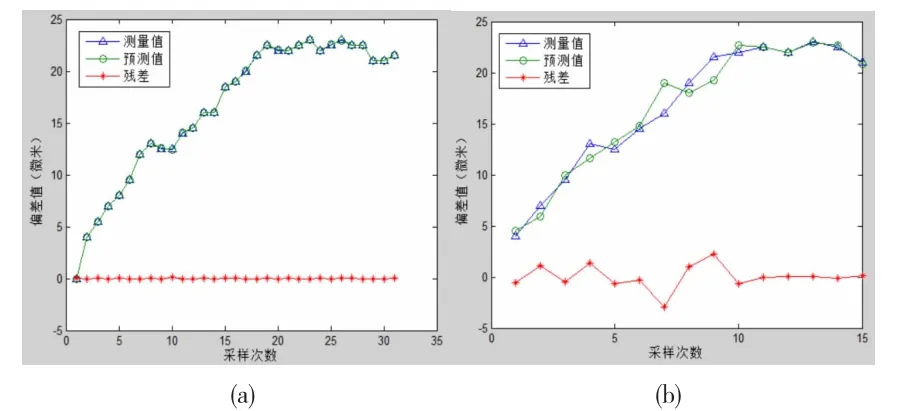
图2 1＃数据径向基网络预测结果

表6 各网络1＃数据自预测残差与均方差

由表6可知，四种网络建立的模型对于自预测都能获得可以接受的结果。特别对于全组自预测，由于是对训练数据本身的预测，其预测效果更佳。径向基网络和广义回归神经网络由于其本身就具有更好的回归和拟合效果，所以其全组自预测获得了较为满意的效果。分组自预测由于其训练数据和测试数据不是相同数据，所以其预测效果比全组自预测而言有所下降，但都在可接受的范围。相比而言，BP网络和级联网络的效果下降程度比径向基网络和广义回归网络要小，表明BP网络可能具有更佳的推广能力。分组自预测的测试方式从某种程度上反映了各模型一定的推广能力。但这种推广能力由于其测试数据依然与训练数据是同一组数据，其内部的特征、模式等特点是一致的，仅仅依靠分组自预测的方式考察模型的推广能力，并将其用于模型构建是不够的。

2.3 推广性能实验

为了更好地考察各网络建模的推广能力，根据实际情况进行了推广性能实验。采用全组1＃数据进行网络训练和建模，将建立的模型用于2＃～5＃数据的热误差预测。图 3是 BP网络模型对 2＃、3＃、4＃、5＃数据推广预测结果。所有网络对应的最大残差绝对值和均方差见表7。

图3 BP网对2＃、3＃、4＃数据预测结果

由图3可知，采用目前常用的简单整体建模方式，模型的推广性能较差。即便相对效果稍好的BP网络，对于4＃数据的预测最大残差也达到了12μm，偏离整个测量数据近50%。而对于拟合能力较强的径向基网络和广义回归网络，基本不具备任何推广能力。

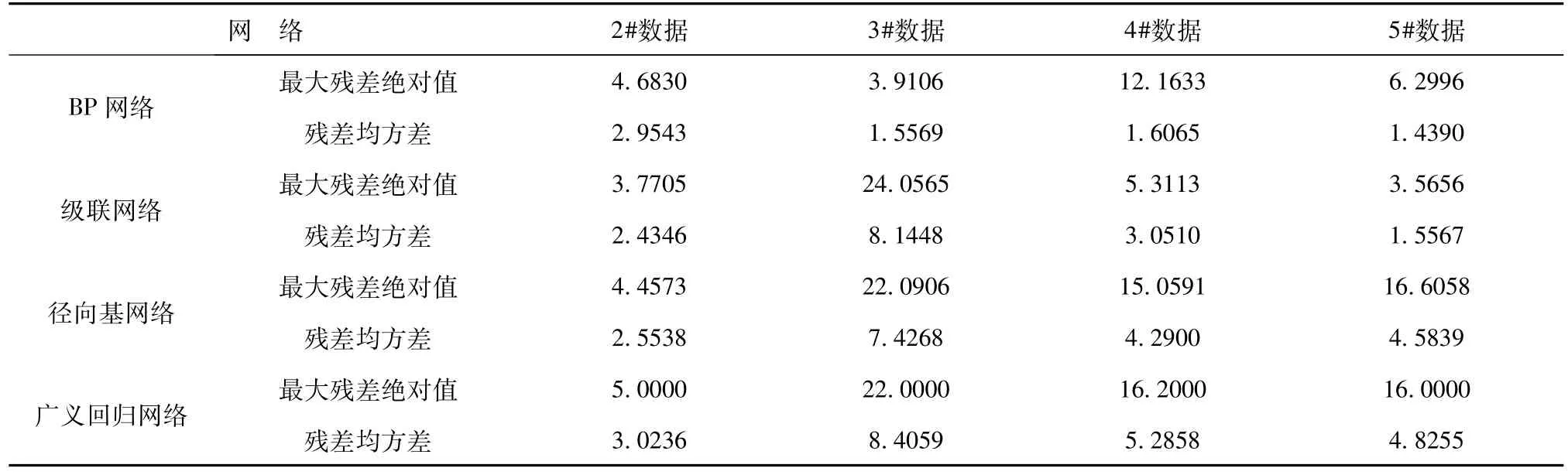
表7 各网络模型对2＃、3＃、4＃、5＃数据预测的最大残差和均方差

3 结果分析

主轴的热误差来源主要是主轴温度变化导致的热膨胀产生的，故其变化过程主要受主轴热源的传入热量和主轴向环境散热影响，呈现从机床开机开始逐渐升高至热平衡的趋势。其他如环境变化等各种因素的影响，使其温升和热误差变化过程呈现了非线性、多因素的复杂特征。随时间变化的热误差E（t）可以由下式表征：

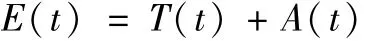
式中，T（t）为由于温度变化引起的误差，A（t）为由其他因素引起的误差。若假设T（t）为一与温升正比的光滑曲线，将5组样本抽点统一到相同时间尺度，采用 fit（X，Y，’poly2’）对误差数据进行二次多项式拟合，结果见表8。

表8 各样本拟合结果及与原始误差均方差

由表8可知，拟合曲线与原始误差均方差都接近1，表明实际误差围绕拟合曲线的波动占了相当比例，这种波动可以认为主要由非温升的其他随机因素，即A（t）引起。传统的神经网络热误差补偿的误差模型大多建立在基于多个关键温度点输入从而获得相应热误差预测值的整体建模方法上，基本思想是希望利用神经网络良好的非线性和学习特性，通过训练，自行寻找出符合热误差规律的模型。从上述分析可以知，如果神经网络能够寻找出T（t）函数关系，再寻找出A（t）函数关系，最后综合获得模型，就可以具有较好的预测精度以及较强的鲁棒性［11-12］。

BP网络学习结果实际是调节网络各权值和偏置，使其所有输出获得的输入与样本输出误差小于预定值，这可以看作是高度逼近样本的非线性拟合。要想在拟合过程中单独抽取T（t）和A（t），是没有理论和方法上的保障的。特别由于A（t）的随机性以及BP网络学习的随机性，基本不可能抽取出整合两种因素的良好函数特征。

同样，广义回归神经网络实际上比BP网络具有更佳的拟合性能，但从前面的讨论可知，其更不容易分别抽取T（t）和A（t）的特征。从本文实验结果可知，BP网络和级联网络基本不具备推广能力，而广义回归神经网络和径向基网络则比BP网络具有更差的推广性能。

其实神经网络的泛化能力，一直是有关学者研究的焦点之一［13-15］。目前的结果表明，影响神经网络泛化问题的众多因素中，网络结构的复杂性和样本的复杂性起着重要作用。在网络结构方面，对于给定一组训练样本，相同样本复杂性最小的结构具有最好的泛化能力是一个基本原则。即达到相同训练精度的网络中，结构越简单，泛化能力越好。在样本复杂性方面，主要体现在样本质量和样本规模两个方面。如果样本分布越能体现总体的真实分布，则样本质量越好。此外，网络学习的影响体现为两个阶段，初始阶段随着学习精度的提高，其泛化能力有所提升，但学习精度的进一步提高，则可能进入泛化能力下降的阶段，亦即过拟合现象发生［16-17］。

考虑热误差补偿的实际情况，一个可用的较好方案是在相应机床出厂前作一个简单的数据采集，并将采集数据用于该机床热误差模型的相应参数。但这样的做法只能够收集有限样本，同时，样本中也不可能包含不同环境、不同时间段和各种工况的信息。这样的样本分布不可能体现总体的真实分布，属于小样本、贫信息。所以从样本复杂性上提升热误差模型的推广能力是不太现实的。而网络结构方面，目前还没有更好的办法。采用简单的整体建模的神经网络，对于构建具有可实用推广能力的热误差模型具有很大的难度。同样仅仅调整学习精度，采用提前终止学习等常规提高泛化能力方法对于构建实用的热误差模型还具有较大差距，因此，必须进行更多的研究，采用其他方法才有望能较好地解决目前的推广能力问题。

参考文献：

[1]王海同,李铁民,王立平,等.机床热误差建模研究综述[J].机械工程学报,2015,51(9):119-128.

[2]张毅,杨建国.基于灰色理论预处理的神经网络机床热误差建模[J].机械工程学报,2011,47(7):134-139.

[3]姜辉,杨建国,李自汉,等.基于误差分解的数控机床热误差叠加预测模型及实时补偿应用[J].上海交通大学学报,2013,47(5):744-749.

[4]KANG Y,CHANG C W,HUANG Y,et al.Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools[J].International Journal of Machine Tools&Manufacture,2007,47(2):376-387.

[5]ESKANDARI S,AREZOO B,ABDULLAH A.Positional,geometrical,and thermal errors compensation by tool path modification using three methods of regression,neural networks,and fuzzy logic[J].International Journal of Advanced Manufacturing Technology,2013,65(9-12):1635-1649.

[6]刘志峰,潘明辉,张爱平,等.基于灰色线性回归组合模型的机床热误差建模方法[J].高技术通讯,2013,23(6):631-635.

[7]马驰,杨军,梅雪松,等.基于遗传算法及BP网络的主轴热误差建模[J].计算机集成制造系统,2015,21(10):2627-2636.

[8]李逢春,王海同,李铁民.重型数控机床热误差建模及预测方法的研究[J].机械工程学报,2016,52(11):154-160.

[9]张景然,沈牧文,杨建国.基于模拟退火遗传算法优化BP网络的数控机床温度布点优化及热误差建模[J].机床与液压,2014(23):1-4.

[10]马驰,赵亮,梅雪松,等.基于粒子群算法与BP网络的机床主轴热误差建模[J].上海交通大学学报,2016,50(5):686-695.

[11]余文利,姚鑫骅,孙磊,等.基于 PLS和改进 CVR的数控机床热误差建模[J].农业机械学报,2015,46(2):357-364.

[12]郭前建,徐汝锋,贺磊,等.基于逐步回归的机床温度测点优化及热误差建模技术[J].制造技术与机床,2015(12):89-92.

[13]王恺,杨巨峰,王立,等.人工神经网络泛化问题研究综述[J].计算机应用研究,2008,25(12):3525-3529.

[14]赵远东,胡为尧.人工神经网络泛化性能改进[J].南京信息工程大学学报:自然科学版,2011,3(2):164-167.

[15]郑素娟,黄美发,张奎奎,等.多工况下数控机床主轴热误差建模[J].组合机床与自动化加工技术,2017(7):27-31.

[16]郭前建,王红梅,李爱军.机床热误差建模技术研究进展[J].河北科技大学学报,2015,36(4):344-350.

[17]李泳耀,丛明,廖忠情,等.机床热误差建模技术研究及试验验证[J].组合机床与自动化加工技术,2016(1):63-66.