基于CFD的直线型导流罩加速性能研究
2018-05-22邓智雯袁军亭王世明王立原
邓智雯, 袁军亭, 王世明, 王立原
(上海海洋大学 工程学院, 上海 201306)
1 研究背景
随着化石能源的紧缺及全球气候变暖,清洁、可再生能源的开发与利用日益受到世界各国的关注,对改善能源结构具有战略作用。海洋能不仅是清洁能源,同时也是可再生自然能源,一般包括波浪能、潮汐能、潮流能、盐差能、温差能等。我国海洋能资源丰富,海洋能发电技术的研究也正在逐步发展。但由于海域流速及波浪的不规则性等因素,致使我国现有的海洋能发电装置发电功率较小、可产生发电工作的时间短、发电机组结构尺寸过大、开发成本较高等问题[1]。
加拿大的Faure等[2]在1986年提出可以在垂直水轮机结构外部加装导流罩。随后,阿根廷的ISEP小组再次提出在垂直水轮机外加装导流罩方法,并研究了导流罩对垂直水轮机的发电效率影响。研究结果表明加装导流罩能使叶轮附近流域的流速增大,能提高发电效率,由此可以达到减小发电机组尺寸,节约成本的目的[3]。随着数值模拟仿真技术的应用和发展,王树杰等[4]对4种不同母线的导流罩进行了数值模拟,初步分析了开口张角对圆形导流罩的水动力性能影响。王俊皓等[5]采用数值模拟的方法,对变角度导流罩进行了水动力设计。
本文采用数值模拟与实验设计相结合的方法,对不同结构参数下的直线型导流罩进行了数值模拟的正交实验。通过实验,探索其主要结构参数对直线型导流罩的加速性能的影响规律,找到影响其加速性能的主要因素,最终的得出较优的方案组合。
2 导流罩结构与原理
2.1 导流罩特征与工作原理
直线型导流罩如图1所示分为扩口段和中间段。扩口段直径与中间段的直径的差值,使得流体经过导流罩的时候,产生高低压差,从而产生抽吸作用,从而使得流体经过中间段的时候流速得到加速[6-7],将此性能称作为加速性能,显然导流罩中部流速相对于来流流速越大,加速性能越优,所以本研究中将以导流罩中部的流速与水流入口处的流速的比值作为衡量指标。

图1 导流罩示意图
2.2 加装导流罩对轴流式浪流发电装置水轮机的影响
波浪能发电装置是通过波浪带动水轮机旋转,经过能量转换装置将水轮机输出轴的机械能转化为电能。而导流罩加装在水轮机之外(如图1所示),可增加作用在水轮机上的水流速度。根据贝兹理论,水轮机的输出轴功率计算公式[8]可简写为:
(1)
式中:P为输出功率,W;ρ为液体密度,kg/m3;S为迎流面积,m2;v为来流速度,m/s;Cp为功率系数。
由上式可知,功率与流速3次函数关系,当流速增加,水轮机的输出轴功率将大大增加。因此提高导流罩的加速性能,对提高发电机的发电功率有显著的效果。
3 正交试验
3.1 水力设计
导流罩的加速性能主要取决于导流罩的结构尺寸。直线型导流罩结构尺寸主要参数包括扩口段直径D、中间段直径d、扩口段长度L、中间段长度H和开口张角α。如图2所示:
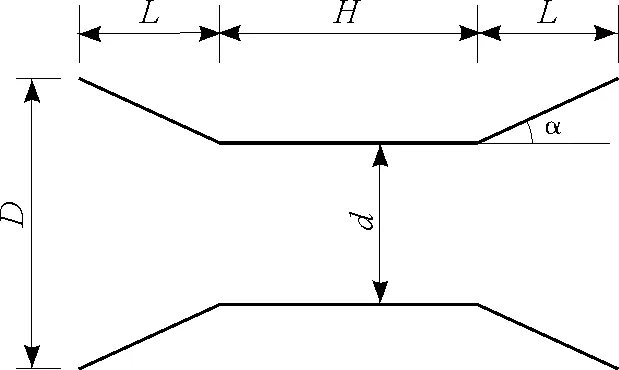
图2 导流罩结构参数示意图
本研究中,直线型导流罩的是装在直径为500 mm的叶轮之外,先将导流罩中间段直径定为600 mm。设定无穷远处的水流速度为3 m/s,方向与导流罩入口垂直,根据正交试验要求设计出9种直线型导流罩,通过CFD仿真,找出其加速性能较优的方案。
3.2 试验因子与试验方案

由于导流罩的结构受到叶轮结构以及装配在叶轮两段的发电机长度大小的影响,同时为了整个浪流发电机的协调构造,导流罩总长度不得超过3 000 mm,中间段长度H不得低于600 mm。因流体在流动过程中,流体之间的相对运动会产生切应力以及流体与固壁之间不可避免的产生摩擦阻力[9]。若中间段过长则会增加流动阻力,从而产生不必要的能量损失,同时也会导致扩口段长度过小,从而产生迎流面积过小、增速效果显著减弱等不利影响。开口张角α的大小影响着导流罩引流面积的大小以及导流罩的扩口段局部阻力[9]。故根据经验将L的实验参数定为400,700,1 000 mm,H的试验参数定为600,800,1 000 mm,α的实验参数定为15°,25°,35°。因子水平如表1所示。

表1 导流罩因子水平表
根据标准的正交表,选用L9(34)正交表,由因素水平表及正交表得出表2所示的9种结构参数配置的试验方案。通过试验可以得出扩口段长度L、中间段长度H和开口张角ɑ对直线型导流罩的加速性能的影响规律。

表2 试验方案
4 导流罩数值模拟仿真
利用流体仿真软件,可以进行对不同结构参数的导流罩进行仿真试验,可得出指定位置随着时间的流速的变化情况。
4.1 模型的选择
本研究模型采用Standardk-ε模型湍流模型,运用Segregated隐式求解器,压力和速度耦合采用Couple算法。湍流动能方程、动量方程以及耗散率方程采用二阶迎风格式,为了让计算结果更快的收敛,采用欠松弛技术,特殊耗散率、湍动能松弛因子、松弛因子、速度欠松弛因子均取 0.3, 其他默认。残差收敛均取为0.0001。
Standardk-ε的数学表达式如下,详细推导过程可参考文献[10]。
其湍动能方程为:
Gk+Gb-ρε-YM+Sk
(2)
湍动能耗散率方程为:
(3)
式中:k为湍动能,J;ε为湍动能耗散率;ρ为液体密度,kg/m3;ui为速度,m/s;Gk为平均速度梯度所导致的湍动能,J;Gb为浮力所导致的湍动能,J;YM为可压缩湍流波动扩张对整体耗散率的贡献;σk为湍动能普特朗常数;σε为湍动能耗散率普特朗常数;Sk、Sε为用户自定义的湍动能和湍动能耗散率的源项;μt为湍黏性系数;C1ε、C2ε、C3ε为常数。
4.2 网格划分与边界条件
在Gambit中,建立导流罩的二维平面模型,因导流罩为轴对称模型,故采用二维轴对称模型来提高计算速度[11-15]。整个计算域以轴线的中心点为坐标原点,以过导流罩轴线的中点并垂直于轴线的直线为基线,以入口距离基线3D(D为导流罩扩口段直径),出口距基线5D,保证计算域内流体充分发展[11-12],并根据模型划分合适的网格。结构网格能够节省大量的内存空间,拥有更高的计算效率,本文采用分块网格技术进行结构网格划分。网格划分结果如图3所示,将接近导流罩壁面及其内部的网格细化。
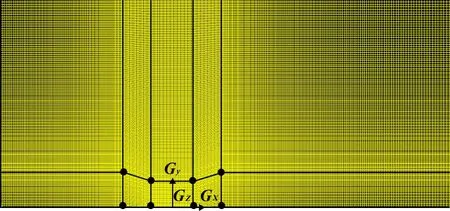
图3 网格划分
此模型边界条件,参照中国海洋大学工程学院的王树杰等[4]的模型,入口为速度入口,假定来流来自于无穷远处,且速度为匀速3 m/s,方向垂直于导流罩入口;出口为自由出口,流域的上边界和导流罩边界为无滑移壁面,对称轴所在边界为对称边界。
5 仿真数值模拟与模型试验结果分析
5.1 仿真结果
数值计算9组方案的得到速比值如表3所示。

表3 试验结果
从表3中可以看出,A3B2C1为导流罩转化速比最大。为排除随机因素,验证各结构参数对中间段流速,轴向力系数影响的主次顺序,需要对表3中的数据作极差分析。极差分析方案如表4所示:
由表4可知,A3B2C1方案为导流罩转化速比最大,且极差关系为:RA>RC>RB,因此结构参数对导流罩转化速比的影响顺序为:扩口段长度>开口张角>中间段长度。
综上所述,方案8导流罩加速性能最佳。如图4所示:由导流罩入口处沿轴线,水流速度呈阶梯式增加,在导流罩中部产生的明显的增速效果。沿轴线方向的速度曲线如图5所示,速度在中间位置达到了最大值6.4 m/s。相对于最差的方案速比提高了42.83%。

表4 极差分析表

图4 方案8导流罩仿真结果图
5.2 模型试验
得到最佳转化速比的导流罩后制作模型。在上海东海计量中心水槽中进行了试验,试验装置如图6所示。试验装置为方案8中的导流罩模型,海流计等。
一共进行了10组试验。试验过程中,将导流罩安装在支撑结构上,将海流计固定在导流罩的轴线上不同的10个位置(如图7所示),设计拖曳速度为3 m/s,分别进行10次试验。通过海流计测得导流罩轴线不同位置处的流场速度,将试验结果与仿真结果绘制在同一个图中,如图8所示。

图5 方案8导流罩沿轴线的速度

图6 试验装置图
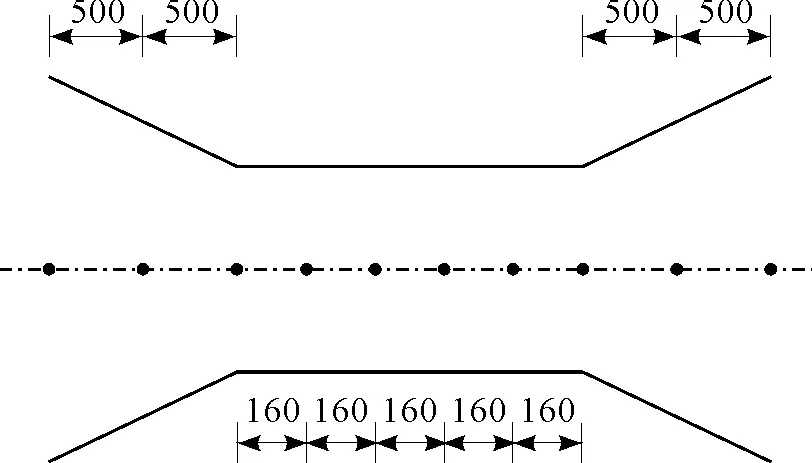
图7 导流罩水槽试验流速测量点
由图8可知,在导流罩迎流方向扩口段,流场速度迅速增加,从3.1 m/s左右迅速增加至5.5 m/s,在中间段流场速度达到最大6.0 m/s左右,中间段过后又开始不断减小至3.4 m/s左右。在入口及出口段速度较仿真低一些,这是由于水流冲击导流罩,出现微小的能量损失。试验结果与仿真结果符合较好,趋势基本一致。

图8 水槽试验导流罩轴线流速
6 结 论
(1)本文采用正交试验,通过改变直线型导流罩的结构参数来分析其结构参数对导流罩加速性能的影响,探究表明不同结构参数组合下,导流罩的加速性能明显不同。
(2)试验结果分析表明,导流罩扩口段长度和开口张角是影响加速性能的主要因素,中间段张都对加速性能影响不大。
(3)通过对正交试验结果作极差分析,得到导流罩结构参数的对其加速性能的影响的主次顺序。大大缩短了优化导流罩的时间,为轴流式浪流发电机的导流罩设计提供了依据。
参考文献:
[1] LI Dong ,WANG Shujie ,YUAN Peng .An overview development of tidal current in China: Energy resource, conversion technology and opportunities[J].Renewable and Sustainable Energy Reriews,2010,14(9):2896-2905.
[2] FAURE T, PRATTE B SWAN D. The darrieus hydraulic turbine-model and field experiments[J].Asme Int Hydro & Power Fluid Machinery Symposium Anaheim California Usa, 1986,43:123-129.
[3] PONTA F L,JACOVKIS P M. A vortex model for darrieus turbine using finite element techniques [J].Renewable Energy,2001,24(1):1-18.
[4] 王树杰, 徐世强,袁 鹏,等.轴流式潮流能发电装置导流罩水动力特性研究[J].太阳能学报,2014,35(6):1098-1104.
[5] 王俊皓,李国富,徐晓倩,等.一种变角度导流装置的水动力设计[J].水资源与水工程学报,2015,26(3):197-201.
[6] 王俊皓.小型海浪发电系统变角度导流装置及其性能分析[D].宁波:宁波大学,2014.
[7] 孙桂林.导流型潮流发电水轮机关键部件有限元分析[D].哈尔滨:哈尔滨工程大学,2012.
[8] LANCHESTER F W. A contribution to the theory of propulsion and the screw propeller[J].Journal of the American Society for Naval Engineers,2010,27(2):509-510.
[9] 王 亮. 流体力学与流体机械[M].长春:吉林大学出版社,2016,89-104.
[10] 王福军,计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2006:120-123.
[11] 张亮,孙 科,罗庆杰.潮流水轮机导流罩的水动力设计[J].哈尔滨工程大学学报,2007,28(7):734-737.
[12] 陈存福, 王树杰, 袁 鹏,等. 潮流能水平轴水轮机导流罩水动力学特性数值分析[C]// 中国可再生能源学会2011年学术年会论文集,北京:中国可再生能源学会, 2011.
[13] 荆丰梅,张 亮,张鹏远,等. 潮流能发电增速导流罩研究[J].哈尔滨工程大学学报,2012,33(4):409-413.
[14] 汪鲁兵. 竖轴潮流水轮机水动力性能理论与实验研究[D]. 哈尔滨:哈尔滨工程大学,2006.
[15] 高 智. 壁判据用于计算流体力学(CFD)可信度评估[J].空气动力学学报,2008,26(3):378-383+393.
